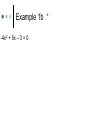* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 5.6 – Quadratic Equations and Complex Numbers
Location arithmetic wikipedia , lookup
Positional notation wikipedia , lookup
Recurrence relation wikipedia , lookup
Large numbers wikipedia , lookup
Hyperreal number wikipedia , lookup
Factorization wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
System of polynomial equations wikipedia , lookup
Elementary algebra wikipedia , lookup
5.6 – Quadratic Equations and Complex Numbers Objectives: Classify and find all roots of a quadratic equation. Graph and perform operations on complex numbers. Standard: 2.5.11.C. Present mathematical procedures and results clearly, systematically, succinctly and correctly. Discriminant The expression b2– 4ac is called the discriminant of a quadratic equation. If b2– 4ac > 0 (positive), the formula will give two different answers. If b2– 4ac = 0, there will be one answer, called a double root. If b2– 4ac < 0 (negative), the formula gives no real solutions Ex 1. Find the discriminant for each equation. Then determine the number of real solutions for each equation by using the discriminant. Imaginary Numbers If r > 0, then the imaginary number follows: r = 1 r = i r Example 1a r is defined as Example 1b * -4x2 + 5x – 3 = 0 Example 1c * 6x2 – 3x + 1 = 0 Complex Numbers Example 1a and b* b. 2x + 3iy = -8 + 10i Operations with Complex Numbers c. (-10 – 6i) + (8 – i) (-10 + 8) + (-6i – i) -2 – 7i Multiply (Example 2) b. (6 – 4i)(5 – 4i) FOIL c. (2 – i)(-3 – 4i) FOIL Conjugate of a Complex Number The conjugate of a complex number a + bi is a – bi. To simplify a quotient with an imaginary number in the denominator, multiply by a fraction equal to 1, using the conjugate of the denominator. This process is called rationalizing the denominator. Example 1a 2 5i 2 3i 2 5i 2 3i Next step : FOIL 2 3i 2 3i Example 1b 3 4i 2i 3 4i 2 i 2i 2i Writing Questions