Download Jan31

Jan. 31, 2011
Einstein Coefficients
Scattering
E&M Review:
units
Coulomb Force
Poynting vector
Maxwell’s Equations
Plane Waves
Polarization
Calculate αν and jν from the Einstein coefficients
Consider emission: the emitted energy is


dE
(
)

dV
d

d
dt (1)
j
where

em
coeff
t,
ergs
issi
/ste
j






d

frequ
elem
dV

volume
elemen
d


solid
angle
elemen
dt

time
eleme
(
)

prob
y
em
oc
pe
th
se
A
21
(
)

#
of
emi
ev
se
/
n
A
21
2
Each emission event produces energy hν0
spread over 4π steradians
so
 



h


0
(2)
dE
(
)

(
)
dV
d

d
dt

n
A
21
2
4


From (1) and (2):
h



0


(

)
j
n
A
 

4

2
21
Emission coefficient
Absorption coefficient:
Total energy absorbed in
In volume dV is



(
,

d
)
and
(
t
,
t

dt
)





1
dV
dt
dh
n
B
d

d(
)
I
0 1
12



4













energy
per
absorption
#
absorption
s/sec
or
Let

 

h
0
dE

dV
dt
d
n
B
d

1
12 I

4



dI
dA
dt
d

d
Recall: dE
dV

dA
ds


h

dE

dAds
dt
d
n
B 
I

d
4

h


B

(

)
 n

(

I
ds
)
dA
dt
d

d



4

dI


I
ds



so
0
112
0
11 2
Stimulated Emission
Repeat as above for absorption, but change sign,
and level 1 for level 2

 


h
0


n
B
()

2
21
4
em
So the “total absorption coefficient” or
the “absorption coefficient corrected for simulated emission” is




h
 (
)
(
n
B

n
B
)

1
1
2
2
1
2
4
Equation of Radiative Transfer


dI



I
j



ds


 

dI
h
h


(
n
B

n
B
)
(
)
I

n
A
(
)
1
1
2
2
2
1

2
2
1



 4
ds
4







ab so rp t io
n
The Source
Function
st imu l at ed
sp
s n t an
emissio
n o
emissio
h
nA
(

)
2 21
4

j

S


h



n

(

)
B

n
B
1
12
2
21
4

n
A
2
21
S


n
B

n
B
1
12
2
21
Recall the Einstein relations,
3
2
h




2
A
B
21
21


c
 B
g
B
12 g
1
2 21




g

h
n
1
2

 n
B
1
 
()

1
12


4
n
2
1
g

g

2
h

n
2
1

S

1
 2 


c g
n
12

3

1
In Thermodynamic Equilibrium:


n
g

h

1
1
 exp
 
n
kT

2 g
2


g

h
n
1
2

 n
B
1
 
()

1
12


4
n
2
1
g

h

h



 n
B
(
1

exp
)
(

)


1
12
4

kT







stimulated
emission
term
And
g

2
h

n
2
1

S

1
 2 


c g
n
1
2

3

1
2h
3

1
h

k T1
 2 exp
c
B

The SOURCE FUNCTION is the PLANCK FUNCTION
in thermodynamic equilibrium
LASERS and MASERS
When
n1 n2

g1 g2


the populations are inverted

 0
g

h
n
1
2

 n
B
1
 
()

1
12


4
n
2
1
g

Since


I

I
(
0
)
exp

ds




I
increases along ray, exponentially
HUGE amplifications
Scattering term
in equation of radiative transfer
Rybicki & Lightman, Section 1.7
Consider the contribution to the emission coefficient from scattered
photons
Assume:
1. Isotropy: scattered radiation is emitted equally in all angles
 jν is independent of direction
2. Coherent (elastic) scattering: photons don’t change energy
ν(scattered) = ν(incident)
3. Define scattering coefficient:
scattering
Incident
mean
intensity
j14
 2 43  
{
Emission
coefficient
scattering
coefficient
}
J


scatteri n
scatteri ng
1
4
S

Scattering source function
j



J

I
d







flux
scattered
flux
scattered







d
I






into
beam
out
of
beam





J
d


s
I
ds




dI
   (I  J )
ds

   I 
1
4
 dI 
An integro-differential equation: Hard to solve.
You need to know Iν to derive Jν to get dIν/ds
Review of E&M
Rybicki & Lightman, Chapter 2
Qualitative Picture:
The Laws of Electromagnetism
• Electric charges act as sources for generating electric fields. In turn,
electric fields exert forces that accelerate electric charges
• Moving electric charges constitute electric currents. Electric currents act
as sources for generating magnetic fields. In turn, magnetic fields exert
forces that deflect moving electric charges.
• Time-varying electric fields can induce magnetic fields; similarly timevarying magnetic fields can induce electric fields. Light consists of timevarying electric and magnetic fields that propagate as a wave with a
constant speed in a vacuum.
• Light interacts with matter by accelerating charged particles. In turn,
accelerated charged particles, whatever the cause of the acceleration,
emit electro-magnetic radiation
After Shu
Lorentz Force
A particle of charge q at position
r
With velocity v
Experiences a FORCE
F
v
F

q(
E

B
)
c
E(r,t) = electric field at the location of the charge
B(r,t)
= magnetic field at the location of the charge
Law #3: Time varying E  B
Time varying B  E
Lorenz
Force
v
F

q(
E

B
)
c
More generally, let

V

Volum
current
density
lim
1

j

q
v
 
i
i

V

0

Vi


charge
density
lim
1



q
 
i

V

0

V
i


Force per
Unit volume
1
f

E
 j
B
c
Review Vector Arithmetic
A
vector
Com
of
vecto
pone
:
(A
,
A
,
A
)
x
y
z
A

B
scala
prod
of
A
an
B
A
"
dot"
B
A
A
A
xB
x
yB
y
zB
z
ABcos(
)
A

A

A

A
2
x
2
y
2
z
A


A cos 
B
projection
of
A
in direct
theof
B
multiplied
bylength
the
of
B
(or versa)
vise
Cross product
Is a vector
AB
A  B  A B  A B
A  B  A B  A B
A  B  A B  A B
x
y
z

magni
of
vec

A
B
si
y
z
z
y
z
x
x
z
x
y
y
x
Direction of cross product: Use RIGHT HAND RULE
The
direction
of
A

B
is
per
la
NOTE:
to
both
A
and
B
ˆ
Ex
in
of
bas
pre
ve
i
,̂
j
te
,̂
k
ˆ
ˆ
ˆ
A

B

(
a
b

a
b
)
i

(
a
b

a
b
)
j

(
a
b

a
b
)
k
y
z
z
y
z
x
x
z
x
y
y
x
iˆ
ˆj
kˆ
 ax a y az
bx by bz
ˆ
ˆ ˆ

i
j k


determinan
tof
matrix
a

xa
ya
z


b
b
b
x y z

T

grad
T
Gradient of scalar field T
is a vector with components
T

Tx 
x
T

Ty 
y
T

Tz 
z
A
divergence
ofvector
A
 div
A
Ax Ay Az



x
y
z
scalar


A
curl
A
A vector with components
  A 
Ay
x
  A 
Az
y
z

x
  A 

y
Ax
z

Ax
y

Ay
z

Az
x
THEOREM:
If


A

0
(cu
of
v

0
then
is
a
scala
the
fiel

such
A



tha
THEOREM
I f
A0 (divergenc
eofvector
0)
Then is
there
a vector
Bsuch that
A
B
Aisthe
curl
of
some
vector
B
Laplacian
Operator:


2
2
2
2 


2
2
2

x

y

z

T

2
2
2
2

T
T
T
2
2
2

x

y

z
T is a scalar field
Can also operate on a vector,
Resulting in a vector:

A

(

A
,

A
,

A
)
2
2 2 2
x
y
z
UNITS
• R&L use Gaussian Units
convenient for treating radiation
• Engineers (and the physics GRE) use
MKSA
(coulombs, volts, amperes,etc)
• Mixed CGS
electrostatic quantities: esu
electromagnetic quantities: emu
Units in E&M
We are used to units for e.g. mass, length, time
which are basic: i.e. they are based on the standard Kg in Paris, etc.
In E&M, charge can be defined in different ways, based on different experiments
ELECTROSTATIC: ESU
2
Define charge by Coulomb’s Law:
Then the electric field
E
e
F
(dynes
) ESU
2
r
cm
is defined by
E4ESU

Ch
arg
e
density
in ESU
Fdynes
1
ergcm
2
ML
1 ML
 2
 2
T L T
2
ESU
2
cm
e
F
(dynes
)
r
So the units of charge in ESU can be written in terms of M, L, T:
[eESU]  M1/2 L-3/2 T-1
And the electric field has units of
[E]  M1/2 L-3/2 T-1
The charge of the electron is 4.803x10-10 ESU
In the ELECTROMAGNETIC SYSTEM (or EMU) charge is defined in
terms of the force between two current carrying wires:
Two wires of 1 cm length, each carrying 1 EMU of current
exert a force of 1 DYNE when separated by 1 cm.
j
ds
ds
1
1j
2
2
dF

2
r
Currents produce magnetic field B:

B4

JEMU
current
density
Units of JEMU (current density):
Since
j
ds
ds
1
1j
2
2
dF

2
r
[jEMU] = M1/2 L1/2 T -1
current
[JEMU] = [jEMU] L-2 = M1/2 L-3/2 T-1
So [B]  M1/2 L-1/2 T-1
Recall [E]  M1/2 L-1/2 T-1
So E and B have the same units
EMU vs. ESU
Current density = charge volume density * velocity
So the units of CHARGE in EMU are:
[eEMU] = M1/2 L1/2
Since M1/2 L-3/2 T-1 = [eEMU]/L3 * L/T
Thus,
[eESU
] L

[eEMU
] T
Experimentally,
[eESU]
c
[eEMU
]
So...
we
can write
the
Lorentz
Force
FeESU
EeEMU
vB
For
GAUSSIAN
units,
Eand
Bare
asabove,
convert
charges
and
currents
inEMU
toESU
bydividing
byc.
MAXWELL’S EQUATIONS
Wave Equations
Maxwell’s Equations
Let
Relate
E
,B
,ρ
,ˆ
j
E

Electric
Field
B

magnetic
field
lim
1

Charge density


q
 
i

V

0

V
i


lim
Current density
1

j

q
v
 
i
i

V

0

Vi


D
E
B
H


DIEL
con


Magn
Perm
ty
Maxwell’s Equations
  D  4
 B  0
1 B
 E  c t
Gauss’ Law
No magnetic monopoles
Faraday’s Law
E
from
cha
B
4
1 D
 H 
j 
c
c t
Magnetic
field
from
changing
E
or
curre
? 
?
We will be mostly concerned with Maxwell’s equations
In a vacuum, i.e.



1

Dielectric Media: E-field aligns polar molecules,
Or polarizes and aligns symmetric molecules

:
"
perm
ty
of
ma
"
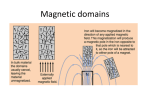
Diamagnetic: μ < 1
alignment weak, opposed to external
field so B decreases
Paramagnetic μ > 1
alignment weak, in direction of field
Ferromagnetic μ >> 1 alignment strong, in direction of external
field