Download L04_Electric_Potential

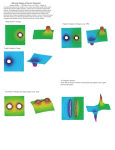
eNERGETICS
So far we have been studying electric forces and fields
acting on charges. This is the dynamics of electricity.
But now we will turn to the energetics of electricity,
gaining new insights and new methods for analyzing
problems—just as we did in classical mechanics in the
first semester.
Electric Potential
This chapter is about “Electric Potential”. We will approach
this topic as follows:
From classical mechanics, a quick review:
1. Kinetic energy, work, and potential energy.
2. Mass-spring system, and conservation of total energy.
3. Gravitational potential energy, UG , near Earth (1D).
Then, on to electricity:
1. Electric potential energy, UE , in uniform E (1D).
2. Introduce electric potential, VE .
3. Find UE and UG in 3D.
4. Solve problems using electric potential.
Kinetic energy, work, and potential energy
Kinetic energy, the energy of motion: K = ½ mv2, for any given mass.
Work, the transfer of energy: force acting through distance:
 
 
W  Fd or W  F  d  Fd cos( ) or W   F  ds   F cos( ) ds

F

d

Potential energy, U. Energy of position: stored in a system as a result
of work. Also known as “pre-integrated work”. Defined only for
conservative systems (those without dissipative forces such as friction).
Calculating potential energy
The “work-energy theorem” states that work done by a system as it
moves an object from a to b changes its potential energy:
Wab  U a  U b  U
Example, spring obeying Hooke’s Law: F = -kx
Wab  U a  U b   (U b  U a )   U
x2
x2
1
1
W   Fdx    kxdx   kx22  kx12  U 2  U1
2
2
x1
x1
U
1 2
kx
2
Energy conservation: Etotal = K + U = ½ mv2 + ½ kx2 = const
Gravitational potential energy near Earth’s surface
The gravitational force field is nearly uniform and pointed downward,
with a constant force: F = -mg
yf
yf
yi
yi
Work-energy theorem  W   Fdy    mgdy  mgy f  mgyi  U f  U i
U = mgy
Since U depends only on y, any
given height is a plane of constant
potential energy: an “equipotential”.
Energy conservation: Etotal = K + U
=
= ½ mv2 + mgy = const
Examples: Inclined planes,
pendulums, roller coasters,
Mt. Lemmon, etc.
Grand Canyon Topo Map
Brown contours
are lines of
constant altitude:
“gravitational
equipotentials”.
Numbers are feet
above sea level.
Where lines are
closely packed
together, the
slope is steep:
the “gradient” is
large.
Gravitational equipotentials at Earth’s surface.
 Discuss slopes (gradients), forces, work, and path independence.
?
B
Find
 Do
A
Saddle points: their contours, and their peculiar
equilibrium points
Electric potential energy in a uniform electric field
The electric force field is uniform (and pointed downward in this
example) with a constant force: F = -qE
Work-energy theorem 
yf
yf
yi
yi
W   Fdy    qEdy  qEy f  qEyi  U f  U i
U = qEy
Since U depends only on y, any
given height is a plane of constant
potential energy: an “equipotential”.
Energy conservation: Etotal = K + U
=
= ½ mv2 + qEy = const
Examples: electron microscope
beams, linear accelerators, …
The electric force is conservative
As in the case of gravity, the work done is path independent.
What, precisely, is “electric potential”???
Electric potential is the electric potential energy per unit charge:
J
Units :    V (volts)
C
UE
VE  V 
q0
So a particle or object with charge q at a location where the electric
potential is V will have a potential energy U = qV. 
Charged plates again, with given voltages:
V 
U qEy

 Ed
q
q

E
U  qV.
600 V
V  V 
d  m 
= .2 m
from which we can find the electric field,
E = (600V – 100V)/(.2 m) = 2500 V/m
100 V
Alessandro Giuseppe Antonio Anastasio Volta
Invented electrophorus
(charging device), the battery
(silver, zinc, and brine),
discovered methane, ignited
gases with electric sparks, …
Volt / meter = Newton/Coulomb
Volta demonstrating his
battery to Napoleone in
1801, by Giuseppe Bertini
1745-1827
V is easily created with batteries or power supplies
A charged capacitor
We can analyze problems with dynamics or energetics
Example: An accelerator/decelerator. (Discuss.)
Dynamics: F = ma
F = qE = ma  a = qE/m
Then, we would do kinematic analysis.
Conservation of total energy: K + U
1 2
1 2
mvi  qVi  mv f  qV f
2
2
This method can be applied to any
system for which we know V !
Two ways to calculate V for new systems
1. As we’ve been doing, start from the work-energy theorem:
 
W  U   F  ds
 
U    F  ds
U
V 
q0
2. Or, notice that if we divide both sides of the middle equation above by
the test charge, we can find V directly from the electric field:

U
F 
    ds
q0
q0
 
V    E  ds
In most cases, we’ll find the second approach more convenient for
finding the electric potential.
Electric potential of a point charge
This result will be the “building block” used to calculate V systems of
point charges or continuous charge distributions:
r
r
kq
kq
kq
dr


 0  Vr  V
2
r
r  r

V   Edr  

r
We have chosen the potential to be
zero at infinity, giving us this very
simple result to carry forward: the
electric potential of a point charge.
kq
V 
r
No vector quantities to
complicate things!
But we also must be aware of the charge sign,
and its effect on V
Path independence again
Since the electric force is
conservative, and the field is
central (along the line of centers
between charges), the work done
on a charge moving between any
two points is independent of the
path taken. This allows for the
definition and calculation of an
electric potential, V.
The many representations of V for a positive charge
kq
V 
r
Electric potential obeys the superposition principle
For any system of point charges
kqi
V  Vi  
ri
i
i
For this system of 3 charges:
kq1 kq2 kq3
V


r1
r2
r3
No vector algebra to fuss with!
But, in general we may need to calculate the distances using:
ri 
x  xi 2   y  yi 2  z  zi 2
Where position a is (x,y,z), and the ith charge is at (xi,yi,zi).
Equipotentials of familiar charge distributions
Equipotentials of a dipole – two representations
 Do
Some potentially interesting examples
Electric potential for continuous charge distributions
We can find V for continuous charge distributions starting from the
equation for a point charge. The method is similar to that used to find
F or E, but without the need for vector quantities in the integrand.
point charge
differential form
integrate to find V
kq
V 
r
kdq
dV 
r
dq
V  k
r
pick dq based on the given charge distribution
3
dq  ds or dq  dA or dq  dr
Turn the crank and the answer will appear…
Electric potential of a uniform ring of charge
We can avoid doing an integration here! How?
Write down the answer “immediately”.
Electric potential of a disk of uniform charge
Apply the same tactic we used for the electric field of a disk: divide the
disk into infinitesimal rings of potential dV, and integrate from 0 to R.
Comparing potentials of point charge and disk charge
 Sketch
Electric potential of a finite line of charge
 Set up
Electric potential of an infinite line or cylinder of charge
This calculation is considerably
easier than for the finite line
because we can use cylindrical
symmetry, knowing that all
electric field lines are directed
radially, perpendicular to the line
of charge.
Integrating the 1/r electric field over
rb
rb
 rb 
2k
r , we get ln(r) dependence. 
Va  Vb  Er dr 
dr  2k ln  
If we try setting V=0 at infinity, we
get nonsense since the charge
itself extends to infinity. 
But we can still use the first result to
calculate voltage differences, which
is all we will need. 


ra
ra
 ra 
r

Va  0  2k ln    
 ra 
 rb
Va  Vb  2k ln 
 ra



Showing that electric field lines are
perpendicular to equipotentials
E
E perpendicular
Equipotentials
V constant
V2
E parallel
V1
If there were a component of E parallel to the equipotential, it would
cause a force F =qE in that direction on any charge q. So it could do
work along the equipotential. But no work is done on particles moving
along an equipotential, so E must be perpendicular to the equipotential.
Q.E.D.
Recall 
Conductors in electrostatic equilibrium:
electric field properties from self-consistency
Starting point: In conductors, charges are free to move, both
inside and on the surface. When they have stopped moving,
the excess charges are in “electrostatic equilibrium”.
I.
In electrostatic equilibrium, there is no field inside a conductor.
Otherwise, the charges inside would continue to move! (F = qE)
II. In electrostatic equilibrium, all excess charges are on the surface
of a conductor. Otherwise, there would be electric fields inside!
III. In electrostatic equilibrium, the electric field outside the
conductor, and near the surface, is perpendicular to the surface.
Otherwise, excess charges would continue to move along the surface!
So
Additional properties of conductors
Combining the information on the two previous pages
IV. In electrostatic equilibrium, the surfaces of conductors are
equipotentials. Because, at any point where the electric field
contacts the surface it must be perpendicular to the conductor and to
the local equipotential. The two must coincide.
V. In electrostatic equilibrium, the interior of a conductor is an
equipotential volume at the same potential as its surface. This
argument goes back to the property that there are no electric fields
inside conductors. So there are no forces in the interior to do work on
charges there. And since the interior is continuous with the surface, its
potential matches that of the surface.
These properties greatly simplify the sketching of electric fields
and equipotentials in the presence of conductors.
Electric field and potential of a spherical shell of uniform 
1. Assume this is a
conductor and discuss
E and V in the interior.
2. What would we see if
this is an insulator?
3. Estimate the charge
on the dome of our
Van de Graff machine.
Equipotentials of charged sphere near an infinite plane
1. Do these look like insulators, conductors, or a mix?
2. Discuss point charge near a grounded conducting plane…
 Method of images.
Finding the electric field from the electric potential
So far, we have been using this equation to find the
electric potential when the electric field is known.
 
V    E  ds
But what if we were given the electric potential, and wished to find the
electric field? (The inverse operation.) Let’s look at this in 1D first:
Equation
above in 1D
V    Edx
So for any problem
in 1D we can use:

Ex  
V
x
or

dV d

  E x dx   E x
dx dx
Differentiate both
sides w.r.t. x
Ey  
V
y
or E z  
V
z
Then, the 2D or 3D equation can be found by “reassembling” the vector E:
  V   V   V 

ˆ
ˆ
ˆ
  k  
E  iˆ 
E  i Ex  jE y  kEz
  ˆj 

 x   y 
 z 


ˆ  ˆ  ˆ  
E   i
 j  k V  V
x
x 
 x


E  V
“E = - (the gradient of V)”
Examples: electric field from potential
1. For any example where we have found the potential along some axis
(ring of charge, disk of charge, line of charge, sphere of charge, …) we
can use the following to find (or cross-check) the electric field along that
same axis:
Ex  
V
x
or E y  
V
y
V
or E z  
z
2. For any problem where we are given the potential as a function of x, y,
and z, we can take (-) the gradient of that function in 1D, 2D, or 3D to find


the the vector E as a function of x, y, and z.
E  V
Eg:
V  3x 3  4 xy 2  2 z  6 x 2 z 2  13
Particles in collision. And bound systems such as atoms.
Other potentially interesting examples
Geiger counter