* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download L04_Electric_Potential
Time in physics wikipedia , lookup
Work (physics) wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Maxwell's equations wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Electromagnetism wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Field (physics) wikipedia , lookup
Lorentz force wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Potential energy wikipedia , lookup
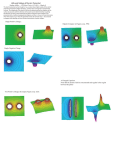
eNERGETICS So far we have been studying electric forces and fields acting on charges. This is the dynamics of electricity. But now we will turn to the energetics of electricity, gaining new insights and new methods for analyzing problems—just as we did in classical mechanics in the first semester. Electric Potential This chapter is about “Electric Potential”. We will approach this topic as follows: From classical mechanics, a quick review: 1. Kinetic energy, work, and potential energy. 2. Mass-spring system, and conservation of total energy. 3. Gravitational potential energy, UG , near Earth (1D). Then, on to electricity: 1. Electric potential energy, UE , in uniform E (1D). 2. Introduce electric potential, VE . 3. Find UE and UG in 3D. 4. Solve problems using electric potential. Kinetic energy, work, and potential energy Kinetic energy, the energy of motion: K = ½ mv2, for any given mass. Work, the transfer of energy: force acting through distance: W Fd or W F d Fd cos( ) or W F ds F cos( ) ds F d Potential energy, U. Energy of position: stored in a system as a result of work. Also known as “pre-integrated work”. Defined only for conservative systems (those without dissipative forces such as friction). Calculating potential energy The “work-energy theorem” states that work done by a system as it moves an object from a to b changes its potential energy: Wab U a U b U Example, spring obeying Hooke’s Law: F = -kx Wab U a U b (U b U a ) U x2 x2 1 1 W Fdx kxdx kx22 kx12 U 2 U1 2 2 x1 x1 U 1 2 kx 2 Energy conservation: Etotal = K + U = ½ mv2 + ½ kx2 = const Gravitational potential energy near Earth’s surface The gravitational force field is nearly uniform and pointed downward, with a constant force: F = -mg yf yf yi yi Work-energy theorem W Fdy mgdy mgy f mgyi U f U i U = mgy Since U depends only on y, any given height is a plane of constant potential energy: an “equipotential”. Energy conservation: Etotal = K + U = = ½ mv2 + mgy = const Examples: Inclined planes, pendulums, roller coasters, Mt. Lemmon, etc. Grand Canyon Topo Map Brown contours are lines of constant altitude: “gravitational equipotentials”. Numbers are feet above sea level. Where lines are closely packed together, the slope is steep: the “gradient” is large. Gravitational equipotentials at Earth’s surface. Discuss slopes (gradients), forces, work, and path independence. ? B Find Do A Saddle points: their contours, and their peculiar equilibrium points Electric potential energy in a uniform electric field The electric force field is uniform (and pointed downward in this example) with a constant force: F = -qE Work-energy theorem yf yf yi yi W Fdy qEdy qEy f qEyi U f U i U = qEy Since U depends only on y, any given height is a plane of constant potential energy: an “equipotential”. Energy conservation: Etotal = K + U = = ½ mv2 + qEy = const Examples: electron microscope beams, linear accelerators, … The electric force is conservative As in the case of gravity, the work done is path independent. What, precisely, is “electric potential”??? Electric potential is the electric potential energy per unit charge: J Units : V (volts) C UE VE V q0 So a particle or object with charge q at a location where the electric potential is V will have a potential energy U = qV. Charged plates again, with given voltages: V U qEy Ed q q E U qV. 600 V V V d m = .2 m from which we can find the electric field, E = (600V – 100V)/(.2 m) = 2500 V/m 100 V Alessandro Giuseppe Antonio Anastasio Volta Invented electrophorus (charging device), the battery (silver, zinc, and brine), discovered methane, ignited gases with electric sparks, … Volt / meter = Newton/Coulomb Volta demonstrating his battery to Napoleone in 1801, by Giuseppe Bertini 1745-1827 V is easily created with batteries or power supplies A charged capacitor We can analyze problems with dynamics or energetics Example: An accelerator/decelerator. (Discuss.) Dynamics: F = ma F = qE = ma a = qE/m Then, we would do kinematic analysis. Conservation of total energy: K + U 1 2 1 2 mvi qVi mv f qV f 2 2 This method can be applied to any system for which we know V ! Two ways to calculate V for new systems 1. As we’ve been doing, start from the work-energy theorem: W U F ds U F ds U V q0 2. Or, notice that if we divide both sides of the middle equation above by the test charge, we can find V directly from the electric field: U F ds q0 q0 V E ds In most cases, we’ll find the second approach more convenient for finding the electric potential. Electric potential of a point charge This result will be the “building block” used to calculate V systems of point charges or continuous charge distributions: r r kq kq kq dr 0 Vr V 2 r r r V Edr r We have chosen the potential to be zero at infinity, giving us this very simple result to carry forward: the electric potential of a point charge. kq V r No vector quantities to complicate things! But we also must be aware of the charge sign, and its effect on V Path independence again Since the electric force is conservative, and the field is central (along the line of centers between charges), the work done on a charge moving between any two points is independent of the path taken. This allows for the definition and calculation of an electric potential, V. The many representations of V for a positive charge kq V r Electric potential obeys the superposition principle For any system of point charges kqi V Vi ri i i For this system of 3 charges: kq1 kq2 kq3 V r1 r2 r3 No vector algebra to fuss with! But, in general we may need to calculate the distances using: ri x xi 2 y yi 2 z zi 2 Where position a is (x,y,z), and the ith charge is at (xi,yi,zi). Equipotentials of familiar charge distributions Equipotentials of a dipole – two representations Do Some potentially interesting examples Electric potential for continuous charge distributions We can find V for continuous charge distributions starting from the equation for a point charge. The method is similar to that used to find F or E, but without the need for vector quantities in the integrand. point charge differential form integrate to find V kq V r kdq dV r dq V k r pick dq based on the given charge distribution 3 dq ds or dq dA or dq dr Turn the crank and the answer will appear… Electric potential of a uniform ring of charge We can avoid doing an integration here! How? Write down the answer “immediately”. Electric potential of a disk of uniform charge Apply the same tactic we used for the electric field of a disk: divide the disk into infinitesimal rings of potential dV, and integrate from 0 to R. Comparing potentials of point charge and disk charge Sketch Electric potential of a finite line of charge Set up Electric potential of an infinite line or cylinder of charge This calculation is considerably easier than for the finite line because we can use cylindrical symmetry, knowing that all electric field lines are directed radially, perpendicular to the line of charge. Integrating the 1/r electric field over rb rb rb 2k r , we get ln(r) dependence. Va Vb Er dr dr 2k ln If we try setting V=0 at infinity, we get nonsense since the charge itself extends to infinity. But we can still use the first result to calculate voltage differences, which is all we will need. ra ra ra r Va 0 2k ln ra rb Va Vb 2k ln ra Showing that electric field lines are perpendicular to equipotentials E E perpendicular Equipotentials V constant V2 E parallel V1 If there were a component of E parallel to the equipotential, it would cause a force F =qE in that direction on any charge q. So it could do work along the equipotential. But no work is done on particles moving along an equipotential, so E must be perpendicular to the equipotential. Q.E.D. Recall Conductors in electrostatic equilibrium: electric field properties from self-consistency Starting point: In conductors, charges are free to move, both inside and on the surface. When they have stopped moving, the excess charges are in “electrostatic equilibrium”. I. In electrostatic equilibrium, there is no field inside a conductor. Otherwise, the charges inside would continue to move! (F = qE) II. In electrostatic equilibrium, all excess charges are on the surface of a conductor. Otherwise, there would be electric fields inside! III. In electrostatic equilibrium, the electric field outside the conductor, and near the surface, is perpendicular to the surface. Otherwise, excess charges would continue to move along the surface! So Additional properties of conductors Combining the information on the two previous pages IV. In electrostatic equilibrium, the surfaces of conductors are equipotentials. Because, at any point where the electric field contacts the surface it must be perpendicular to the conductor and to the local equipotential. The two must coincide. V. In electrostatic equilibrium, the interior of a conductor is an equipotential volume at the same potential as its surface. This argument goes back to the property that there are no electric fields inside conductors. So there are no forces in the interior to do work on charges there. And since the interior is continuous with the surface, its potential matches that of the surface. These properties greatly simplify the sketching of electric fields and equipotentials in the presence of conductors. Electric field and potential of a spherical shell of uniform 1. Assume this is a conductor and discuss E and V in the interior. 2. What would we see if this is an insulator? 3. Estimate the charge on the dome of our Van de Graff machine. Equipotentials of charged sphere near an infinite plane 1. Do these look like insulators, conductors, or a mix? 2. Discuss point charge near a grounded conducting plane… Method of images. Finding the electric field from the electric potential So far, we have been using this equation to find the electric potential when the electric field is known. V E ds But what if we were given the electric potential, and wished to find the electric field? (The inverse operation.) Let’s look at this in 1D first: Equation above in 1D V Edx So for any problem in 1D we can use: Ex V x or dV d E x dx E x dx dx Differentiate both sides w.r.t. x Ey V y or E z V z Then, the 2D or 3D equation can be found by “reassembling” the vector E: V V V ˆ ˆ ˆ k E iˆ E i Ex jE y kEz ˆj x y z ˆ ˆ ˆ E i j k V V x x x E V “E = - (the gradient of V)” Examples: electric field from potential 1. For any example where we have found the potential along some axis (ring of charge, disk of charge, line of charge, sphere of charge, …) we can use the following to find (or cross-check) the electric field along that same axis: Ex V x or E y V y V or E z z 2. For any problem where we are given the potential as a function of x, y, and z, we can take (-) the gradient of that function in 1D, 2D, or 3D to find the the vector E as a function of x, y, and z. E V Eg: V 3x 3 4 xy 2 2 z 6 x 2 z 2 13 Particles in collision. And bound systems such as atoms. Other potentially interesting examples Geiger counter