* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Filtering Actions of Few Probabilistic Effects
Path integral formulation wikipedia , lookup
Renormalization group wikipedia , lookup
Algorithm characterizations wikipedia , lookup
Monte Carlo method wikipedia , lookup
Dijkstra's algorithm wikipedia , lookup
Smith–Waterman algorithm wikipedia , lookup
Pattern recognition wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Drift plus penalty wikipedia , lookup
Reinforcement learning wikipedia , lookup
Simulated annealing wikipedia , lookup
Logical Particle Filtering and
Text Understanding
Hannaneh Hajishirzi
Eyal Amir
University of Illinois at Urbana-Champaign
Erik T. Mueller
IBM TJ Watson Research
Stochastic Filtering
• Tracking the state of a system
Estimate: probability of states at time t
Given: transition model and observations
• Application: partially observable
domains
Robotics, natural language processing
Hidden-Markov models and their applications
Probabilistic planning, POMDPs
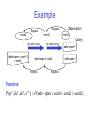
Example of Stochastic Filtering
Initial
states
Query: current position of the robot
Control a dynamic system:
Estimate the final state given past actions and observations
Uncertain initial state
Uncertain effects for actions
Current Models
• Dynamic Bayesian Networks, HMMs
Exact inference (variable elimination)
x1(0)
x1(1)
x1(2)
x1(3)
X2(0)
X2(1)
X2(2)
X2(3)
X3(0)
X3(1)
X3(2)
X3(3)
X4(0)
X4(1)
X4(2)
X4(3)
Approximate inference
……
No conditional
independence
after few steps
Our work improves this
Variational methods
Sequential Monte Carlo sampling
Our Representation
• Fact:
Change in the world occurs by executing actions
Use probabilistic actions instead of conditional
independence
• Transition = Stochastic Choice of Deterministic
Execution
da21
o0
o1
a1
da23
da22
o2
a2
o3
a3
Our Representation: Probabilistic
Relational Action Model
• Language
predicates: At(B,?l2)
constants: Room
variables:?l2
probabilistic actions: Move(?l1,?l2)
deterministic actions: MoveSucc(?l1,?l2)
• Deterministic action axioms
Represent precondition and effects of actions
• Probabilistic action axioms
• Prior distribution
Any framework for representing probabilistic logic
Deterministic Action Axioms
• Represented by preconditions and effects
MvWithObj(B,?l1,?l2):
Precondition: At(B,?l1) and ~At(B,?l2)
Effect:
~At(B,?l1) and At(B,?l2) and
(forall ?o: In(?o) At(?o,?l2))
Probabilistic Action Axioms
Transition: stochastic choice of deterministic execution
partitions
PA(da | a TakeOut(? o), s)
1 In(? o)
PA1 (TakeOutSucc(? o)) 0.8
PA1 (TakeOutFail (? o)) 0.1
PA1 ( Nothing ) 0.1
2 In(? o)
PA2 ( Nothing) 1
Filtering Algorithm (Exact)
da21
o0
da23
da22
o1
a1
o2
a2
o3
a3
P( T | a1:T , o0:T )
T
0:T
1:T
0:T 1
P
(
|
DA
,
o
)
P
(
DA
|
a
,
o
)
DA
T
query (propositional formula over variables at time T)
t
P( t ) sum of probabilities of states that satisfy
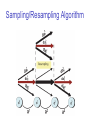
Sampling/Resampling Algorithm
Filtering Algorithm (Approximate)
• First step:
1. Sample deterministic action sequences (FO particles)
2. Update current state formula with that sequence
• Second step:
For each (FO particle, current state)
Compute P(query|FO particle, Current state)
Combine results
Monte Carlo Integration
Pr(query)= 1/N
Σ P(query|FO particle, current state)
FO particle
Update Current State
• First order logical filtering:
FO particle: sequence of deterministic actions
Progressing a formula with deterministic
actions and represent it with another logical
formula
MvWithObj(L1,L2) At(B,L2),In(O),At(O,L2),
In(O)
forall ?o in B: At(?o,L2)
Second Step:
P(Query|FO particle, current state)
Regress query to time 0
Regress current state to time 0
Compute probability of query at time 0 given
the current state at time 0 given the prior
distribution
P( | DA, curF ) P ( | curF )
t
t
0
0
o
Example
Example
Example
Example
Sampling/Resampling Actions
• Sample deterministic actions iteratively
P( DA | a1:T , o0:T 1 )
P(da1 | a1 , o 0 ) P(da t | a1 , da1:t 1 , o 0:t 1 )
t
• Importance function: approximation by ignoring observations
• Weights: dividing approximation over exact distribution
• Resample the current deterministic action when the weights have high
variance
~ T 1:T 0:T
• Finally: PN ( | a , o )
wi P( T | DAi , o0:T )
i
• Drawback: resamples the latest deterministic action
Sampling Actions
• Sample deterministic actions iteratively
P( DA | a1:T , o0:T 1 )
P(da1 | a1 , o 0 ) P(da t | a1 , da1:t 1 , o 0:t 1 )
t
• Sample directly from P(da t | a1 , da1:t 1 , o 0:t 1 )
• Discussions:
Possible because we update the current state at each time
Like rejection sampling
Empirical Results
• Logarithmic scale
• Achieves better accuracy than propositional sampling (SCAI) and
particle filtering (SMC)
• S-Actions better accuracy than S/R-Actions
Experiments:
Different Domain Sizes
0.02
SCAI (vars
SMC (vars
SCAI (vars
SMC (vars
SCAI (vars
SMC (vars
Expected KL-distance
0.016
0.012
8)
8)
9)
9)
10)
10)
0.008
0.004
0
25
50
75
100
500
No. of Samples
Converges faster to the exact value with more samples
Our algorithm (SCAI) is more accurate than sequential Monte Carlo
Experiments:
Different Time-Series Lengths
Expected KL-distance
0.024
SCAI (seq 10)
SMC (seq 10)
SCAI (seq 25)
SMC (seq 25)
SCAI (seq 50)
SMC (seq 50)
0.02
0.016
0.012
0.008
0.004
0
25
50
75
100
500
No. of Samples
Converges to the exact value with more samples
Our algorithm (SCAI) is more accurate with the
same sample size
Summary
• We presented a sampling algorithm for
computing the probability of a posterior given
past actions and observations
Much faster than an exact algorithm
More accurate than particle filtering
FO filtering needs less samples than propositional
sampling
Sampling/Resampling algorithms
• Regression subroutine for stochastic filtering
Sampling deterministic action sequences
Efficient regression with deterministic actions
Application:
Text Understanding
• Understanding a text and answering
questions
• A fundamental problem in Natural Language
Processing and Linguistics
• Very hard to solve (specifically by machines)
Imagine if computers
could understand text
Problem + Use cases
Approaches
Our Approach: Representation, Inference
Future work
Question Answering Systems
Question: Where was President Bush two
years ago?
Ask.com
President Bush said, "Two hundred
thirty-one years ago, …..
Problem + Use cases
Approaches
Our Approach: Representation, Inference
Future work
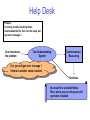
Help Desk
Problem:
I’m having trouble installing Notes.
I downloaded the file, then ran the setup, but
I got error message 1.
User text about
the problem
Text Understanding
System
Commonsense
Reasoning
Yes, you will get error message 1
if there is another notes installed.
Solutions
You must first uninstall Notes.
Then, when you run setup you will
get notes installed
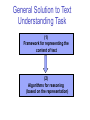
General Solution to Text
Understanding Task
(1)
Framework for representing the
content of text
(2)
Algorithms for reasoning
(based on the representation)
Our Approach
• Represent sentences using event calculus
(a logical framework) + probabilities
Each sentence states properties or actions:
Property: a statement about the world
Action: a change in the world
Probabilities: uncertainty and ambiguity
• Algorithms for stochastic inference
Representation
….John woke up. He flipped the light switch.
He had his breakfast. He went to work….
Text Level
Translation to actions
WakeUp(John, Bed). SwitchLight(John).
Eat(John, Food). Move(John, Work)
Problem + Use cases
Approaches
Our Approach: Representation, Inference
Action Level
Future work
Elements in our Representation
WakeUp(John, Bed). Switch(John,Light). Eat(John, Food). Move(John, Work)
Variables
object
agent: object
physobj: object
location
…
Constants
John: agent
Bedroom: room
HotelRoom: room
Work: location
….
fluents
At(agent, location)
Hungry(agent)
Awake(agent)
LightOn(room)
…
Grounding:
Assignment from variables to constants
At(John, Bedroom)
World state:
Full assignment of {True, False, Unknown} to all the groundings of fluents.
Example:
At(John, Work), ¬ LyingOn(John,Bed), Hungry(John), ¬ OnLight(HotelRoom).
Problem + Use cases
Approaches
Our Approach: Representation, Inference
Future work
Action Declarations
• Recall: Actions change the state of the world
Preconditions
Effects
WakeUp(John, Bed)
Pre: ¬Awake(John), LyingOn(John, Bed)
Eff: Awake(John), ¬LyingOn(John, Bed)
Move (John, Location1, Location2) (simplified)
1. Walk(John, Location1, Location2)
2. Drive(John, Location1, Location2)
Problem + Use cases
Approaches
Our Approach: Representation, Inference
Future work
Transitions
• Stochastic choice of deterministic execution
• Determining each transition using Wordnet:
go, move
drive
fly
run
walk
test drive
soar
hover
skitter
rush
march
step
billow
countermarch
• Finding transition probabilities using:
Context of the sentence + Prior knowledge
Disambiguation techniques:
Go(John, Work)
Walk(John, Work)
Drive(John, Work)
Prior Knowledge
• Knowledge base for state constraints:
At(agent, location1), location1 != location2 ¬At(agent, location2)
AtHand(agent, physobj) ¬OnFloor(physobj)
• Bayes net to represent dependencies:
P(Hungry(agent)|Eat(agent, food))=.8
P(Drive(agent,loc1,loc2)|distance(loc1,loc2)>1m)=.7
• Probabilistic Open Mind (Singh et al., 2002):
Open Mind: You can often find “Object” in “Location”
“You can often find a bed in a bedroom”
“You can often find a bed in a hotel room”
Acquisition of Object Location
Probabilities
• Open Mind: You often find “Object” in “Location”
• Goal: P(object in location)
P(bed in bedroom) > P(bed in hotelroom) > P(bed in hospital)
• Method:
Extract objects list (1600 objects) and locations list (2675 locations)
Use a corpus of American literature stories (downloaded from
Project Gutenberg)
Compute correlations between objects and locations:
Mutual information, KL-distance, Correlation
Probability: P(Near(object, location)|object) We used this
Cross-reference probabilities with Open Mind and normalize
• (Some) Results:
P(bed in bedroom) = 0.5
P(bed in hotelroom) = 0.33
P(bed in hospital) = 0.17
• Add missing assertions to Open Mind
suggested by corpus
Exact Algorithm
• Goal: Answer a question related to text
Question Format: P(Query true) ?
logical formula
• Algorithm:
Consider all possible paths
from root to leaves.
da21
P(Query ) P(Path i ) P(Query | Path i )
i
For each path:
1. Compute P(Query | Path i )
2. Compute P(Path i )
da22
da23
Conclusions and Future Work
• Done: Framework for representing a text and
answering queries
• Evaluate the approximate algorithm (sampling):
Sample most probable paths
• Fill in missing actions:
John woke up. John took shower.
John went to Bathroom.
Solution: If statet-1 conflicts with statet:
FindPath(statet-1,statet)
A Probabilistic planning algorithm
• More powerful prior knowledge
• Learning the preconditions and effects of actions
Thank You
• Elements of our representation:
State variables, world states
Prior graphical model (e.g., Bayes Net)
Transition function for deterministic actions
Probability distribution for probabilistic actions
Represents distribution over deterministic outcomes of
probabilistic actions given current state
Other Domains
Expected KL-distance
Task Details: Filtering
• Input:
Executed action sequence a1:t, with transition
P(s’|s,a)
Received observations (partial) o1:t
• Goal:
Compute belief state P(X(t) | a1:t, o1:t) (time t)
Answer queries over this belief state
• Difficulty: large state spaces
Hard to represent belief state
Conditional independence does not help
Example: Open a Safe
Trying to open a safe with one of the combinations com1, com2, com3
Action: (try-com1)
Com2
Com1
Com3
SafeOpen
P0: Prior distribution
• (try-com1-succ): 0.8
Pre: safe-open ν com1
Eff: safe-open
• (try-com1-fail): 0.2
Pre: safe-open v com1
Eff : ~safe-open
Transition distribution &
Transition function
Sub-Routine:
P(Formula | logical particle, observations)
Algorithm to compute
P( t | DA, o0:t )
t
= Regress ( , DA)
0
Logical particle
1.
2. Ob0 = Regress(o0:t, DA)
(Regression methods [Reiter’01,ShahafAmir07])
Then,
P( t | DA, o0:t ) P 0 ( 0 | Ob o )
Compute probability of the regressed formula given the
regressed observations at time 0 using the graphical-model
prior
Filtering Algorithm (Approximate)
• First step: Sample deterministic action sequences
(samples called logical particles)
da21
da22
da23
Logical
Particle
• Second step: Compute P(query) for each logical
particle
Combine results
Monte Carlo Integration
Pr(query)= 1/N Σ P(query|logical particle,observations)
logical particle
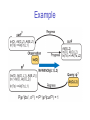
Example
Regress
Regress
~com2
~com2
Observation
~com2
Query
try-com1-succ
(safe-open ν com1)
v com2
try-com2-succ
safe-open ν com2
Regress
safe-open?
safe-open
Regress
Therefore,
P( 2 | da1 , da 2 , o0:2 ) P(safe - open com1 com2 | com2 )
First Step:
Sampling Logical Particles
• Sample from the following distribution:
P( DA | a1:T , o0:T 1 )
P(da1 | a1 , o 0 ) P(da t | a t , da1:t 1 , o 0:t 1 )
t
Sample each deterministic action
Notice:
We sample action sequence with no condition on a state at time 0
Correctness and Analysis
• Convergence to exact value with large
number of samples
• More accurate than particle filtering with the
same number of samples
(smaller expected KL-distance)
• Complexity:
O( Num Samples * T * [T(regression) + T(PFormula)])
Our algorithm is exact for deterministic actions and
provably efficient for many of them.