Download FA15 Lec22 Diffusion

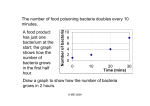
Today:
Diffusion
Why x2 = #Dt (from Equipartition Function)
When directed motion (v ≈ constant, x = vt)
is better/worse than diffusion (v not constant)
depends on how far you have to move.
short distances,
diffusion of small molecules very good.
Biological examples
Bacterial vs. Eukaryotic Cells
Oxygen transport: how close cells need to be to
Oxygen in blood in Lungs
Stopping time of Bacteria.
Diffusion
Move with small kinetic energy
because have Edeg. freedom= ½ kBT.
http://en.wikipedia.org/wiki/Diffusio
n#mediaviewer/File:Blausen_0315
_Diffusion.png
http://commons.wikim
edia.org/wiki/File:Che
mical_surface_diffusio
n_slow.gif#mediaview
er/File:Chemical_surfa
ce_diffusion_slow.gif
Edeg. freedom= ½ kBT = ½ kx2 = ½H Omv2
H2O
m
2
Diffusion
For “small” things, diffusion is a great way to get around.
For somewhat larger things, need directed motors.
Inertia does not matter for bacteria or
anything that is small / microscopic levels.
What is velocity of water molecule at room temperature?
tcollision = ??
Diffusion: x2 = # Dt
Diffusion as a Random Walk
1-D case (first)
Particle at x = 0 at t = 0
1.Assume equally likely to step to right
as step to left.
2. Takes steps of length L every t seconds
i.e. moving with velocity between collisions ±v
(L = ±vt)
R steps/sec; total of N steps
[For now take v, t as constants : they actually depend on
size of particle, nature of fluid, temp…]
Where <x2> is the average
distance squared moved,
D: Diffusion constant
(measured in length2/ time)
L: size of step in time
In reality, there is a distribution of step sizes,
but this model works amazingly well.
In m-dimensions: <DrN2> = 2mDt
(H.W.)
If in 1 sec, it has gone q distance, then in 2 sec it’s gone?
As a function of time, width increases as the √t
What values for D?
Diffusion Coefficient & Brownian Noise
Einstein–one of three 1905 papers, each which
should have received a Nobel Prize
Stokes-Einstein Equation
D = kbT/6phr = kbT/f
h = viscosity (1 centipoise for water)
r = radius of bead
f = frictional coefficient
True where “Reynolds number” is low;
Flow is sufficiently slow that don’t have eddies,
vortexes…is characterized by smooth, constant fluid
motion…flow is laminar, where viscous forces are
dominant.
The Reynolds number is defined as the ratio of inertial
forces to viscous forces and consequently quantifies the
relative importance of these two types of forces for given
flow conditions.
In contrast turbulent flow occurs at high Reynolds
numbers; Where flow is dominated by inertial forces,
which tend to produce chaotic eddies, vortices and other
flow instabilities
D = 250 um2/sec for small molecule in water
Life at low Reynold’s Number
(Where Einstein’s Equation for D holds)
Caramel: no turbulence
(High) Reynold’s number
Neurons: Signals transmitted via
synapses.
Your brain:
100 billion neurons,
100 trillion
synapses
Information
flow
Pre-synaptic
Bouton
Axon
Synapse
(30-100 nm)
Post-synaptic
Spine
Axon
Valtschanoff &
Weinberg, 2003
Dendrite
How long to cross a synapse?
D = 250 mm2/sec
Nerve synapse: 0.1 mm
<x2> = 2Dt
0.01 mm2 = (2)(250 mm2/sec)t
t = 20 msec (fast!)
Diffusion is fast enough
to go across narrow synapse
D: diffusion constant, <x2> = 6 Dt
If molecule gets bigger, x and D
 or

D small molecule , e.g. O2 = 1000 um2/sec: (D=1/f)
Dsucrose = 300 um2/sec (D=1/f)
How long does it take for O2 to go from the edge of
a cell to the middle?
How big cell? 20 um
<x2> = 6Dt
t = <x2>/6D = 16 msec
Ultimately limits the maximum metabolic rate.
Bacterial cell ~ 1-3um in size, eukaryotic 10-50 um
Metabolism of bacteria much higher than eukaryotes.
Size of eukaryotes limited by
size (diffusion time of O2). As
size gets bigger, everything
happens more slowly.
Large cell: frog oocytes–
basically everything happens
slowly.
Every cell needs to be within
50-100 mm of blood supply!
Oocyte:1-2 mm!
If capillary is small enough (and lining relatively free to
move O2 and CO2) diffusion works well.
How Bacteria move
Inertia doesn’t matter for microscopic world
Life at low Reynold’s number
Why study?
1.Simple Example of F= ma
2.Doesn’t need much biology
3.Results are broadly applicable to microscopic level.
Go ~ 25 um/sec: # body lengths/sec?
10 body length/sec
Compared to you walking?
4 miles/hr = 6ft/sec = 1bl/sec
Compared to you swimming?
50 m/s ~ min ~ m/min ~ ½ bl/s
Bacteria are good swimmers!
If turn off “propeller,” how far Bacteria coast?
F = ma
What forces are left on bacteria?
ma = mdv/dt – Ffriction (drag) = -gv
g = drag coefficient
v  linear in v (low Reynold’s #)
What is drag coefficient? What does it depend on?
a) Goopiness of fluid – h = viscosity
b) Dimension of object – bigger object, harder to move
Fdrag = chrv = 6phrv : g = 6phr
r = radius, v = velocity
c= constant
Remember Stokes-Einstein Equation
D = kbT/6phr = kbT/f
h = viscosity (1 centipoise for water)
r = radius of bead
f = frictional coefficient
Fdrag = fv
Solve eq’n of motion:
m dv/dt = -gv
Units of g? (m/v) (v/t) = m/t
(good)
What is mass of bacteria (can you estimate?)
4/3 pr3r = 4 x 10-15kg
What units of g = 6phr
R= 10-6 meters; h = 0.001
g = 20x10-9 N-s/m = 20 nN-s/m
Plugging in the #’s
m = 4 x 10-15kg
g = 20 nN-s/m
t = m/g = 0.2 msec
So bacteria stops in 200 nsec—very fast!
Once forces are turned off, bacteria
forgets about history very quickly!
History doesn’t matter to bacteria.
Inertia is completely irrelevant for bacteria
How far does bacteria coast in 0.2 usec?
Inertia is irrelevant to bacteria.
Once force is over, no forward motion!
Scaling up: What about a person swimming?
A good swimmer coasts about 1 body length
Inertia is much more important
for bigger organism
Size of drag force on bacteria?
(compared to it’s weight?
Bacteria swim as if dragging 10x their own weight!
Class evaluation
1. What was the most interesting thing you
learned in class today?
2. What are you confused about?
3. Related to today’s subject, what would you like
to know more about?
4. Any helpful comments.
Answer, and turn in at the end of class.