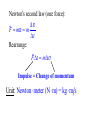Download Chapter 6 Class Notes

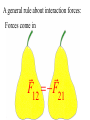
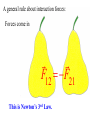
Momentum – Key Ideas
Review – If a force Fx is applied to a
body over a displacement Dx, the
product Fx Dx = (Fcosq)Dx = Work
Review – If a force Fx is applied to a
body over a displacement Dx, the
product Fx Dx = (Fcosq)Dx = Work
If the friction force is less than Fx, the work
increases the object’s Kinetic Energy
1
1
2
Wnet  DKE  m  mo2
2
2
NOW ask: What is the effect of applying
a force over a time interval?
Vocabulary: events in which objects apply forces
to each other are called
INTERACTIONS
NOW ask: What is the effect of applying
a force over a time interval?
Vocabulary: events in which objects apply forces
to each other are called
INTERACTIONS
You predicted the outcomes of some
interactions..
How did you do?
You predicted the outcomes of some
interactions..
How did you do?
A general rule about interaction forces:
A general rule about interaction forces:
Forces come in
F12   F21
A general rule about interaction forces:
Forces come in
F12   F21
This is Newton’s 3rd Law.
The product of mass and velocity
(a vector quantity) is called
momentum (symbol: p)
Definition: p  m
Newton's second law (one force):
D
F  ma  m
Dt
Rearrange:
F Dt  mD
Impulse = Change of momentum
Newton's second law (one force):
D
F  ma  m
Dt
Rearrange:
F Dt  mD
Impulse = Change of momentum
Unit: Newton  meter (N  m) = kg  m s
The impulse is the area under the force vs. time
curve. The average force gives the same impulse
to the object in the time interval Δt as the real
time-varying force.
Conservation of Momentum
The principle of conservation of momentum
states when no external forces act on a system
consisting of two objects that collide with
each other, the total momentum of the system
remains constant in time.
Specifically, the total momentum
before the collision will equal the
total momentum after the collision.
Conservation of Momentum
Mathematically: m1  m22  m1 f  m22 f
Momentum is conserved for the system of
objects.
The system includes all the objects interacting
with each other.
Assumes only internal forces are acting during
the collision.
Can be generalized to any number of objects.
Force as a function of
time for the two colliding
particles.
In all collisions,
total momentum is conserved.
We consider two types of collisions in one
dimension:
1. Totally elastic
2. Totally inelastic
Perfectly Inelastic Collisions
When two objects stick
together after the
collision, they have
undergone a perfectly
inelastic collision.
m1  m22  m1 f  m22 f
1
1
1
1
m1  m22  m1f  m22 f
2
2
2
2
Final velocities:
 f 
m1  m2
2m2
 
2i
m1  m2
m1  m2
 f 
2m1
m  m1
  2
2i
m1  m2
m1  m2
Conservation of
momentum becomes
m1i  m2i2   m1  m2  f
Elastic Collisions
Both momentum and kinetic energy are
conserved.
m1  m22  m1 f  m22 f
1
1
1
1



m1  m22  m1 f  m22 f
2
2
2
2
Final velocities:
m1  m2
2m2
 f 
 
2i
m1  m2
m1  m2
2m1
m2  m1
 f 
 
2i
m1  m2
m1  m2