Download 8/2 Erwin Sitompul University Physics: Wave and Electricity

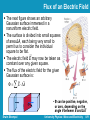
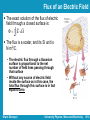
Lecture 8
Ch23. Finding the Electric Field – II
University Physics: Waves and Electricity
Dr.-Ing. Erwin Sitompul
http://zitompul.wordpress.com
Homework 6: Three Particles
Three particles are fixed in place and have charges q1 = q2 =
+p and q3 = +2p. Distance a = 6 μm.
What are the magnitude and direction of the net electric field
at point P due to the particles?
p  1.602  1019 C
e  1.602  1019 C
Erwin Sitompul
University Physics: Wave and Electricity
8/2
Solution of Homework 6: Three Particles
EP ,net  E1  E2  E3
E2

E3
E1
E1  E2  0
 EP ,net  E3  k
EP ,net
r3 P  12 aˆi  12 aˆj
r3P  12 2a
r
rˆ3 P  3 P  12 2iˆ  12 2jˆ
r3 P
 cos  ˆi  sin  ˆj
   45
Erwin Sitompul
• Both fields cancel
one another
q3
r3 P
r̂
2 3P
(2 1.602 1019 )
 8.99 10 1
( 2 2(6 106 ))2
9
 160 N C • Magnitude
EP ,net    45
• Direction
University Physics: Wave and Electricity
8/3
The Electric Field
→
 The calculation of the electric field E can be simplified by
using→symmetry to discard the perpendicular components of
the dE vectors.
 For certain charge distributions involving symmetry, we can
simplify even more by using a law called Gauss’ law,
developed by German mathematician and physicist Carl
Friedrich Gauss (1777–1855).
→
 Instead of considering dE in a given charge distribution,
Gauss’ law considers a hypothetical (imaginary) closed
surface enclosing the charge distribution.
 Gauss’ law relates the electric fields at points on a closed
Gaussian surface to the net charge enclosed by that
surface.
Erwin Sitompul
University Physics: Wave and Electricity
8/4
Flux
→
 Suppose that a wide airstream flows with uniform velocity v
flows through a small square loop of area A.
 Let Φ represent the volume flow rate (volume per unit time) at
which air flows through the loop.
→
 Φ depends on the angle θ between v and the plane of the
loop.
A  A rˆN
Erwin Sitompul
• Unit vector pointing to the normal
direction of the plane
University Physics: Wave and Electricity
8/5
Flux
→
 If v is perpendicular to the plane (or parallel to the plane’s
direction), the rate Φ is equal to vA.
→
 If v is parallel to the plane (or perpendicular to the plane’s
direction), no air moves through the loop, so Φ is zero.
 For an intermediate angle θ, the rate of volume flow through
the loop is:
  (v cos  ) A  v  A
 This rate of flow through an area
is an example of a flux.
 The flux can be interpreted as
the flow of the velocity field
through the loop.
Erwin Sitompul
University Physics: Wave and Electricity
8/6
Flashback: Multiplying Vectors
The Scalar Product
→
→
→→
 The scalar product of the vector a and b is written as a·b
and defined to be:
a  b  ab cos 
→→
 Because of the notation, a·b is also known as the dot
product and is spoken as “a dot b.”
→
→
 If a is perpendicular to b, means Φ = 90°, then the
dot product is equal to zero.
→
→
 If a is parallel to b, means Φ = 0, then the dot product
is equal to ab.
Erwin Sitompul
University Physics: Wave and Electricity
8/7
Flashback: Multiplying Vectors
 The dot product can be regarded as the product of the
magnitude of the first vector and the projection magnitude
of the second vector on the first vector
a  b  ab cos 
 (a cos  )(b)
 (a)(b cos  )
Erwin Sitompul
University Physics: Wave and Electricity
8/8
Flashback: Multiplying Vectors
 When two vectors are in unit vector notation, their dot
product can be written as
ˆ  (b ˆi  b ˆj  b k)
ˆ
a  b  (ax ˆi  a y ˆj  az k)
x
y
z
 axbx  a y by  az bz
 ˆi ˆj kˆ
î 1 0 0
ĵ 0 1 0
k̂ 0 0 1
Erwin Sitompul
University Physics: Wave and Electricity
8/9
Flashback: Multiplying Vectors
→
^
→
^
^
^
What is the angle Φ between a = 3i – 4j and b = –2i + 3k ?
z
Solution:
a  b  ab cos 
3
a  3  (4)  5
2
2

–4
b
–2
y
a
b  (2) 2  32  3.606
3
ˆ
a  b  (3iˆ  4ˆj)  (2iˆ  3k)
ˆ 2i)
ˆ
 (3i)(
 6
x
 ˆi ˆj kˆ
î 1 0 0
ĵ 0 1 0
k̂ 0 0 1
6  (5)(3.606) cos 
6
1
  cos
 109.438
(5)(3.606)
Erwin Sitompul
University Physics: Wave and Electricity
8/10
Flux of an Electric Field
 The next figure shows an arbitrary
Gaussian surface immersed in a
nonuniform electric field.
 The surface is divided into small squares
of area ΔA, each being very small to
permit us to consider the individual
square to be flat.
→
 The electric field E may now be taken as
constant over any given square.
 The flux of the electric field for the given
Gaussian surface is:
   E  A
• Φ can be positive, negative,
or zero, depending
→ on the
→
angle θ between E and ΔA
Erwin Sitompul
University Physics: Wave and Electricity
8/11
Flux of an Electric Field
 The exact solution of the flux of electric
field through a closed surface is:

 E  dA
 The flux is a scalar, and its Si unit is
Nm2/C.
• The electric flux through a Gaussian
surface is proportional to the net
number of field lines passing through
that surface
• Without any source of electric field
inside the surface as in this case, the
total flux through this surface is in fact
equal to zero
Erwin Sitompul
University Physics: Wave and Electricity
8/12
Checkpoint
The figure below shows a Gaussian cube of face area A
immersed in a uniform electric field E that has the positive
direction of the z axis.
In terms of E and A, determine the flux flowing through:
(a) the front face (xy plane) Φ = +EA
Φ = –EA
(b) the rear face
(c) the top face
Φ=0
(d) the whole cube
Φ=0
Erwin Sitompul
University Physics: Wave and Electricity
8/13
Example: Flux of an Electric Field
In a three-dimensional space, a homogenous electric field of
10 N/C is directed down to the negative z direction.
Calculate the flux flowing through:
(a) the square ABCD (xy plane)
z
E
(b) the rectangular AEFG (xz plane)
3
(a)
E  10kˆ V m
AABCD  4kˆ m2
ABCD  E  AABCD
ˆ  (4k)
ˆ
 (10k)
 40 N  m2 C
2
1
F
A
2
(b) AAEFG  6jˆ m
AEFG  E  AAEFG
ˆ  (6ˆj)
 (10k)
0
Erwin Sitompul
G
1
0
B
1
2
3
y
2
3
D
C
x E
University Physics: Wave and Electricity
8/14
Homework 7
(a) The rectangle ABCD is defined by its corner points of
A(2,0,0), B(0,3,0), C(0,3,2.5), and D(2,0,2.5). Draw a sketch
of the rectangular.
→
^
^
(b) Given an electric field of E = –2i + 6j N/C, draw the electric
field on the sketch from part (a).
(c) Determine the number of flux crossing the area of the
rectangular ABCD.
Erwin Sitompul
University Physics: Wave and Electricity
8/15
Homework 7
New
(a) The triangle FGH is defined by its corner points of F(2,0,0),
G(0,3,0), and H(0,0,4). Draw
a sketch of the triangle.
→
^
^
(b) Given an electric field of E = –2i + 6j N/C, draw the electric
field on the sketch from part (a).
(c) Determine the number of flux crossing the area of the
triangle FGH.
Erwin Sitompul
University Physics: Wave and Electricity
8/16