Download Chapter TM28

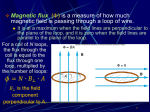
General electric flux definition
• The field is not
uniform
• The surface is not
perpendicular to the
field
E
E

n̂
A
 
 E  E nˆ A  E A cos 
A
N


 E   E i nˆ i A i
i 1
If the surface is made up of a
mosaic of N little surfaces
ˆ
 E   E ndA
  E dA
Magnetic Flux
ˆ
 B   B ndA
  B dA
Whenever possible:
B  B A
Units: [Weber] = [Wb]=[T-m2]
Gauss’s Law
Gauss asserts that the calculation for the flux through a
closed surface from a point charge is true for any
charge distribution!!!
E 
 E dA  4kq
enclosed
q enclosed

o
This is true so long as Q is the charge
enclosed by the surface of integration.
Gauss’s Law for magnetism
B 
 B dA  0
This is true because we cannot isolate a magnetic pole and
because magnetic field lines are continuous. The net number
of field lines passing through any surface is always zero!
Faraday’s Law
When the magnet moves, a
current is induced as if there
was a source of emf (like a
battery) in the circuit!
Active Figure 31.1
(SLIDESHOW MODE ONLY)
Faraday’s Law
Active Figure 31.2
(SLIDESHOW MODE ONLY)
Faraday’s Law of Induction
• An induced emf is produced by a changing
magnetic field.
• Lenz’s Law – An induced emf is always in a
direction that opposes the original change in
the flux that caused the emf.
d B
emf    
dt
Units: [Volts]
How can we change the flux?
d B
emf    
dt
• Change flux by:
– Change area
– Change angle
– Change field
ˆ
 B   B ndA
  B dA
30.
In Figure P31.30, the bar magnet is moved toward
the loop. Is Va – Vb positive, negative, or zero? Explain.
Figure P31.30
Faraday’s Law – continued
• Remember B is the magnetic flux through
the circuit and is found by
 B   B  dA
• If the circuit consists of N loops, all of the
same area, and if B is the flux through one
loop, an emf is induced in every loop and
Faraday’s law becomes
dB
ε  N
dt
Decaying uniform magnetic field
P31.4
Assume we can change field:
B
A
B  Boe t / 
R
 B  Bo Ae t / 
• Change flux by:
– Change field
– Change area
– Change angle
d B
emf    

dt
Bo A  t / 

e

d  Bo Ae t /  
dt
 Bo A  t / 
I 
e
R
R
Applications of Faraday’s Law –
Pickup Coil
• The pickup coil of an electric guitar
uses Faraday’s law
• The coil is placed near the
vibrating string and causes a
portion of the string to become
magnetized
• When the string vibrates at the
same frequency, the magnetized
segment produces a changing flux
through the coil
• The induced emf is fed to an
amplifier
1.
A 50-turn rectangular coil of dimensions 5.00 cm × 10.0
cm is allowed to fall from a position where B = 0 to a new
position where B = 0.500 T and is the magnetic field directed
perpendicular to the plane of the coil. Calculate the magnitude of
the average emf that is induced in the coil if the displacement
occurs in 0.250 s.
3.
A 25-turn circular coil of wire has diameter 1.00 m. It is
placed with its axis along the direction of the Earth’s magnetic
field of 50.0 μT, and then in 0.200 s it is flipped 180°. An average
emf of what magnitude is generated in the coil?
6.
A magnetic field of 0.200 T exists within a solenoid of
500 turns and a diameter of 10.0 cm. How rapidly (that is,
within what period of time) must the field be reduced to zero, if
the average induced emf within the coil during this time interval
is to be 10.0 kV?
Linear Generator
Charges stop moving when:
FE  FB
qE  qvB
V
 vB
V  vB
Linear Generator with Faraday’s Law
Area  
 x 
 B   B dA  B A  B x

d B
d


B x
dt
dt
dx
 B
 B v
dt
By Lenz’s Law, what is the direction of current?
I
B v
R

Active Figure 31.10
(SLIDESHOW MODE ONLY)
Power moving the bar
PF v
 B v
 B
Fbar  I  B  
 R 


 B v
B2 2 v 2
 Bv
P
 R 
R


2 2 2
2 2 2


B
v
B
v
2
PI R 
R 
2
R
 R 
Same result!
Breaking effect if power not added
B2 2 v
dv
Fbar  I  B  
m
R
dt
dv B2 2

v0
dt mR
v  vo e
B2 2

t
mR
12.
A 30-turn circular coil of radius 4.00 cm and resistance 1.00 Ω is
placed in a magnetic field directed perpendicular to the plane of the coil. The
magnitude of the magnetic field varies in time according to the expression B
= 0.010 0t + 0.040 0t2, where t is in seconds and B is in tesla. Calculate the
induced emf in the coil at t = 5.00 s.
19.
An automobile has a vertical radio antenna 1.20 m long. The
automobile travels at 65.0 km/h on a horizontal road where the Earth’s
magnetic field is 50.0 μT directed toward the north and downward at an
angle of 65.0° below the horizontal. (a) Specify the direction that the
automobile should move in order to generate the maximum motional emf in
the antenna, with the top of the antenna positive relative to the bottom. (b)
Calculate the magnitude of this induced emf.
22.
A conducting rod of length ℓ moves on two
horizontal, frictionless rails, as shown in Figure
P31.20. If a constant force of 1.00 N moves the bar
at 2.00 m/s through a magnetic field B that is
directed into the page, (a) what is the current through
the 8.00-Ω resistor R? (b) What is the rate at which
energy is delivered to the resistor? (c) What is the
mechanical power delivered by the force Fapp?
Rotating Generators and
Faraday’s Law
 B   B dA  B A  B A cos 

 B  B A cos t
d B
d

  B A cos t
dt
dt
 B
0
  o  t
A  sin t
   N B
A  sin t

For N loops of wire
Induced emf in a Rotating Loop
• The induced emf in
the loop is
dB
ε  N
dt
 NABω sin ωt
• This is sinusoidal,
with max = NAB
Active Figure 31.21
(SLIDESHOW MODE ONLY)
Rotating Generators
DC Generators
• The DC (direct
current) generator has
essentially the same
components as the AC
generator
• The main difference is
that the contacts to the
rotating loop are made
using a split ring
called a commutator
Active Figure 31.23
(SLIDESHOW MODE ONLY)
32.
For the situation shown in Figure P31.32, the
magnetic field changes with time according to the
expression B = (2.00t3 – 4.00t2 + 0.800)T, and r2 = 2R =
5.00 cm. (a) Calculate the magnitude and direction of the
force exerted on an electron located at point P2 when t =
2.00 s. (b) At what time is this force equal to zero?
45.
A proton moves through a uniform electric field E = 50.0 j V/m and a
uniform magnetic field B = (0.200i + 0.300j + 0.400k)T. Determine the
acceleration of the proton when it has a velocity v = 200 i m/s.
59.
A circular loop of wire of radius r is in a
uniform magnetic field, with the plane of the loop
perpendicular to the direction of the field (Fig. P31.59).
The magnetic field varies with time according to B(t) = a
+ bt, where a and b are constants. (a) Calculate the
magnetic flux through the loop at t = 0. (b) Calculate the
emf induced in the loop. (c) If the resistance of the loop is
R, what is the induced current? (d) At what rate is energy
being delivered to the resistance of the loop?
Eddy Currents
Self-Inductance
• When the switch is
closed, the current
does not immediately
reach its maximum
value
• Faraday’s law can be
used to describe the
effect
Self-induced emf
• A current in the coil produces a magnetic field directed
toward the left (a)
• If the current increases, the increasing flux creates an
induced emf of the polarity shown (b)
• The polarity of the induced emf reverses if the current
decreases (c)
Self Inductance
B  o nI
d  o nIA 
d B
dI
NBA dI
  N
 N
  No nA  
dt
dt
dt
I dt
N B dI
dI

 L
I dt
dt
Define: Self Inductance
N B
L
I
Inductance of a Solenoid
• The magnetic flux through each turn is
 N 
 B  BA   μo I  A


• Therefore, the inductance is
N B μo N 2 A
L

I
• This shows that L depends on the geometry
of the object
Inductance Units
dI
  L
dt
N B
L
I
 V 
L
    s    Henry    H 

A /s
3.
A 2.00-H inductor carries a steady current of 0.500 A.
When the switch in the circuit is opened, the current is
effectively zero after 10.0 ms. What is the average induced emf
in the inductor during this time?
5.
A 10.0-mH inductor carries a current I = Imax sin ωt,
with Imax = 5.00 A and ω/2π = 60.0 Hz. What is the back emf
as a function of time?
7.
An inductor in the form of a solenoid contains 420
turns, is 16.0 cm in length, and has a cross-sectional area of
3.00 cm2. What uniform rate of decrease of current through the
inductor induces an emf of 175 μV?
LR Circuits
Charging
Kirchhoff Loop Equation:
dI
Vo  RI  L  0
dt
Solution:
I
Vo
1  e t /  

R
L

R
LR Circuits
Discharging
Kirchhoff Loop Equation:
dI
RI  L  0
dt
Solution:
I  Io e t / 
L

R
Active Figure 32.3
(SLIDESHOW MODE ONLY)
14.
Calculate the resistance in an RL circuit in which L =
2.50 H and the current increases to 90.0% of its final value in
3.00 s.
20.
A 12.0-V battery is connected in series with a resistor
and an inductor. The circuit has a time constant of 500 μs, and
the maximum current is 200 mA. What is the value of the
inductance?
24.
A series RL circuit with L = 3.00 H and a series RC
circuit with C = 3.00 μF have equal time constants. If the
two circuits contain the same resistance R, (a) what is the
value of R and (b) what is the time constant?
Energy in a coil
 dI 
P  VI   L  I
 dt 
PE in an Inductor
1 2
U  LI
2
PE in an Capacitor
1
U  CV 2
2
Energy Density in a coil
1 2
U  LI
2
PE in an Inductor
N B NBA N  o NI /
L


I
I
I
A
B
I
o N
1  N   o N  A  B 
1 2
U 
B A

 
2
2 o
  o N 
2
1 2
u
B
2 o

1
u  o E 2
2
31.
An air-core solenoid with 68 turns is 8.00 cm long and
has a diameter of 1.20 cm. How much energy is stored in its
magnetic field when it carries a current of 0.770 A?
33.
On a clear day at a certain location, a 100-V/m vertical
electric field exists near the Earth’s surface. At the same place,
the Earth’s magnetic field has a magnitude of 0.500 × 10–4 T.
Compute the energy densities of the two fields.
36.
A 10.0-V battery, a 5.00-Ω resistor, and a 10.0-H
inductor are connected in series. After the current in the circuit
has reached its maximum value, calculate (a) the power being
supplied by the battery, (b) the power being delivered to the
resistor, (c) the power being delivered to the inductor, and (d)
the energy stored in the magnetic field of the inductor.
Example 32-5: The Coaxial Cable
• Calculate L for the cable
• The total flux is
 B   B dA  
b
a
μo I
μo I
b
dr 
ln  
2πr
2π
a
• Therefore, L is
 B μo
b
L

ln  
I
2π  a 
• The total energy is
1 2 μo I 2  b 
U  LI 
ln  
2
4π
a
Mutual Inductance
N212  I1
N 212  M12 I1
 M12 I1 
d

N
d12
dI1

2 
2   N2
  N2
 M12
dt
dt
dt
dI 2
1   M 21
dt
Mutual Inductance example
B1   0
N1
12  B1A   0
I1
N1
 N1

d  0
I1A 
d 21
   N1 N 2 A dI
2   N2
  N2 
0
dt
dt
dt
M12  0
N1 N 2
AM
I1A
Induced emf and Electric Fields
• An electric field is created in the conductor as
a result of the changing magnetic flux
• Even in the absence of a conducting loop, a
changing magnetic field will generate an
electric field in empty space
• This induced electric field is nonconservative
– Unlike the electric field produced by stationary charges
• The emf for any closed path can be expressed as
the line integral of E.ds over the path
General form of Faraday’s Law
Ub  Ua
Vba  Vb  Va 
   E ds
q
a
b
So the electromotive force around a closed path is:
 E d
And Faraday’s Law becomes:
d B
 E d 
dt
A changing magnetic flux produces an electric field.
This electric field is necessarily non-conservative.
E produced by changing B
d B
 E d 
dt
E 2r  r
d
B
2
dt
rdB
E 
2 dt
How about outside ro ?
Maxwell’s Equations
q
S E  dA  εo
 B  dA  0
Gauss's law  electric 
Gauss's law in magnetism
S
dB
 E  ds   dt
Faraday's law
dE
 B  ds  μo I  εo μo dt
Ampere-Maxwell law
•The two Gauss’s laws are symmetrical, apart from the absence of the term for
magnetic monopoles in Gauss’s law for magnetism
•Faraday’s law and the Ampere-Maxwell law are symmetrical in that the line
integrals of E and B around a closed path are related to the rate of change of
the respective fluxes
•
•
•
•
•
•
•
•
Gauss’s law (electrical):
The total electric flux through any
closed surface equals the net charge
inside that surface divided by o
This relates an electric field to the
charge distribution that creates it
Gauss’s law (magnetism):
The total magnetic flux through
any closed surface is zero
This says the number of field lines
that enter a closed volume must
equal the number that leave that
volume
This implies the magnetic field
lines cannot begin or end at any
point
Isolated magnetic monopoles have
not been observed in nature
q
S E  dA  εo
 B  dA  0
S
•
•
•
•
Faraday’s law of Induction:
This describes the creation of an electric field by a
changing magnetic flux
The law states that the emf, which is the line
integral of the electric field around any closed
path, equals the rate of change of the magnetic flux
through any surface bounded by that path
One consequence is the current induced in a
conducting loop placed in a time-varying B
•
The Ampere-Maxwell law is a generalization of
Ampere’s law
•
It describes the creation of a magnetic field by an
electric field and electric currents
The line integral of the magnetic field around any
closed path is the given sum
•
dB
 E  ds   dt
dE
 B  ds  μo I  εo μo dt
The Lorentz Force Law
• Once the electric and magnetic fields are known at
some point in space, the force acting on a particle
of charge q can be calculated
• F = qE + qv x B
• This relationship is called the Lorentz force law
• Maxwell’s equations, together with this force law,
completely describe all classical electromagnetic
interactions
Voltage transformers
 solenoid
 NP 
  o
IP  A


d B
Vs  N s
dt
d B
VP  N P
dt
NS  NP  step up transformer
NP  NS  step down transformer
d B VP VS


dt
N P NS
Current transformers
PPr imary  PSecondary
VP IP  VSIS
IP
NS
VS 
VP
NP
IS
NP IP  NSIS
Example: transformers
Vp  110V
IP
N p  916
Ns  100
IS
What is Vs ?