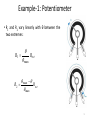* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture-10-11-12: Mathematical Modeling of
Alternating current wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Electrification wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Three-phase electric power wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Voltage optimisation wikipedia , lookup
Commutator (electric) wikipedia , lookup
Electric machine wikipedia , lookup
Opto-isolator wikipedia , lookup
Potentiometer wikipedia , lookup
Brushless DC electric motor wikipedia , lookup
Rectiverter wikipedia , lookup
Dynamometer wikipedia , lookup
Electric motor wikipedia , lookup
Induction motor wikipedia , lookup
Variable-frequency drive wikipedia , lookup
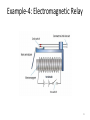
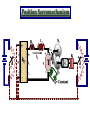
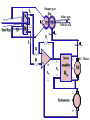
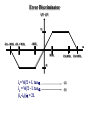
Feedback Control Systems (FCS) Lecture-10-11 Mathematical Modelling of Real World Systems Dr. Imtiaz Hussain email: [email protected] URL :http://imtiazhussainkalwar.weebly.com/ 1 Modelling of Mechanical Systems • Automatic cruise control • A throttle is the mechanism by which the flow a of constant a fluid is vehicle The purpose of the cruise control system is to maintain speed despite external disturbances, such as changes inmanaged wind or road grade. by obstruction. • This is accomplished by measuring the vehicle speed, comparing it to the desired speed, and automatically adjusting the throttle. • The resistive forces, bv, due to rolling resistance and wind drag act in the direction opposite to the vehicle's motion. 2 Modelling of Mechanical Systems u mv bv • The transfer function of the systems would be V (s) 1 U ( s ) ms b 3 Modelling of Mechanical Systems • Consider a simple pendulum shown below. 4 Electromechanical Systems • Electromechanics combines electrical and mechanical processes. • Devices which carry out electrical operations by using moving parts are known as electromechanical. – – – – – Relays Solenoids Electric Motors Electric Generators Switches and e.t.c 5 Introduction • Micro-electromechanical (MEMS) systems is the technology of very small devices. • It merges at the nano-scale into nanoelectromechanical systems(NEMS) and nanotechnology. 6 Example-1: Potentiometer 7 Example-1: Potentiometer • The resistance between the wiper (slider) and "A" is labeled R1, the resistance between the wiper and "B" is labeled R2. • The total resistance between "A" and "B" is constant, R1+R2=Rtot. • If the potentiometer is turned to the extreme counterclockwise position such that the wiper is touching "A" we will call this θ=0; in this position R1=0 and R2=Rtot. • If the wiper is in the extreme clockwise position such that it is touching "B" we will call this θ=θmax; in this position R1=Rtot and R2=0. 8 Example-1: Potentiometer • R1 and R2 vary linearly with θ between the two extremes: R1 max Rtot max R2 Rtot max 9 Example-1: Potentiometer • Potentiometer can be used to sense angular position, consider the circuit below. • Using the voltage divider principle we can write: eout R1 R1 ein ein R1 R2 Rtot eout max ein 10 Example-2: Loud Speaker • A voltage is typically applied across the terminals of the loudspeaker and the "cone" moves in and out causing pressure waves perceived as sound. 11 Example-2: Loud Speaker • The speaker consists of a fixed magnet that produces a uniform magnetic field of strength β. • The speaker has a cone with mass (M), that moves in the x direction. • The cone is modelled with a spring (K) to return it to its equilibrium position, and a friction (B). • Attached to the cone, and within the magnetic field is a coil of wire or radius "a." The coil consists of "n" turns and it moves along with the cone. • The wire has resistance (R) and inductance (L). 12 Example-2: Loud Speaker • Mechanical Free body Diagram f e Mx Bx kx Electrical Schematic di ein iR L em dt 13 Example-2: Loud Speaker f e Mx Bx kx di ein iR L em dt • Force on a current carrying conductor in a magnetic field is given by f e il • Where ℓ is the total length of wire in the field. • It is equal to the circumference of the coil (2·π·a) times the number of turns (n). • That is, ℓ=2·π·a·n). i 2an Mx Bx kx (1) 14 Example-2: Loud Speaker di ein iR L em dt • Back EMF is given by em lx 2anv di 2anx ein iR L dt (2) • To find the transfer function X(S)/Ein(s) we have to eliminate current i. 15 Example-2: Loud Speaker i 2an Mx Bx kx (1) di 2anx ein iR L dt (2) • Taking Laplace transform of equations (1) and (2) considering initial conditions to zero. 2anI( s ) Ms2 X ( s ) BsX ( s ) kX( s ) (3) 2ansX ( s ) Ein ( s ) I ( s )R LsI ( s ) (4) • Re-arranging equation (3) as Ms 2 X ( s ) BsX ( s ) kX ( s ) I (s) 2an 16 Example-2: Loud Speaker • Put I(s) in equation (4) Ms 2 X ( s ) BsX ( s ) kX ( s ) Ms 2 X ( s ) BsX ( s ) kX ( s ) 2ansX ( s ) Ein ( s ) R Ls 2an 2an • After simplification the transfer function is calculated as X (s) 2an 3 Ein ( s ) ( s LM s 2 ( RM LB ) s( RB LK 4 2 a 2 n 2 ) RK ) 17 Example-3: Capacitor Microphone • The system consists of a capacitor realized by two plates, one is fixed and the other is movable but attached to a spring. 18 Example-4: Electromagnetic Relay 19 Example-5: Push Button 20 Example-6: D.C Drives • Speed control can be achieved using DC drives in a number of ways. • Variable Voltage can be applied to the armature terminals of the DC motor . • Another method is to vary the flux per pole of the motor. • The first method involve adjusting the motor’s armature while the latter method involves adjusting the motor field. These methods are referred to as “armature control” and “field control.” 21 Example-6: D.C Drives • Motor Characteristics • For every motor, there is a specific Torque/Speed curve and Power curve. • Torque is inversely proportional to the speed of the output shaft. • Motor characteristics are frequently given as two points on this graph: • The stall torque,, represents the point on the graph at which the torque is maximum, but the shaft is not rotating. • The no load speed is the maximum output speed of the motor. 22 Example-6: D.C Drives • Motor Characteristics • Power is defined as the product of torque and angular velocity. 23 Example-6.1: Armature Controlled D.C Motor Ra Input: voltage u Output: Angular velocity La B u ia eb T J Elecrical Subsystem (loop method): dia u Ra ia La eb , dt Mechanical Subsystem Tmotor Jω Bω where eb back-emf voltage Example-6.1: Armature Controlled D.C Motor Ra La Power Transformation: Torque-Current: Voltage-Speed: B u Tmotor K t ia ia eb T J eb K b ω where Kt: torque constant, Kb: velocity constant For an ideal motor Kt Kb Combing previous equations results in the following mathematical model: dia Ra ia K b ω u La dt Jω B-K t ia 0 Example-6.1: Armature Controlled D.C Motor Taking Laplace transform of the system’s differential equations with zero initial conditions gives: La s Ra I a(s) K b Ω(s) U(s) Js B Ω(s)-K t I a(s) 0 Eliminating Ia yields the input-output transfer function Kt Ω(s) U(s) La Js 2 JRa BLa s BRa K t K b Example-6.1: Armature Controlled D.C Motor Reduced Order Model Assuming small inductance, La 0 K t Ra Ω(s) U(s) Js B K t K b Ra which is equivalent to K t K b Ra B K t u Ra • The D.C. motor provides an input torque and an additional damping effect known as back-emf damping Example-6.1: Armature Controlled D.C Motor If output of the D.C motor is angular position θ then we know Ra d dt or La B ( s ) s ( s ) ia u eb J T θ Which yields following transfer function K t Ra U(s) sJs B K t K b (s) Ra Example-6.2: Field Controlled D.C Motor Ra Rf if ef Lf Tm J B ω Applying KVL at field circuit ef if Rf Lf Mechanical Subsystem Tm Jω Bω di f dt La ea Example-6.2: Field Controlled D.C Motor Power Transformation: Torque-Current: Tm K f i f where Kf: torque constant Combing previous equations and taking Laplace transform (considering initial conditions to zero) results in the following mathematical model: E f ( s ) R f I f ( s ) sL f I f ( s ) Js( s ) B( s ) K f I f ( s ) Example-6.2: Field Controlled D.C Motor Eliminating If(S) yields Kf Ω(s) E f (s) Js B ( L f s R f ) If angular position θ is output of the motor Ra Rf if ef Lf Tm La J B θ (s) E f (s) Kf sJs B ( L f s R f ) ea Example-6.3 An armature controlled D.C motor runs at 5000 rpm when 15v applied at the armature circuit. Armature resistance of the motor is 0.2 Ω, armature inductance is negligible, back emf constant is 5.5x10-2 v sec/rad, motor torque constant is 6x10-5, moment of inertia of motor 10-5, viscous friction coeffcient is negligible, moment of inertia of load is 4.4x10-3, viscous friction coeffcient of load is 4x10-2. La Ra ea 15 v ia N1 Bm eb T Jm BL JL N2 L 1. Drive the overall transfer function of the system i.e. ΩL(s)/ Ea(s) 2. Determine the gear ratio such that the rotational speed of the load is reduced to half and torque is doubled. System constants ea = armature voltage eb = back emf Ra = armature winding resistance = 0.2 Ω La = armature winding inductance = negligible ia = armature winding current Kb = back emf constant = 5.5x10-2 volt-sec/rad Kt = motor torque constant = 6x10-5 N-m/ampere Jm = moment of inertia of the motor = 1x10-5 kg-m2 Bm=viscous-friction coefficients of the motor = negligible JL = moment of inertia of the load = 4.4x10-3 kgm2 BL = viscous friction coefficient of the load = 4x10-2 N-m/rad/sec gear ratio = N1/N2 Example-6.3 Since armature inductance is negligible therefore reduced order transfer function of the motor is used. Kt ΩL(s) U(s) J eq Ra Beq La s Beq Ra K t K b La Ra ea 15 v ia N1 Bm eb T Jm BL JL N2 2 N J eq J m 1 J L N2 L 2 N Beq Bm 1 BL N2 Example-6.4 A field controlled D.C motor runs at 10000 rpm when 15v applied at the field circuit. Filed resistance of the motor is 0.25 Ω, Filed inductance is 0.1 H, motor torque constant is 1x10-4, moment of inertia of motor 10-5, viscous friction coefficient is 0.003, moment of inertia of load is 4.4x10-3, viscous friction coefficient of load is 4x10-2. Ra Rf ef if Lf La ea Tm Bm ωm N1 Jm BL JL N2 L 1. Drive the overall transfer function of the system i.e. ΩL(s)/ Ef(s) 2. Determine the gear ratio such that the rotational speed of the load is reduced to 500 rpm. Position Servomechanism + + e kp r _ La Ra + ea _ N1 + ia JM BM T eb _ BL θ JL N2 - if = Constant c Numerical Values for System constants r = angular displacement of the reference input shaft c = angular displacement of the output shaft θ = angular displacement of the motor shaft K1 = gain of the potentiometer shaft = 24/π Kp = amplifier gain = 10 ea = armature voltage eb = back emf Ra = armature winding resistance = 0.2 Ω La = armature winding inductance = negligible ia = armature winding current Kb = back emf constant = 5.5x10-2 volt-sec/rad K = motor torque constant = 6x10-5 N-m/ampere Jm = moment of inertia of the motor = 1x10-5 kg-m2 Bm=viscous-friction coefficients of the motor = negligible JL = moment of inertia of the load = 4.4x10-3 kgm2 BL = viscous friction coefficient of the load = 4x10-2 N-m/rad/sec n= gear ratio = N1/N2 = 1/10 System Equations e(t)=K1[ r(t) - c(t) ] or E(S)=K1 [ R(S) - C(S) ] (1) Ea(s)=Kp E(S) (2) Transfer function of the armature controlled D.C motor Is given by θ(S) Ea(S) = Km S(TmS+1) System Equations (contd…..) Where K Km = RaBeq+KKb And Tm RaJeq = RaBeq+KKb Also Jeq=Jm+(N1/N2)2JL Beq=Bm+(N1/N2)2BL Output gear ia o b Sun Ray L 1/n A Solar axis o Vehicle axis B m Rf ib R R m _ Servo + + eo _ + es _ Amplifier Ka + D.C Motor ea M _ _ Tachometer et + Input & Output variables Solar axis r o Center of output gear Vehicle axis Error Discriminator ia(t) - ib(t) 2I -C/L – W/2L -C/L + W/2L - W/2L W/2L C/L-W/2L -2I ia= W/2 + L tan ib = W/2 - L tan (ia-ib)/ = 2L (A) (B) C/L+W/2L Operational amplifier & Servo Amplifier The out of op-amp is eo =-RF (ia-ib) Transfer function is given by: eo/(ia-ib)= -RF Similarly output of servo amplifier is es = -K ea Transfer function is given by: es / ea = -K D.C Motor & Output Gear Transfer function of the D.C motor is given by: θm / ea = Ki /(S2 Ra J + S Ra B + Ki Kb) Output Gear θo = 1/n θm θo/θm = 1/n Tachometer et = S kt θm et/θm = S kt To download this lecture visit http://imtiazhussainkalwar.weebly.com/ END OF LECTURES-10 46