* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download (a) n
Copenhagen interpretation wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum group wikipedia , lookup
Quantum teleportation wikipedia , lookup
Ferromagnetism wikipedia , lookup
Quantum key distribution wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Molecular orbital wikipedia , lookup
Particle in a box wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Renormalization wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Canonical quantization wikipedia , lookup
Quantum state wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Double-slit experiment wikipedia , lookup
Tight binding wikipedia , lookup
EPR paradox wikipedia , lookup
History of quantum field theory wikipedia , lookup
Matter wave wikipedia , lookup
Hidden variable theory wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Wave–particle duality wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Atomic theory wikipedia , lookup
Atomic orbital wikipedia , lookup
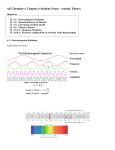
Chemistry Second Edition Julia Burdge Lecture PowerPoints Jason A. Kautz University of Nebraska-Lincoln 6 Quantum Theory and the Electronic Structure of Atoms Copyright (c) The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 1 6 Quantum Theory and the Electronic Structure of Atoms 6.1 The Nature of Light Properties of Waves The Electromagnetic Spectrum The Double-Slit Experiment 6.2 Quantum Theory Quantization of Energy Photons and the Photoelectric Effect 6.3 Bohr’s Theory of the Hydrogen Atom Atomic Line Spectra The Line Spectrum of Hydrogen 6.4 Wave Properties of Matter The de Broglie Hypothesis Diffraction of Electrons 6.5 Quantum Mechanics The Uncertainty Principle The Schrödinger Equation The Quantum Mechanical Description of the Hydrogen Atom 6 Quantum Theory and the Electronic Structure of Atoms 6.6 Quantum Numbers Principal Quantum Number (n) Angular Momentum Quantum Number (l) Magnetic Quantum Number (ml) Electron Spin Quantum Number (ms) 6.7 Atomic Orbitals s Orbitals p Orbitals d Orbitals and other High-Energy Orbitals Energies of Orbitals 6.8 Electron Configuration Energies of Atomic Orbitals in Many-Electron Systems The Pauli Exclusion Principle The Aufbau Principle Hund’s Rule General Rules for Writing Electron Configurations 6.9 Electron Configurations and the Periodic Table 6.1 The Nature of Light Visible light is only a small component of the continuum of radiant energy known as the electromagnetic spectrum. The Nature of Light All forms of electromagnetic radiation travel in waves. Waves are characterized by: Wavelength (λ; lambda) – the distance between identical points on successive waves Frequency (ν; nu) – the number of waves that pass through a particular point in 1 second. Amplitude – the vertical distance from the midline of a wave to the top of the peak or the bottom of the trough. The Nature of Light The speed of light (c) through a vacuum is a constant: c = 3.00 x 108 m/s Speed of light, frequency and wavelength are related: c = λν λ is expressed in meters ν is expressed in reciprocal seconds (s−1) The Nature of Light An electromagnetic wave has both an electric field component and a magnetic component. The electric and magnetic components have the same frequency and wavelength. The Nature of Light When light passes through two closely spaced slits, an interference pattern is produced. Constructive interference is a result of adding waves that are in phase. Destructive interference is a result of adding waves that are out of phase. The Nature of Light What is the wavelength of light (in meters) of an electromagnetic wave whose frequency is 1.61 x 1012 s−1? Solution: Step 1: Rearrange the equation below to calculate wavelength: c = λν 3.00 108 m/s 4 = = = 1.86 10 m 12 1 1.61 10 s c 6.2 Quantum Theory When a solid is heated, it emits electromagnetic radiation, known as blackbody radiation, over a wide range of wavelengths. The amount of energy given off at a certain temperature depends on the wavelength. Classical physics failed to completely explain the phenomenon. Max Planck suggested that radiant energy is only emitted or absorbed in discrete quantities or bundles. A quantum of energy is the smallest quantity of energy that can be emitted (or absorbed). E = hν h is called Planck’s constant: 6.63 x 10−34 J•s Quantum Theory A quantum of energy is the smallest quantity of energy that can be emitted (or absorbed). E = hν E is the energy (in Joules) ν is the frequency h is called Planck’s constant: 6.63 x 10−34 J•s Energy is always emitted in whole-number multiples of hν. Quantum Theory Albert Einstein used Planck’s theory to explain the photoelectric effect. Electrons are ejected from the surface of a metal exposed to light of a certain threshold frequency. The number of electrons ejected is proportional to the intensity. Einstein proposed that the beam of light is really a stream of particles. These particles of light are now called photons. Quantum Theory Each photon (of the incident light) must posses the energy given by the equation: Ephoton = hν where ν is at minimum the threshold frequency. hν = KE + W KE is the kinetic energy of the ejected electron W is the binding energy of the electron Quantum Theory Calculate the wavelength (in nm) of light with an energy of 7.85 x 1019 J per photon. In what region of the electromagnetic radiation does this light fall? Solution: Step 1: Rearrange the equation below to calculate frequency. Ephoton = hν = Ephoton h 7.85 1019 J 15 1 = = 1.184 10 s 6.63 1034 J s Quantum Theory Calculate the wavelength (in nm) of light with an energy of 7.85 x 1019 J per photon. In what region of the electromagnetic radiation does this light fall? Solution: Step 2: Rearrange the equation below to calculate wavelength. c = λν 3.00 108 m/s 7 = = = 2.534 10 m 15 1 1.184 10 s c Quantum Theory Calculate the wavelength (in nm) of light with an energy of 7.85 x 1019 J per photon. In what region of the electromagnetic radiation does this light fall? Solution: Step 3: Convert to nm. 2.534 10 7 1 nm m = 253 nm 9 1 10 m Quantum Theory Solution: Step 4: Correlate the wavelength (or frequency) to the electromagnetic spectrum. 235 nm is in the ultraviolet region of the electromagnetic spectrum 6.3 Bohr’s Theory of the Hydrogen Atom Sunlight is composed of various color components that can be recombined to produce white light. The emission spectrum of a substance can be seen by energizing a sample of material with some form of energy. The “red hot” or “white hot” glow of an iron bar removed from a fire is the visible portion of its emission spectrum. All wavelengths of visible light are present in the emission spectra of sun light and a heated solid. Bohr’s Theory of the Hydrogen Atom Line spectra are the emission of light only at specific wavelengths. Bohr’s Theory of the Hydrogen Atom Every element has its own unique emission spectrum. Bohr’s Theory of the Hydrogen Atom The Rydberg equation can be used to calculate the wavelengths of the four visible lines in the emission spectrum of hydrogen. 1 1 = R 2 2 n1 n2 1 R∞ is the Rydberg constant (1.09737317 x 107 m−1) λ the wavelength of a line in the spectrum n1 and n2 are positive integers where n1 > n2. Bohr’s Theory of the Hydrogen Atom Neils Bohr attributed the emission of radiation by an energized hydrogen atom to the electron dropping from a higher-energy orbit to a lower one. As the electron dropped, it gave up a quantum of energy in the form of light. Bohr showed that the energies of the electron in a hydrogen atom are given by the equation: En = 2.18 10 En is the energy n is a positive integer 18 1 J 2 n Bohr’s Theory of the Hydrogen Atom As an electron gets closer to the nucleus, n decreases. En = 2.18 10 18 1 J 2 n En becomes larger in absolute value (but more negative) as n gets smaller. En is most negative when n = 1 A free electron is considered to be infinitely far from the nucleus. n = ∞ and E∞ = 0 Bohr’s Theory of the Hydrogen Atom For hydrogen, the lowest energy (most stable) state occurs when n = 1 En = 2.18 10 18 1 J 2 n The lowest energy state is called the ground state. The stability of the electron decreases as n increases. Each energy state in which n > 1 is called an excited state. Bohr’s Theory of the Hydrogen Atom During an emission, an electron drops from an excited state to a lower energy state. nf is the final state ni is the initial state E = h = 2.18 10 18 1 1 J 2 2 nf ni Bohr’s Theory of the Hydrogen Atom E = h = 2.18 10 nf is the final state ni is the initial state 18 1 1 J 2 2 nf ni Bohr’s Theory of the Hydrogen Atom To calculate wavelength, substitute c/λ for ν and rearrange: E = h = 2.18 10 18 1 1 J 2 2 nf ni 2.18 1018 J 1 1 = 2 2 hc nf ni 1 Bohr’s Theory of the Hydrogen Atom What is the wavelength (in nm) of a photon emitted during a transition from the n = 3 state to the n = 1 state in the H atom? Solution: Step 1: Use the equation below to solve for λ. 2.18 1018 J 1 1 = 2 2 hc nf ni 1 1 1 2.18 1018 J 1 = = 9742572 m (6.63 1034 J s)(3.00 108 m/s) 12 32 1 λ = (9742572 m−1)−1 = 1.03 x 10−7 m Bohr’s Theory of the Hydrogen Atom What is the wavelength (in nm) of a photon emitted during a transition from the n = 3 state to the n = 1 state in the H atom? Solution: Step 2: Convert to nm. 1.03 10 7 1 nm m = 103 nm 9 1 10 m 6.4 Wave Properties of Matter Louis de Broglie reasoned that if light can behave like a stream of particles (photons), then electrons could exhibit wavelike properties. According to deBroglie, electrons behave like standing waves. Only certain wavelengths are allowed. At a node, the amplitude of the wave is zero. Wave Properties of Matter De Broglie deduced that the particle and wave properties are related by the following expression: = h mu λ is the wavelength associated with the particle m is the mass (in kg) u is the velocity (in m/s) The wavelength calculated from this equation is known as the de Broglie wavelength. Wave Properties of Matter Calculate the de Broglie wavelength (in nm) of a hydrogen atom (m = 1.674 x 10‒27 kg) moving at 15.0 m/s. Solution: Step 1: Use the equation below to calculate wavelength: h = mu 6.63 1034 kg m2 / s 4 = 2.64 10 m 31 (1.674 10 kg)(15.0 m/s) Step 2: Convert m to nm: 2.64 104 m 1 nm 5 = 2.64 10 nm 9 1 10 m Wave Properties of Matter Experiments have shown that electrons do indeed posses wavelike properties: X-ray diffraction pattern of aluminum foil Electron diffraction pattern of aluminum foil. 6.5 Quantum Mechanics The Heisenberg uncertainty principle states that it is impossible to know simultaneously both the momentum and the position of a particle with certainty. x p h 4 Δx is the uncertainty in position in meters Δp is the uncertainty in momentum x mu Δu is the uncertainty in velocity in m/s m is the mass in kg h 4 Quantum Mechanics If an electron in the hydrogen atom has a velocity of 5 x 106 m/s +− 1 percent. What is the uncertainty in position? Solution: Step 1: Calculate Δu: Δu = 0.01 x (5 x 106 m/s) = 5 x 104 m/s Quantum Mechanics If an electron in the hydrogen atom has a velocity of 5 x 106 m/s +‒ 1 percent. What is the uncertainty in position? Solution: Step 2: Rearrange the equation below to solve for Δx: h x mu 4 h x 4 mu The minimum uncertainty in position is 1 x 10‒9 m = 10 Å. This is about 10 times larger than the atom! 6.63 1034 kg m2 /s 9 x 1 10 m 31 4 4 (9.11 10 kg)(5 10 m/s) Quantum Mechanics Erwin Schrödinger derived a complex mathematical formula to incorporate the wave and particle characteristics of electrons. Wave behavior is described with the wave function ψ. The probability of finding an electron in a certain area of space is proportional to ψ2 and is called electron density. Quantum Mechanics The Schrödinger equation specifies possible energy states an electron can occupy in a hydrogen atom. The energy states and wave functions are characterized by a set of quantum numbers. Instead of referring to orbits as in the Bohr model, quantum numbers and wave functions describe atomic orbitals. 6.6 Quantum Numbers Quantum numbers are required to describe the distribution of electron density in an atom. There are three quantum numbers necessary to describe an atomic orbital. The principal quantum number (n) – specifies size The angular moment quantum number (l) – specifies shape The magnetic quantum number (ml) – specifies orientation Quantum Numbers The principal quantum number (n) designates the size of the orbital. Larger values of n correspond to larger orbitals. The allowed values of n are integral numbers: 1, 2, 3 and so forth. The value of n corresponds to the value of n in Bohr’s model of the hydrogen atom. A collection of orbitals with the same value of n is frequently called a shell. Quantum Numbers The angular moment quantum number (l) describes the shape of the orbital. The values of l are integers that depend on the value of the principal quantum number The allowed values of l range from 0 to n – 1. l 0 1 2 3 Orbital designation s p d f A collection of orbitals with the same value of n and l is referred to as a subshell. Quantum Numbers The magnetic quantum number (ml) describes the orientation of the orbital in space. The values of ml are integers that depend on the value of the angular moment quantum number: – l,…0,…+l Quantum Numbers Quantum numbers designate shells, subshells, and orbitals. Quantum Numbers The electron spin quantum number (ms) is used to specify an electron’s spin. There are two possible directions of spin. Allowed values of ms are +½ and −½. Quantum Numbers A beam of atoms is split by a magnetic field. Statistically, half of the electrons spin clockwise, the other half spin counterclockwise. Quantum Numbers To summarize quantum numbers: principal (n) size Required to describe an atomic orbital angular (l) shape magnetic (ml) orientation principal (n = 2) 2px related to the magnetic quantum number (ml ) angular momentum (l = 1) electron spin (ms) direction of spin Required to describe an electron in an atomic orbital Quantum Numbers Which of the following are possible sets of quantum numbers? Quantum number (a) (b) (c) Principal (n) 1 2 3 Angular moment (l) 1 0 2 Magnetic (ml) 0 0 –2 Electron spin (ms) +½ +½ –½ Solution: Step 1: The principle quantum number must be a positive integral number. (a) n = 1 (b) n = 2 (c) n = 3 Quantum Numbers Which of the following are possible sets of quantum numbers? Quantum number (a) (b) (c) Principal (n) 1 2 3 Angular moment (l) 1 0 2 Magnetic (ml) 0 0 –2 Electron spin (ms) +½ +½ –½ Solution: Step 2: The angular momentum quantum number has allowed values of 0 to n–1. (a) n = 1, l = 1 not allowed set (a) is not possible (b) n = 2, l = 0 (c) n = 3, l = 2 Quantum Numbers Which of the following are possible sets of quantum numbers? Quantum number (a) (b) (c) Principal (n) 1 2 3 Angular moment (l) 1 0 2 Magnetic (ml) 0 0 –2 Electron spin (ms) +½ +½ –½ Solution: Step 3: The magnetic quantum number has allowed values of –l,...0,...+l. (b) n = 2, l = 0, ml = 0 (c) n = 3, l = 2, ml = –2 Quantum Numbers Which of the following are possible sets of quantum numbers? Quantum number (a) (b) (c) Principal (n) 1 2 3 Angular moment (l) 1 0 2 Magnetic (ml) 0 0 –2 Electron spin (ms) +½ +½ –½ Solution: Step 4: Electron spin has two allowed values +½ and –½. (b) n = 2, l = 0, ml = 0, ms = +½ (b) is a possible set (c) n = 3, l = 2, ml = –2, ms = –½ (c) is a possible set 6.7 Atomic Orbitals All s orbitals are spherical in shape but differ in size: 1s < 2s < 3s principal quantum number (n = 2) 2s angular momentum quantum number (l = 0) ml = 0; only 1 orientation possible Atomic Orbitals The p orbitals: Three orientations: l = 1 (as required for a p orbital) ml = –1, 0, +1 Atomic Orbitals The d orbitals: Five orientations: l = 2 (as required for a d orbital) ml = –2, –1, 0, +1, +2 Atomic Orbitals The energies of orbitals in the hydrogen atom depend only on the principal quantum number. the 3d subshell (n = 3; l = 2) the n = 2 shell 6.8 Electron Configuration The electron configuration describes how the electrons are distributed in the various atomic orbitals. In a ground state hydrogen atom, the electron is found in the 1s orbital. Ground state electron configuration of hydrogen Energy principal (n = 1) 2s 1s 2p 2p 2p 1 1s number of electrons in the orbital or subshell angular momentum (l = 0) The use of an up arrow indicates and electron with ms = + ½ Electron Configuration If hydrogen’s electron is found in a higher energy orbital, the atom is in an excited state. A possible excited state electron configuration of hydrogen Energy 1 2s 2s 1s 2p 2p 2p Electron Configuration The helium emission spectrum is more complex than the hydrogen spectrum. There are more possible energy transitions in a helium atom. Electron Configuration In a multi-electron atoms, the energies of the atomic orbitals are split. Splitting of energy levels refers to the splitting of a shell into subshells of different energies Electron Configuration According to the Pauli exclusion principle, no two electrons can have the same four quantum numbers. The ground state electron configuration of helium Energy 2p 2p 2p 2 1s 2s Quantum number Principal (n) 1s describe the 1s orbital Angular moment (l) Magnetic (ml) describes the electrons in the 1s orbital Electron spin (ms) 1 0 0 +½ 1 0 0 ‒½ Electron Configuration The Aufbau principle states that electrons are added to the lowest energy orbitals first before moving to higher energy orbitals. The third electron must go in the next available orbital with the lowest possible energy. The ground state electron configuration of Li 2 1 1s 2s Energy 2p 2p 2p Li has a total of 3 electrons 2s 1s The 1s orbital can only accommodate 2 electrons (Pauli exclusion principle) Electron Configuration The Aufbau principle states that electrons are added to the lowest energy orbitals first before moving to higher energy orbitals. The ground state electron configuration of Be 2 2 1s 2s Energy 2p 2s 1s 2p 2p Be has a total of 4 electrons Electron Configuration The Aufbau principle states that electrons are added to the lowest energy orbitals first before moving to higher energy orbitals. The ground state electron configuration of B 2 2 1 1s 2s 2p Energy 2p 2s 1s 2p 2p Electron Configuration According to Hund’s rule, the most stable arrangement of electrons is the one in which the number of electrons with the same spin is maximized. The ground state electron configuration of C 2 2 2 1s 2s 2p Energy 2p 2p 2p 2s The 2p orbitals are degenerate. 1s Put 1 electron in each before pairing (Hund’s rule). Electron Configuration According to Hund’s rule, the most stable arrangement of electrons is the one in which the number of electrons with the same spin is maximized. The ground state electron configuration of N 2 2 3 1s 2s 2p Energy 2p 2s 2p 2p The 2p orbitals are degenerate. Put 1 electron in each before pairing (Hund’s rule). 1s Electron Configuration According to Hund’s rule, the most stable arrangement of electrons is the one in which the number of electrons with the same spin is maximized. The ground state electron configuration of O 2 2 4 1s 2s 2p Energy 2p 2s 1s 2p 2p Once all the 2p orbitals are singly occupied, additional electrons will have to pair with those already in the orbitals. Electron Configuration General rules for writing electron configurations: 1) Electrons will reside in the available orbitals of the lowest possible energy. 2) Each orbital can accommodate a maximum of two electrons. 3) Electrons will not pair in degenerate orbitals if an empty orbital is available. 4) Orbitals will fill in the order indicated in the figure. Electron Configuration Write the electron configuration for a Si atom (Z = 14). Solution: Fill in the energy diagram following the rules for electron configurations. 3p 3p 3p 2p 2p 2p Energy 3s 2s Electron configuration of Si 1s22s22p63s23p2 1s 6.9 Electron Configurations and the Periodic Table The electron configurations of all elements except hydrogen and helium can be represented using a noble gas core. The ground state electron configuration of K: 1s22s22p63s23p64s1 [Ar] 1 [Ar]4s Electron Configurations and the Periodic Table Elements in Group 3B through Group 1B are the transition metals. Electron Configurations and the Periodic Table There are several notable exceptions to the order of electron filling for some of the transition metals. Cr [Ar] 4s 3d 3d 3d 3d 3d Greater stability with half-filled 3d subshell Cu [Ar] 4s 3d 3d 3d 3d 3d Greater stability with filled 3d subshell Electron Configurations and the Periodic Table Write the electron configuration for an iron atom (Z = 26) Solution: Step 1: Locate the noble gas in the period above Fe. This is the noble gas core. Argon core Electron Configurations and the Periodic Table Write the electron configuration for an iron atom (Z = 26) Solution: Step 2: Write the remaining electron configuration [Ar] 4s23d5 Electron Configurations and the Periodic Table Electron Configurations and the Periodic Table 6 Chapter Summary: Key Points The Nature of Light Properties of Waves The Electromagnetic Spectrum The Double-Slit Experiment Quantum Theory Quantization of Energy Photons and the Photoelectric Effect Bohr’s Theory of the Hydrogen Atom Atomic Line Spectra The Line Spectrum of Hydrogen Wave Properties of Matter The de Broglie Hypothesis Diffraction of Electrons Quantum Mechanics The Uncertainty Principle The Schrödinger Equation The Quantum Mechanical Description of the Hydrogen Atom Quantum Numbers (n,l,ml,ms) Atomic Orbitals s orbitals, p orbitals, d orbitals and other High-Energy Orbitals 6 Chapter Summary: Key Points Energies of Orbitals Electron Configuration Energies of Atomic Orbitals in Many-Electron Systems The Pauli Exclusion Principle The Aufbau Principle Hund’s Rule General Rules for Writing Electron Configurations Electron Configurations and the Periodic Table