Download Thursday, August 26

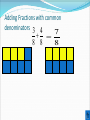
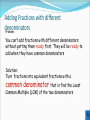
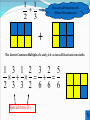
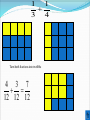
Thursday, August 26
Bell Work
 Fill in planner
 Pr. 1-4/1-5 (EVENS)
 Agenda for Today
 Grade Practice 1-3
 Notes
 Group Work
 Assignment
Bell Work Answers
Sample Map Item
Objective
 SWBAT
 Add and subtract real numbers using models and rules
Real Number Addition Rules
 If the signs are the same, pretend the
signs aren’t there. Add the absolute
values and then put the sign of the
addends in front of your answer.
9 + 3.5 = 12.5
-9 + -3.5 = -12.5
 If the signs are different, subtract the smaller
absolute value from the larger one. Then, put
the sign of the real number with the larger
absolute value in front of your answer.
Larger abs. value
9–2=7
-9 + 2 =
Answer
=-7
Using a Number Line to Add Integers
When the number is positive, count
to the right.
When the number is negative, count
to the left.
-
+
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
3 + -5 =
-2
+
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-
6 + -4 = +2
+
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-
3 + -7 = -4
+
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-
-3 + 7 = +4
-
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
+
Use your number line to solve
-3 + -5 =
-8
3
-4 + 7 =
3 + 4 =
7
-6 + 7 =
1
14
5 + 9 =
-9 + -9 =
-18
Adding Integers Matching
Subtracting a negative number is the
same as adding a positive. Change the
signs and add.
2 – (-7)
is the same as
2 + (+7)
2 + 7 = 9!
-3 - 2
is the same as
-3 + (-2)
-3+(-2)=-5
5-7
is the same as
5 + (-7)
5 + -7 = -2
Try a few…
1. 8 – (-12) = ?
2. 22 – (-30) =?
3. – 17 – (-3) = ?
4. –52 – 5 = ?
Check Your Answers
1. 8 – (-12) = 8 + 12 = 20
2. 22 – (-30) = 22 + 30 = 52
3. – 17 – (-3) = -17 + 3 = -14
4. –52 – 5 = -52 + (-5) = -57
Adding Fractions with common
denominators 3 4
7


8
8 8
Adding Fractions with different
denominators
Problem:
You can’t add fractions with different denominators
without getting them ready first. They will be ready to
add when they have common denominators
Solution:
Turn fractions into equivalent fractions with a
common denominator
that is find the Least
Common Multiple (LCM) of the two denominators
Finding the
Lowest Common Denominator
 The lowest common multiple of two numbers is
the lowest number in BOTH lists of multiples
1 1

2 3
Multiples of 2 are 2, 4, 6, 8, 10……
Multiples of 3 are 3, 6, 9, 12, ………
What is the lowest common
multiple?
Finding the
Lowest Common Denominator
 The lowest common multiple of two numbers is
the lowest number they will BOTH divide into
1 1

2 3
2 divides into 2, 4, 6, 8…..
3 divides into 3, 6, 9….
What is the lowest number 2 and 3
both divide into?
1 1

2 3
You can’t add fractions with
different denominators
+
The Lowest Common Multiple of 2 and 3 is 6 so turn all fractions into sixths
1 3 1 2 3 2 5
     
2 3 3 2 6 6 6
Special form of 1
1
2

2
5
Lowest common denominator is 10 so make all fractions tenths
5 4 9
 
10 10 10
1
1

3
4
Turn both fractions into twelfths
4 3
7
 
12 12 12
?
?
3 3 2 7
2
9 14 23
   




1
3 7 3 7
21 21 21 21 21 21
It is 3/3
It is 7/7
So I multiply
So I multiply
3/7 by 3/3
2/3 by 7/7
Finally the fractions are READY to
add. I just have to add the
numerators
9+14=23
What
is special
the
lowest
What
What
special
form
formnumber
3 and
77divide
ofBOTH
1 of
will1 change
will
change
3 into?
to 21.
to 21.
Hmmmm?
Hmmmm?
It is 21.
So
that is my
Hmmmmm??????
common denominator
Now 3x3=9 and 2x7=14
Now I know the new
numerators
Adding Mixed Numbers
 Separate the fraction and the whole number sections, add
them separately and recombine at the end
22
11
22

 55
11
33



7

5
6
7

5
6

Decimal and Fraction Examples
 2.3  4.5
Think: I have different signs, so I need to
subtract the absolute values.
4.5  2.3  2.2
Think: Which number had the larger
absolute value in my given problem?
2.2
Think: My answer is positive because 4.5
has a larger absolute value than 2.3
Decimal and Fraction Examples
 14.1  (3.2)
Think: I have the same signs, so I will add
the absolute values.
14.1  3.2  17.3
Think: I will keep the sign of the numbers
in the expression
 17.3
Think: My answer is negative because
both numbers in the expression were
negative!
Decimal and Fraction Examples
12.25  (1.4)
Think: I’m going to change this to
addition by adding the opposite of -1.4
12.25  1.4
Think: I better line up my decimal points.
12.25
 1 .4
13.65
Decimal and Fraction Examples
1 2 Think: I need to find a common
denominator before I can add these
 
4 3 fractions.
3 8 Think: Ok, I have different signs, so I need
to subtract the absolute values.
 
12 12
8 3
5
 
12 12 12
Think: I have to take the sign of the
number with the higher absolute value, so
my answer will be positive.
5
12
Decimal and Fraction Examples
1 3 Think: I need to find a common
denominator before I can add these

10 5 fractions.
1 6 Think: I’m going to end up with a negative
result. I’m going to change this problem

10 10 to adding a negative fraction.
Think: My denominator will stay the
1
6
same. 1 + (-6)= -5, so that is my
 (  ) numerator.
10
10
5
1
 
10
2
What is a matrix?
 A rectangular arrangement of rows and numbers.
Sue
Mary
Jane
Week
1
-6
8.6
11
Week
2
2.3
5
-3
Bob
Georg
e
Fred
Week
1
7
-5.4
2
Week
2
11.1
3
-1
Adding Matrices
Who Won?
Sue and
Bob
Mary
and
George
Jane and
Fred
Week 1
1
3.2
13
Week 2
13.4
8
-4
Winner
-2
-11
6
-2
-17.4
-11
5
1
18
4
-4
1.5
-16
-9
-1/8
5/4 -1
Subtraction practice
 (Do these on the back of your
quick check)
 9.9  3.8
4  ( 5)
 9.3  (8.1)
[ ]
3
2
-1
3
-
]
7 12
7 -4
-4 2
]
Objective
 SWBAT
 Add and subtract real numbers using models and rules