Download Picture

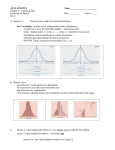
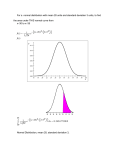
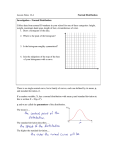
The Practice of Statistics – Chapter 1 Reading
1.1A:
Pages 2 – 6
Statement
T or F
1.
Statistics is the science of data.
T
F
2.
Individuals are the “What” of the data.
T
F
3.
A variable is a characteristic of an individual
T
F
4.
All numbers are classified as quantitative data.
T
F
5.
The type of data determines how to analysis and graph
the information
T
F
6.
A variable generally takes values that vary.
T
F
7.
A distribution is the way something is divided up or
spread out.
T
F
8.
When exploring data, first look at the numeric
summaries (mean, standard deviation, median, etc.)
T
F
9.
Inference is the process of reaching a conclusion for a
population based on the data from a sample.
T
F
1.1B:
If False, make a correct statement
Pages 7 – 11
Statement
T or F
10. The distribution of a categorical variable list the
categories and gives the count of individuals who fall
within each category.
T
F
11. A pie chart or histogram display the distribution of a
categorical variable more vividly.
T
F
12. A pie chart must include all the categories that make
up a whole.
T
F
13. Pie charts are used to emphasize each category’s
relation to the whole.
T
F
14. In a bar graph, the bar heights show the category
counts or percents.
T
F
15. When drawing a bar graph, make the bars equally
wide.
T
F
16. To increase eye appeal on a bar graph, replace bars
with pictures.
T
F
If False, make a correct statement
1.1C:
Pages 11 – 19
Statement
T or F
17. When analyzing a two-way table, begin by looking at
the distribution of each variable separately.
T
F
18. On a two-way table, if the row and column total are
missing, these totals should be calculated first.
T
F
19. The marginal distribution of one of the categorical
variables in a two-way table of counts is the
distribution of values of that variable among all
individual described by the table.
T
F
20. Counts are often more informative than percents.
T
F
21. Marginal distributions tell us about the relationship
between two variables.
T
F
T
F
T
F
T
F
T
F
T
F
22. A conditional distribution of a variable describes the
values of that variable among individuals who have a
specific value of another variable.
23. A segmented bar graph is used to compare the
distribution of a categorical variable in each of several
groups.
24. An association between two variables is when
knowing the value of one variable will not help predict
the value of the second.
25. If there is no association between two variables, then
the segmented bar graph for the two variables would
look the same.
26. If two variables are strongly associated, they may be
influenced by a segmented variable.
1.2A:
If False, make a correct statement
Pages 25 – 33
Statement
T or F
27. One of the simplest graphs to construct is a line graph.
T
F
28. The purpose of making a graph is to help understand
the data,
T
F
29. In any graph, look for the overall pattern and for
striking departures from that pattern.
T
F
30. You can describe the overall pattern of a distribution
by it shape and center.
T
F
31. An outlier is an individual value that falls outside the
overall pattern.
T
F
32. When you describe the shape of the distribution,
concentrate on all the ups and downs.
T
F
33. When you describe the shape of the distribution, look
for clusters of values, obvious gaps, and potential
outliers.
T
F
If False, make a correct statement
34. A skewed distribution is when one side of the graph is
much longer than the other.
T
F
35. The direction of the skewness is the direction of where
most of the data are clustered and not in the direction
of the long tail.
T
F
36. A unimodal distribution have a single clear peak
whereas a bimodal has two clear peaks.
T
F
37. A stemplot gives us a quick picture of the shape of a
distribution while including the actual numerical
values in the graph.
T
F
38. Stem plots work well with large data sets.
T
F
39. When creating a stemplot, it is a good idea to round
numbers so that the final digit after rounding is
suitable as a leaf.
T
F
40. One of the simplest graphs to construct is a line graph.
T
F
41. The purpose of making a graph is to help understand
the data,
T
F
42. In any graph, look for the overall pattern and for
striking departures from that pattern.
T
F
43. You can describe the overall pattern of a distribution
by it shape and center.
T
F
44. An outlier is an individual value that falls outside the
overall pattern.
T
F
45. When you describe the shape of the distribution,
concentrate on all the ups and downs.
T
F
46. When you describe the shape of the distribution, look
for clusters of values, obvious gaps, and potential
outliers.
T
F
47. A skewed distribution is when one side of the graph is
much longer than the other.
T
F
48. The direction of the skewness is the direction of where
most of the data are clustered and not in the direction
of the long tail.
T
F
49. A unimodal distribution have a single clear peak
whereas a bimodal has two clear peaks.
T
F
50. A stemplot gives us a quick picture of the shape of a
distribution while including the actual numerical
values in the graph.
T
F
51. Stem plots work well with large data sets.
T
F
52. When creating a stemplot, it is a good idea to round
numbers so that the final digit after rounding is
suitable as a leaf.
T
F
1.2B:
Pages 33– 40
Statement
T or F
53. In making a histogram, first divide the data into classes
of equal width.
T
F
54. In making a histogram, second find how many of the
individuals belong in each class.
T
F
55. In making a histogram, third label and scale your axes
and draw the histogram.
T
F
56. In a histogram, eight classes is a good minimum.
T
F
57. A histogram is the same thing as a bar graph.
T
F
58. When comparing distributions with different numbers
of observations, it is a good practice to use percents
instead of counts.
T
F
59. When a graph looks nice, the data will have meaning.
T
F
1.3A:
If False, make a correct statement
Pages 48 – 59
Statement
T or F
60. The most common measure of center is the mean.
T
F
61. When symbol, 𝑥̅ , is the symbol used for the mean of a
population.
T
F
62. The mean is sensitive to the influence of extreme
observations.
T
F
63. The median is the balancing point of the distribution.
T
F
64. In a symmetrical distribution the mean and median
are close to equal.
T
F
65. When a distribution is skewed, use the mean to
describe the center.
T
F
66. A useful numerical description require3s both a
measure of center and a measure of spread.
T
F
67. The range of a distribution is the largest value minus
the smallest value.
T
F
68. IQR = Q1 – Q3
T
F
69. The quartiles and interquartile range is resistant
because they are not affected by a few extreme
values.
T
F
70. An outlier is any value that falls more than 1.5 x IQR
above the third quartile or below the first quartile.
T
F
If False, make a correct statement
71. The five-number summary consists of Min, Q1, Mean,
Q3, and Max.
T
F
72. Use the five-number summary to construct a box plot.
T
F
73. Boxplots are best used to show side-by-side
comparison of more than one distribution.
T
F
1.3B:
Pages 60 – 67
Statement
T or F
74. The standard deviation and variance measure spread
by looking at how far the observations are from their
mean.
T
F
75. 𝑠𝑥 is the symbol used for the standard deviation of a
sample.
T
F
76. The standard deviation is 0 when all values in a data
set are equal.
T
F
77. The standard deviation is measured in the same units
as the original observation.
T
F
78. If a distribution is symmetrical, use the mean for the
center and the IQR for the spread.
T
F
79. All summaries should include a plot of the data.
T
F
If False, make a correct statement
The Practice of Statistics – Chapter 2 Reading
2.1A:
Pages 85 – 91
Statement
T or F
1.
The 70th percentile of a distribution is the value with
70% of the observation less than it.
T
F
2.
To make a cumulative relative frequency graph, we
plot a point corresponding to the cumulative relative
frequency in each class at the smallest value of the
next class.
T
F
3.
The first quartile is equal to the 25th percentile.
T
F
4.
We describe the location of a value in a distribution by
how many standard deviation it is away from the
median.
To standardize a value, subtract the mean of the
distribution and then divide the difference by the
standard deviation.
T
F
T
F
5.
6.
A z-score tells us how many standard deviation from
the mean an observation falls and in what direction.
T
F
7.
We often standardize observations only if they are on
the same scale.
T
F
2.1B:
If False, make a correct statement
Pages 92 – 97
Statement
T or F
8.
Transforming data converts the observation form the
original units of measurement to a standardized scale.
T
F
9.
Adding a number to each value in a distribution will
not change the mean.
T
F
10. Adding a number to each value in a distribution will
not change the standard deviation.
T
F
11. Adding a number to each value in a distribution will
not change the shape.
T
F
12. Multiplying a number to each value in a distribution
will not change the mean.
T
F
13. Multiplying a number to each value in a distribution
will not change the standard deviation.
T
F
14. Multiplying a number to each value in a distribution
will not change the shape.
T
F
If False, make a correct statement
2.2A:
Pages 104 – 117
Statement
T or F
15. A density curve is a curve has an area of exactly 1
underneath it.
T
F
16. A density curve can describe exactly the real data.
T
F
17. The median of a density curve is the point that divides
the area under the curve in half..
T
F
18. The mean of a density curve is the point at which the
curve would balance if made of solid material.
T
F
19. The median of a skewed curve is pulled away from the
mean in the direction of the long tail.
T
F
20. All Normal curves have the same overall shape:
symmetric, unimodal and bell-shaped.
T
F
21. A Normal curve can be described completely by its
median and standard deviation.
T
F
22. The points at which the change in curvature takes
place are located at a distance of one standard
deviation on either side of the mean.
T
F
23. N(10, 2) describes a Normal distribution with a
standard deviation of 10 and a mean of 2.
T
F
24. Normal distributions are good descriptions for some
distributions of real data.
T
F
25. Many statistical inference procedures are based on
Normal distributions.
T
F
26. In a Normal distribution approximately 68% of the
observation fall within two standard deviation.
T
F
27. The 58-95-99.7 rule is sometimes called the Imperial
Rule
T
F
28. All models are wrong, and all are useful.
T
F
29. N(0, 1) is the standard Normal distribution.
T
F
30. Any question about what proportion of observations
lies in some range of values can be answered by
finding an area under the curve.
T
F
31. Always sketch the standard Normal curve, mark the zvalue and shade the area of interest.
T
F
32. To find area under the Normal distribution, you must
use the table in the back of the book.
T
F
If False, make a correct statement
2.2B:
Pages 118 – 120
Statement
T or F
33. You should always answer the question with a
complete sentence.
T
F
34. Using technology, you can find values from a given
area.
T
F
2.2C:
If False, make a correct statement
Pages 121 – 125
Statement
35. A Normality probability plot provides a good
assessment of whether a data set follows a Normal
distribution.
36. Even a small wiggle in a Normal probability plot is
enough information to determine a distribution is not
Normal.
37. If the points on a Normal probability plot lie close to a
straight line, the data are approximately Normally
distributed.
T or F
T
F
T
F
T
F
If False, make a correct statement
The Practice of Statistics – Chapter 3 Reading
3.1A:
Pages 142 – 149
Statement
T or F
1.
A response variable measures an outcome of a study.
T
F
2.
An explanatory variable may help explain or predict
changes in a response variable.
T
F
3.
A scatterplot show the relationship between two
quantitative variables measured on different
individuals.
T
F
4.
Always plot the response variable on the horizontal
axis of a scatterplot.
T
F
5.
You can describe the overall pattern of a scatterplot
by the direction, form and strength.
T
F
6.
An important kind of departure is an outlier, a value
that falls outside the overall pattern of the
relationship.
Two variables have a negative association when
above-average values of one tend to accompany
above-average values of the other.
T
F
T
F
7.
3.1B:
If False, make a correct statement
Pages 150 – 157
Statement
T or F
8.
Our eyes are good judges of how strong a linear
relationship is.
T
F
9.
The correlation measures the direction and strength of
the linear relationship between two quantitative
variables.
T
F
10. The letter “c” is used as the symbol representing
correlation.
T
F
11. Correlation is always a number between 0 and 1
T
F
12. A correlation value of 0 indicate a very weak linear
relationship.
T
F
13. Use a calculator to find the correlation coefficient.
T
F
14. Correlation makes a distinction between explanatory
and response variable. If you switch the two variables
you will get a different correlation.
T
F
15. The correlation does not change when we change the
units of measure of x, y, or both
T
F
16. The correlation is measured in the units of the
explanatory variable.
T
F
If False, make a correct statement
17. Correlation does not imply causation.
T
F
18. Correlation works for both quantitative and
categorical variable.
T
F
19. Correlation only explains the linear relationship
between two variables.
T
F
20. A value of r close to 1 or -1 guarantee a linear
relationship between two variable.
T
F
21. The correlation is strongly affected by an outlier
T
F
22. Correlation is a complete summary of two-variable
data.
T
F
3.2A:
Pages 164 – 168
Statement
T or F
23. A regression line is a line that describes how a
response variable x changes as an explanatory variable
y changes.
T
F
24. A regression line is a model to describe a relationship.
T
F
25. 𝑦̂ is the symbol use for the predicted value
T
F
26. The slope is the amount by which x is predicted to
change when y increases by one unit.
T
F
27. The y-intercept is the predicted value of y when x = 0.
T
F
28. The y– intercept is meaningful for all explanatory
variables.
T
F
29. You can determine how strong a relationship is by
looking at the size of the slope of the regression line.
T
F
30. Extrapolation is the use of a regression line for
prediction far outside the interval of values of the
explanatory variable x used to obtain the line
T
F
31. Extrapolated values of often accurate.
T
F
3.2B:
If False, make a correct statement
Pages 168 – 176
Statement
T or F
32. A good regression line makes the horizontal deviation
of the points from the line as small as possible.
T
F
33. A residual is the vertical difference between an
observed value of the response variable and the value
predicted by the regression line.
T
F
If False, make a correct statement
34.
T
F
35.
T
F
36.
T
F
37.
T
F
38.
T
F
39.
T
F
40.
T
F
41.
T
F
42.
T
F
43.
T
F
44.
T
F
45.
T
F
46.
T
F
47.
T
F
48.
T
F
49.
T
F
3.2C:
Pages 177 – 180
Statement
T or F
50.
T
F
51.
T
F
52.
T
F
If False, make a correct statement
53.
T
F
54.
T
F
55.
T
F
56.
T
F
57.
T
F
58.
T
F
59.
T
F
60.
T
F
61.
T
F
62.
T
F
63.
T
F
64.
T
F
65.
T
F
66.
T
F
67.
T
F
3.2D:
Pages 181 – 191
Statement
T or F
68.
T
F
69.
T
F
70.
T
F
71.
T
F
If False, make a correct statement
72.
T
F
73.
T
F
74.
T
F
75.
T
F
76.
T
F
77.
T
F
78.
T
F
79.
T
F
80.
T
F
81.
T
F
82.
T
F
83.
T
F
84.
T
F
85.
T
F