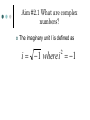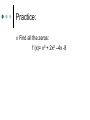* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Polynomial and Rational Functions
Survey
Document related concepts
Transcript
Polynomial and Rational Functions Aim #2.1 What are complex numbers? The imaginary unit I is defined as i 1 where i 1 2 Complex numbers and Imaginary Numbers The set of all numbers in the form of a + bi, with real numbers a and b and i, the imaginary unit, is called the set of complex numbers. An imaginary number in the form of bi is called a pure imaginary number. Example: -4 + 6i, 0+ 2i= 2i A complex number is said to be simplified if its in the form of a + bi. If b contain a radical express i before the radical. Equality of Complex numbers: a + bi= c + di if and only if a = c and b = d Operations with Complex Numbers (5 – 11i) + (7 + 4i) 1. 2. 3. Steps: Add or subtract the real parts Add or subtract the imaginary parts Express final answer as a complex number Operations with Complex Numbers (-5 + i) – (-11 – 6 i) 1. 2. 3. Steps: Add or subtract the real parts Add or subtract the imaginary parts Express final answer as a complex number Multiplying Complex Numbers 4i(3- 5i) Distribute 4i throughout the parenthesis Multiply Replace i2 with -1. Simplify Multiplying Complex Numbers (7 - 3i)(-2- 5i) Use the Foil Method or Vertical Method to multiply Replace i2 with -1 Simplify What are Conjugates? The complex conjugate of the number a + bi is a – bi and vice versa. When you multiply a complex number by its conjugate you get a real number. Using Complex Conjugates Divide and express the result in standard form. 7 4i 2 5i Multiply the numerator and denominator by the denominators conjugate. Use FOIL (or the Vertical Method) Replace i2 with -1 Simplify Express final answer in standard form. Roots of Negative Numbers Roots of Negative Numbers Perform the indicated operation. a. 18 8 b.(1 5 ) 2 25 50 c. 15 Summary: Answer in complete sentences. What is i? Explain how to add or subtract complex numbers. What is the conjugate of a complex number? Explain how to divide complex numbers and provide an example. Aim #2.2: What are some properties of quadratic functions? The Standard Form of Quadratic Function: f ( x ) a ( x h) k where (h, k ) is the vertex if a 0 opens upward if a 0 opens downward 2 General Form of a Quadratic: f (x)= ax2 + bx + c To find the vertex using this form you need the axis of symmetry: b x 2a Graphing a Quadratic Function 1. 2. 3. 4. 5. Identify which way the parabola will open Identify the vertex Find the y –intercept by evaluating f(0). Find the x-intercepts. Then graph. Converting from General to Standard Form Convert the function: Y = x2 + 4x – 1 Steps: Practice: Convert to standard form. Y = 3x2 + 6 x + 7 Summary: Answer in complete sentences. 3- List three things you learned about quadratic functions. 2- List 2 ways you can apply this to real world. 1- Write one question that you may still have on this topic. Aim #2.3: How do we identify polynomial functions and their graphs? Examples and Non examples: Definition of a Polynomial Function Smooth, Continuous Graphs Polynomial functions of degree 2 or higher have graphs that are smooth and continuous. Leading Coefficient Test Use the leading coefficient test to determine the end behavior. f (x)= x3 + 3x2 – x - 3 End behavior is how we describe a graph to the far left or far right. Using the Test: The leading coefficient is 1. The exponent is odd Odd-degree have graphs with opposite behavior at each end. Leading Coefficient Test Odd – degree; positive leading coefficient Graphs falls left and increases right Odd – degree; negative leading coefficient Graph rises left and falls right Guided Practice: Use the leading coefficient test to determine the end behavior. f (x)= x4 – 4x2 Even degree; positive leading coefficient Rises left and rises right Even degree; negative leading coefficient Falls left and falls right Using the Leading Coefficient Test Use the leading coefficient test to determine the end behavior of the graph of: f (x) = -4x3 ( x -1)2 (x + 5) Zeros of Polynomial Functions Find all the zeros: f (x)= x3 + 3x2 –x -3 Practice: Find all the zeros: f (x)= x3 + 2x2 –4x -8 Finding Zeros of a Polynomial Function Find all the zeros: f (x)= - x4 + 4x3 – 4x2 Steps: Set f (x) = 0 Multiply both sides by -1. Factor the GCF. Factor completely. Solve for x. Multiplicities of Zero Multiplicity and X-intercepts If r is a zero with even multiplicity, then the graph touches the x-axis and turns around at r. Multiplicity and X-intercepts If r is a zero with odd multiplicity, then the graph crosses the x-axis at r. Note: Regardless of multiplicity graphs tend to flatten out near the zeros with multiplicity greater than one. Finding Zeros and their Multiplicities Find the zeros of f (x)= ½ (x + 1) (2x – 3)2 and give the multiplicity of each zero. State whether the graph crosses the x-axis or touches the x-axis and turns around at each zero. Steps: 1. Set f (x)= 0 and set each variable factor to 0. Aim # 2.4 How do we divide polynomials? Guided Practice: The Remainder Theorem The Factor Theorem Practice: Summary: Answer in complete sentences. Aim #2.5: How do we find the zeros of a polynomial function? Rational Zero Theorem provides us with a tool we can use to make a list of all possible rational zeros of a polynomial function. Theorem states: Factors of the cons tan t Possible rational zeros Factors of the leading coeffient Ex 1: Using the Rational Zero Theorem Ex. 1 Continued Now we need to take each number in the 1st row and divide by each number in the second row. How many possible rational zeros are there? Practice: List all the possible rational zeros of: f ( x) x 2 x 5 x 6 3 2 Ex. 2 Using the Rational Zero Theorem Ex. 3 Finding the Zeros of a Polynomial Function Part 2 Watch the video: On finding the Zeros sing the Rational Zero Theorem. Copy the link into your browser or go to my web page and click http://brightstorm.com/math/precalculus/ polynomial-and-rationalfunctions/finding-zeros-of-apolynomial-function// Summary: Answer in complete sentences. Explain how to generate possible solutions to a polynomial function. Explain how we use the process of trial and error and synthetic division to find the actual zeros of the polynomial function. Aim #2.6: How do we find the asymptotes of a rational function? Key Terms: Rational Function Domain Vertical Asymptotes Horizontal Asymptotes Slant or Oblique Asymptotes If you were absent from class- watch the videos on my web page on horizontal and slant asymptotes. In addition, check a classmates notes. Summary: Answer in complete sentences. What are the different types of asymptotes? Explain how to locate the different types of asymptotes. Be sure to include examples for each type to illustrate your explanation.