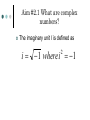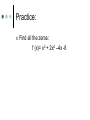Download Polynomial and Rational Functions

Polynomial and
Rational Functions
Aim #2.1 What are complex
numbers?

The imaginary unit I is defined as
i   1 where i  1
2
Complex numbers and
Imaginary Numbers

The set of all numbers in the form of a + bi,
with real numbers a and b and i, the
imaginary unit, is called the set of
complex numbers.
An imaginary number in the form of bi is
called a pure imaginary number.
 Example: -4 + 6i, 0+ 2i= 2i

A complex number is said to be
simplified if its in the form of a + bi.
 If b contain a radical express i before
the radical.


Equality of Complex numbers:
a + bi= c + di
if and only if a = c and b = d
Operations with
Complex Numbers

(5 – 11i) + (7 + 4i)

1.
2.
3.
Steps:
Add or subtract the real
parts
Add or subtract the
imaginary parts
Express final answer as
a complex number
Operations with
Complex Numbers

(-5 + i) – (-11 – 6 i)

1.
2.
3.
Steps:
Add or subtract the real
parts
Add or subtract the
imaginary parts
Express final answer as
a complex number
Multiplying
Complex Numbers

4i(3- 5i)




Distribute 4i throughout
the parenthesis
Multiply
Replace i2 with -1.
Simplify
Multiplying
Complex Numbers

(7 - 3i)(-2- 5i)



Use the Foil Method or
Vertical Method to
multiply
Replace i2 with -1
Simplify
What are Conjugates?
The complex conjugate of the
number a + bi is a – bi and vice
versa.
 When you multiply a complex number
by its conjugate you get a real
number.

Using Complex
Conjugates

Divide and express
the result in standard
form.
7  4i
2  5i





Multiply the numerator
and denominator by the
denominators conjugate.
Use FOIL (or the Vertical
Method)
Replace i2 with -1
Simplify
Express final answer in
standard form.
Roots of Negative Numbers
Roots of Negative Numbers

Perform the indicated operation.
a.  18   8
b.(1  5 )
2
 25   50
c.
15
Summary:
Answer in complete sentences.
What is i?
 Explain how to add or subtract
complex numbers.
 What is the conjugate of a complex
number?
 Explain how to divide complex
numbers and provide an example.

Aim #2.2: What are some
properties of quadratic functions?

The Standard Form of Quadratic
Function:
f ( x )  a ( x  h)  k
where (h, k ) is the vertex
if a  0 opens upward
if a  0 opens downward
2
General Form of a Quadratic:
 f (x)= ax2 + bx + c
 To find the vertex using this form you
need the axis of symmetry:

b
x
2a
Graphing a Quadratic Function
1.
2.
3.
4.
5.
Identify which way the parabola will
open
Identify the vertex
Find the y –intercept by evaluating
f(0).
Find the x-intercepts.
Then graph.
Converting from
General to Standard Form
Convert the function:
 Y = x2 + 4x – 1

Steps:

Practice:

Convert to standard form.
Y = 3x2 + 6 x + 7
Summary:
Answer in complete sentences.
3- List three things you learned about
quadratic functions.
2- List 2 ways you can apply this to real
world.
1- Write one question that you may still
have on this topic.
Aim #2.3: How do we identify
polynomial functions and their
graphs?

Examples and Non examples:
Definition of a Polynomial
Function
Smooth, Continuous Graphs

Polynomial functions of degree 2 or
higher have graphs that are smooth
and continuous.
Leading Coefficient Test


Use the leading
coefficient test to
determine the end
behavior.
f (x)= x3 + 3x2 – x - 3

End behavior is how we
describe a graph to the far
left or far right.
Using the Test:
The leading coefficient is 1.
The exponent is odd
Odd-degree have graphs with
opposite behavior at each
end.

Leading Coefficient Test
Odd – degree; positive leading
coefficient
 Graphs falls left and increases right


Odd – degree; negative leading
coefficient
 Graph rises left and falls right
Guided Practice:


Use the leading
coefficient test to
determine the end
behavior.
f (x)= x4 – 4x2
Even degree; positive
leading coefficient
Rises left and rises right
 Even degree; negative
leading coefficient
Falls left and falls right

Using the
Leading
Coefficient Test

Use the leading coefficient test to determine
the end behavior of the graph of:
 f (x) = -4x3 ( x -1)2 (x + 5)
Zeros of Polynomial
Functions

Find all the zeros:
f (x)= x3 + 3x2 –x -3
Practice:

Find all the zeros:
f (x)= x3 + 2x2 –4x -8
Finding Zeros of a
Polynomial Function

Find all the zeros:
f (x)= - x4 + 4x3 – 4x2






Steps:
Set f (x) = 0
Multiply both sides by -1.
Factor the GCF.
Factor completely.
Solve for x.
Multiplicities of Zero
Multiplicity and X-intercepts

If r is a zero with
even multiplicity,
then the graph
touches the x-axis
and turns around
at r.
Multiplicity and X-intercepts

If r is a zero with odd multiplicity, then
the graph crosses the x-axis at r.

Note: Regardless of multiplicity
graphs tend to flatten out near the
zeros with multiplicity greater than
one.
Finding Zeros and their
Multiplicities
Find the zeros of f (x)= ½ (x + 1) (2x – 3)2
and give the multiplicity of each zero.
 State whether the graph crosses the x-axis
or touches the x-axis and turns around at
each zero.

Steps:
1. Set f (x)= 0 and set each variable factor to 0.

Aim # 2.4 How do we divide
polynomials?
Guided Practice:
The Remainder Theorem
The Factor Theorem
Practice:
Summary:
Answer in complete sentences.
Aim #2.5: How do we find the
zeros of a polynomial function?

Rational Zero Theorem provides us with a
tool we can use to make a list of all
possible rational zeros of a polynomial
function.
Theorem states:
Factors of the cons tan t
Possible rational zeros 
Factors of the leading coeffient
Ex 1: Using the Rational Zero
Theorem
Ex. 1 Continued
Now we need to take each number in
the 1st row and divide by each number
in the second row.
 How many possible rational zeros are
there?

Practice:

List all the possible rational zeros of:
f ( x)  x  2 x  5 x  6
3
2
Ex. 2 Using the Rational Zero
Theorem
Ex. 3 Finding the Zeros of a
Polynomial Function
Part 2
Watch the video: On finding the Zeros
sing the Rational Zero Theorem.
Copy the link into your browser or go to
my web page and click
http://brightstorm.com/math/precalculus/
polynomial-and-rationalfunctions/finding-zeros-of-apolynomial-function//
Summary:
Answer in complete sentences.
Explain how to generate possible
solutions to a polynomial function.
 Explain how we use the process of
trial and error and synthetic division to
find the actual zeros of the polynomial
function.

Aim #2.6: How do we find the
asymptotes of a rational function?








Key Terms:
Rational Function
Domain
Vertical Asymptotes
Horizontal Asymptotes
Slant or Oblique Asymptotes
If you were absent from class- watch the videos on my web
page on horizontal and slant asymptotes.
In addition, check a classmates notes.
Summary:
Answer in complete sentences.
What are the different types of
asymptotes?
 Explain how to locate the different
types of asymptotes. Be sure to
include examples for each type to
illustrate your explanation.
