Download Review-QM`s and Density of States

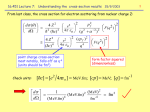
Review-QM’s and Density of States
Last time, we used a quantum mechanical, kinetic model,
and solved the Schrodinger Equation for an electron in a 1-D
box.
nx 

-(x) = standing wave = x  Asin 
 L 
Extend to 3-D and use Bloch Function to impose periodicity to
boundary conditions 
-(x) = traveling wave =  k r   exp ik r 
2
2
2
2
2
2
k x  0,
L
,4
L
,...k y  0,
L
,4
L
,...k z  0,
We showed that this satisfies periodicity.

ik a
-  r  a  e  r    r 

L
,4
L
,...
Review-QM’s and Density of States
Plug into H = E to find energy.
k 
2
2m
k2 
2
2m
2
2
2
k

k

k
 x y z
Since k, higher energy corresponds to larger k.
For kFx=kFy=kFz (i.e. at the Fermi Wave Vector), the Fermi

Surface (surface of constant energy, wave vector,
temperature) the is a shpere. This applies to valence band
for Si, Ge, GaAs; and couduction band for GaAs.
F 
2
2m
k F2
< F, filled states

> F, empty states
Fermi Surfaces in Real Materials
If kxF≠kFy≠kFz, then you get constant energy ellipsoids. Also, if
k=0 is not lowest energy state, (e.g. for pz orbitals where k= is
the lowest energy), you don’t get a constant energy sphere.
e.g. Silicon and Germanium
CB energy min occurs at
Si - X point, k= along <100> directions
Ge - L point, k= along <111> directions
Review-QM’s and Density of States
3
4

k
volume_ of _ sphere
F
3

# of states in sphere =
volume_ of _1_ state 2 3
 
 L 
# of electrons = 2x Number of states, because of spin
degeneracy (2 electrons per state)
2
 V
 2m
L3  V
N
3
3
k
2 F
F 
2m
k F2
kF 
F
2
Now we wish to calculate density of states by differentiating N
with respect to energy


V 2m 3 2
dN
D 
 2 
d 2 
2
 

1
2
Review-QM’s and Density of States
3
1
1 2m  2
D 
 2  E  E C  2
2 

*
e
3
1
1 2m  2
D 
 2  E V  E  2
2 

*
e
Number of electrons, n, can be calculated at a given T
by integration.
n

 Df d
B.E.
Review-QM’s and Density of States
 EC  E F  
n  NC exp
kT


m kT  2
NC  2
2 
2



 E F  EV  
p  NV exp
kT


m*h kT  2
Eff. DOS VB
NV  2
2 
2 

*
e
3
Eff. DOS CB
3
We can now calculate the n,p product by multiplying
the above equations.
E g 

np  n
np  NC NV exp

2
i =(intrinsic
carrier concentration)2
For no doping and no electric fields

n  p  ni 
kT

E g

NC NV exp

2kT


Add
 a field and n≠p, but np=constant
Outline - Moving On
1. Finish up Si Crystal without doping
2. Talk about effective mass, m*
3. Talk about doping
4. Charge Conduction in semiconductors
Intrinsic Semiconductors
It is useful to define the “intrinsic Fermi-Level”, what you get
for undoped materials. (EF(undoped) = Ei, n=p=ni)
 E C  E i  
 E i  E V  
NC exp
 NC exp

kT
kT



NV 
E i  EC EV  E i

 ln  
kT
kT
NC 
NV 
E i  E C  E V  E i  kTln  
NC 
NV 
2E i  E C  E V  kT ln  
NC 
NV 
2E i  E V   E C  E V  kT ln  
NC 
Intrinsic Semiconductors
E i  EV  
Eg
N 
V

kTln


2
NC 
m kT
2
2
NV


NC
m*e kT
2
2

*
h
kT NC 
ln  
2 NV 
Eg
Si
-13 meV
1.12 eV
Ge

GaAs
-7 meV
35 meV
0.67 eV
1.42 eV
3
 2
2 
m*h

3 
*
2
m

e
2 

The energy offset from the center of the band
gap is in magnitude compared to the magnitude
of the bandgap.
REMEMBER: There are no states at Ei or EF.
They are simply electrochemical potentials that
give and average electron energy
Intrinsic Semiconductors
m kT
2
2
NV


NC
m*e kT
2
2

*
h
E i  EV 
Eg
3
 2
2 
m*h

3 
*
 2 me
2 

*


m
3
h

kTln
* 
2
4
 me 

For Si and Ge, me* > mh*, so ln term < 0, Ei < Eg
For GaAs, me* < mh*, so ln term < 0, Ei < Eg


Effective Mass
The text book 3.2.4 derives m* from QM treatment of a wave
packet.
m* 
2
d E 


 dk 
2
(This expression can be derived
quantum mechanically for a
wavepacket with group velocity vg)
We can use this quantum mechanical results in Newtonian
physics. (i.e. Newton’s Secone Law)
2
dv g
F 2
 m*
 m*a
d E 
dt
 2 
dk 
Thus, electrons in crystals can be treated like “billiard balls”
in a semi-classical sense, where crystal forces and QM
properties
 are accounted for in the effective mass.
Effective Mass
2
1
1 d 2 E 
1
1 d E k 
 2  2  or
 2 



m*
mij *
dk
dk
dk 
 i j 
So, we see that the effective mass is inversely related to the
band curvature. Furthermore, the effective mass depends on
which direction in k-space we are “looking”

1
m*de  m1* m*2 m*3  3
In silicon, for example
m  m m
*
de
*
l
*
t

1
3
Where ml
* is the effective mass along the longitudinal
direction of the ellispoids and mt* is the effective mass along
the transverse direction of the ellipsoids

Effective Mass
Relative sizes of ml* and mt* are important (ultimately leading
to anisotropy in the conductivity)
2


m
length _ of _ ellipsoid _ along _ axis
 

m max_ width _ of _ ellipsoid _ perpendicular _ to_ axis 
*
l
*
t
2
1
1 d 2 E 
1
1 d E k 
 2  2  or
 2 



m*
mij *
dk
dk
dk 
 i j 
Again, we stress that effective
mass is inversly proportional to
band curvature. This means that

for negative curvature,a particle
will have negative mass and
accelerate in the direction opposite
to what is expected purely from
classical considerations.
Effective Mass
One way to measure the effective mass is cyclotron resonance v. crystallographic
direction.
-We measure the absorption of radio frequency energy v. magnetic field
strength.
c 
qB
m*
Put the sample in a microwave resonance cavity at 40 K and adjust the rf
frequency until it matches the cyclotron frequency. At this point we see a resonant
peak in the energy absorption.
Carrier Statistics inDoping
Semiconductors
-Replace Si lattice atoms with
another atom, particularly with
an extra or deficient valency.
(e.g. P, As, S, B in Si)
 D  EC  ED
εD is important because it tells you what
fraction of the dopant atoms are going
to be ionized at a given temperature.
For P in Si, εD = 45 meV, leading to
99.6% ionization at RT.
Then, the total electron concentration
(for and n type dopant) is
n  ni  N

D
Carrier Statistics in Semiconductors
If we look at the Fermi Level position as a
function of temperature (for some
sample), we see that all donor states are
filled at T = 0 (n ≈ 0, no free carriers), EF
= ED. At high temperatures, such that, ni
>> ND, then n ≈ ni and EF ≈ Ei.
EF ranges between these limiting values
at intermediate temperatures. (see fig)
Np=ni2 still holds, but one must substitute
n = ni + ND+ p = ni2/(ni + ND+).
At room temperature n ≈ ND+
For Silicon
- ni = 1010 cm-3.
- ND = 1013 → 1016 cm-3
(lightly doped → heavily doped)
Carrier Statistics in Semiconductors
n  NC
E  EF 
exp   C


kT 
n
1016
E  E F  
 19  exp  C
kT 

N D 10
This is 60meV/decade. Three decades x 60 meV/decade = 180 meV = EC – EF. EF
is very close to the conduction band edge.
Similar to EF(T), let’s look at n(T)
Charge Conduction in
KE  1 mevth2
Semiconductors
1-D
2
KE  3 kT
2
3-D (from Statistical Mechanics)
Brownian Motion
Applying a force to the particle directionalizes the
net movement. The force is necessary since
Brownian motion does not direct net current.
F   qE  me*a
q < 0 for e-, q > 0 for h+
Constant Field leads to an acceleration of carriers scaled by me*.
If this were strictly true, e-’s would
accelerate without bound under a
constant field. Obviously, this isn’t the
case. Electrons are slowed by scattering
events.
Scattering Processes in Semiconductors
1) Ionized Impurity Scattering
2) Phonon (lattice) Scattering
3) Neutral Impurity Scattering
4) Carrier-Carrier Scattering
5)Piezoelectric Scattering
Scattering Processes in Semiconductors
3) - Donors and acceptors under freez-out.
- Low T only
- Defect = polycrystalline Si
4) - e- - h+ scattering is insignificant due to low carrier concentration of one type or
another
- e- - e- or h+ - h+ don’t change mobility since collisions between these don’t
change the total momentum of those carriers.
5) - GaAs: displacement of atoms → internal electric field, but very weak.
2) - collisions between carriers and thermally agitated lattice
atoms. Acoustic
5
3
2
2
 ~ m*
T
- Mobility decreases as temperature increases due to
increased lattice vibration
- Mobility decreases as effective mass increases.
Scattering Processes in Semiconductors
1) Coloumb attraction or repulsion between charge carriers and ND+ or NA-.
5
 ~ m*
2
T
3
2
Due to all of these scattering processes, it is possible to define a mean free time,
m, and a mean free path lm.
F   qE  me*a
Average directed velocity
 a  t  a m
vavg . _ drift  a me
q m , e E
vdrift  
me*
q m , e
 *
me
a
qE
me*
vd   e E
 e   m ,e
e  1
me*
For solar cells (and most devices) high mobility is desirable since you must apply
a smaller electric field to move carriers at a give velocity.
Current Flow in Semiconductors
e-
(cm-3)(cm/s) = e-/cm-2 s
flux  nvd
J  current _ density
A/cm-2 = C/cm-2 s
J   qnvd
J  qnn E
J  E
  conductivity  qnn
 n
  n
For Holes
Total
Resistance
n-type
Current Flow in
Semiconductors
  qp
h
  qn p  qph
1
1
 
 qn n   p p 

1
qn N D
n  ND
n n   p p
Mobility
Mobility
Saturation Velocity
Mobility and Impurities