Download April 27 - probably will be discussed only briefly

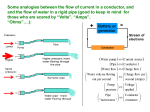
Some analogies between the flow of current in a conductor, and
and the flow of water in a rigid pipe (good to keep in mind for
those who are scared by “Volts”, “Amps”,
“Ohms”….):
+
Battery or
generator
-
Stream of
electrons
Conductor
Water pump   Current source 
Pipe   Conductor 
Water flow   Charge flow 
 Water volu me flowing   Charge flow per 

  

out
per
second
second
(Amps)

 

 Pump   Voltage 

  

pressure
applied

 

Pipe

  Conductor 

  

"
narrowness
"
resistance

 

One more thing to remember:
Note: this is also true for any current source. Current
not only flows out of a battery – exactly the same
amount of charge returns by the other terminal.
Electrical conductivity: let’s begin with metals, which are the
relatively simple conductors.
Electrons in a metal occupy quantum states. There are
many states with different energies. We can imagine such states
as “parking sites” in a multi-level parking garage.
Note the analogy with H2O
molecules in a glass of water:
Two cars cannot
occupy the same
site.
Likewise, two
electrons cannot
occupy the same
quantum state.
So, the electrons
occupy available
states with the
lowest energies,
up to certain level –
and all states above
are “empty” .
As we said, all conductors have to obey the rule:
“one electron in, one out”. Our “garage” obeys
an analogous rule: one car in, one car out.
The “garage” is a good “car conductor”, because
the cars can move freely at the level that is not
occupied:
In semiconductors, the situation is different:
Just above the filled levels, there are several
levels that are not accessible. It’s an analogy
with the famous energy gap in semiconductors.
The cars could
move freely at
the levels above
the “forbidden
zone” – however,
there is no such
an elevator that
could move them
up there.
However, if additional containers with cars are placed
In the “forbidden zone” near its top, then the cars
can be easily lifted to the “allowed levels” above, and
“car traffic” in our garage becomes possible.
In real semiconductors,
atoms that have one
loosely coupled electron
may be put near the top
of the energy gap, an
they may “donate”
the electron to levels
above the energy
gap, where they can
move freely. Such atoms
are called “donor atoms”,
and such semiconductors
ale called n-type or
n-doped .
However, there is another possible way of enabling the cars to
move. We can put special “containers” near the bottom of the
“forbidden zone” – each container can “capture” a car from
the level underneath, leaving a vacant space, a hole.
In real semiconductors
atoms that can absorb
an extra electron are
put near the energy
gap bottom. Such
atoms are called
acceptors, and the
vacant electron
states they create
are called holes.
Such semiconductors
are called p-type or
p-doped.
Once a “hole” is created, the cars may start moving!
One by one, the cars shift to the left by one position,
and thus the hole “propagates” to the right, until it
reaches the rightmost space – as is shown in this
animation:
(the animation is repeated five times, and the stops).
Once the hole moved all the way to the right, a car from outside
can move into the vacant space. But due to the “one in, one
out” rule, the leftmost car has to leave the garage.
It creates a new hole which again propagates all the
way to the right, and the cycle is repeated. Cars keep moving in
and out of the garage!
COCLUSIONS FROM THE LAST SEVERAL SLIDES:
Free electrons in metals and n-type semiconductors are
negative current carriers.
The holes in p-type semiconductors behave as positive current
carriers.
Now we are almost ready to start talking about p-n
junctions, which are the crucial elements of solar
cells.
But before we start, let’s refresh our memory about
the electric potential.
But first a few words about the potential due to
Earth gravity:
m
m
mg
m
h1
U1 = mgh1
m
mg
h2
U2 = mgh2
Earth surface
The measure of the potential due to gravity
is the potential energy of a unit mass in a
gravitatio nal field : V  g  h
Bodies always move toward a lower potential.
If there were " anti - mass" repelled by Earth,
such bodies would, conversly, move toward
a higher potential (like baloons). But there is
no gravitatio nal repulsion.
Electric charges are sources of electric fields.
The electric field can also be described in terms
of the potential.
The measure of the potential of an electric field
is the potential energy of a unit positive charge
placed in this field.
A simple-minded theory of a p-n junction
Taka a piece of p-type silicon, and a piece of n-type silicon. In each
there are mobile carriers -- holes and electrons, respectively. The
donor and acceptor atoms are not mobile! They are solidly built in
the crystal structure
of silicon.
But both materials
are electrically neutral,
because in each the
charge of the mobile
carriers is compensated
by the charge acquired
by the donor/acceptor
atoms.
When p and n-type semiconductors are combined, they
form a p-n junction. Mobile carriers from each side
diffuse across the “borderline”….
Extra
Extra
negative positive
charge
charge
Consider a large (“semi-infinite”) slab with uniform negative
volume charge. A positive point charge Q located outside the
slab is always attracted toward it with the same force, regardless
of the distance to the slab surface.
Uniform
negative
charge
And what if the charge is inside the slab? Then we can always
Divide the slab in our mind into two “sub-slabs”, of which one
Pulls the charge to the left, and the other one to the right, with
forces proportional to the amount
of charge in each imaginary “subslab”. Hence, a plot of the force
acting on the charge Q as a function of its position looks as
plotted below:
F
-d/2
d
d/2
x
Let’s now take two slabs of the same thickness d and with volume
charges of the same
density, but opposite
signs.
Force from the
negative slab
F
-d
Force from the
positive slab
+
d
x
Force from the
negative slab
F
11
-d
0
Force from the
positive slab
d
x
-1
Net force from
both slabs
0
-2
x
Conclusion: we now
understand where this
graph comes from!
The force acting on a
positive charge in the
“space charge” region
is always negative (i.e.,
to the left) and has the
form of a “dip”.
Conversely, a negative
charge is always driven
to the right.
To reach the overall
conclusion, we have
to say a few words
about the Photoelectric
Effect .