Download SAT Verbal

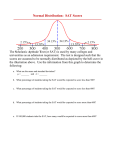
Math 116 - SAT VERBAL SCORES
Chapter 7.2 – Distribution of Sample Means
2) The mean SAT verbal score of students whose first language is English is 515, on the basis of data
obtained from the College Board. SAT verbal scores are normally distributed with a population standard
deviation of 112.
a) Give the shape, mean and standard deviation of the distribution of sample means for samples of size
20.
Notice: the population is all students who have taken the SAT verbal exam whose first language is
English, and the variable X is the SAT verbal score
X is Normal with   515 and   112
According to the Central Limit Theorem, the distribution of sample means is normal for any
sample size because X is normally distributed. Hence, for samples of size 20, the distribution of xbar is also normal with
 x    515
x 

n

112
 25.04
20
b) What is the probability that a sample of size 20 has a mean of at most 458?
P( x  458)  P( z 
458  515
)  P( z  2.28)  0.0113
112
20
With calculator: normalcdf(-109 ,458,515,
112
1
) = 0.0114~0.01=
100
20
c) The probability of observing a sample of size 20 with a mean of 458 or less when the population
mean is 515 is 0.01_______.
So, for samples of size 20, about __1____ sample(s) in 100 will result in a sample mean of 458 or less
when the population mean is 515.
Because this event only happens __1___ out of __100___ times, we consider it to be unusual.
d) What may this result suggest?
A mean score of 458 is unusually low (the probability of observing a 458 or lower is less than 0.05).
When the population mean is 515, there is a very small probability of getting a
sample mean of 458 or lower when 20 scores are randomly selected.
If the mean of the population is actually 515, a rare event has happened, OR the small probability
may suggest that the mean of the population from which the sample was selected is lower than 515
(because such a sample mean is more likely when the mean is lower than 515).
If the population mean is 515, it’s very unusual to observe a sample of size 20 with a mean of 458
or less. *******This unusually low result may suggest that “probably” the sample was selected
from a population with mean lower than 515.