Download AP Statistics Review 1, Chapters 6 to 8 6.79 Are you my Blood Type

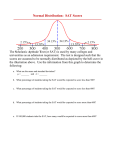
AP Statistics
Review 1, Chapters 6 to 8
6.79 Are you my Blood Type? All human blood can be “ABO-typed” as one of O, A, B, or AB, but the
distribution of the types varies a bit among groups of people. Here is the distribution of blood types for a
randomly chosen person in the United States:
Blood Type
US Probability
O
.45
A
.40
B
.11
AB
?
a) What is the probability of type AB blood in the US?
b) An individual with type B blood can safely receive transfusions only from persons with type B or type O
blood. What is the probability that the husband of a woman with type B blood is an acceptable blood
donor for her?
c) What is the probability that in a randomly chosen couple the wife has type B blood and the husband has
type A?
d) What is the probability that one of a randomly chosen couple has type A blood and the other has type B?
6.80 The distribution of blood types in China differs from the US distribution given previously. In China, the
distribution is
Blood type
China Probability
O
.35
A
.27
B
.26
AB
.12
Choose an American and a Chinese at random, independently of each other.
a) What is the probability that both have type O blood?
b) What is the probability that both have the same blood type?
7-8A. Which Setting: Determine if a binomial or a geometric setting is appropriate for each of the following:
a) Fifty students are taught about the empirical rule by a television program. After completing their study, all
students take the same examination. The number of students who pass is counted.
b) A statistician records the number of times a player makes both shots in a one-and-one foul-shooting situation.
(In this situation, the player gets to attempt a second shot only if he or she makes the first shot.)
c) A chemist repeats a solubility test 10 times on the same substance. Each test is conducted at a temperature
10o higher than the previous test. She counts the number of times that the substance dissolves completely.
d) Draw a card from a deck without looking, observe the card, and replace the card within the deck. Count the
number of times your draw a card in this manner until you observe a jack.
7A. SAT Scores: A college uses SAT scores as one criterion for admission. Experience has shown that the
distribution of SAT scores among its entire population of applicants is as follows:
(X) SAT Math scores are N(625, 90) and (Y) SAT Verbal scores are N(590, 100)
Let’s suppose that SAT Math and Verbal scores are independent (which is not accurate).
a) Find the mean and standard deviation of the difference in math and verbal score (X-Y) among the applicant
pool.
b) Find the probability that the math score is higher than the verbal score for a randomly chosen applicant.
8.8 Marital Status: Among employed women, 25% have never been married. Select 10 employed women at
random.
a) The number in your sample who have never been married has a binomial distribution. Describe X using
proper (shorthand) statistical notation.
b) What is the probability that exactly 2 of the 10 women in your sample have never been married. Use the
appropriate formula and show your work.
c) What is the probability that fewer than 4 have never been married?
8.39 Testing Hard Drives: Suppose we have data that suggests the 3% of a company’s hard drives are defective.
What is the probability that the first defective hard drive is found on the fifth unit tested?
What is the probability that it takes more than four units to find the first defective one?
8.30 Lie Detectors: A federal report finds that lies detector tests given to truthful persons have probability about
0.2 of suggesting that the person is deceptive.
a) A company asks 12 job applicants about thefts from previous employers, using a lie detector to assess their
truthfulness. Suppose that all 12 answer truthfully. What is the probability that the lie detector says all 12 are
truthful?
b) What is the probability that the lie detector says at least 1 is deceptive?
c) What is the mean number among 12 truthful persons who will be classified as deceptive? What is the
standard deviation of this number?
d) What is the probability that the number classified as deceptive is less than the mean?