* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Berry`s Phase
Bell's theorem wikipedia , lookup
Hidden variable theory wikipedia , lookup
Double-slit experiment wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Ultrafast laser spectroscopy wikipedia , lookup
Matter wave wikipedia , lookup
Ellipsometry wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Berry’s Phase in Single Mode
Optical Fiber
PHY 243W Advanced Lab
Chris McFarland
Ryan Pettibone
Emily Veit
Theory
• Berry’s Phase is a geometric phenomenon the
can manifest itself in optics, quantum mechanics
and even classical mechanics.
• It occurs when more than one physical
parameter of the particle’s path are changed
adiabatically.
• Although the parameters are returned to their
original values the measured quantity (spin or
polarization) does not.
• EXAMPLE: Two parameters characterizing an
EM wave could be the polar and azimuthal angle
of the wave’s propagation vector!
Manifestation of Theory
• As we all know {k,E,B} constitutes an
orthogonal basis.
• The optical fiber parallel transports the
basis.
• Linearly polarized light enters the optical
fiber in one direction, exits in same
direction, but plane of polarization is
different!
Ein
Eout
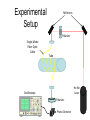
Experimental
Setup
Reflectors
Polarizer
Single-Mode
Fiber Optic
Cable
Tube
He-Ne
Laser
Oscilloscope
Polarizer
Photo-Detector
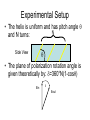
Experimental Setup
• The helix is uniform and has pitch angle
N
and N turns:
Side View
• The plane of polarization rotation angle is
given theoretically by: =360°N(1-cos)
Ein
Eout
Experimental Issues
We felt that there were two main sources of
error:
• The “Dandruff Effect:” Noise is created by
air currents and tiny dust particles blocking
the laser.
– SOLUTION: Create a tunnel around the laser
• Slack in the Cable: Berry’s phase can
occur in the optical fiber.
– SOLUTION: Lay the fiber flat
Experimental Issues
• not large enough to measure accurately
– SOLUTION: Increase N to amplify since is
proportional to N.
Results
Rotation Angle vs. Helical Angle
400
350
Rotation Angle
300
250
Our Data
Theory
200
150
100
50
0
0
10
20
30
40
50
60
70
Helical Angle (Degrees)
80
90
100
Results
Expected Phase Shift vs. Measured Phase Shift
400
Measured Phase Shift
350
y = 1.0084x - 5.9247
R2 = 0.9899
300
250
200
150
100
50
0
0
50
100
150
200
250
Expected Phase Shift (Degrees)
300
350
400
Conclusion
• Qualitatively observing the effect of Berry’s
phase by manipulation of the optical fiber was
relatively easy.
• However, the next group working on this should
be careful to eliminate aforementioned errors if
they wish to obtain results approximating
theoretical results.
• Our data matches the theoretical results closely,
providing strong evidence for the Berry’s phase
hypothesis.
ANY QUESTIONS??