* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Flux of an Electric Field - Erwin Sitompul
History of subatomic physics wikipedia , lookup
Electromagnetism wikipedia , lookup
Condensed matter physics wikipedia , lookup
Time in physics wikipedia , lookup
Maxwell's equations wikipedia , lookup
Lorentz force wikipedia , lookup
Chien-Shiung Wu wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Field (physics) wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
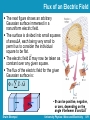
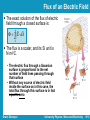
Lecture 8 Ch23. Finding the Electric Field – II University Physics: Waves and Electricity Dr.-Ing. Erwin Sitompul http://zitompul.wordpress.com 2013 Homework 6: Three Particles Three particles are fixed in place and have charges q1 = q2 = +p and q3 = +2p. Distance a = 6 μm. What are the magnitude and direction of the net electric field at point P due to the particles? p 1.602 1019 C e 1.602 1019 C Erwin Sitompul University Physics: Wave and Electricity 8/2 Solution of Homework 6: Three Particles EP ,net E1 E2 E3 E2 E3 E1 E1 E2 0 EP ,net E3 k EP ,net r3 P 12 aˆi 12 aˆj r3P 12 2a r rˆ3 P 3 P 12 2iˆ 12 2jˆ r3 P cos ˆi sin ˆj 45 Erwin Sitompul • Both fields cancel one another q3 r3 P r̂ 2 3P (2 1.602 1019 ) 8.99 10 1 ( 2 2(6 106 ))2 9 160 N C • Magnitude EP ,net 45 • Direction University Physics: Wave and Electricity 8/3 The Electric Field → The calculation of the electric field E can be simplified by using→symmetry to discard the perpendicular components of the dE vectors. For certain charge distributions involving symmetry, we can simplify even more by using a law called Gauss’ law, developed by German mathematician and physicist Carl Friedrich Gauss (1777–1855). → Instead of considering dE in a given charge distribution, Gauss’ law considers a hypothetical (imaginary) closed surface enclosing the charge distribution. Gauss’ law relates the electric fields at points on a closed Gaussian surface to the net charge enclosed by that surface. Erwin Sitompul University Physics: Wave and Electricity 8/4 Flux → Suppose that a wide airstream flows with uniform velocity v flows through a small square loop of area A. Let Φ represent the volume flow rate (volume per unit time) at which air flows through the loop. → Φ depends on the angle θ between v and the plane of the loop. A A rˆN Erwin Sitompul • Unit vector pointing to the normal direction of the plane University Physics: Wave and Electricity 8/5 Flux → If v is perpendicular to the plane (or parallel to the plane’s direction), the rate Φ is equal to vA. → If v is parallel to the plane (or perpendicular to the plane’s direction), no air moves through the loop, so Φ is zero. For an intermediate angle θ, the rate of volume flow through the loop is: (v cos ) A v A This rate of flow through an area is an example of a flux. The flux can be interpreted as the flow of the velocity field through the loop. Erwin Sitompul University Physics: Wave and Electricity 8/6 Flashback: Multiplying Vectors The Scalar Product → → →→ The scalar product of the vector a and b is written as a·b and defined to be: a b ab cos →→ Because of the notation, a·b is also known as the dot product and is spoken as “a dot b.” → → If a is perpendicular to b, means Φ = 90°, then the dot product is equal to zero. → → If a is parallel to b, means Φ = 0, then the dot product is equal to ab. Erwin Sitompul University Physics: Wave and Electricity 8/7 Flashback: Multiplying Vectors The dot product can be regarded as the product of the magnitude of the first vector and the projection magnitude of the second vector on the first vector a b ab cos (a cos )(b) (a)(b cos ) Erwin Sitompul University Physics: Wave and Electricity 8/8 Flashback: Multiplying Vectors When two vectors are in unit vector notation, their dot product can be written as ˆ (b ˆi b ˆj b k) ˆ a b (ax ˆi a y ˆj az k) x y z axbx a y by az bz ˆi ˆj kˆ î 1 0 0 ĵ 0 1 0 k̂ 0 0 1 Erwin Sitompul University Physics: Wave and Electricity 8/9 Flashback: Multiplying Vectors → ^ → ^ ^ ^ What is the angle Φ between a = 3i – 4j and b = –2i + 3k ? z Solution: a b ab cos 3 a 3 (4) 5 2 2 –4 b –2 y a b (2) 2 32 3.606 3 ˆ a b (3iˆ 4ˆj) (2iˆ 3k) ˆ 2i) ˆ (3i)( 6 x ˆi ˆj kˆ î 1 0 0 ĵ 0 1 0 k̂ 0 0 1 6 (5)(3.606) cos 6 1 cos 109.438 (5)(3.606) Erwin Sitompul University Physics: Wave and Electricity 8/10 Flux of an Electric Field The next figure shows an arbitrary Gaussian surface immersed in a nonuniform electric field. The surface is divided into small squares of area ΔA, each being very small to permit us to consider the individual square to be flat. → The electric field E may now be taken as constant over any given square. The flux of the electric field for the given Gaussian surface is: E A • Φ can be positive, negative, or zero, depending → on the → angle θ between E and ΔA Erwin Sitompul University Physics: Wave and Electricity 8/11 Flux of an Electric Field The exact solution of the flux of electric field through a closed surface is: E dA S The flux is a scalar, and its Si unit is Nm2/C. • The electric flux through a Gaussian surface is proportional to the net number of field lines passing through that surface • Without any source of electric field inside the surface as in this case, the total flux through this surface is in fact equal to zero Erwin Sitompul University Physics: Wave and Electricity 8/12 Checkpoint The figure below shows a Gaussian cube of face area A immersed in a uniform electric field E that has the positive direction of the z axis. In terms of E and A, determine the flux flowing through: (a) the front face (xy plane) Φ = +EA Φ = –EA (b) the rear face (c) the top face Φ=0 (d) the whole cube Φ=0 Erwin Sitompul University Physics: Wave and Electricity 8/13 Gaussian Surface: Cylinder The next figure shows a Gaussian surface in the form of a cylinder of radius R immersed in a uniform → electric field E, with the cylinder axis parallel to the field. What is the flux Φ of the electric field through this closed surface? • left cap E dA ( E )(dA)(cos180) a a E dA EA a • right cap E dA ( E )(dA)(cos 0) E dA EA c c c • cylindrical surface E dA E dA E dA E dA S a b EA 0 EA 0 c • zero net flux Erwin Sitompul E dA ( E )(dA)(cos90) b b 0 University Physics: Wave and Electricity 8/14 Gaussian Surface: Cube A electric field given by →nonuniform ^ ^ E = 3xi + 4j N/C pierces the Gaussian cube shown here (x in meters). What is the electric flux through the right face, the left face, and the top face? r E dAr • right face r l 2 (3xˆi 4ˆj) (dydzˆi) 3x dydz 2 2 (3)(3)dydz 36 N m2 C z 0 y 0 Erwin Sitompul (3xˆi 4ˆj) (dydzˆi) x 1 3x dydz z 0 y 0 x 3 2 2 z 0 y 0 2 2 x 3 z 0 y 0 ˆ (dA ˆi) (3xˆi 4j) l 2 z 0 y 0 2 2 • left face l ˆ (dA ˆi) (3xˆi 4j) r r 2 l E dAl x 1 2 (3)(1)dydz 12 N m2 C z 0 y 0 University Physics: Wave and Electricity 8/15 Gaussian Surface: Cube A electric field given by →nonuniform ^ ^ E = 3xi + 4j N/C pierces the Gaussian cube shown here (x in meters). What is the electric flux through the right face, the left face, and the top face? t E dAt • top face t (3xˆi 4ˆj) (dAt ˆj) t 2 3 ˆ (dxdzˆj) (3xˆi 4j) 4 dxdz z 0 x 1 2 3 y 2 z 0 x 1 Erwin Sitompul 16 N m2 C y 2 University Physics: Wave and Electricity 8/16 Example: Flux of an Electric Field In a three-dimensional space, a homogenous electric field of 10 N/C is directed down to the negative z direction. Calculate the flux flowing through: (a) the square ABCD (xy plane) z E (b) the rectangular AEFG (xz plane) 3 (a) E 10kˆ V m AABCD 4kˆ m2 ABCD E AABCD ˆ (4k) ˆ (10k) 40 N m2 C 2 1 F A 2 (b) AAEFG 6jˆ m AEFG E AAEFG ˆ (6ˆj) (10k) 0 Erwin Sitompul G 1 0 B 1 2 3 y 2 3 D C x E University Physics: Wave and Electricity 8/17 Gauss’ Law Gauss’ law relates the net flux Φ of an electric field through a closed surface (a Gaussian surface) to the net charge qenc that is enclosed by that surface. 0 qenc 0 E dA qenc • in vacuum S If you know how much electric field is intercepted by the closed surface, you can calculate how much net charge is inside in the volume of that enclosed surface. Erwin Sitompul University Physics: Wave and Electricity 8/18 Gauss’ Law • S1: Electric field is outward for all points flux is positive enclosed charge is positive • S2: Electric field is inward for all points flux is negative enclosed charge is negative • S3: No charge enclosed • S4: Net charge enclosed is equal to zero, the field lines leaving the surface are as many as the field lines entering it Erwin Sitompul University Physics: Wave and Electricity 8/19 Gauss’ Law: Net Enclosed Charge What is the net charge enclosed by the Gaussian cube of the previous example? b E dAb • bottom face b ˆ (dA ˆj) (3xˆi 4j) b f E dAf • front face b f 2 3 z 0 x 1 2 ˆ 0 (3xˆi 4ˆj) (dAf k) (3xˆi 4ˆj) (dxdzˆj) f y 0 3 4 dxdz z 0 x 1 16 N m2 C y 0 back E dAback • back face back ˆ (dA k) ˆ 0 (3xˆi 4j) back back Erwin Sitompul University Physics: Wave and Electricity 8/20 Gauss’ Law: Net Enclosed Charge What is the net charge enclosed by the Gaussian cube of the previous example? r l t b f back 36 12 16 16 0 0 24 N m2 C qenc 0 E dA S 0 (8.854 1012 )(24) 2.125 1010 C Erwin Sitompul University Physics: Wave and Electricity 8/21 Applying Gauss’ Law: Cylindrical Symmetry The next figure shows a section of an infinitely long cylindrical plastic rod with a uniform positive linear charge density λ, in C/m. We need an expression for the magnitude → of the electric field E at a distance r from the axis of the rod. Due to symmetry, the component of the resultant electric field will be only directed radially outward. EA cos E (2 rh) cos 0 E (2 rh) But, 0 qenc 0 E (2 rh) h Erwin Sitompul • What about top cap and bottom cap E 2 0 r University Physics: Wave and Electricity 8/22 Applying Gauss’ Law: Planar Symmetry Imagine a thin, infinite sheet with a uniform (positive) surface charge density σ, in → C/m2. Now, let us find the electric field E a distance r in front of the sheet. A useful Gaussian surface in this case is a closed cylinder with end caps of area A, arranged to pierce the sheet perpendicularly, as shown. 0 E dA qenc S 0 ( EA EA) A • What is the direction of the electric field? Erwin Sitompul E 2 0 University Physics: Wave and Electricity 8/23 Example: Single Thin Plate Charge of 10–6 C is given to a 2-m2 thin plate. Afterwards, an electron with the mass 9.109×10–31 kg with the charge 1.602×10–19 C is held in a distance 10 cm from the plate. (a) Determine the force acting on the electron. (b) If the electron is released, determine the speed of the electron when it hits the plate. q 106 5 107 C m2 (a) A 2 5 107 4 E 2.824 10 NC 12 2 0 2(8.854 10 ) away from the plate 15 F qE (1.602 1019 )(2.824 104 ) 4.524 10 N toward the plate Erwin Sitompul University Physics: Wave and Electricity 8/24 Example: Single Thin Plate Charge of 10–6 C is given to a 2-m2 thin plate. Afterwards, an electron with the mass 9.109×10–31 kg with the charge 1.602×10–19 C is held in a distance 10 cm from the plate. (a) Determine the force acting on the electron. (b) If the electron is released, determine the speed of the electron when it hits the plate. F 4.524 1015 15 2 4.967 10 m s (b) a m 9.109 1031 v 2 v02 2a( x x0 ) (0) 2 2(4.967 1015 )(0 0.1) 9.934 1014 v 3.152 107 m s toward the plate Erwin Sitompul University Physics: Wave and Electricity 8/25 Example: Double Parallel Plates Two large, parallel plates, each with a fixed uniform charge on one side, is shown below. The magnitudes of the surface charge densities are 2 2 σ(+) = 6.8 μC/m → and σ(–) = 4.3 μC/m . Find the electric field E (a) to the left (L) of the plates (b) between (B) the plates (c) to the right (R) of the plates E( ) () 6.8 106 5 3.840 10 NC 12 2 0 (2)(8.854 10 ) away from the (+) plate E( ) ( ) 4.3 106 5 2.428 10 NC 12 2 0 (2)(8.854 10 ) toward the (–) plate Erwin Sitompul University Physics: Wave and Electricity 8/26 Example: Double Parallel Plates (a) EL E( ) E( ) 3.840 105 2.428 105 1.412 105 N C away from the (+) plate (b) EB E( ) E( ) 3.840 105 2.428 105 6.268 105 N C away from the (+) plate (c) ER E( ) E( ) 3.840 105 2.428 105 1.412 105 N C away from the (–) plate Erwin Sitompul University Physics: Wave and Electricity 8/27 Applying Gauss’ Law: Spherical Symmetry A spherical shell of uniform charge attracts or repels a charged particle that is outside the shell as if all the shell’s charge were concentrated at the center of the shell. 1 q E , 2 4 0 r rR If a charged particle is located inside a spherical shell of uniform charge, there is no electrostatic force on the particle from the shell. E 0, Erwin Sitompul rR University Physics: Wave and Electricity 8/28 Applying Gauss’ Law: Spherical Symmetry Any spherically symmetric charge distribution, such as on the figure, can be constructed with a nest of concentric spherical shells. If the entire charge lies within a Gaussian surface, r > R, the charge produces an electric field on the Gaussian surface as if the charge were a point charge located at the center. If only a portion of the charge lies within a Gaussian surface, r < R, then the charge enclosed q’ is proportional to q. E q 4 0 R Erwin Sitompul 3 r, rR University Physics: Wave and Electricity 8/29 Checkpoint The figure shows two large, parallel sheets with identical (positive) uniform surface charge densities, and a sphere with a uniform (positive) volume charge density. Rank the four numbered points according to the magnitude of the net electric field there, greatest first. 3 and 4 tie, then 2, 1. • The electric field contributed by the two parallel sheets is identical at all numbered points. • The closer to the sphere, the greater the electric field contributed by it. Erwin Sitompul University Physics: Wave and Electricity 8/30 Email Quiz A long thin cord has a positive a linear charge density of 3.1 nC/m. The wire is to be enclosed by a coaxial, thin cylindrical shell of radius 1.8 cm. The shell is to have negative charge on its surface with a surface charge density that makes the net external electric field zero. Calculate the surface charge density σ of the cylindrical shell. E 0 Erwin Sitompul University Physics: Wave and Electricity 8/31 Homework 7 (a) The rectangle ABCD is defined by its corner points of A(2,0,0), B(0,3,0), C(0,3,2.5), and D(2,0,2.5). Draw a sketch of the rectangular. → ^ ^ (b) Given an electric field of E = –2i + 6j N/C, draw the electric field on the sketch from part (a). (c) Determine the number of flux crossing the area of the rectangular ABCD. Erwin Sitompul University Physics: Wave and Electricity 8/32 Homework 7A 1. (a) The triangle FGH is defined by its corner points of F(2,0,0), G(0,3,0), and H(0,0,4). Draw a sketch of the triangle. → ^ ^ (b) Given an electric field of E = –2i + 6j N/C, draw the electric field on the sketch from part (a). (c) Determine the number of flux crossing the area of the triangle FGH. → ^ ^ 2. A rectangle is under the influence of electric field of E = 2xyi + 4zk N/C. The dimension of the rectangle is 1 m × 2 m × 3 m, with x1 = 5 m and y1 = 4 m. What is the electric flux flowing through the front face and top face? Erwin Sitompul University Physics: Wave and Electricity 8/33