Download bio98a_l09

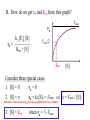
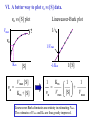
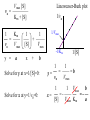
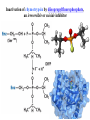
Bio 98 - Lecture 9
Enzymes II: Enzyme Kinetics
Amino acid side chains with titratable groups
Appr. pKa
Carboxylate
4
Amine/guanidi
nium
10-12
Sulfhydryl
8
Imidazole
6
Hydroxyl
13 (lecture 8!)
Hydroxyl
10
Enzyme catalyzed reaction
G (free energy)
S
E
P
S‡
ES‡
G‡
E+S
E+P
G
Reaction coordinate
1. Enzymes do not alter the equilibrium or G.
2. They accelerate reactions by decreasing G‡.
3. They accomplish this by stabilizing the transition state.
I. Enzyme reactions have at least two steps
E+S
k1
k-1
binding step
- rapid
- reversible
ES
k2
E+P
catalytic step
- slower
- irreversible (often)
ES = “enzyme-substrate complex”
≠ transition state (ES‡)
(1) What is the physical meaning of the constants? What do they
tell us about effectiveness of binding & catalysis?
(2) How can we determine experimentally the value of these
constants for a given enzyme?
II. Enzyme kinetics: Michaelis-Menten equation
E+S
k1
ES
k2
E+P
k-1
d[P]
k2 [E]t [S]
Initial reaction rate = ––– = vo = –––––––––
dt
Km + [S]
Michaelis-Menten
equation
[E]t = concentration of total enzyme
[S] = concentration of free substrate
Information obtained from the
study of vo vs [S]
k2: catalytic power of the enzyme
(turnover rate), aka kcat; unit: 1/s
Km: effectiveness (affinity) with
which enzyme E binds S; unit: M
Rate of breakdown of ES
k-1 + k2
Km = ––––––
k1
Rate of formation of ES
III. How do we measure k2 and Km values?
A. Typical experiment
urease (0.1 M)
(urea)
+ H2O
CO2 + 2 NH3
Raw data
urea
(mM)
5
10
20
50
etc
velocity/rate
(M CO2/min)
30
50
80
100
Vmax
100
vo
50
[urea]
III. Why is there a Vmax?
urease (0.1 M)
(urea)
+ H2O
CO2 + 2 NH3
Vmax
100
vo
50
[urea]
B. How do we get k2 and Km from this graph?
Vmax
vo
k2 [E]t [S]
vo = –––––––––
Km + [S]
Vmax/2
Km
[S]
Consider three special cases
1. [S] = 0
vo = 0
2. [S] ≈ ∞
vo ≈ k2 [E]t = Vmax, so k2 = Vmax / [E]t
Remember a finite number (Km) becomes negligible in the face of infinity
3. [S] = Km
when vo = ½ Vmax
Assumptions for steady-state kinetics
E+S
k1
k-1
ES
k2
E+P
The Michaelis-Menten equation assumes
that the chemical reaction has reached
steady state:
• [ES] remains constant over time
• presteady state (the build up of the ES
complex) happens in microseconds
• Usually nM [enzyme] but mM
[substrate] in reaction, so [S] >> [E]
k2 [E]t [S]
vo = –––––––––
Km + [S]
Vmax [S]
with k2 [E]t = Vmax, then vo = –––––––––
Case 2 from previous slide!
Km + [S]
IV. What is the physical meaning of k2?
Suppose [E]t = 0.01 µM,
Vmax = 200 µM/min
Vmax
200 µM/min
k2 = –––––– = –––––––––––– = 20,000 min-1
[E]t
0.01 µM
so 20,000 moles of P produced per min per mole of E
k2 is the # of reactions a single enzyme
molecule can catalyze per unit time
k2 = kcat = “catalytic constant” or “turnover
number”, expressed in catalysis events per time.
V. What is the physical meaning of Km?
E+S
k1
k-1
ES
k2
E+P
Rate of breakdown of ES
k-1 + k2
k-1
Km = –––––– ≈ ––– = Kdiss
k1
k1
Rate of formation of ES
provided (k2 << k-1)
Remember: k2 is rate-limiting thus
rate is slower than k-1 and thus k2
numerically much smaller than k-1
1. Km is a measure of how tightly an enzyme binds its substrate.
2. It is the value of [S] at which half of the enzyme
molecules have their active sites occupied with S, generating ES.
3. For a given enzyme each substrate has its own Km.
4. Lower Km values mean more effective binding.
Consider Km = 10-3 vs. 10-6 M (high affinity vs low affinity, compare to P s for T
50
and R states of hemoglobin, lecture 7)
VI. A better way to plot vo vs [S] data.
vo vs [S] plot
Vmax
Lineweaver-Burk plot
?
vo
1/vo
1/Vmax
Km
[S]
Vmax [S]
vo = –––––––––
Km + [S]
-1/Km
1/[S]
1
Km
1
1
–– = –––– ––– + –––––
vo
Vmax [S]
Vmax
Lineweaver-Burk eliminates uncertainty in estimating Vmax.
The estimates of Vmax and Km are thus greatly improved.
Vmax [S]
vo = –––––––––
Km + [S]
Take reciprocal of both sides of equation
Km + [S]
1
= ––––––––
vo
Vmax [S]
Expand
Thus
[S]
K
1
m
+
= ––––––––
vo Vmax [S]
Vmax[S]
1
Km
1
1
–– = –––– ––– + –––––
vo
Vmax [S]
Vmax
Lineweaver-Burk
y = ax + b
Lineweaver-Burk plot
Vmax [S]
vo = –––––––––
Km + [S]
1/vo
1
Km
1
1
–– = –––– ––– + –––––
vo
Vmax [S]
Vmax
y =
a
x
+
1/Vmax
-1/Km
1/[S]
b
Solve for y at x=1/[S]=0:
1
1
y = –– = –––– = b
vo
Vmax
Solve for x at y=1/v0=0:
1
1 Vmax
b
x = –– = - –––– –– = - ––
[S]
Vmax Km
a
VII. Enzyme efficiency
Efficiency = kcat / Km (specificity constant)
Combines an enzyme’s catalytic potential with its
ability to bind substrate at low concentration.
Example – which enzyme is more efficient?
Enzyme
Km
Chymotrypsin
kcat
kcat/Km
0.015 M
0.14 s-1
9.3
0.0003 M
0.50 s-1
1,700
Ac-Phe-Gly Ac-Phe + Gly
Pepsin
Phe-Gly
Phe +Gly
VIII. Enzyme inhibition - what to know
1. Reversible vs. irreversible inhibition
• What is the difference?
2. Competitive inhibition
• Know how to recognize or draw the model.
• Know how vo vs [S], and Lineweaver-Burk plots
are affected by competitive inhibition.
• What are  and Ki?
3. Irreversible inhibition
• What is it; how does it work; what is its use?
• What are suicide inhibitors, how do they work?
• Know one example.
Classical competitive inhibition
where I is the inhibitor
K1
How do you measure competitive inhibition?
K1
-1/Km
Vmax [S]
vo = –––––––––
Km + [S]
where
[I]
 = 1 + –––
KI
[E][I]
KI = ––––––
[EI]
Vmax remains unchanged, but apparent Km increases with increasing [I]
Inactivation of chymotrypsin by diisopropylfluorophosphate,
an irreversible or suicide inhibitor
Chymotrypsin is a serine protease that
cleaves a peptide at Phe/Tyr/Trp (C) leaving a COO- on Phe/Tyr/Trp
Inhibitor (diisopropylfluorophosphate)
R2
Aspirin acts as an acetylating agent where an acetyl group
is covalently attached to a serine residue in the active site
of the cyclooxygenase enzyme, rendering it inactive.