Download Through Confidence Limits

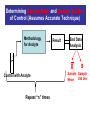
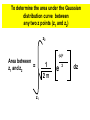
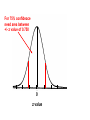
Quality Control
Procedures put into place to monitor
the performance of a laboratory test
with regard to accuracy and precision
Question
What is the difference between accuracy
and precision?
Accuracy – measure of how close
experimental value is to true value
Precision –measure of reproducibility
Ways to estimate true value
1. Mean (average) (X)
X = Σxi/n
xi - single measured value
n- number of measured values
2. Median – Order xi values, take middle value
(if even number of xi values - take average values of two middle values)
3. Mode – most frequent xi value
If above is to estimate the true value what does this assume?
Proposed way to measure precision
Average Deviation
=
Σ(X – xi)/n
Does this estimate precision?
No – because the summation equals zero, since xi
values are less than and greater than the mean
Ways to Measure Precision
1.Range (highest and lowest values)
2. Standard Deviation
Standard Deviation
s=
Σ(xi – X)2
(n-1)
s – standard deviation
xi - single measured value
X – mean of xi values
n - number of measured values
Variations of Std Dev
1. Variance -
std. dev. squared (s2)
Variances add, NOT std deviations.
To determine total error for a measurement that
has individual component standard deviations for
the measurement s1, s2, s3, etc [i.e., random error
in diluting calibrator (s1), temperature change (s2),
noise in spectrophotometer (s3), etc.]
(stotal)2 = (s1)2 + (s2)2 + (s3)2 + …
Variations of Std Dev (cont.)
2. Percent Coefficient of Variation (%CV)
%CV = 100 * S/X
Monitoring Performance with
Controls
1. Values of controls are measured multiple
times for a particular analyte to determine:
a) “True value” – usually X
b) Acceptable limits - usually +
- 2s
2. Controls are run with samples and if the
value for the control is within the range
X +
- 2s then run is deemed acceptable
Determining Sample Mean and Sample Std Dev
of Control (Assumes Accurate Technique)
Methodology
for Analyte
Result
End Data
Analysis
X
Control with Analyte
Repeat “n” times
s
Sample Sample
Std Dev
Mean
Determining True Mean and True Std Dev of
Control (Assumes Accurate Technique)
Methodology
for Analyte
Result
End Data
Analysis
μ
True
Mean
Control with Analyte
Repeat
∞
times
σ
True
Std Dev
There is another way!!!
Statistics
Sample
Population
μ σ
(of population)
Take finite
sample
Statistics
X s
Gives range around
X and s that μ and σ
will be with a given
probability
Rather than measuring every
single member of the population,
statistics utilizes a sampling of the
population and employs a
probability distribution description
of the population to “estimate
within a range of values” µ and σ
Probability Distribution
Number or frequency
of the value
Continuous function of frequency (or
number) of a particular value versus the
value
Value
Properties of any
Probability Distribution
1. Total area = 1
Number or frequency
of the value
2. The probability of value x being between a and b is the
area under the curve from a to b
a
b
Value
The most utilized probability
distribution in statistics is?
Gaussian distribution
Also known as Normal distribution
Parametric Statistics – assumes
population follows Gaussian distribution
Gaussian Distribution
1. Symmetric bell-shaped curve centered on μ
Number or frequency
of the value
2. Area = 1
3. 68.3% area μ + 1σ (area = 0.683)
95.5% area μ + 2σ (area = 0.955)
99.7% area μ + 3σ (area = 0.997)
µ
µ
µ
-
-
-
3σ 2σ
1σ
μ
µ
µ
µ
+
+
+
1σ 2σ 3σ
x (value)
What Gaussian Statistics First Tells Us
Area under the curve gives us the probability that individual
value from the population will be in a certain range
1) 68.3% chance between μ + 1σ and μ - 1σ
2) 95.5% chance between μ + 2σ and μ - 2σ
3) 99.7% chance between μ + 3σ and μ - 3σ
Number or frequency
of the value
These are the chances that a random point
(individual value) will be drawn from the
population in a given range for Gaussian
population
0.683
0.955
0.997
µ
µ
µ
-
-
-
3σ 2σ
1σ
μ
µ
µ
µ
+
+
+
1σ 2σ 3σ
x (value)
Gaussian Distribution Equation
f(x) =
1
2 πσ2
e
Number or frequency
of the value [f(x)]
-(x - µ)2
2σ2
µ
µ
µ
-
-
-
3σ 2σ
1σ
µ
µ
µ
µ
+
+
+
1σ
2σ 3σ
x (value)
Gaussian curves are a family of distribution
curves that have different µ and σ values
-(x - µ)2
f(x) =
1
2 πσ2
e
A. Changing µ
2σ2
B. Changing σ
To determine area between any two x values
(x1 and x2) in a Gaussian Distribution
x2
1
Area
f(x)
=
between =
x1 and x2
2 πσ2
e
Number or frequency
of the value [f(x)]
-(x - µ)2
dx
2σ2
x1
µ
µ
-
-
x1
3σ 2σ
µ
1σ
x2
µ
µ
µ
µ
+
+
+
1σ
2σ 3σ
x (value)
Any Gaussian distribution can be
transposed from x values to z values
x value equation
x2
-(x - µ)2
1
Area =
2 πσ2
e
2σ2
dx
z = (x - µ)/σ
x1
z value equation
z2
-(z)2
1
Area =
z1
2π
e
2
dz
To determine the area under the Gaussian
distribution curve between
any two z points (z1 and z2)
z2
-(z)2
Area between
=
z1 and z2
1
2π
z1
e
2
dz
Transposition of x to z
z = (x - µ)/σ
The z value is the x value written
(transposed) as the number of
standard deviations from the mean.
It is the value in relative terms with
respect to µ and σ. z values are for
Gaussian distributions only.
At this point, we can use Gaussian statistics to
determine the probability of selecting a range of
individuals from a population (or that an analysis will
give a certain range of values).
What is the probability that a healthy individual will have a serum
Na concentration between 141 and 143 mEq/L (σ = 2.5 mEq/L)?
Normal range of [Na] in serum
143
-(x - 140)2
Area =
1
2 π(2.5)2
e
2(2.5)2
dx
141
You could theoretically do it this
way, however the way it is done is
to transpose and use table
135
140
[Na] mEq/L
(x)
145
To do this need to transpose x to z va and use the table
What is the probability that a healthy individual will have a serum
Na concentration between 141 and 143 mEq/L (σ = 2.5 mEq/L)?
Transpose x values to z values by:
Normal range of [Na] in serum
z = (x – μ)/σ
Which for this problem is:
z = (x – 140)/2.5
Thus for the two x values:
z = (141 – 140)/2.5 = 0.4
-2
z = (143 – 140)/2.5 = 1.2
-1 0
z
1
2
0.4
135
140
x
1.2
145
To do this, need to transpose x to z values and use the table
What is the probability that a healthy individual will have a serum
Na concentration between 141 and 143 mEq/L?
So to solve for area:
Normal range of [Na] in serum
1. Determine area between z=0 to z = 1.2
Area = 0.3849 (from table)
2. Determine area between z=0 to z=0.4
Area = 0.1554 (from table)
3. Area from z=0.4 to z=1.2
0.3849 – 0.1554 = 0.2295
-2
-1 0
z
1
2
0.4
Answer: 0.2295 probability
135
140
x
1.2
145
Our goal: To determine μ
Cannot determine μ
What can we determine about μ ?
The Problem
Establishing a value of μ of the population
The Statistics Solution
1. Take a sample of X from the population.
2. Then from statistics, one can make a
statement about the confidence that
one can say that μ is within a certain
range around X
Sample
Population
μ σ
(of population)
Take finite
sample
Statistics
X s
Gives range around
X and s that μ and σ
will be with a given
probability
Distribution of Sample Means
How Statistics Gets Us Closer to μ
Distribution of Sample Means
– Example of [Glucose]serum in Diabetics
Population
of Diabetics
Sample means
are determined
X1
μ
X2
X3
XN
For this example:
n=25
N=50
n - sample size (# of
individuals in
sample)
N – number of trials
determining mean
By theory, the
distribution of sample
means will follow the
Central Limit Theorem
Central Limit Theorem
Sample means (X) of taken from a population are
Gaussian distributed with:
1)mean = μ
2)std dev =σ/ n
(μ true mean of the population)
(σ is true std dev for the population, n
is sample size used to determine X)
[called standard error of the mean (SEM)]
Conditions:
1) Applies for any population that is Gaussian [independent of sample
size (n)]
2) Applies for any distributed population if the sample size (n) > 30
3) Assumes replacement or infinite population
Central Limit Theorem
Number or frequency
of X
μ is true mean of
the population
σ is true std dev for
the population
n is sample size
used to
determine X)
μ
μ
-
-
2σ/ n 1σ/ n
μ
μ
-
-
2 SEM 1 SEM
μ
μ
μ
+
+
1σ/ n 2σ/ n
μ
μ
+
+
1 SEM 2 SEM
X (Sample Means)
The absolute width of the distribution of sample means is
dependent on “n”, the more points used to determine X the
smaller
?
__________
the width.
SEM =σ/ n
μ
μ
-
-
2 SEM 1 SEM
μ
μ
μ
+
+
1 SEM 2 SEM
X (Sample Means)
Larger sample size “n”
SEM =σ/ n
Smaller sample size “n”
X (Sample Means)
-(X - µ)2
1
f(X) =
e
2SEM2
2 π SEM2
SEM =σ/ n
Transposing:
z = (X - µ)/SEM
μ
μ
-
-
μ
2SEM 1SEM
μ
μ
+
+
1SEM 2SEM
-(z)2
X (Sample Means)
-3
-2
-1
0
z value
1
2
3
f(z) =
1
2π
e
2
What does a z value mean?
The number of standard deviations from the mean.
z values are for Gaussian distributions only.
For the population distribution of x values, z=
Std dev = σ and mean = μ So z =
z = (x - µ)/σ
For the sample mean distribution of X values, z=
Std dev = SEM and mean = μ So z =
z = (X – μ)/SEM
How the distribution of sample
means is used to establish the
range in which the true mean μ can
be found (with a given probability or
confidence)
1) An experiment is done in which ONE sample
mean is determined for the population
2) Because the distribution of sample means follows
a Gaussian distribution then a range with a
certain confidence can be written
There is a 95.5% chance
(confidence) that the one
determination of X will be in
the range indicated.
This range can be
written mathematically
as:
Area = 0.955
μ
μ
-
-
2 SEM 1 SEM
μ
μ
μ
+
+
μ – 2SEM < X < μ + 2SEM
1 SEM 2 SEM
X (Sample Means)
However this does not
answer our real question,
we want the range that μ is
in!
We have are the 95.5% confidence limits for X
What we want are the 95.5% confidence limits for μ
We get this by simply rearranging the expression
μ – 2SEM < X < μ + 2SEM
Subtract μ from each part of the expression
– 2SEM < X - μ < + 2SEM
Subtract X from each part of the expression
-X– 2SEM < - μ < - X + 2SEM
Multiply each part of the expression by -1
+X +2SEM > +μ > +X - 2SEM
Writing so range is given as normal (going from lower to upper limit)
X - 2SEM < μ < X + 2SEM
X - 2SEM < μ < X + 2SEM
This 95% confidence range for μ can be written as
the following + expresion:
X + 2SEM
A range for μ can be written for any
desired confidence
99.7 % confidence?
X + ? SEM
68.3 % confidence?
X + ? SEM
75.0% confidence?
X + ? SEM
What z value do you put in?
For 75% confidence
need area between
+/- z value of 0.750
0
z value
General Expression for Range μ is
Within with Specified Confidence
Estimator of μ + (Confidence Coefficient) x (SD of Estimator
Distribution)
z value
X
[chose z value whose area between
the +Z and –z value equals the
probability (confidence) desired ]
SEM
(σ/ n)
σ – population true std dev
n – size of sample used to determine X
Problem
What range would µ be within from a
measured X of 159 mg/dL (sample size
=25) if σ = 10 mg/dL with a 76%
confidence? With a 95% confidence?