Download Human Genetic Revolution

Linkage analysis: Two-factor testcross
AaBb x aabb
AaBb, Aabb, aaBb, aabb
What are the implications of phenotypes
scored on these progeny?
Linkage analysis: Two-factor testcross
• Double heterozgyotes are mated with homozygous
recessives
• Genotypes of a large number of progeny are
scored
• If locus A and B are on different chromsomes,
alleles will follow Mendel’s law of Independent
Assortment
• Genetically linked? Two of four genotypes more
frequent than expected (c2 test statistic)
Linkage analysis: Interval mapping (Haley
and Knott, 1992)
A
Q
rA
B
rB
rAB = rA + rB - 2rArB
Frequencies for F1 gametes and RI
genotypes (Markel et al., 1996)
F1 gametes
Frequency
RI genotype
Frequency
A1B1
(1 - R')/2
A1A1B1B1
(1 - R)/2
A1B2
R'/2
A1B1B2B2
R/2
A2B1
R'/2
A2A2B1B1
R/2
A2B2
(1 - R')/2
A2A2B2B2
(1 - R)/2
RI genotypic frequencies of two flanking
markers and an intermediate QTL (Markel et
al., 1996)
Genotype
Predicted Frequency
A1A1Q1Q1B1B1
A1A1Q2Q2B1B1
A1A1Q1Q1B2B2
A1A1Q2Q2B2B2
A2A2Q1Q1B1B1
A2A2Q2Q2B1B1
A2A2Q1Q1B2B2
A2A2Q2A2B2B2
(1 - RA)(1 - RB)/2
RARB/2
(1 - RA)RB/2
RA(1 - RB)/2
RA(1 - RB)/2
(1 - RA)RB/2
RARB/2
(1 - RA)(1 - RB)/2
Expected additive effect coefficients of each
pair of RI genotypes (Markel et al., 1996)
RI Genotypes
Expected additive effect
A1A1B1B1
[(1 - RA - RB)/(1 - R)](a)
A1A1B2B2
[(RB - RA)/R](a)
A2A2B1B1
[(RA - RB)/R](a)
A2A2B2B2
[(RA + RB - 1)/(1 - R)](a)
Coefficients (xi) of the additive effect of a QTL at five
positions between two flanking markers of A and B
that are 20 cM apart (Markel et al., 1996)
Position of QTL (cM)
Genotype
0
5
10
15
20
A1A1B1B1
1.00
0.84
0.79
0.84
1.00
A1A1B2B2
1.00
0.43
0.00
-0.43
-1.00
A2A2B1B1
-1.00
-0.43
0.00
0.43
1.00
A2A2B2B2
1.00
-0.84
-0.79
-0.84
-1.00
Maximum likelihood approach to QTL
mapping (Lander and Botstein, 1988)
• Assuming complete map coverage, is it
possible to design a cross to make it highly
likely that QTLs will be found?
• Using flanking markers as opposed to
single-marker analysis
• Reduce the number of markers individually
tested and thus reduce type I error
Traditional approach
• Compare the mean phenotypic value of
progeny with genotype AB to those with
marker genotype AA
• One-way analysis of variance
– i.e., a linear regression
– assume normally-distributed residual
environmental variance
Number of progeny required for detection
(Soller and Brody, 1976)
• Assume that a QTL contributes s2exp to the genetic
variance and is located exactly at a marker locus
• (Za)2(s2res/s2exp)
– Za is the number of standard deviations beyond with
the normal curve contains probabilty a
• Phenotypic effect may be underestimated if not at marker
locus
• Greater number of progeny if not at the marker
• No definition of the likely position of the QTL
• Multiple testing
Interval mapping of QTLs using LOD scores:
Method of maximum likelihood

fi=a + bgi + e
· gi is coded (0, 1) for number of B alleles
 e is a random normal variable with mean 0 and
variance s2
· b denotes the estimated phenotypic effect of a
single allele substitution at a putative QTL
• L(a, b, s2) = Piz((fi - (a + bgi)), s2)
• LOD = log10(L(a’, b’, s2’)/L(mA’, ), s2B’))
Interval mapping of QTLs using LOD scores:
Method of maximum likelihood
• ELOD = 1/2log10(1 + s2exp/s2res) (a result
from linear regression)
• ~1/2(log10e)(s2exp/s2res) (Taylor expansion
for small values of s2exp/s2res)
• ~0.22(s2exp/s2res)
• T/ELOD ~ (Za)2/(s2exp/s2res)
Interval mapping of QTLs using LOD
scores(Lander and Botstein, 1988)
• L(a, b, s2) = Pi[Gi(0)Li(0) + Gi(1)Li(1)]
• Li(x) = z((fi - (a + bx)), s2) denotes
likelihood function for individual I
• Assumptions
– gi = x
– Gi(x) denotes the probability that gi = x
conditional on the genotypes and positions of
the flanking markers
Confirmation of EtOH sensitivity QTL in mouse
(Markel et al., 1997)
Genetic map of EtOH-sensitivity QTL (Lore1 - 6;
Markel et al., 1997)
Additive effect of confirmed QTL for
alcohol sensitivity (Markel et al., 1997)
Marker-assisted breeding of congenic mouse
strains (Markel et al, 1997b)
• Yellow indicates the
donor (D) genome
• Blue represents the
recipient (R) genome
• Apoe is the target
region of introgression
• Left side represents
traditional approach,
while right the “speed”
congenic method
Traditional congenic breeding strategy
(Markel et al., 1997b)
Generation
F1
N2
N3
N4
N5
N6
N7
N8
N9
N10
Average %
% recipient genome
heterozygous (D/R)
segments  SD
100.00
50.00
75.00
50.007.07
87.50
25.005.00
93.75
12.503.54
96.88
6.252.50
98.44
3.131.76
99.22
1.561.25
99.61
0.780.88
99.81
0.390.63
99.90
0.200.44
Marker-assisted congenic breeding strategy
(Markel et al., 1997)
Backcross
generation
Average %
D/R segments
SD
% D/R
segments in
'best' male
% recipient
genome of
'best' male
F1
1000
100
50
N2
N3
50.007.07
19.164.38
38.32
11.93
80.84
94.03
N4
N5
5.982.44
0.980.98
1.95
~0
99.03
~100
Theoretical potential (Markel et al.,
1997b)
Number of male carriers
5
10
15
20
30
40
50
Potential reduction in
D/R (sx)
0.85
1.29
1.50
1.65
1.84
1.96
2.06
Comparison of theoretical expectations and
empirical data
Recipient
Strain at N5
BABL/cByJ
C3H/HeJ
C57BL/Ks
CAST/Ei
DBA/2J
FVB/NJ
Estimated %
recipient
genome for
best male
99.52
99.27
99.66
92.74 (N4)
98.97
99.38
Observed %
recipient
genome for
best male
99.11
99.41
99.70
95.54 (N4)
99.38
99.73
Lecture 4: Mapping in humans (1 of 2)
• Linkage analysis
• Relative-pair analysis
Genetic mapping has been uncommon
for human in most of the last century
• Lack of abundant supply of markers
• Inability to arrange human crosses to suit
experimental purposes
• Breakthrough with Botstein et al. (1980) for yeast
• Use naturally occurring DNA sequence variation
in humans
• Led to mapping several hundred rare Mendelian
diseases
Human Genetic Revolution
• Human genetics has sparked a revolution in
medical science
• Can find genes behind disease without
knowing how they function
• Completely generic approach
Last two decades ushered in complex traits
• Do not follow simple Mendelian monogenic
inheritance
• Heart disease, hypertension, diabetes,
cancer, and infection
Defining disease
•
•
•
•
Clinical phenotype
Age at onset
Family history
Severity
The Population
Allele frequencies
+
Environment
The Metric
The Sample
Method/
Technique
+
Time/
Place
}
• Prevalence
• Risk
• Heritability
• Age of onset
• Family history
• Severity etc.
Linkage Analysis: Overview
• Simple Mendelian traits offer a small
number of hypotheses for the geneticist to
test.
• Thus, the geneticist speculates based on
Mendelian rules what the most appropriate
model is to explain the pattern of
relationship between observed phenotype
and genotype.
Linkage analysis: Hypothesis
• For simple mendelian traits, mendelian rules of gametic
transmission can explain adequately the pattern of
phenotypes in a multigenerational family:
• M1 = a specified model that suggests a specific location for
a trait-causing gene
• Much more likely to have produced the observed data than
• M0 = a model that suggests no linkage to a trait-causing
gene in the region
Linkage analysis: Hypothesis
• The evidence for M1 versus M0 is measured by the
likelihood ratio
LR = Prob(Data|M1)/Prob (Data|M0)
• This is also presented as Z, the lod score
Z = log10(LR)
• (see 49, 50; Morton (1955))
Autosomal dominant trait
1
t/t
M1/M2
1
2
T / t, M1 / M2
t / t, M2 / M2
2
3
T/t
T/t
M2/M2 M2/M2
4
5
T/t
T/t
M1/M2 M1/M2
6
t/t
M1/m2
Basic calculations in human linkage analysis
• Assign linkage phase
• Calculate conditional probabilities
• Observe the number of each class of paternal
gametes in progeny
• Probability of observed family given a model
[L(q)]
• Probability assuming independent assortment
[L(0.5)]
• Calculate likelihood ratio: LR = L(q)/L(0.5)
Assign linkage phase
• Equivalent to experimental two-factor testcross
• Linkage phase
– Different sets of alleles on each member within
a pair of homologous chromosomes (i.e,
haplotype)
– AB/ab is in coupling; Ab/aB is in repulsion
– Marker alleles are codominant, so phase is
arbitrary; coupling is TM1/tM2 and repulsion is
tM1/TM2
Conditional probabilities
Gamete Frequencies
Phase
TM1
TM2
tM1
tM2
Coupling
(1 - q)/2
q/2
q/2
(1 - q)/2
Repulsion
q/2
(1-q)/2
(1-q)/2
q2
n1
n2
n3
n4
Observe paternal gametes
• n1 = TM1, n2 = TM2, n3 = tM1, and n4 =
tM2 gametes
• Six children in the present example
–
–
–
–
n1 = 1
n2 = 2
n3 = 3
n4 = 0
Probability L(q)
• Each offspring is an independent event so that:
• L(q) = L(coupling)L(q) + L(repulsion)L(q)
=0.5[0.5n(1 - q)n1+n4(q)n2+n3]+0.5[0.5n(1 q)n2+n3(q)n1+n4]
=0.5n+1[(1- q)n1+n4(q)n2+n3+(1- q)n2+n3(q)n1+n4]
• The geneticist provides a reasonable value for q;
in this case, what is a reasonable value for q?
Probability L(.167)
• L(0.167)
= (0.5)7[(0.833)1(0.167)5+(0.833)5(0.167)1]
= 0.000524
L(0.5)
• L(0.5)=.25n, n is the number of progeny
• L(0.5)
=(0.25)6
=0.000244
LR and Z
• LR = L(q)/L(0.5)
= 0.00052/0.00024
= 2.147
• Z = log10LR = 0.332
• Try different values of q
• If recombinants (r) can be counted directly, then
maximum likelihood estimate (MLE) = r/n
t/t, M1/M2
T/t, M2/M2
1
1
t/t
M1/M2
2
1
2
T / t, M1 / M2
t / t, M2 / M2
2
3
T/t
T/t
M2/M2 M2/M2
4
5
T/t
T/t
M1/M2 M1/M2
6
t/t
M1/m2
Father’s genotype is in repulsion
• Assume father’s alleles are in repulsion (TM2/tM1)
– L(q)=0.5n(1 - q)n2+n3(q)n1+n4
– L(0.167)=(0.5)6(0.833)5(0.167)=0.001046
• Multiple generations are thus valuable
– Nearly twice the earlier value
– Z improves by 0.3, underscoring the value of multigeneration pedigrees
• How about two families of 6 children versus one family of
12?
Linkage analysis: Autosomal recessive trait
• More complicated analysis; more families are required to
demonstrate linkage between a marker locus and an
autosomal recessive trait compared to autosomal dominant
• Normal children can be Tt or TT; thus, alone can not be
used to deduce linkage phase of doubly-heterozygous
parent
• Families with just one affected are not informative, even
when several normal children are available
• LR(q)=0.5[(1-q)1(q)0+(q)1(1-q)0]
=0.5[(1-q)+q]
=0.5
Allele frequency estimation
• Allelic heterogeneity
• Critical; rare versus common allele
Allele-sharing studies
•
•
•
•
•
Penrose (1935)
Haseman and Elston (1972)
Carey and Williamson (1993)
Fulker and Cardon (1994)
Lander et al. (1995)
Allele-sharing: Haseman and Elston (1972)
• Can genetic variance be assigned to a locus?
• Twin studies
– Partition genetic variance
– Do not address the contribution of individual
loci
• Sib-pairs
– Addresses secular and age effects
– Include information about parents
Allele-sharing: Haseman and Elston (1972)
• Xij = m + gij + eij
• gij = genotypic value; eij = environmental
deviation
• Assume random mating and linkage equilibrium
• Yj = (sib-pair difference)2
• Estimate Y based on best estimate of the number
of alleles the sibs share identical by descent (IBD)
Allele-sharing: Haseman and Elston (1972)
• Let pj = proportion of genes shared IBD and
Y = (x1j - x2j)2 for sib pair j
• Develop expectation of Y if p known
precisely at the disease locus
• Estimate p (p’) given the genotypes of the
parents (sometimes) and children for marker
locus
• Predict Y based on p’
Development of the model
• E (Yj | pj)
• E (p’ | Im)
 p’ = estimate of p
– Im = information about parent and sib genotypes
• E (Y | p’)
E (Yj | pj)
•
•
•
•
For sib pair BB-Bb
x1j = m + a + e1j
x2j = m + d + e2j
Yj = (a + e1j - d - e2j)2 = (a - d + ej)2
E (Yj | pj)
pj
Genotype pair
Probability
0
BB - BB
p2(p2) = p4
1/2
1
BB - BB
BB - BB
2
3
2
2
p (p) = p
p (1) = p
E (Yj | pj)
Expectation
Variance components
E(Yj | pj = 1)
2
se
E(Yj | pj = 1/2)
s2e + s2a + 2s2d
E(Yj | pj = 0)
2
se
+
2
2s a
+
2
2s d
E (Yj | pj)
Yj
0
1/2
1
pj
E (Yj | pj)
• Expectation for Yj varies with proportion of pj
• E(Yj | pj) = a + bpj
a = (s2e + 2s2g)
b = -2s2g
pj = 0, 1/2, 1
• Note: s2d vanishes with large n
E(p’ | Im)
• Estimate p based on sib-pair and parental
genotypes for a marker locus
• fji is the probability that the jth sib pair have I
genes identical by descent
• Im is the information on sib-pair and parental
genotypes
• Our best estimate of pj (strongest correlation) is
given as
p’ = fj2 + 1/2fj1
 p’j is the Bayes estimate of pj when a squared
error loss function is used
• Maximum possible correlation with pj when pj is a
random variables taking on values of 1, 1/2, and 1
(Haseman, 1970).
E(p’ | Im)
Type
Probability
7 parental mating types
p(b)
34 offspring types
p(a|b)
Joint probability
p(ab)
E(p’ | Im)
Mating type Sib pair type p(ab) fj0
pi4
fj1
fj2
p' j
AiAi x AiAi
AiAi-AiAi
1/4 1/2 1/4 1/2
AiAi x AjAj
AiAj-AiAj
2pi2pj2 1/4 1/2 1/4 1/2
AiAi x AiAj
AiAi - AiAi
AiAi - AiAj
AiAj- AiAj
pi3pj
0 1/2 1/2 3/4
2pi3pj 1/2 1/2 0 1/4
pi3pj
0 1/2 1/2 3/4
For i = 0,1,2
Joint probability of observing Im
and that pj should equal i/2
fji =
S
S
P{v and w and pi = i/2},
2
S
S
ve Pp we Ps
S
h = 0 ve Pp we Ps
P{v and w and pj = h/2},
Sum of the three joint probabilities,
i = 0, 1, 2
E(Yj | p’j)
• Assume a two-allele marker locus...
• No dominance...
• And complete parental information
E(Y | p’)
• Given complete Im
• E(Yj|p’j) = a + bp’j
 b = -2(1-2c)2s2g
• (1-2c)2 = correlation between pjm and pjt,
i.e., proportion of marker genes ibd and
QTL genes i.b.d.
E(Yj|p’jm) =
S S
pjt pjm
E(Y|pjt)P{pjt|pjm}P{pjm|p’jm}
Joint distribution of pjt and pjm
Joint distribution of p’jm and pjm
E(Yj | p’jm) = [s2e + 2(1 - 2c + 2c2) s2g - 2(1 -c)2s2gp’jm
a = [s2e + 2(1 - 2c + 2c2)s2g
b = - 2(1 -c)2s2gp’jm
If c = 1/2, then b = 0
If c = 0, then b = -2s2g
A = marker
B = trait
P{pjm = pjt = 1} A1B1
A2B2
A1B1 (1 - c)/2
A2B2 (1 - c)/2
A1B2 c/2
A2B1 c/2
X
A3B3
A4B4
A3B3 (1 - c)/2
A4B4 (1 - c)/2
A3B4 c/2
A4B3 c/2
A3B3
A4B4
X
Sib 1
A1B1
A3B3
A1B1
A2B2
Sib 2
A1B1
A3B3
Sib 1
A1B1
A3B3
[(1 - c)/2]2
Sib 2
A1B1
A3B3
[(1 - c)/2]2
[(1 - c)/2]2[(1 - c)/2]2 = (1 - c)4 / 16
P{pjm = pjt = 1} =
4(c4/16) + 8[c2(1 - c)2 /16] + 4[(1 - c)4/ 16]
=[c2 + (1 - c)2]2/4 = y2 / 4,
where
y = c2 + (1 - c)2
Contemporary sib-pair analysis (Kruglyak
and Lander, 1995)
• Multipoint linkage analysis
– full inheritance information
– maximum likelihood estimates
• Qualitative traits
• Quantitative traits
Sib-pair analysis advantages
•
•
•
•
Sib pairs are relatively easy to ascertain
Closely matched, control for secular effects
No assumptions about inheritance
No assumptions:
– penetrance
– phenocopy
– disease allele frequency
Sib-pair analysis: Basic model
• Determine whether a sib pair shares 0, 1, or 2
alleles identical by descent (IBD)
• Affected sibs should share alleles IBD more often
than expected under random Mendelian
segregation (qualitative trait)
• Sib-pairs should show a correlation between
magnitude of phenotypic difference and number of
alleles shared IBD (quantitative trait)
Sib-pair analysis: Qualitative traits
• Estimated proportions of IBD sharing
– (z0, z1, z2)
• Mendelian expectation
 (a0, a1, a2) = (1/4, 1/2, 1/4)
• According to Holmans (1993):
– z0 + z1 + z2 = 1; 1/2  z1; z1  2z0
– If the is no dominance variance: z1 = 1/2
Sib-pair analysis and relative risk
(Risch, 1990)
• If only a single locus is involved...
• Relative-risk ratio for a sib (prevalence in
siblings of affecteds divided by population
prevalence)



lS = relative risk ratio for sibling
lO = relative risk ratio for offspring
lM = relative risk ratio for monozygotic twin
Sib-pair analysis and relative risk
(Risch, 1990)
•
•
•
•
zO = a0 / lS
z1 = a1lO / lS
z2 = a2lM / lS
In the absence of dominance variance,
lO = lS and lM - 1 = 2(lS - 1)
IBD distribution (adapted from Kruglyak and
Lander, 1995)
Sibling 1
4 2 3 2 3 2 3 4 4 1 3
2 3 4 5 5 4 3 3 3 1 2
Sibling 2
4 2 3 2 2 5 1 5 2 3 1
2 3 4 5 5 4 3 3 5 2 3
1.00
p(IBD)
p2
.50
0
p1
20
40
p0
60
80
100 cM
Quantitative trait sib-pair analysis
Let f1i, f2i denote phenotypes of two siblings
Di = f1i - f2i
vi represents the number of alleles shared IBD
At the QTL, variance of D depends on v
So that s20 > s21 > s22, where s2j is the
variance of the difference D when j alleles are
shared
• How do we test this hypothesis?
•
•
•
•
•
Quantitative traits with complete information:
Haseman-Elston
• E(Di2 | vi ) = a - bvi; b = s2g (additive genetic
variance)
• Linear regression assures an ML estimate only if
the noise process is normally distributed and
uncorrelated with the dependent variable
• Squared difference D2 does not necessarily follow
• Standard error and distribution of test statistic are
based on normal, uncorrelated error; thus, t-test
derived by dividing b by its standard error is
inappropriate
Quantitative traits with complete information:
ML QTL variance estimation
• Derive direct estimates of s2j based on D
for each value of v
• Assume the simple constraint
s20  s21  s22
• No dominance variance
s21 = (s20 + s22) / 2
• How to deal with incomplete data?
Quantitative traits with complete information:
Nonparametric QTL analysis
• Make no assumptions about the phenotypic
distribution; Wilcoxon rank-sum test
• Rank sib pairs according to absolute D;
rank(i) the rank of the ith sib pair and s a
location in the genome
n
XW(s) = S rank(i)  f(vi)
i=1
Quantitative traits with complete information:
Nonparametric QTL analysis
• For f(v)
• No linkage, XW(s) has expectation 0 and
variance V = [n(n+1)(2n+1)]/12
• Ratio Z(s) = XW(s) / V1/2
• Z(s) asymptotically distributed
– standard normal
– Ornstein-Uhlenbeck diffusion process
Lecture 5a: Mapping in humans (2 of 2)
• Linkage disequilibrium
• Allele frequency estimation
• Association analysis
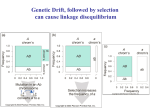
Linkage equilibrium and disequilibrium
• The linkage analyses so far discussed
assume linkage equilibrium
• All possible combination of alleles on a a
single chromosome (all possible haplotypes
or all possible gamete genotypes) occurs as
frequently as would be predicted from the
random association of individual allele
frequencies
For example, assume that:
A = 0.2 a = 0.8 M = 0.6 m = 0.4
Haplotypes
Expected
Frequency
AM
0.2 x 0.6
=
0.12
Am
0.2 x 0.4
=
0.08
aM
0.8 x 0.6
=
0.48
am
0.8 x 0.4
=
0.32
Total =
1.00
Disequilibrium =
D = observed frequency - expected frequency
Haplotype
Observed
l0 - lE
D
AM
.04
.04 - .12 =
-0.08
Am
.16
.16 - .08 =
+0.08
aM
.56
.58 - .48 =
+0.08
am
.24
.24 - .32 =
-0.08
Comments on linkage disequilibrium
• Dmax is determined by setting one of the haplotypes
involving the least common allele at a frequency of zero
– Dmax = 0.12, if frequency of AM were zero
– Absolute Dmax is 0.25 for any two-locus system
(frequency of each of four alleles were 0.25)
• Effect on linkage analysis
– If no assumptions about any genotype, D is not relevant
– Guess about one or more individual’s genotype, total
lod score is less accurate
Linkage disequilibrium between marker and
trait loci
• Most cases of trait are due to relatively few
distinct ancestral mutations at trait-causing
locus
• Allele A present on an ancestral chromosomes
and lying close enough to trait-causing locus so
that linkage has not been thoroughly “shuffled”
in the population’s history
• Young mutation in an isolated population
Association Studies
• Disregard familial patterns of inheritance
• Case-control studies
• Allele A is associated with a trait if it is
significantly more frequent among affecteds
as compared to unrelated controls
• 2 x 2 contingency c2 test
Association studies
• Choice of control group is a major issue
– Not an issue in linkage or allele-sharing method
– why?
• Association studies most meaningful when
it involves alleles with direct biological
relevance
Association studies and complex traits
• HLA complex (chrom. 6) implicated in etiology of
autoimmune diseases
• HLA-B27 allele
– Occurs in 90% of patients with ankylosing spondylities
– Only 9% of the general population
• Type I diabetes, rheumatoid arthritis, multiple
sclerosis, systemic lupus, late-onset Alzheimer’s
disease
Three competing hypotheses (Hn) for positive
associations
• H1: Allele is actually a cause of the disease
• H2: Allele is in linkage disequilibrium with the actual
cause (syntenic with trait-causing allele)
• Recall that for D
– Most cases of trait are due to relatively few distinct
ancestral mutations at trait-causing locus
– allele A was present on one of these ancestral
chromosomes and lies close enough to trait-causing
locus such that linkage has not been thoroughly
“shuffled” in the population’s history
– young mutation in an isolated population
Three competing hypotheses (Hn) for positive
associations
• H3: Artifact of population admixture
• A trait present at a higher frequency in an ethnic
group will be positively associated with any allele
that happens to be more common in tht group
• For example, (Lander and Shork, 1994)
– eating with chopstick in San Francisco
– HLA-A1 allele (more common among Asians
than Caucasians)