* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Gal - University of Rochester
Survey
Document related concepts
Transcript
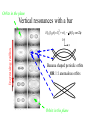
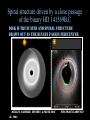
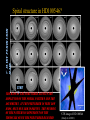
Alice Quillen University of Rochester Department of Physics and Astronomy May, 2005 Motivation—The Galactic Disk • The Milky Way has only rotated about 40 times (at the Sun’s Galacto-centric radius). No time for relaxation! • Structure in the motions of the stars can reveal clues about the evolution and formation of the disk. Coma Berenices • Little is known about the shape of the Galaxy disk • We can study our Galaxy star by star. • Prospect of radial velocity, proper motion, spectroscopic surveys of hundreds of millions of Galactic stars. Tangential velocity group Stellar velocity distribution Dehnen 98 Sirius group Pleiades group Hercules stream Radial velocity Hyades stream Low Perturbation Strengths • Spiral arms give a tangential force perturbation that is only ~5% of the axisymmetric component. Resonances allow a strong affect in only a few rotation periods 1 • Jupiter is 1000 the Mass of the Sun resonant effects or long timescales (secular) required Outline of Talk Resonances in the Solar neighborhood • Explaining moving groups • Chaos in the Solar neighborhood due to resonance overlap • Resonant trapping models for peanut shaped bulges Structure in circumstellar disks • Disk Edges, CoKuTau/4 • Spiral arms: HD141569A, HD100546 The amplitude of a pendulum will increase if resonantly forced The planet goes around the sun J times. The asteroid goes around K times. J:K mean motion resonance Perturbations add up only if they are in phase. Even small perturbations can add up over a long period of time. The Galactic Disk– Interpreting the U,V plane E Ecircular orbit Eepicyclic motion Orbit described by a guiding radius and an epicyclic amplitude Coma Berenices u -radial group Stellar velocity distribution Dehnen 98 velocity On the (u,v) plane the epicyclic amplitude is set by a2=u2/2+v2 The guiding or mean radius is set by v v tangential velocity (1 v)2 u 2 V02 ln r 2 2 Orbits associated with Lindblad resonance’s from a bar or spiral mode Location of Lindblad resonances is determined from the mean angular rotation rate Closer to corotation by the guiding or mean radius. On the (u,v) plane, as v changes, we expect to cross Lindblad Figure from Fux (2001) Simple Hamiltonian systems Harmonic oscillator p2 q 2 H( p, q) H ( I , ) I 2 2 H d is constant I dt H dI 0 I is conserved dt I p q Stable fixed point Libration Pendulum p2 H ( p , ) K cos( ) 2 Separatrix p Oscillation Structure V Weighting by the distance from closed orbits --similar to making a surface of section but this provides a weight on the u,v plane. Different angle offsets w.r.t the Sun The effect of different spiral waves on the local velocity distribution Different pattern speeds 2-armed log spirals U Each region on the u,v plane corresponds to a different family of closed/periodic orbits Near the 4:1 Lindblad resonance. Orbits excited by resonances can cross into the solar neighborhood A model consistent with Galactic structure Explains structure in the u,v plane Coma Berenices Pleiades group Hyades group Pleiades/Hyades moving groups support the spiral arms. Coma Berenices stars are out of phase. A model consistent with Galactic structure Explains structure in the u,v plane pattern 20km s-1kpc-1 Two dominant stellar arms – consistent with COBE/DIRBE model by Drimmel & Spergel (2001) Excites a 4 armed response locally We are at the 4:1 Inner Lindblad resonance This is a second order perturbation Nearing corotation Disk heating and other consequences Kink in shape of spiral arms predicted Flocculent structure past Sun In between resonances, the possibility of heating Oort’s constant and Epicyclic motion Zero’th order axi-symmetric Hamiltonian pr2 pz2 L2 H 0 ( pr , pz , L ; r , z , ) 2 0 ( r , z) 2 2r 2 I 1 I 2 I 3 aI 12 bI 22 cI1 I 2 ... Higher order terms I1 radial action ................. =epicyclic frequency (radial osc.) I 2 like angular momentum =angular rotation rate I 3 vertical action ................ =vertical oscillation frequency For discussion on action angle variables Contopoulos 1979, Dehnen 1999, and Lynden-Bell (1979) Adding a perturbation from a bar or spiral arm Perturbation to gravitational potential H1 ( pr , L , pz ; r , , z) Am (r , z)cos[m( pt )] for a bar mode Am cos[m( p t ) ln r ] for a logarithmic spiral mode, m arms Expand and take the dominant term In action angle variables: H1 ( I1 , I 2 , I 3 ; 1 , 2 , 3 ) I1 cos[1 m(2 pt )] near m : 1 ILR(inner Lindblad resonance) near m : 1 OLR(outer Lindblad resonance) Hamiltonian including a perturbation H 0 ( I 1 , I 2 ; 1 , 2 ) I 1 I 2 aI 12 bI 22 cI 1 I 2 I 11 / 2 cos[1 m(2 p t )] 1 m(2 pt ) is the resonant angle Canonical transformation H 0 ( J 1 , J 2 ; , 2 ) J 1 J 2 ( p ) a ' J 12 b ' J 22 c ' J 1 J 2 J 11 / 2 cos[ ] This is time independent, and J 2 is conserved. In phase space: Bar Mode angle on the plane R 2 I1 distance from origin Increasing radius H ( I 1, ) I 12 I 1 I 11 / 2 cos( ) Closed orbits correspond to fixed points •Outside OLR only one type of closed orbit. BAR •Inside OLR two types of closed orbits In phase space: Spiral-Mode Closed orbits correspond to fixed points Increasing radius •Inside ILR only one type of closed orbit. •Outside ILR two types of closed orbits Spiral arm supporting An additional perturbation can cause chaotic dynamics near a separatrix No separatrix Bifurcation of fixed point A separatrix exists Analogy to the forced pendulum Strength of first perturbation Strength of second perturbation H I12 I1 I11 / 2 cos I11 / 2 cos[ t ] Controls center of first resonance and depends on radius Controls spacing between resonances and also depends on radius Spiral structure at the BAR’s Outer Lindblad Resonance • Oscillating primarily with spiral structure • Perpendicular to spiral structure • Oscillating primarily with the bar • Perpendicular to the bar H I1 I 2 aI12 bI 22 cI1 I 2 s I11 / 2 cos[1 m(2 s t )] from spiral b I11 / 2 cos[1 m(2 b t )] from bar Poincare map used to look at stability. 2 Plot every t Orbits are either oscillating with both perturbations or are chaotic heating. Barred galaxies when seen edge-on display boxy/peanut shaped bulges Bureau et al. (1997) found that all boxy/peanut shaped bulges had evidence of noncircular orbits in their spectra. Boxy/peanut bulge No counter-examples of: •barred galaxies lacking boxy/peanut shaped bulges • non-barred galaxies displaying boxy/peanut shaped bulges. NGC 5746 From Bureau and Freeman 1997, PASA Previous Boxy/Peanut bulge formation mechanisms • Galaxy accretion (Binney & Petrou 1985) • Bar buckling (e.g., Raha et al 1991) also known as the fire-hose instability. • Diffusion about orbits associated with the 2:2:1 resonance (banana shaped orbit families) (e.g., Pfenniger & Friedli 1992, Combes et al. 1991) NGC 7582 1.6 μm Young bar From Quillen et al. 1995 A resonant trapping mechanism for lifting stars H 0 ( I 3,3 ) I 3 aI 32 H 1 ( x , z) f (r , z) cos[m( b t )] ' z2 cos[ m( b t )] I 3 cos 2 We chose second order in I 1 / 2 so that potential is symmetrical about plane m (2 b t ) resonant angle 2 Resulting Hamiltonian model 3 H ( I 3, ) I 32 I 3 I 2 cos 2 Orbits in the plane Vertical resonances with a bar Increasing radius H 0 ( I 3, ) I 32 I 3 (t )I 3 cos 2 Banana shaped periodic orbits OR 1:1 anomalous orbits Orbits in the plane Growing bar As the bar grows stars are lifted Resonance trapping Extent stars are lifted depends on the radius. A natural explanation for sharp edge to the peanut in boxy-peanut bulges. Starting from a stellar velocity distribution centered about planar circular orbits. Growing the perturbation in 3 rotation periods, resonance traps orbits (even though nonadiabatic growth). Extent of lifting is high enough to theoretically account for peanut thicknesses. Capture into vertical resonances • This new model suggests that peanuts grow simultaneously with bars (differing from other models). • We don’t know which resonance is dominant, but if we figure it out we may learn about the vertical shapes of galaxy bulges. • We used a symmetrical bar, however warp modes may be important during bar formation. • Formulism can also be used to address situations where the pattern speeds are changing, but are not well suited towards finding self-consistent solutions. In Summary: Galactic Disks Lindblad Resonances with a two-armed spiral density wave are a possible model for structure in the solar neighborhood velocity distribution. The pattern speed is s-1kpc-1 20km pattern Uncertainty mostly because of that in Oort’s constants. Interplay of different waves can cause localized heating, something to look for in observations. Constraints on properties of waves are possible. In Summary: Galactic Disks • Growth of structure can cause resonant trapping. A good way to constrain vertical structure of galaxy bulges... • So far no exploration of past history of galaxy! The way spiral waves grow should lead to different heating and capture and so different velocity distributions in different locations in the Galaxy. • Better tools coupled with forthcoming large Galactic surveys should tell us about growth and evolution of the Galactic disk. Spiral structure driven by a close passage of the binary HD 141569B,C Disk is truncated and spiral structure drawn out as the binary passes pericenter Quillen, Varniere, Minchev, & Frank 2005 al. 2003 STIS image Clampin et Flyby Pertruber Mass Spiral structure in HD100546? Time the perturber affects the The mass of amplitude of the spiral pattern and the asymmetry. If the perturber is very low mass, only one arm is driven. The winding of the pattern is dependent on the timescale since the perturber reached STIS image of HD 100546 (Grady et al 2001) Flybys and HD100546 • Morphology depends on how long since the flyby occurred. • However there is no candidate nearby star that could have been in the vicinity of HD100546 in the past few thousand years. • Furthermore, the probability that a star passed within a few hundred AU of HD 100546 is currently extremely low, presenting a problem for this scenario. Differences between flybys and a external bound perturber (binary): • Both stellar flybys and external planets can produce spiral structure. However external perturbers truncate disks and flybys tend to scatter the outer disk rather than truncate it. Long wavelength SEDs should be sensitive to the difference! • Both induce spiral structure that is more open with increasing radius and with increasing amplitude with increasing radius. In contrast to spiral density waves driven by an internal planet which becomes more tightly wound as a function of distance from the planet. Explaining spiral structure in HD100546 with a warped disk If viewed edge on would resemble Beta Pictorus Warps are long lasting –vary on secular timescales rather than rotation timescales Twist caused by precession of an initially tilted disk induced by a planet? Initial tilt caused by an interaction? Disk is too twisted to be explained with a single planet in the inner disk -> could be a Jupiter mass of bodies outside of 50AU