Download Gal - University of Rochester

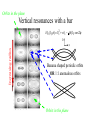
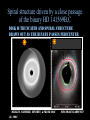
Alice Quillen
University of Rochester
Department of
Physics and Astronomy
May, 2005
Motivation—The Galactic Disk
• The Milky Way has only rotated about 40 times (at the
Sun’s Galacto-centric radius).
 No time for relaxation!
• Structure in the motions of the stars can reveal
clues about the evolution and formation of the disk.
Coma Berenices
• Little is known about the shape of the Galaxy disk
• We can study our
Galaxy star by star.
• Prospect of radial
velocity, proper
motion,
spectroscopic
surveys of
hundreds of
millions of Galactic
stars.
Tangential velocity
group
Stellar velocity distribution
Dehnen 98
Sirius group
Pleiades group
Hercules stream
Radial velocity Hyades stream
Low Perturbation Strengths
• Spiral arms give a tangential force perturbation that is
only ~5% of the axisymmetric component. Resonances
allow a strong affect in only a few rotation periods
1
• Jupiter is 1000 the Mass of the Sun
 resonant effects or long timescales (secular) required
Outline of Talk
Resonances in the Solar neighborhood
• Explaining moving groups
• Chaos in the Solar neighborhood due to resonance overlap
• Resonant trapping models for peanut shaped bulges
Structure in circumstellar disks
• Disk Edges, CoKuTau/4
• Spiral arms: HD141569A, HD100546
The amplitude of a pendulum will
increase if resonantly forced
The planet goes around the sun
J times.
The asteroid goes around
K times.
J:K mean motion resonance
Perturbations add up only if they
are in phase.
Even small perturbations can add
up over a long period of time.
The Galactic Disk–
Interpreting the U,V plane
E  Ecircular orbit  Eepicyclic motion
Orbit described by a
guiding radius and an
epicyclic amplitude
Coma Berenices
u -radial
group
Stellar velocity
distribution Dehnen 98
velocity
On the (u,v)
plane the
epicyclic
amplitude is
set by
a2=u2/2+v2
The guiding or
mean radius is
set by v
v tangential
velocity 
(1  v)2 u 2

  V02 ln r
2
2
Orbits associated with Lindblad resonance’s
from a bar or spiral mode
Location of
Lindblad
resonances is
determined from
the mean angular
rotation rate
Closer to corotation
 by the guiding
or mean radius.
On the (u,v) plane,
as v changes, we
expect to cross
Lindblad
Figure from Fux (2001)
Simple Hamiltonian systems
Harmonic oscillator
p2 q 2
H( p, q) 

 H ( I , )  I
2
2
H d

  is constant
I
dt
H
dI
   0 I is conserved

dt
I
p
q
Stable fixed point
Libration
Pendulum
p2
H ( p , ) 
 K cos( )
2
Separatrix

p
Oscillation

Structure
V
Weighting
by the
distance
from closed
orbits --similar to
making a
surface of
section but
this
provides a
weight on
the u,v
plane.
Different angle offsets w.r.t
the Sun
The effect of
different spiral
waves on the local
velocity
distribution
Different pattern speeds 2-armed log
spirals
U
Each region on the u,v plane corresponds to a
different family of closed/periodic orbits
Near the 4:1 Lindblad resonance. Orbits excited by
resonances can cross into the solar neighborhood
A model consistent with Galactic structure
Explains structure in the u,v plane
Coma Berenices
Pleiades group
Hyades group
Pleiades/Hyades moving groups support the spiral
arms.
Coma Berenices stars are out of phase.
A model consistent with Galactic structure
Explains structure in the u,v plane
 pattern  20km s-1kpc-1
Two dominant stellar arms – consistent with
COBE/DIRBE model by Drimmel & Spergel (2001)
Excites a 4 armed response locally We are at the
4:1 Inner Lindblad resonance
This is a second order perturbation
Nearing corotation

Disk heating and
other consequences
Kink in shape of
spiral arms
predicted
Flocculent
structure past Sun
In between
resonances, the
possibility of
heating
Oort’s constant and
Epicyclic motion
Zero’th order axi-symmetric Hamiltonian
pr2
pz2
L2
H 0 ( pr , pz , L ; r , z , ) 
 2 
  0 ( r , z)
2 2r
2
 I 1  I 2   I 3
 aI 12
 bI 22
 cI1 I 2  ...
Higher order terms
I1 radial action .................  =epicyclic frequency (radial osc.)
I 2 like angular momentum =angular rotation rate
I 3 vertical action ................  =vertical oscillation frequency
For discussion on action angle variables Contopoulos 1979, Dehnen 1999, and
Lynden-Bell (1979)
Adding a perturbation from a bar or
spiral arm
Perturbation to gravitational potential
H1 ( pr , L , pz ; r , , z)  Am (r , z)cos[m(   pt )]
for a bar mode
 Am cos[m(   p t )   ln r ]
for a logarithmic spiral mode, m arms
Expand and take the dominant term
In action angle variables:
H1 ( I1 , I 2 , I 3 ; 1 , 2 , 3 )   I1 cos[1  m(2   pt )]
 near m : 1 ILR(inner Lindblad resonance)
 near m : 1 OLR(outer Lindblad resonance)
Hamiltonian including a
perturbation
H 0 ( I 1 , I 2 ; 1 , 2 )  I 1  I 2 
 aI 12  bI 22  cI 1 I 2
  I 11 / 2 cos[1  m(2   p t )]
  1  m(2   pt ) is the resonant angle
Canonical transformation
H 0 ( J 1 , J 2 ;  , 2 )  J 1  J 2 (   p )
 a ' J 12  b ' J 22  c ' J 1 J 2   J 11 / 2 cos[ ]
This is time independent, and J 2 is conserved.
In phase space: Bar Mode

angle on the plane
R  2 I1 distance from origin
Increasing radius
H ( I 1, )  I 12   I 1   I 11 / 2 cos( )
Closed orbits correspond to fixed points
•Outside
OLR only
one type of
closed orbit.
BAR
•Inside OLR
two types of
closed orbits
In phase space: Spiral-Mode
Closed orbits correspond to fixed points
Increasing radius
•Inside ILR
only one
type of
closed orbit.
•Outside
ILR two
types of
closed orbits
Spiral arm supporting
An additional perturbation can cause
chaotic dynamics near a separatrix
No separatrix
Bifurcation of fixed point
A separatrix exists
Analogy to the forced pendulum
Strength of first
perturbation
Strength of second
perturbation
H  I12  I1   I11 / 2 cos    I11 / 2 cos[   t   ]
Controls center
of first resonance
and depends on
radius
Controls spacing
between
resonances and
also depends on
radius
Spiral structure at the
BAR’s Outer Lindblad
Resonance
• Oscillating primarily with spiral structure
• Perpendicular to spiral structure
• Oscillating primarily with the bar
• Perpendicular to the bar
H  I1  I 2   aI12  bI 22  cI1 I 2
  s I11 / 2 cos[1  m(2  s t )] from spiral
  b I11 / 2 cos[1  m(2  b t )] from bar
Poincare map used to look at stability.
2
Plot every
t 

Orbits are either oscillating with both perturbations
or are chaotic heating.
Barred galaxies when seen edge-on
display boxy/peanut shaped bulges
Bureau et al. (1997) found
that all boxy/peanut shaped
bulges had evidence of noncircular orbits in their spectra.
Boxy/peanut bulge
No counter-examples of:
•barred galaxies lacking
boxy/peanut shaped
bulges
• non-barred galaxies
displaying boxy/peanut
shaped bulges.
NGC 5746
From Bureau and Freeman 1997, PASA
Previous Boxy/Peanut bulge
formation mechanisms
• Galaxy accretion (Binney
& Petrou 1985)
• Bar buckling (e.g., Raha et
al 1991) also known as
the fire-hose instability.
• Diffusion about orbits
associated with the 2:2:1
resonance (banana shaped
orbit families) (e.g.,
Pfenniger & Friedli 1992,
Combes et al. 1991)
NGC 7582 1.6 μm
Young bar
From Quillen et al. 1995
A resonant trapping mechanism
for lifting stars
H 0 ( I 3,3 )  I 3  aI 32
H 1 ( x , z)  f (r , z) cos[m(  b t )]
  ' z2 cos[ m(  b t )]
  I 3 cos 2
We chose second order in I 1 / 2
so that potential is symmetrical about plane
m
(2  b t ) resonant angle
2
Resulting Hamiltonian model
  3 
H ( I 3, )  I 32   I 3   I 2 cos 2
Orbits in the plane
Vertical resonances with a bar
Increasing radius
H 0 ( I 3, )  I 32   I 3   (t )I 3 cos 2
Banana shaped periodic orbits
OR 1:1 anomalous orbits
Orbits in the plane
Growing bar
As the bar grows stars are lifted
Resonance trapping
Extent stars are lifted
depends on the radius.
A natural explanation for
sharp edge to the peanut
in boxy-peanut bulges.
Starting from a stellar velocity
distribution centered about
planar circular orbits.
Growing the perturbation in 3
rotation periods, resonance
traps orbits (even though nonadiabatic growth).
Extent of lifting is high
enough to theoretically
account for peanut
thicknesses.
Capture into vertical
resonances
• This new model suggests that peanuts
grow simultaneously with bars
(differing from other models).
• We don’t know which resonance is
dominant, but if we figure it out we may
learn about the vertical shapes of galaxy
bulges.
• We used a symmetrical bar, however
warp modes may be important during
bar formation.
• Formulism can also be used to address
situations where the pattern speeds are
changing, but are not well suited towards
finding self-consistent solutions.
In Summary: Galactic Disks
Lindblad Resonances with a
two-armed spiral density
wave are a possible model
for structure in the solar
neighborhood velocity
distribution.
The pattern
speed
is s-1kpc-1

 20km
pattern
Uncertainty mostly because
of that in Oort’s constants.
Interplay of different
waves can cause localized
heating, something to look
for in observations.
Constraints on properties
of waves are possible.
In Summary: Galactic Disks
• Growth of structure can cause resonant trapping. A good
way to constrain vertical structure of galaxy bulges...
• So far no exploration of past history of galaxy! The way
spiral waves grow should lead to different heating and
capture and so different velocity distributions in different
locations in the Galaxy.
• Better tools coupled with forthcoming large Galactic
surveys should tell us about growth and evolution of the
Galactic disk.
Spiral structure driven by a close passage
of the binary HD 141569B,C
Disk is truncated and spiral structure
drawn out as the binary passes pericenter
Quillen, Varniere, Minchev, & Frank 2005
al. 2003
STIS image Clampin et
 Flyby Pertruber
Mass
Spiral structure in HD100546?
Time
 the perturber affects the
The mass of
amplitude of the spiral pattern and the
asymmetry. If the perturber is very low
mass, only one arm is driven. The winding
of the pattern is dependent on the
timescale since the perturber reached
STIS image of HD 100546
(Grady et al 2001)
Flybys and HD100546
• Morphology depends on how long since the flyby occurred.
• However there is no candidate nearby star that could have been in the
vicinity of HD100546 in the past few thousand years.
• Furthermore, the probability that a star passed within a few hundred
AU of HD 100546 is currently extremely low, presenting a problem for
this scenario.
Differences between flybys and a external
bound perturber (binary):
• Both stellar flybys and external planets can produce spiral structure.
However external perturbers truncate disks and flybys tend to scatter
the outer disk rather than truncate it. Long wavelength SEDs should
be sensitive to the difference!
• Both induce spiral structure that is more open with increasing radius
and with increasing amplitude with increasing radius. In contrast to
spiral density waves driven by an internal planet which becomes more
tightly wound as a function of distance from the planet.
Explaining spiral structure in
HD100546 with a warped disk
If viewed edge on would resemble Beta Pictorus
Warps are long lasting –vary on secular
timescales rather than rotation timescales
Twist caused by precession of an initially tilted
disk induced by a planet? Initial tilt caused by an
interaction?
Disk is too twisted to be explained with a single
planet in the inner disk -> could be a Jupiter mass
of bodies outside of 50AU