* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 22 Electric Potential (Voltage)
Electromagnetism wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Field (physics) wikipedia , lookup
Lorentz force wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Potential energy wikipedia , lookup
Electric charge wikipedia , lookup
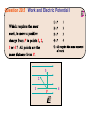
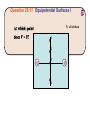
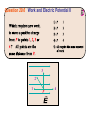
Chapter 22 Electric Potential (Voltage) Question 29.5 Work and Electric Potential I 3 2 1 P 4 Electric potential energy • Recall how a conservative force is related to the potential energy associated with that force: • The electric potential energy is the potential energy due to the electric force, which can be expressed in terms of the electric field. • If location A is chosen to be the zero point, then the electric potential at location B (which we now call r) is given by Potential energy of particle is a scalar function of space. Consider uniform electric field (say inside a parallel capacitor) If a proton is taken from location B to location C, how does its potential energy change? 1. it decreases 2. it increases 3. it doesn’t change Suppose a proton is released from rest just below the top (positive) plate of an parallel plate capacitor with an electric field strength E = 100 N/C. If the distance between the plates is d = 3 mm, how fast is it moving when it hits the bottom (negative) plate? Electric Potential (Voltage) • Electric potential, or voltage, is defined as the electric potential energy per unit charge a test particle would have if it were located at a position • Potential energy deals with the energy of a particle. Voltage deals with all locations in space (no particle needs to be there). • Analogous to how a particle experiences a force, but an electric field can exist at any point in space. • Electric Potential difference is defined as • Because the electrostatic field is conservative, it doesn’t matter what path is taken between those points. • In a uniform field, the potential difference becomes Question 29.4 Electric Potential Energy III Clicker Question In a parallel plate capacitor, the electric field is uniform and is directed from the positive plate to the negative plate. An electron goes from location A to location C. Which statement is true? A) The electron’s potential energy increases and it goes to a region of higher voltage. B) The electron’s potential energy decreases and it goes to a region of lower voltage. C) The electron’s potential energy increases and it goes to a region of lower voltage. Clicker question • The figure shows three straight paths AB of the same length, each in a different electric field. Which one of the three has the largest potential difference between the two points? A. (a) B. (b) C. (c) Electric potential of a point charge • The point-charge field varies with position, so we need to integrate: • Taking the zero of potential at infinity and letting gives Example Rutherford scattering. A helium nucleus of mass 4 mp is emitted with an initial speed of v0 = 4.9 x 105 m/s towards a gold nucleus of charge q2 = 79 e. What is the minimum distance between the two particles (assume the gold nucleus doesn’t move)? Electric potential of a charge distribution • If the electric field of the charge distribution is known, the electric potential can be found by integration. • The electric potential can always be found by summing point-charge potentials: • For discrete point charges, • For a continuous charge distribution, Clicker Question Potential of charged sphere • Outside sphere, electric field is identical to that of a point charge. Inside, E=0. • What is V for (r<R)? Maximum voltage of a Van de Graaff generator. • Molecules in air get ionized for electric fields greater than roughly Emax = 3 x 106 V/m. What is the maximum voltage of a charged sphere of radius R=0.2 m? Clicker Question Two identical positive charges of charge Q are a distance d apart. What is the voltage at the midway point between the charges? a) b) c) d) e) k Q/d 2 k Q/d 4 k Q/d 8 k Q/d 0 Question 29.11 Equipotential Surfaces I 5) all of them 1 2 +Q 3 4 –Q Clicker question Location P is equidistant from the two charges of an electric dipole. The voltage at P is a) positive b) zero c) negative CT 29.12c At which labeled point is voltage highest? B A D E C Electric potential of a charged ring • For a uniformly charged ring of total charge Q, integration gives the potential � on the ring axis: V = k dq r V (x, y, z) = dq = λadθ � 0 2π kλa dθ r(θ, x, y, z) • Very hard integral in general! If P is on x axis, then r is independent of θ. • Integrating the potentials of charged rings gives the potential of a uniformly charged disk: V (x) = � dQ k = r � 0 a λ2πr dr k √ x2 + r2 • This result reduces to the infinite-sheet potential close to the disk, and the point-charge potential far from the disk. Question 29.6 Work and Electric Potential II 3 2 1 P 4 Equipotentials • An equipotential is a surface on which the potential is constant. • In two-dimensional drawings, we represent equipotentials by curves similar to the contours of height on a map. • The electric field is always perpendicular to the equipotentials. (∆V = −E � · ∆�s = 0) Conductors • There’s no electric field inside a conductor in electrostatic equilibrium. • And even at the surface there’s no field component parallel to the surface. • Therefore it takes no work to move charge inside or on the surface of a conductor in electrostatic equilibrium. A conductor in electrostatic equilibrium is an equipotential. • The electric field must be perpendicular to the surface of a conductor (in electrostatic equilibrium Determining E from V? • Voltage can be determined if electric field is known • Can electric field be determined if voltage is known? � · ∆�r • For a very small displacement, ∆V = −E • Suppose ∆�r = ∆x î � · ∆�r = Ex ∆x Then E ∆V ∂V Ex = − =− ∆x ∂x Can do the same thing in other direction: � = −∇V = − E � ∂V ∂V ∂V î + ĵ + k̂ ∂x ∂y ∂z � The derivatives here are partial derivatives, expressing the variation with respect to one variable alone. (gradient of V) • For which region is the magnitude of the electric field the highest? 1. 2. 3. 4. 200 V 180 V A 160 V 140 V B 120 V 9 Distance (cm) 8 100 V 7 C 6 5 4 80 V D 3 2 1 1 2 3 4 5 6 Distance (cm) 7 8 9 10 A B C D CT 29.13b What is the approximate magnitude of the electric field at point A? (Each equipotential line is 2 m from the nearestneighbor equipotential.) A) 0.1 Volts/m B) 0.2 Volts/m C) 1.6 Volts/m D) 0.7 Volts/m E) None of these A 0V -1.4V -1.8V -2.1V