Download Lecture 23: Common Emitter Amplifier Frequency

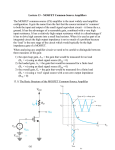
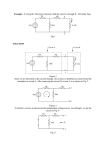
Whites, EE 320
Lecture 23
Page 1 of 18
Lecture 23: Common Emitter Amplifier
Frequency Response. Miller’s Theorem.
We’ll use the high frequency model for the BJT we developed in
the previous lecture and compute the frequency response of a
common emitter amplifier, as shown below in Fig. 10.9a.
(Fig. 10.9a)
(Fig. 10.1)
© 2016 Keith W. Whites
Whites, EE 320
Lecture 23
Page 2 of 18
As we discussed in the previous lecture, there are three distinct
region of frequency operation for this – and most – transistor
amplifier circuits. We’ll examine the operation of this CE
amplifier more closely when operated in three frequency
regimes.
Mid-band Frequency Response of the CE Amplifier
At the mid-band frequencies, the DC blocking capacitors are
assumed to have very small impedances so they can be replaced
by short circuits, while the impedances of C and C are very
large so they can be replaced by open circuits:
(Fig. 10.19a)
where RB  RB1 || RB 2 .
The equivalent small-signal model for the mid-band frequency
response is then
Whites, EE 320
Lecture 23
Page 3 of 18
We’ll define
RL  ro || RC || RL
(1)
Vo   g m RLV
(2)
so that at the output
Using Thévenin’s theorem followed by voltage division at the
input we find
r
r
RB
V 
VTH 
Vsig (3)

r  rx  RTH
r  rx  RB || Rsig RB  Rsig
Substituting (3) into (2) we find the mid-band voltage gain Am to
be
V
 g m r
RB

  ro || RC || RL  (10.54),(4)
Am  o 
Vsig r  rx  RB || Rsig RB  Rsig
High Frequency Response of the CE Amplifier
For the high frequency response of the CE amplifier of Fig.
10.19a, the impedance of the blocking capacitors is still
Whites, EE 320
Lecture 23
Page 4 of 18
negligibly small, but now the internal capacitances of the BJT
are no longer effectively open circuits.
Using the high frequency small-signal model of the BJT
discussed in the previous lecture, the equivalent small-signal
circuit of the CE amplifier now becomes:
(Fig. 10.19a)
We’ll simplify this circuit a little by calculating a Thévenin
equivalent circuit at the input and using the definition for RL in
(1):
(Fig. 10.19b)
where it can be easily shown that Vsig is V given in (3)
r
RB
Vsig 
Vsig

(Fig. 10.19b),(5)
r  rx  RB || Rsig RB  Rsig
while
Rsig  r ||  rx   RB || Rsig  
(Fig. 10.19b),(6)
Whites, EE 320
Lecture 23
Page 5 of 18
Miller’s Theorem
We can analyze the circuit in Fig. 10.19b through traditional
methods, but if we apply Miller’s theorem we can greatly
simplify the effort. Plus, it will be easier to apply an
approximation that will arise if we use Miller’s theorem.
You may have seen Miller’s theorem previously in circuit
analysis. It is another equivalent circuit theorem for linear
circuits akin to Thévenin’s and Norton’s theorems. Miller’s
theorem applies to this circuit topology:
(Fig. 1)
The equivalent Miller’s theorem circuit is
(Fig. 2)
where
Whites, EE 320
Lecture 23
ZA 
Zx
v
1 B
vA
and Z B 
Page 6 of 18
Zx
v
1 A
vB
(7),(8)
The equivalence of these two circuits can be easily verified. For
example, using KVL in Fig. 1
v A  i A Z x  vB
v v
iA  A B
or
(9)
Zx
while using KVL in the left-hand figure of Fig. 2 gives
v
iA  A
(10)
ZA
Now, for the left-hand figure to be equivalent to the circuit in
Fig. 1, then iA in (9) and iA in (10) must be equal. Therefore,
v A  vB v A

Zx
ZA
The equivalent impedance ZA can be obtained from this equation
as
Zv
Zx
ZA  x A 
v A  vB 1  vB
vA
which is the same as (7). A similar result verifies (8).
So, for a resistive element Rx, Miller’s theorem states that
Whites, EE 320
Lecture 23
Page 7 of 18
Rx
Rx
and RB 
(12),(13)
vB
vA
1
1
vA
vB
while for a capacitive element Cx, Miller’s theorem states that
 v 
 v 
C A  C x 1  B  and CB  Cx 1  A  (14),(15)
 vA 
 vB 
RA 
High Frequency Response of the CE Amplifier (cont.)
Returning now to the CE amplifier equivalent small-signal
circuit of Fig. 10.19b, we’ll apply Miller’s theorem of Figs. 1
and 2 to this circuit and the capacitor C to give
(Fig. 3)
where, using (14) and (15),
 V 
 V 
C A  C 1  o  and CB  C 1   
 V 
 Vo 
(16),(17)
Whites, EE 320
Lecture 23
Page 8 of 18
Actually, this equivalent circuit of Fig. 3 is no simpler to
analyze than the one in Fig. 10.19b because of the dependence
of CA and CB on the voltages Vo and V.
However, this equivalent circuit of Fig. 3 will prove valuable for
the following approximation. Note from Fig. 10.19b that
I L  I   g mV  I L  g mV  I 
(18)
Up to frequencies near fH and better, the current I in the small
capacitor C will be much smaller than g mV . Consequently,
from (18)
(19)
I L  g mV
and
Vo   I L RL   g m RLV
(20)
Using this last result in (16) and (17) we find that
 g R V 
C A  C 1  m L    C 1  g m RL


V





V
1 
and
C B  C  1 
  C  1 

 g R V 
 g R
m L  
m L 




(21)
(22)
Most often for this type of amplifier, g m RL  1 so that in (22)
CB  C . But as we initially assumed, the current through C is
much smaller than that through the dependent current source
g mV , which ultimately led to equation (19).
Whites, EE 320
Lecture 23
Page 9 of 18
Consequently, we can ignore CB in parallel with g mV and the
final high frequency small-signal equivalent circuit for the CE
amplifier in Fig. 10.19a is
(Fig. 10.19c)
where

Cin  C  C A  C  C 1  g m RL

(Fig. 10.19c),(22)
Based on this small-signal equivalent circuit, we’ll derive the
high-frequency response of this CE amplifier. At the input
Z Cin
V 
Vsig
(23)

Z Cin  Rsig
while at the output
Vo   g m RLV
(24)
Substituting (23) into (24) gives
Vo   g m RL
Z Cin
Z Cin
 Rsig
Since Z Cin   jCin  then (25) becomes
1
Vsig
(25)
Whites, EE 320
Vo   g m RL
Lecture 23
1
jCin
1
 Rsig
jCin
Vsig 
Page 10 of 18
 g m RL
1  jCin Rsig
Vsig
(26)
If we define
H 
1
Cin Rsig
then substitute this into (26) gives
Vo
 g m RL  g m RL



f
Vsig 1  j
1 j
H
fH

1
fH  H 
where
2 2 Cin Rsig
(27)
(28)
(10.57),(29)
You should recognize this transfer function (28) as that for a low
pass circuit with a cut-off frequency (or 3-dB frequency) of H.
This is the response of a single time constant circuit, which is
what we have at the input to the circuit of Fig. 10.19c.
What we’re ultimately interested in is the overall transfer
function Vo Vsig from input to output. This can be easily derived
from the work we’ve already done here. Since
Vo
Vo Vsig

(30)
Vsig Vsig Vsig
Whites, EE 320
Lecture 23
Page 11 of 18
We can use (28) for the first term in the RHS of (30), and use (5)
for the second giving
Vo
r
 g m RL
RB
(31)



f
Vsig 1  j
r  rx  RB || Rsig RB  Rsig
fH
We can recognize Am from (4) in this expression giving
Vo
Am

(10.56),(32)
f
Vsig 1  j
fH
Once again, this is the frequency response of a low pass circuit,
as shown below:
(Fig. 10.19d)
Comments and the Miller Effect
 Equation (32) gives the mid-band and high frequency
response of the CE amplifier circuit. It is not valid for the low
Whites, EE 320
Lecture 23
Page 12 of 18
frequency response near fL and lower frequencies, as shown in
Fig. 5.71b.
 The high frequency, small-signal equivalent circuit models for
the BJT in a common emitter amplifier are:
 It turns out that Cin in (22) is usually dominated by
C A  C 1  g m RL . Even though C is usually much smaller
than C its effects at the input are accentuated by the factor
1  g m RL .


 The reason that C undergoes this multiplication is because it
is connected between two nodes (B’ and C in Fig. 10.19a) that
experience a large voltage gain. This effect is called the
Miller effect and the multiplying factor 1  g m RL in (22) is
called the Miller multiplier.
Whites, EE 320
Lecture 23
Page 13 of 18
 Because of this Miller effect and the Miller multiplier, the
input capacitance Cin of the CE amplifier is usually quite
large. Consequently, from (20) the fH of this amplifier is
reduced. In other words, this Miller effect limits the high
frequency applications of the CE amplifier because the
bandwidth and gain will be limited.
Low Frequency Response of the CE Amplifier
On the other end of the spectrum, the low frequency response of
the CE amplifier – and all other capacitively coupled amplifiers
– is limited by the DC blocking and bypass capacitors.
This type of low frequency response analysis is rather
complicated because there is more than a single time constant
response involved. In the circuit of Fig. 10.9a there are three
capacitors involved, CC1, CC2, and CE. All three of these greatly
affect the low frequency response of the amplifier and can’t be
ignored.
The text presents an approximate solution in which the low
frequency response is modeled as the product of three high pass
single time constant circuits cascaded together so that

Vo
j 
j 
j 
(33)
  Am 






Vsig
 j   p1  j   p 2  j   p 3 
Whites, EE 320
Lecture 23
Page 14 of 18
(Fig. 10.7)
So there isn’t a single fL as suggested by Fig. 10.1 but rather a
more complicated response at low frequencies as we see in Fig.
10.7 above. Computer simulation is perhaps the best predictor
for this complicated frequency response, but an approximate
formula for fL is given in the text as
1  1
1
1 
f L  f p1  f p 2  f p 3 




2  CC1RC1 CE RE CC 2 RC 2 
(10.20),(34)
where RC1 , RE , and RC 2 are the resistances seen by CC1 , CE , and
CC 2 , respectively, with the signal source Vsig  0 and the other
two capacitors replaced by short circuits.
Example N23.1. Compute the mid-band small-signal voltage
gain and the upper 3-dB cutoff frequency of the small-signal
voltage gain for the CE amplifier shown in Fig. 10.9a. Use a
2N2222A transistor and the circuit element and DC source
values listed in text Example 10.4. Use 10 F blocking and
bypass capacitors.
Whites, EE 320
Lecture 23
Page 15 of 18
The circuit in Agilent Advanced Design System appears as:
V_DC
SRC2
Vdc=10.0 V
AC
AC
AC1
Start=100 Hz
Stop=1.0 MHz
Step=100 Hz
R
R2
R=8 kOhm
vo
C
C2
C=10 uF
vi
V_AC
R
SRC1
R3
Vac=polar(1,0) V R=5 kOhm
Freq=freq
C
C1
C=10 uF
R
R4
R=5 kOhm
R
R1
R=100 kOhm ap_npn_2N2222A_19930601
Q1
C
I_DC
C3
SRC4
Idc=1 mA C=10 uF
V_DC
SRC3
Vdc=-10.0 V
From the results of the ADS circuit analysis
VCB  2.03 V   400 mV   2.43 V
VBE  0.4 V   1.02 V   0.62 V
From Fig. 9 in the Motorola 2N2222A datasheet (see the
previous set of lecture notes)
 For VCB  2.43 V  Ccb  C  5.8 pF.
 For VBE  0.62 V  Ceb  C  20 pF.
Whites, EE 320
gm 
Lecture 23
Page 16 of 18
IC
1 mA

 0.04 S
VT 25 mV
The unity gain frequency, fT, is a hugely important high
frequency specification for a transistor. fT (or T) is the
frequency at which the gain of the transistor operating as an
amplifier is one (0 dB):
From (10.41),
fT 
gm
0.04

 246.8 MHz
2  C  C  2  20 pF  5.8 pF 
This value agrees fairly well with the datasheet value of 300
MHz.
 0  265 from the ADS parts list for this 2N2222A transistor.
Therefore,
r 
0
gm

265
 6,625 
0.04
Whites, EE 320
Lecture 23
Page 17 of 18
From the 2N2222A datasheet, the nominal output resistance at
IC = 1 mA is ro  50 k.
What about rx? It’s so small in value (~ 50 ) that we’ll easily
be able to ignore it for the Am calculations compared to r (which
is 6,625  as we just calculated). From (4),
 g m r
RB
Am 

  ro || RC || RL 


r  rx  RB || Rsig RB  Rsig 
 


2,898.6  RL
0.02327
V
V
Am   36.2 dB
Am  64.24
Therefore,
or in decibels
0.9524
Am  20 log10 
From ADS:
m3
freq= 400.0 Hz
dB(vo)=33.632
40
dB(vo)
35
m3
m1
m2
freq= 6.300kHz freq= 84.40kHz
dB(vo)=36.053 dB(vo)=33.046
m1
m2
30
25
20
15
10
1E2
1E3
1E4
freq, Hz
1E5
1E6
Whites, EE 320
Lecture 23
Page 18 of 18
From this plot, ADS computes a mid-band gain of Am  36.05
dB, which agrees closely with the predicted value above.
fH 
From (29),
where from (22)

1
2 Cin Rsig

Cin  C  C 1  g m RL  20  5.8 1  0.04  2,898.6  pF
 20  678.3  698.3 pF
while from (6)
Rsig  r ||  rx   RB || Rsig  
Because RB || Rsig  100 k || 5 k  4,761.9  is so much larger
than rx (on the order of 50 ), we can safely ignore rx. Then,
Rsig  6,625 || 4,762  2,771 
Therefore,
f H  2  698.3  1012  2,771  82.25 kHz
This agrees very closely with the value of 84.40 kHz predicted
by the ADS simulation shown above. Notice that this frequency
is dramatically smaller than the unity-gain frequency of the
transistor fT  250 MHz.
[Add a short discussion on the gain-bandwidth product Am f H .]