Download Lecture 31: MON 30 MAR Review Session : Midterm 3

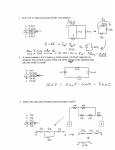
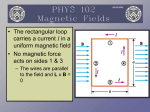
Physics 2113
Jonathan Dowling
Lecture 31: MON 30 MAR
Review Session : Midterm 3
EXAM 03: 8PM MON 30 MAR in Cox Auditorium The exam will cover: Ch.26 through Ch.29
The exam will be based on: HW07 – HW10. The formula sheet for the exam can be found here:
http://www.phys.lsu.edu/classes/fall2014/phys2113/downloads/FormulaSheetTest3.pdf
You can see examples of old exam IIIs here:
http://www.phys.lsu.edu/faculty/gonzalez/Teaching/Phys2102/Phys2102OldTests/
Current and Resistance
i = dq/dt
Junction rule
R = ρL/A
r = ρ0(1+a(T-T0))
V=iR
E=Jρ
Current and Resistance
Current and Resistance: Checkpoints, Questions
A cylindrical resistor of radius 5.0mm and
length 2.0 cm is made of a material that has a
resistivity of 3.5x10-5 Ωm. What are the (a)
current density and (b) the potential difference
when the energy dissipation rate in the resistor
is 1.0W?
Circuits
i = dq/dt
Junction rule
DC Circuits
Loop rule
V = iR
P = iV
Single loop
Multiloop
Resistors vs Capacitors
Resistors
Key formula: V=iR
Capacitors
Q=CV
In series: same current
Req=∑Rj
same charge
1/Ceq= ∑1/Cj
In parallel: same voltage
1/Req= ∑1/Rj
same voltage
Ceq=∑Cj
Resistors
in Series and in Parallel
•  What’s the equivalent resistance?
•  What’s the current in each resistor?
•  What’s the potential across each resistor?
•  What’s the current delivered by the battery?
•  What’s the power dissipated by each resisitor?
Series and Parallel Series and Parallel Series and Parallel Circuits: Checkpoints, Questions
Problem: 27.P.018. [406649]
Figure 27-33 shows five 5.00 resistors.
(Hint: For each pair of points, imagine that a battery is connected
across the pair.)
Fig. 27-33
(a) Find the equivalent resistance between points F and H.
(b) Find the equivalent resistance between points F and G.
Slide Rules: You may bend the wires but not break them. You may slide any circuit element along a
wire so long as you don’t slide it past a
three (or more) point junction or another
circuit element. Problem: 27.P.046. [406629]
In an RC series circuit, E = 17.0 V, R = 1.50 MΩ, and C =
1.80 µF.
(a) Calculate the time constant.
(b) Find the maximum charge that will appear on the
capacitor during charging.
(c) How long does it take for the charge to build up to 16.0
µC?
Magnetic Forces and Torques
v
mv
!
!
!
r
=
!
F
qB
F = qv ×B + q E
!
! !
dF = i dL × B
! ! !
τ = µ×B
L
Top view
τ net = iAB sin θ
Side view
CFnet = 0
C
Magnetic Torque on a Current Loop
Consider the rectangular loop in fig. a with sides of lengths a and b and that carries
a current i. The loop is placed in a magnetic field so that the normal nˆ to the loop
!
forms an angle θ with B. The magnitude of the magnetic force on sides 1 and 3 is
F1 = F3 = iaB sin 90° = iaB. The magnetic force on sides 2 and 4 is
F2 = F4 = ibB sin(90 − θ ) = ibB cos θ . These forces cancel in pairs and thus Fnet = 0.
The torque about the loop center C of F2 and F4 is zero because both forces pass
through point C. The moment arm for F1 and F3 is equal to (b / 2) sin θ . The two
torques tend to rotate the loop in the same (clockwise) direction and thus add up.
The net torque τ = τ 1 +τ 3 =(iabB / 2) sin θ + (iabB / 2) sin θ = iabB sin θ = iAB sin θ .
(28-13)
!
! !
Magnetic Dipole Moment
τ = µ×B
The torque of a coil that has N loops exerted
! !
U = −µ ⋅ B
by a uniform magnetic field B and carries a
current i is given by the equation τ = NiAB.
!
We define a new vector µ associated with the coil,
which is known as the magnetic dipole moment of
U = µB
U = −µ B
the coil.
The magnitude of the magnetic dipole moment is µ = NiA.
Its direction is perpendicular to the plane of the coil.
!
The sense of µ is defined by the right-hand rule. We curl the fingers of the right hand
in the direction of the current. The thumb gives us the sense. The torque can be
!
!
expressed in the form τ = µ B sin θ where θ is the angle between µ and B.
! ! !
In vector form: τ = µ × B.
! !
The potential energy of the coil is: U = − µ B cos θ = − µ ⋅ B.
U has a minimum value of − µ B for θ = 0 (position of stable equilibrium).
U has a maximum value of µ B for θ = 180° (position of unstable equilibrium).
Note : For both positions the net torque is τ = 0.
(28-14)
Ch 28: Checkpoints and Questions
Circular Motion:
v
F
r
B into blackboard.
Since magnetic force is perpendicular to motion,
the movement of charges is circular.
2
v
out
2
Fcentrifugal = ma = mrω = m
r
in
magnetic
F
= qvB
FB = FC
mv 2
→ qv B =
r
mv
Solve : r =
qB
In general, path is a helix (component of v parallel
to field is unchanged).
!
v
!
F
C
.
r
. B!
mv
r=
qB
Radius of Circlcular Orbit
v qB
ω= =
r m
Angular Frequency:
Independent of v electron
2πr 2πmv 2πm
T≡
=
=
v
qBv
qB
1
qB
f ≡ =
T 2πm
Period of Orbit:
Independent of v Orbital Frequency:
Independent of v Problem: 28.P.024. [566302]
In the figure below, a charged particle moves into a region of uniform
magnetic field , goes through half a circle, and then exits that region. The
particle is either a proton or an electron (you must decide which). It
spends 160 ns in the region.
(a) What is the magnitude of B?
(b) If the particle is sent back through the magnetic field (along the same
initial path) but with 3.00 times its previous kinetic energy, how much
time does it spend in the field during this trip?
!
F = iLBsin θ
!
τ = µ Bsin θ
= − µ B cosθ
!
µ
!
µ
B
Highest Torque:
θ = ±90° sinθ = ±1
Lowest Torque:
θ= 0° & 180° sinθ = 0
θ = 180°
–cosθ = +1
θ = 0°
–cosθ = –1
Right Hand Rule: Given Current i Find Magnetic Field B Checkpoints/Questions
Magnetic field?
Force on each wire due to
currents in the other wires?
Ampere’s Law: Find Magnitude of ∫B·ds?
Right Hand Rule: Given Current i Find Magnetic Field B A
C
y
l
P
x
z
B
+z is out of page
D
A
BB
BA
BD
BC
BB,C
BD
BA
BD
BA
BB,C
BB,C
BA
BD
BA
BD
BB,C
C
y
The current
in wires
A,B,D is out of the
l
P
page, current in C is into the page.
Each wire
x
z
produces a circular field+z line
going through
is out of page
B
D
P, and the direction of the magnetic field for
each is given by the right hand rule. So, the
circles centers in A,B,D
B
B are
counterclockwise, the circle centered at C is
clockwise. When Byou Bdraw the arrows at the
point P, the fields BfromB B and C are pointing
in the same direction (up and left).
B
A
D
C
B,C
D
BA
BD
Right Hand Rule & Biot-Savart: Given i Find B A length of wire is formed into a closed circuit with radii a and b, as
shown in the Figure, and carries a current i.
(a) What are the magnitude and direction of B at point P?
B=
(b) Find the magnetic dipole moment of the circuit.
µ 0 iφ
4πR
!
B=⊗
µ=NiA