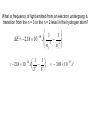* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Powerpoint handout
Quantum dot wikipedia , lookup
Coherent states wikipedia , lookup
Quantum computing wikipedia , lookup
Ferromagnetism wikipedia , lookup
Quantum machine learning wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Tight binding wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Matter wave wikipedia , lookup
Quantum key distribution wikipedia , lookup
Quantum teleportation wikipedia , lookup
Double-slit experiment wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Quantum group wikipedia , lookup
Renormalization wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
EPR paradox wikipedia , lookup
Canonical quantization wikipedia , lookup
History of quantum field theory wikipedia , lookup
Particle in a box wikipedia , lookup
Quantum state wikipedia , lookup
Hidden variable theory wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Wave–particle duality wikipedia , lookup
Atomic orbital wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Electron configuration wikipedia , lookup
The Bohr Model of the Atom
The behavior of electrons in atoms is revealed by
the light given off when the electrons are “excited”
(made to absorb energy).
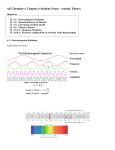
Johann Balmer showed that the visible series of lines from
the hydrogen spectrum obeyed the formula:
1
1
(or ) 2 2 for n 3, 4, 5....
2
n
1
Niels Bohr explained all the various lines by
proposing that electrons in atoms could have only
certain energies, and that light was given off when
an electron underwent a transition from a higher
energy level to a lower one.
This leads to the following picture of what is
happening:
Bohr derived a more general formula to predict the
observed energies of light:
Each electron’s energy is determined by which level
it is in. The levels are designated by whole numbers, n.
1
E k 2
n
The energy cannot take any value, but has only
certain values depending on n.
Then for a change from one level to another,
the energy difference can be calculated:
What is frequency of light emitted from an electron undergoing a
transition from the n = 3 to the n = 2 level in the hydrogen atom?
1
1
E 2.18 10 18 J 2 2
n
n
f
i
2.18 10
18
1
1
J 2 2
2
3
3.03 10 19 J
Find the frequency of this light:
E
h
3.03 10 19 J
6.63 10 34 J s
4.57 1014 s 1
Find the wavelength of this light:
c
300
. 108 m / s
4.57 10 s
6.54 10 7
14
1
6.54 10 7 m
10 9 nm
m
654 nm
1m
Now, for what really happens. . .
For atoms with >1 electron, we must use a more complete
theory.
This theory, known as quantum mechanics, has more
quantum numbers than just n. Each electron is
characterized by n, and three other quantum numbers.
Here are the quantum numbers, and the values they can take:
n = 1, 2, 3 . . . (Principal quantum number)
l = 0, 1, 2 . . . (n – 1)
(Angular momentum quantum number)
(Determines shape of orbit)
ml = -l . . . . +l
(Magnetic quantum number)
(Determines orientation)
ms = +½ or -½
(Spin quantum number)
The energy and location of each electron in an atom is
determined by these numbers. Each electron has one
set: {n, l, ml, ms}.
Pauli exclusion principle:
Each electron in an atom must have a unique set of
the four quantum numbers.