Download slides introducing IR/Raman of proteins

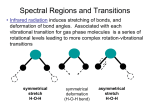
Light (E-M Radiation) Characteristics
• Frequency matches change in energy, type of motion
E = hn, where n = c/l (in sec-1 or Hz)
• Intensity increases the transition probability— Absorbance
I ~ e2 –where e is the Electric Field strength in the radiation
• Absorbance is ratio A = -log(I/Io)
• Linear Polarization aligns to direction of dipole change
A ~ [dm/dQ]2 where Q is the coordinate of the motion
Circular Polarization results from an interference:
R ~ Im(m • m) m and m are electric and magnetic dipole
1.2
Absorbance
A
IR of an oil
C-H
C=O
C-C
.8
CH2
.4
hn
0
4000
3000
2000
Frequency (cm -1 )
1000
Spectral Regions and Transitions
Magnetic Resonance—different course
• Long wavelength radiowaves are of low energy that is
sufficient to ‘flip’ the spin of nuclei in a magnetic field (NMR).
Nuclei interact weakly so spectral transitions between single,
well defined energy levels are very sharp and well resolved.
NMR is a vital technique for biological structure studies.
• Higher energy microwaves can promote changes in the
rotational motions of gas phase molecules, which is the basis
of microwave rotational spectroscopy (not a method of
biological importance).
• Microwaves are also used for spin-flips of electrons in
magnetic fields (ESR or EPR), important for free radicals and
transition metal systems (open shell). Magnetic dipole
coupling can be used to measure distances between spins—
growing importance in peptides and proteins.
Spectral Regions and Transitions
• Infrared radiation excites molecular vibrations, i.e.
stretching of bonds and deformation of bond angles.
Molecule has 3N-6 internal degrees of freedom, N
atoms. States characterize the bound ground state.
• Radiation in the visible (Vis) and ultraviolet (UV) regions
, will excite electrons from the bound (ground) state to
more weakly bound and dissociative (excited) states.
• Changes in both the vibrational and rotational states of
the molecule can be associated with this, causing the
spectra to become broadened or have fine structure.
Spectroscopic Process
• Molecules contain distribution of charges (electrons and
nuclei, charges from protons) which is dynamically changed
when molecule is exposed to light
• In a spectroscopic experiment, light is used to probe a
sample. What we seek to understand is:
– the RATE at which the molecule responds to this
perturbation (this is the response or spectral intensity)
– why only certain wavelengths cause changes (this is the
spectrum, the wavelength dependence of the response)
– the process by which the molecule alters the radiation
that emerges from the sample (absorption, scattering,
fluorescence, photochemistry, etc.) so we can detect it
Spectral Regions and Transitions
• Infrared radiation induces stretching of bonds, and
deformation of bond angles. Associated with each
vibrational transition for gas phase molecules is a series of
rotational levels leading to more complex rotation-vibrational
transitions
symmetrical
stretch
H-O-H
symmetrical
deformation
(H-O-H bend)
asymmetrical
stretch
H-O-H
Vibrational States and Transitions
• The simplest case is a diatomic molecule. Rotations (2) and
translations (3) leave only one vibrational degree of
freedom, the bond length change, Dr, a one dimensional
harmonic oscillator
• One can solve this problem exactly as a classical Hook’s
law problem with
– a restoring force: F = –kDr
and
– potential energy: V=1/2 k(Dr)2
• Quantum mechanically: Ev = (v+1/2)hn ,
 n is the vibration frequency
Harmonic Oscillator
Model for vibrational spectroscopy
E
re
r
e
q
v=3
5 hn
2
3 hn
2
1hn
2
v=2
v=1
Ev = (v+½)hn
IR
v=0
Dv =  1
DE = hn
n = (1/2p)(k/m)½
Raman
9hn
2
7
hn
2
v=4
r
(virtual
state)
hn
re
Vibrational States and Transitions
for the simplest harmonic oscillator case (diatomic):
n = (1/2p)(k/µ)1/2 where k is the force constant (d2V/dq2).
– In practice, stronger bonds have sharper (more curvature)
potential energy curves, result: higher k, and higher
frequency.
and µ is the reduced mass [m1m2 / (m1+m2)].
– In practice, heavier atom moving, have lower frequency.
 vibrational frequencies reflect structure, bonds and atoms
Vibrational States and Transitions
• Summary: high mass ==>
low frequency
strong bond ==> high frequency
• Some simple examples (stretches in polyatomics):
-C-C- ~1000 cm-1
C-H
~2800 cm-1
-C=C- ~1600 cm-1
C-D
~2200 cm-1
-C  C- ~2200 cm-1
C---N
~1300 cm-1
Polyatomic Vibrational States
• For a molecule of N atoms, there are (3N-6) vibrational degrees
of freedom. This complex problem can be solved the harmonic
approximation by transforming to a new set of normal
coordinates (combinations of internal coordinates, qi) to simplify
the potential energy V—method unimportant for this course
V = V0 + S (dV/dqi)0qi + (½) S (d2V/dqiqj)0qiqj + . . . . .
• This results in a molecular energy that is just the sum of the
individual vibrational energies of each normal mode:
E = S Ei = S (vi + ½) hni
• As a result we have characteristic IR and Raman frequencies,
ni, which are reflect bond types in the molecule. The frequency
pattern forms a “fingerprint” for the molecule and its structure.
• Variations due to conformation and environment give structural
insight and are the prime tools for Protein IR and Raman.
Dipole Moment
• Interaction of light with matter can be described as the
induction of dipoles, mind , by the light electric field, E:
mind = a . E
where a is the polarizability
• IR absorption strength is proportional to
A ~ |<Yf |m| Yi>|2, transition moment between Yi Yf
• To be observed in the IR, the molecule must change its
electric dipole moment, µ , in the transition—leads to
selection rules
dµ / dQi  0
• Raman intensity is related to the polarizability,
I ~ <Yb |a| Ya>2, similarly da / dQi  0 for Raman
observation
IR vs. Raman Selection Rules
• At its core, Raman also depends on dipolar interaction,
but it is a two-photon process, excite with n0 and detect ns,
where nvib = n0 - ns, so there are two m’s.
<Y0|m| Yi> • <Yi|m| Yn> ~ a
=> need a change in POLARIZABILITY for Raman effect
n
0
nvib = nn- n0 = DE / h
n0
ns
i
n
0
nvib = n0- ns
Symmetry Selection Rules (Dipole, etc.)
Example:
symmetric stretch
O=C=O
asymmetric stretch
O=C=O
infrared active
dm/dQ  0
bending
O=C=O
infrared active
dm/dQ  0
infrared inactive dm/dQ = 0
Raman Intense
da/dQ  0
Complementarity: IR and Raman
IR
Raman
If molecule is centrosymmetric, no overlap of IR and Raman
Vibrational Transition Selection Rules
Harmonic oscillator: only one quantum can change on each
excitation D vi = ± 1, D vj = 0; i  j .
These are fundamental vibrations
Anharmonicity permits overtones and combinations
Normally transitions will be seen from only vi = 0, since most
excited states have little population.
Population, ni, is determined by thermal equilibrium, from the
Boltzman relationship:
ni = n0 exp[-(Ei-E0)/kT],
where T is the temperature (ºK) – (note: kT at room temp
~200 cm-1)
Anharmonic Transitions
Real molecules are anharmonic to some degree so other transitions do
occur but are weak. These are termed overtones (D vi = ± 2,± 3, . .) or
combination bands (D vi = ± 1, D vj = ± 1, . .).
E/De
D0
DE01 = hnanh
( r - re )/re
Biological systems we generally overlook this, most important in C-H stretch region
Peak Heights
• Beer-Lambert Law:
• A = elc
–
–
–
–
A = Absorbance
e = Absorptivity
l = Pathlength
c = Concentration
An overlay of 5 spectra of Isopropanol (IPA) in water. IPA Conc.
varies from 70% to 9%. Note how the absorbance changes with
concentration.
• The size (intensity) of absorbance bands depend upon molecular
concentration and sample thickness (pathlength)
• The Absorptivity (e) is a measure of a molecule’s absorbance at a given
wavenumber normalized to correct for concentration and pathlength – but as
shown can be concentration dependent if molecules interact
Peak Widths
Water
Water
Benzene
• Peak Width is Molecule Dependent
• Strong Molecular Interactions = Broad Bands
• Weak Molecular Interactions = Narrow Bands