Download Document

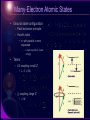
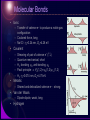
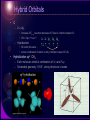
Physical Background
Atomic and Molecular States
• Rudiments of Quantum Theory
– the old quantum theory
– mathematical apparatus
– interpretation
• Atomic States
– hydrogen
– many-electron
• Molecular states
– classification
– chemistry
Rudiments of Quantum
Theory
Photons and Particles
• Electromagnetic field
– The wave equation
– Plane waves, The wave function
Maxwell equations
Space and time change of phase
  2 T  2  k c [rad / s]
k  2 
[rad / m]
• Planck’s hypothesis, dualism
– Particle (E,p)(,k) de Broglie wave
Relativistic relation Ep
E 2 c 2  p 2  m02 c 2
photon : p  E c
Bohr’s Model of the Hydrogen Atom
•
Classical atom
– Unstable: accelerated motion, continuous
radiation
•
Bohr’s rules
– Quantized angular momentum
• Only certain circular orbits allowed
• Discrete set of stationary states
• Discrete spectrum of energy
– Discrete spectrum of radiation
– Coulomb and centrifugal force
– Bohr radius
Mathematical Apparatus
•
Philosophy: Act of observation
– Interaction through which the quantity is
‘observed’
General operator
 
Aˆ  Aˆ  x, 
 x 
– Possible results of observation
– Non-commuting observations
•
Mathematics: operators in Hilbert space
– Eigenvalue equation

x
x
a1 0 
0 a 
2

Operator algebra


x  1 x
x
x
– Commutation relations
 
 x, x   1
Mathematical Apparatus
•
Interpretation postulates
– Possible results of observation  are
eigenvalues an
– Observation  on a system in eigenstate
n certainly leads to an
– The mean value of the observable  on
the ensemble of systems 
•
Physical postulates
– The correspondence principle
• In the limit of ‘large’ system quantum
laws reduce to classical laws
• Relation between classical quantities
with no derivatives holds also for
quantum operators
– The principle of complementarity
• The Heisenberg uncertainty principle
Mean value
a 
*

 ( x) Aˆ  ( x)dx
*

 ( x) ( x)dx
Complementarity principle
perturbati on  xˆ , pˆ   


x
,



 

x 
  i  u p  exp  ipx /  
gen.coordinate, gen.momentum
Xˆ , Pˆ   i
Schrödinger representation
“An experiment on one aspect of a system is supposed to destroy the
possibility of learning about a 'complementary' aspect of the same system”.
xˆ  x; pˆ  i

x
Angular Momentum
•
Space orientation of the orbit
– Magnetic and electric moments
• Internal and external interactions
•
Classical
•
Quantum
– Spherical coordinates
• Boundary condition +2n
L  mrv  mr 2  I
Ek  p 2 2m  1 2 I 2  L2 2 I
The Copenhagen Interpretation
•
radioactive isotope
Probabilistic approach
cyanide capsule
– Probability density
•
Collapse of the wave function
– Schrödinger’s Cat
– Two-Slit Experiment
Indeterminate quantum
states “collapse” to definite
values when they do, not
when a human being catches
them in the act
Atomic States
Hydrogen
•
•
Particle in a central potential
Coulomb potential
[ Hˆ , lˆ 2 ]  [ Hˆ , lˆz ]  0  n,l ,m
SO coupling – internal Zeeman
VB  μB
B
– Electron spin
– Fine structure: relativistic corrections
• Electron-nucleus, Kinetic energy, Spinorbit interaction
– Lamb shift
– Hyperfine structure
0e
l
4me r 3
μ
e
s
me
Hˆ SO   (r )ˆlsˆ
Hydrogen
Many-Electron Atomic States
• Ground state configuration
– Pauli exclusion principle
– Hund’s rules
• e– with parallel s more
separated
– Lower repulsion, lower
energy
• Terms
– LS coupling: small Z
• L, S, J (M)
– j-j coupling: large Z
• J, M
Molecular States
Molecular Bonds
• Ionic
– Transfer of valence e– to produce a noble gas
configuration
– Coulomb force, long
– Na+Cl-: re=0.24 nm, De=4.26 eV
• Covalent
–
–
–
–
–
Shearing of pair of valence e– ()
Quantum mechanical, short
H2: bonding S, anti-bonding A
Pauli principle  A(1,2)=S(1,2)(1,2)
H2: re=0.074 nm, De=4.75 eV
• Metallic
– Shared and delocalized valence e– - strong
• Van der Waals
– Dipole-dipole, weak, long
• Hydrogen
Electronic States
• Born-Oppenheimer Approximation
U
– Separation of electronic and nuclear
motion
U
– Electronic motion – nuclei fixed
internuclear distance r
Electronic States
• Classification
– Total orbital momentum along internuclear
axis in the electric field
• Internal Stark effect
– Total spin along internuclear axis
• magnetic coupling
– Parity of el
• Inversion about a plane through the axis: +/• Inversion through the center of symmetry: g/u
– Homonuclear molecules
Electronic potentials Mg2
Nuclear Motion
•
Rigid rotator
2
ˆ2
J
J
(
J

1
)

Hˆ 
 EJ 
2I
2r 2
•
Harmonic oscillator
Harmonic (Hook)
V(r)
d 2  2
E  V (r ) ; F  kr;

dr 2  2
1
1
V (r )  k (r  re ) 2   cl2 (r  re ) 2 ;
2
2
Ev   cl (v  1 2)
•
Anharmonic oscillator
– Morse potential V (r )  De 1  exp   (r  re )
Morse
re
De
Nuclear Motion
•
Vibrating rotator
– 100 vibrations during a revolution
1
– Averaged rotational constant
Bv   2 
 r v
– Mean value (1/r2)v decreases as v
increases
Bv  Be   e (v  1 2)
– Centrifugal force
•
Coupling of electronic and nuclear
motion
– Hund’s cases
• Coupling between various angular
momentum vectors
– Gyroscopic forces disturb orbital motion of
electrons
– Internal magnetic fields from the rotation of
nuclei couple with the electron spin
– Total angular momentum J
Molecular Orbitals
•
•
LCAO (Linear Combination of Atomic Orbitals), perturbation theory
Homonuclear diatomics
– Correlation diagram; surfaces of probability ||2, ||2
H2
united atoms He
separated atoms H
3d
4d
4p
4s
s
3p
bonding
+
s
antibonding
3s
2pg*
2pg
3p
3s
2p
2su*
2pu
pz
2s
+
pz
2s
1su*`
1s
1s
+
internuclear distance re
Li2 N2
+
+
bonding
+
+
pzg
pz
+
px
+
+
+
+
pzu*
pz
bonding
+
+
px
px
1sg
H2
+
antibonding
2sg
2p
+
sg
s  u*
s
s
*
2pu
+
+
+
+
3d
energy
+
+
+
pxu
antibonding
+
+
px
pxg*
Hybrid Orbitals
•
C
– 2s2pz
• Increase of Esp less than decrease of E due to 4 bonds instead of 2
• CH4: 3sp + 1ss ?
1s 2s 2p 2p 2p
– Hybridization
x
  
y

z

• All bonds the same
• Linear combination of atomic s and p orbitals in case of EsEp
•
Hybridization sp3 CH4
– Each molecular orbital is combination of ¼ s and ¾ p
– Tetrahedral geometry, 109.5°, strong directional  bonds
sp3
Hybrid Orbitals
Hybrid Orbitals
•
–
–
–
–
–
•
H

3
 bonds, ⅓ s and ⅔ p
H
1 p  bond
sp2 approximately 120°
p perpendicular to axis
 out of the axis, more reactive

Hybridization sp2 C2H4
sp2
Hybridization sp C2H2
– 2 hybrids ½ s + ½ p, 
– 2 pure p, 

H C



C



C

H
H
sp2
CH
sp
Hybrid Orbitals
Hybrid Orbitals
•
•
H
Benzene (sp2) C6H6
Valence bonding theory VB
C
– Each C uses 3 sp2 orbitals to form 
bonds with H and next C
– Planar symmetrical hexagon, 120°
– 6 e– in 6 p orbitals perpendicular to 
bonds form 3  bonds, 2 e– in each
– 3 single and 3 double bonds
•
sp2
H
C
H C
C H
C
H
C
1s
H
Shortcomings
p
– Double bonds are not so stable
– C–C 1.54 Ǻ; C=C 1.35 Ǻ
– No isomeric compounds found
•
Resonance model
– Resonance hybrid between structures
(A) and (B)
– 1.5 bonds between C atoms
H
H
H
H
H
H
H (A)
resonance
H
H
H
H
(B) H
Hybrid Orbitals
•
•
Benzene (sp2) C6H6
Molecular orbital theory MO
–  system of delocalized e–
– C bonds 1.40 Ǻ
– Stability: “delocalization energy”
– VSEPR
• Valence Shell Electron Pair Repulsion Theory
• Predicts the shapes of the molecules
VB hybridizes the atomic orbitals
first then overlaps the resulting
hybrid orbitals by using LCAO.
MO overlaps the atomic orbitals
first by using LCAO followed by
VSEPR concepts.