Download L03_Gauss_Law

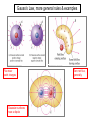
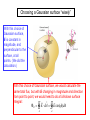
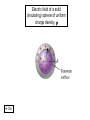
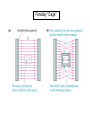
Gauss’s Law
Johann Carl Friedrich Gauss
1777-1855
Mathematics and physics: including number
theory, analysis, differential geometry, geodesy,
electricity, magnetism, astronomy and optics.
y  Be
 cx 2
First, electric flux,  E
“Flux” means “flow”. In this case we are interested in “number of field
lines” passing through a given surface. More precisely, flux is found by
taking the component of the electric field perpendicular to a given
surface, and multiplying by the area of the surface. (Or, equivalently, the
surface area perpendicular to the electric field, times the field, E.)
 E  EA
0o
 
 E  E  A  EA  E ( A cos  )
General expression for a uniform
field passing through a flat surface
90o
E  0
Dimensions of electric flux,  E
 
N 
 E  E   A m2
C 
2
 N  2  N  m  V  2
Dimensions :   m  
   m  V  m

C 
 C  m
 
 
Example: electric flux,  E , for a uniform field through a disk
E = 500 N/C
 Do
The general expression for  E
Unless the surface is flat and the field is uniform over the surface, we
must calculate the flux by integrating the perpendicular (normal)
component of the electric field over the surface.
 
 E   E  dA   E cos( )dA
A
A
But most of the problems
we do will involve simple
surfaces and uniform or
symmetric electric fields!
Gauss’s Law: here it is!
The electric flux through a closed
surface is proportional to the total
charge in the enclosed volume.
E 
Qenclosed
e0
Constant of proportionality = 1/e0
Sometimes the closed surface is that of a
real physical object. Sometimes we create
a closed surface purely for doing the
calculation: a “Gaussian surface”.
Onward, to the examples…
Wunderbar!
The simplest case: a single point charge
We have chosen to surround the
point charge with a spherical
Gaussian surface of radius r
centered on the charge. This
means that the electric field is
perpendicular to the surface,
and is the same magnitude at all
points on the surface. We need
not integrate.
 E  EA 
Qenclosed
e0

q
r
q
e0
Since A = 4p r2
EA  E (4pr ) 
2
q
e0
q
kq
 E
 2
2
4pr e 0 r
This is the electric field for a point charge--found from Coulomb’s Law!!
Gauss’s Law, with point charges in boxes
In these cases, it is easy to find
Qenclosed simply by adding point
charges. But calculating the
total flux through the closed
surface of a box is complicated
since E changes from point to
point. We must integrate
without help from symmetry:
 
 E   E  dA   E cos( )dA
A
A
Then we could apply Gauss’s Law
E 
Qenclosed
e0
Gauss’s Law, more charges in boxes
There are a number of ways
to get zero flux.
Independent of angle
If the charge in the box is
constant, the total flux
through the surface is
constant, even if the surface
is changed.
Gauss’s Law, more general rules & examples
Flux near
point charges
Gaussian surfaces
near a dipole
Zero net flux,
generally.
Choosing a Gaussian surface “wisely”
With this choice of
Gaussian surface,
E is constant in
magnitude, and
perpendicular to the
surface, at all
points. (We did the
calculation.)
With this choice of Gaussian surface, we would calculate the
same total flux, but with E changing in magnitude and direction
from point to point, we would need to do a full-blown surface
 
integral:
 E   E  dA   E cos( )dA
A
A
Electric field of a sheet of charge of
uniform charge density, sigma
s
We choose the surface so
that some faces have zero
flux through them, and some
have perpendicular electric
fields—making the flux
calculation easy.
 Do
Electric field of a charged conducting plate:
two sheets of charge
Slightly different
from the previous
problem!
 Do
Electric fields of a capacitor:
two conducting plates
 Do
Electric field of a line charge of
uniform density, l
We again choose the
surface so that some
faces have zero flux
through them, and some
have perpendicular
electric fields.
 Do
Electric field of a solid
(insulating) sphere of uniform
charge density, r
 Do
Electric field of a solid sphere (above)
Conductors in electrostatic equilibrium:
electric field properties from self-consistency
Starting point: In conductors, charges are free to move, both
inside and on the surface. When they have stopped moving,
the excess charges are in “electrostatic equilibrium”.
I.
In electrostatic equilibrium, there is no field inside a conductor.
Otherwise, the charges inside would continue to move! (F = qE)
II. In electrostatic equilibrium, all excess charges are on the surface
of a conductor. Otherwise, there would be electric fields inside!
III. In electrostatic equilibrium, the electric field outside the
conductor, and near the surface, is perpendicular to the surface.
Otherwise, excess charges would continue to move along the surface!
 Sketch an oddly shaped
conductor being charged,
and then in equilibrium.
Conductors in electrostatic equilibrium:
electric field properties and Gauss’s Law
Gauss’s Law is
consistent with
properties I. and II.
above.
Conductors in electrostatic equilibrium:
electric field properties and Gauss’s Law
s
We can use Gauss’s
Law, together with
property III., to find the
electric field at any point
near the surface of a
conductor, independent
of shape
Conductor examples: using Gauss’s Law
Faraday’s “Pail”, or “Cup”
Faraday “Cage”
We’ll see more of Faraday’s work as we go along.
From Wikipedia:
Michael Faraday, (1791 – 1867) was an English
chemist and physicist who contributed significantly to
the fields of electromagnetism and electrochemistry. He
established that magnetism could affect rays of light
and that there was an underlying relationship between
the two phenomena.
Some historians of science refer to him as the best
experimentalist in the history of science. It was largely
due to his efforts that electricity became viable for use
in technology. The SI unit of capacitance, the farad, is
named after him. Faraday's law of induction states that
a magnetic field changing in time creates a proportional
electromotive force.
When lightning strikes
Nature, discharging its capacitors.
Faraday’s Car (Not really. It
just looks that old.) 1950
Ford sedan. Discuss.
Calculating the surface charge at each point
on the surface of a conductor
We did this calculation
before, when considering
the field at the surface of a
flat conducting plate. The
same equation, E = s/e0 ,
applies here. But s and E
now vary from one point to
the next on the surface.
The Van de Graaf generator
Spherical shell with point charge at center
Find and sketch the field for
(a) a conducting shell, and
(b) an insulating shell
 Do
Comparing electric fields of insulators and conductors:
example of spherical shells charged to +Q and -Q
+Q
R
r
R
-Q
d
1. Consider insulators at distances:
d ~ R, d >> R, and d << R.
2. Consider conductors at distances: d ~ R, d >> R, and d << R.
 Do
Insulating sphere of uniform charge
density, with spherical cavity
 Do
Inverse square law again – with Gaussian surfaces
 Discuss
Gauss’s Law with both sides in integral form
  Qenclosed
1
 E   E  dA 

A
e0
e0
 rdV
V
In this form, it is clear that Gauss’s Law can be used to analyze any
shape of closed surface enclosing any distribution of charge.
In mathematical terms, this equation is a special case of the
“Divergence Theorem”, also known as “Gauss’s Theorem”. The
Divergence Theorem is one of a several integral equations from the
area of “vector calculus”.