* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The Quantum Hall Effects: Discovery, basic theory and open problems
Elementary particle wikipedia , lookup
Identical particles wikipedia , lookup
Hydrogen atom wikipedia , lookup
History of quantum field theory wikipedia , lookup
Particle in a box wikipedia , lookup
Ferromagnetism wikipedia , lookup
Wave–particle duality wikipedia , lookup
Atomic theory wikipedia , lookup
Electron scattering wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Canonical quantization wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
The Quantum Hall Effects:
Discovery, basic theory and open problems
K. Das Gupta
IIT Bombay
Nanoscale Transport 2016, HRI (Feb 24 & 25, 2016)
Topics
The classical Hall voltage
Current flow pattern in a Hall bar (How to solve)
Discovery of the Quantum Hall
The role of mobility
The 2DEG in a MOSFET
Setting up the Quantum Mechanical Hamiltonian (effective masses etc)
Oscillation of the Fermi Level, Landau levels
Group velocity of the eigenstates
Channels from a contact to another
Edge states (why is this quantisation perfect)
The logitudinal resistance oscillation
The Fractional Hall State (Discovery)
Rotationally invariant solutions
Many body states in the first Landau Level
The fake plasma analogy and the Laughlin states
Correlations predicted by the Laughlin wavefunctions
Why does one need to go beyond the Laughlin states
The Classical Hall effect is not entirely trivial
Current flowing through a rectangular block should satisfy:
V=V0
=
0
= σE
= −∇ V
=
0
y
L
∇. j
j
E
∇2 V
x
What are the boundary conditions ?
V ( x , 0)
V ( x , L)
j x (W /2, y)
j x (−W / 2, y)
= 0
= V0
= 0
= 0
solution :
y
V ( x , y) = V 0
L
V=0
The solution is simple becuase the relation between j and E is simple.
What happens when we introduce B?
The boundary conditions DO NOT change in any way.
W
The Classical Hall effect is not entirely trivial (Boltzmann transport)
()
(
σ0
jx
1 −μ B
=
2 2
jy
1+μ B μ B 1
)( )
Ex
Ey
equivalently
() (
Ex
ρ0
=
Ey
−B/nq
Notice ρxx = 0
⇒
B/nq
ρ0
)( )
jx
jy
typical value ~ 10-2 -10-3
But high mobility
will lead to large angle
The angle between E and j
B/ nq
tan δ = ρ
= μB
0
How does the current flow pattern look?
Remember σ is now a 2×2 matrix
σ xx = 0
Can be solved exactly with a conformal map
connecting the two shapes.
E y (x , y )+i E x ( x , y) = exp [ f (Z )]
f (Z )
=
∑
n odd
y
x
4 δ sinh (n π Z / L)
n π cosh (n π W / L)
How do these solutions look?
Z =x+iy
Rendell & Girvin, PRB 23, 6610(1981)
The Classical Hall effect is not entirely trivial : [left] d=0 and [right]d=0.95p/2
Current density vector j
The Classical Hall effect is not entirely trivial [top] d=0 and [bottom]d=0.95p/2
d=0
d=0.95p/2
Vectors denote the current flow. For hall angle close to 90, current will flow along
equipotentials....each long edge becomes an equipotential!
The Classical Hall effect : Do we actually see d=0.95p/2 type states ?
Mobility and not conductivity
fixes the Hall angle
For metals (''pure'' Cu, Ag at low temp) :
n ~ 1029 m-3 r=10-9 Wm : so m ~ 0.1 m2/Vs
Si MOSFET : n~1015 m-2 m ~ 1-10 m2/Vs
It is only in semiconductors
mB >> 1 is possible
In metals Hall voltage is useful for measuring
carrier density etc...
''Anomalous Hall“ in ferromagnets
But large hall angle is not possible
Pfieffer & West, Physica E, 20, p57-64 (2003)
The Classical Hall effect : What did we find for the very high field case ?
Thus two voltage probes placed at two points on the (long) side may measure no voltage drop.
The current density at the corner is very high.
All the current emanates from the edge of the ohmic contacts (the points of mathematical
singularity of the series solution) and carries with it the potential of the contact.
We did not require much "quantum" physics to establish the important fact that almost dissipationless channels can arise in a strong magnetic field, irrespective of the amount of disorder
initially present. The zero field resistance dropped out of our consideration.
The two-probe resistance measured between the ohmic-contacts and the Hall voltage
measured between the opposite sides of the Hall bar will be the same.
The Hall voltage measurement does not require that the Hall voltage probes be exactly
opposite to each other.
Gives an idea why ohmic contact often fails in high magnetic fields.
What did the experiments show?
PRL 45, 494 (1980)
The Hall voltage becomes flat at specific values:
Samples from different labs/factories differing in microscopic details give the
flat plateau at the same resistance value.
These data were from Si MOSFETS, today GaAs-AlGaAs heterostructure is
more commonly
The exactness of the quantisations
Material independent constants are quite rare in Condensed matter
The resistance of the first quantum Hall plateau : 25.812807....kohms
(Any 2D electron gas satisfying some basic criteria)
The Josephson frequency 483.5979 Mhz/microvolt
(any superconducting weak link, irrespective of the material used)
Each of them correct to at least 8 significant figures...
Electrons in a band and the effective Schrödinger equation
A slowly varying potential is applied in addition to the lattice potential...
[
]
p2
H =
+V l +V slow
2m 0
Ho
Free electron mass
NOT effective mass
Vl is the fast varying
lattice potential
Bloch
d3k
i k .r
Ψ= ∫
c
(k
)
u
(k
)e
3
FBZ (2 π)
d3k
i k .r
HΨ= ∫
c
(k
)
H
[
u
(k
)e
]+V slow Ψ=E Ψ
0
3
FBZ (2 π)
3
d k
i k.r
c(
k
)
E
(k
)
u(k
)
e
]+V slow Ψ= E Ψ
[
∫ (2 π)3
FBZ
E ( k ) is the band dispersion
Approximation can be done after the KE operator has acted, not before..
c (k )mostly peaked around k =0 and u(k ) does not change wildy with k
Call this F(r)
d3k
d3k
d3k
ik .r
i k. r
i k .r
u0 ∫
E
(k
)c
(k
)e
+
V
u
c
(k
)
e
=
E
u
c
(k
)e
∫
∫
slow 0
0
3
3
3
FBZ (2 π)
FBZ (2 π)
FBZ (2 π)
The only r dependence is in ei k . r : so E (k ) e i k .r =E (−i ∇ ) e i k .r
Electrons in a band and the effective Schrödinger equation
ℏ2 k 2
simplest parabolic band : E (k )=
: So
2m eff
[
2
]
p
+V slow F (r )=EF (r)
2m eff
All effects of the complicated latttice
potential somehow gets parametrized into
a single effective mass.
The equation retains its structure!
If there is a magnetic field, then
[
A remarkable simplification...
]
1
2
( p−q A) +qV slow ψ = E ψ
2m eff
This is the Schrodinger equation we usually
deal with.
Similar treatment can be done for
graphene, which satisfies a different
equation.
Sheet of electrons in a magnetic field : Landau levels
Take A = B(0, x , 0)
1
2
2
Then H =
p
+(
p
+eBx
)
[
]
y
2m x
ψ( x , y) = eiky f k ( x)
[
]
px2
1
+
( ℏ k +eBx )2 f k ( x ) = Ef k ( x )
2m 2m
eB
ω =
m
harmonic oscillator
ℏk
x0 =
eB
2
p x mω 2
+
( x+ x 0)2 f k ( x) = Ef k (x)
2m
2
1
ℏk
E n = ν+ ℏ ω
x0 =
= kl 2
eB
2
[
]
( )
l2 =
l
≈
ℏ
eB
257 A
√B
A = B(0,x,0)
Different choice of A will help if
rotational symmetry is useful.
A=B(-y/2, x/2,0)
Classical arguments gives same
Cyclotron freq (independent of h)
Cannot give cyclotron radius, which
depends on h
Degeneracy and other basic properties of the Landau levels
The eigenvalues are independent of k, leading to massive degeneracy.
The center of the ''oscillator'' must lie within the LxW sample
W /l
2
L
dk
∫
2π 0
LW eB
=
2π ℏ
eB
= Area ×
h
N =
Periodic boundary
Condition, think of the
sheet as rolled up
in a certain direction
14
−2
≃10 m
a very large degeneracy
The states are actually strongly overlapping!
L=1 mm sample
B=1 Tesla
spatial width of nth harmonic oscillator state
≈
spatial separation between two states
2π 2
=
l
L
δ x0
√n l
= 2πl
()
l
L
Calculate the
separation & width
L≫l
Many body
effects??
Where is the Fermi level?
Consider N spinless particles per unit area ( B=0)
m
D(E ) =
2
2πℏ
m
N =
E f (0)
2
2πℏ
Index of the highest occupied level when B≠0 ?
N
νmax =
eB/h
1
E f ( B) = ν max + ℏ ω
2
ℏ eB/m
E f (0)
1
1
x=
=
+
x
E f (0)
E f ( B)
2
x
[ ]
( )
( [ ])
A voltmeter will measure
difference in
electrochemical potential
Pudalov et al, JETP 62, 1079 (1985)
~20kB / Tesla in GaAs
Oscillation of the Fermi level with changing magnetic field
What happened to cyclotron motion? Where are these states physically located?
Classical picture : charged particles have ''orbits'' in a magnetic field.
But now.....calculate the current
e
〈 J y 〉 = − 〈 ψ k | p+e A | ψk 〉
m
( x+kl )
−
e ωc
2
=−
dx e l ( x+kl )
∫
√π m
2 2
2
A state like e i k .r is everywhere
2
But not
1 iky
e H n (x+x 0 )e
√L
(x+ x 0)
−
2
2l
Will give zero, but the change
of the sign on two sides of the
gaussian is the ''remnant'' of
classical circulation.
This is same as the
Band bending approximation
In a solid, some fundamental
Questions can be raised,
But the approximation works!!
ℏk
: so value of k decides that
eB
In presence of a potential U slowly varying on a scale of l
E (x 0 ) = (ν+1/2)ℏ ω+U ( x 0)
E (k ) = (ν+1/ 2)ℏ ω+U (kl 2 )
x 0=
States near the edge and states in the bulk have different group velocities
∂E
<0
∂k
∂E
=0
∂k
Increasing x (or k)
The quantum mechanical view:
A state cannot carry current, if......
vg=0
Fermi level doesn't have a finite D(E)
∂E
>0
∂k
1 ∂E
vg =
̂y
ℏ ∂ky
The semiclassical
complete closed and
incomplete skipping
orbits
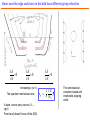
Conduction from one lead to another
Ohmic contact=
Black body!
Current starting from one lead must
either be backscattered or end up in
the other lead.
Those which start from a lead
carry with them the
electrochemical potential of that
lead...till they equilibrate with
some other lead.
Conduction from one lead to another
∞
I L → R = e ∫ dE D(E ) f ( E ,μ L )v g ( E )T (E)
−∞
∞
I R → L = e ∫ dE D(E ) f ( E ,μ R ) v g ( E )T (E )
−∞
∞
I = e ∫ dE D ( E) [ f ( E ,μ L )− f (E ,μ R ) ] v g T (E )
−∞
μR
I ≈e ∫ dE D( E)v g (E )T ( E)
μL
1 1
D( E ) = π
dE /dk
1 dE
vg =
ℏ dk
In 1D the two
factors cancel
μR
I ≈e∫ dE D( E ) v g ( E )T ( E )
μL
2 e2
=
(V R−V L )T ( E )
h
At the end: the current does not
depend on how many carriers are
there in the channel!
What is the value of T(E)?
What should be the value of T(E) ?
T ( E )≠1
T ( E )=1
lead inserts some excess carriers δ n = ND( E) e δ V
I = ( ev g ) ND ( E)e δV
2
RH
e
= N δV
h
δV
h
=
=
2
I
Ne
1
1
D(E ) = π
dE /dk
1 dE
vg =
ℏ dk
Key features of the Quantum Hall state
Data: KDG, (Semiconductor Phy group, Cavendish Lab)
The oscillation of the longitudinal resistance
Basic question: How much is the density of states near the Fermi level?
If Fermi level does not lie in a continuum then a charge cannot accept a small
amount of energy and accelerate.
Of course it can jump across a gap if energy is sufficient (1 kelvin = 2.08 x 10 10 Hz)
The Fractional Quantum Hall effect (1982)
The Fractional Hall State (Discovery)
Rotationally invariant solutions
Many body states in the first Landau Level
The fake plasma analogy and the Laughlin states
Correlations predicted by the Laughlin wavefunctions
Why does one need to go beyond the Laughlin states
The even denominator states and the open questions
Discovery of the Fractional Quantum Hall effect (1982)
Looking for Wigner crystal phases
Expectation: at high fields electrons may
localise in a lattice
Prediction from 1930s by Wigner
The FQHE state occurs in sample with
higher mobility: here
n~1011 cm-2
m~105 cm²/Vs
Tsui, Stormer, Gossard PRL 48,1559 (1982)
FQHE: Initially the fractions all seen to have odd denominators...but
Why was this striking?
The proposed wavefunction for the
FQHE states (Laughlin) can work for
odd denominators only.
Also fractions like ½ , ¼ are not seen in
the first Landau Level
Willett et al PRL 59,1776 (1987)
FQHE: Closer look at the 5/2 even denominator state
J C Dean: PhD Thesis (McGill Univ, 2008)
Notice the extremely low electron temperature
necessary to see the state clearly
FQHE: The skyline of states known today.....odd, even
n~1011 cm-2
m~107 cm²/Vs
Notice that
higher mobility
leads to
discovery of
more and more
fractional states
Pan et al PRL 88,176802 (2002)
So, where do we start …..
The states in the first Landau level are strongly overlapping:
High magnetic field suppresses screening
''Quenches'' kinetic energy (meaning E ~ k, k2 no longer holds)
All these taken together means......
The repulsive Coulomb interaction will play an important role
We need to write a manybody wavefunction for electrons in LL=1
We didn't need to do this for IQHE (non-interacting picture was sufficient)
Also we are dealing with a no-small-parameter, non-perturbative problem!
Complex number trick (useful for 2D electrostatics) turns out to be very
useful...
Rotationally symmetric states (angular momentum eigenfn) for Landau levels …..
With A=B(0, x , 0) we had
2
1 iky
ϕn ( x , y) =
e H n ( x+x 0 )e
L
√
(x+ x 0)
−
2
2l
The fixed angular momentum
States are localised in both x & y
Unlike the cartesian solution
With A=B(− y /2, x / 2,0) we will get
ϕ0, m (x , y) =
1
√2 π l
2
m
m
2 m!
−
z e
| z|
4
2
x+iy
l
iky
instead of e
i mθ
these have e
here z =
The higher levels are generally derived by recurrence
(
*
n
)
z
ϕn ,m = 2 ∂ − 2 ϕ0,m
∂ z 2l
..... not needed if we are in LL1
2
−
| z|
4
Any polynomial f (z )× e
Will also be a valid wavefn in LL1
But not with a fixed L z
So we have many states with in LL1 with different angular momenta.
How do we put many particles in them?
Writing the wavefunction for many electrons together …..
Question:
We have n states (orbitals) to put n
electrons. How to do it ensuring the
indishtiguishability of the particles?
Quantum statistics
There should be no way to distinguish
particle 1 from particle 2,3,4 etc.
Exchanging any two particles...
FERMIONS:
…..results in the same wavefunction
with a negative sign.
BOSONS:
…...results in the same wavefunction
Many body state with all particles in LL1 …..
Let z i denote the co-ordinate of the i th particle
∣
( z 1 )0
( z 2)0
...... (z N )0
1
1
1
( z 2)
Ψ[ z ] = ( z 1 )
⋮
⋮
( z 1 )N −1 ( z 2) N −1
1
−
4
N
Ψ[ z ] = −∏ (z i−z j )e
∣
Determinant form automatically
satisfies the antisymmetry.
There are no ''wasted zeros''
1
−
4
...... (z N )
× e
....... ⋮
...... (z N )N −1
N
∑ | zi |2
i
The Vandermonde form of the
matrix...easy to see what the
roots are
But there are no free
parameters left for us to tweak!
N
∑ | z i |2
i
i< j
Question: Is there any kind of structure in the wavefunction we have written?
N (N −1)
2
2
2
g ( z) =
d
z
…
d
z
|
Ψ(0,
z
,
z
,…
,
z
)|
∫
∫
3
N
2
N
n2 Z
Z = 〈 Ψ|Ψ〉
1 2
− |z|
2
g ( z) = 1−e
can be exactly calculated!
Inverted gaussian.
No peaks or structure
Try to get a feel of the terms in the wavefunction: analogy of a fake 2D jellium !
Jellium
Uniform structureless background positive charge
The lattice is abstracted away
Free electrons with Coulomb interaction move around
Background and average electron charge density cancel exactly
Useful theoretical construct
Partition function of a fake 2D jellium !
N
1
− ∑ | z i |2
4 i
N
Ψ [z ] = −∏ (z i−z j )e
i< j
Z ≡∫ d 2 z 1 …∫ d 2 z N | Ψ [ z ]|2
2
−βU
Imagine | Ψ [ z ]| as e
2
β=
and
m
U ≡m2 ∑ ( −ln | z i−z j | ) +
i< j
where
m
2
|
z
|
∑
4 k k
charge neutrality will require :nm+ρB =0
ℏ
2
since l =
eB
m can be imagined as the filling fraction
!! hypothetical 2D electrostatics (in cgs units)!!
∮ E . dl = 2π Q
Coulomb interaction is then given by
Q r̂
E(r ) =
r
r
V (r ) = Q −ln
r0
since r 0 is arbitrary, free to set r 0=l
consider each particle to have charge : m units
interaction energy can be summed pairwise:
( )
m 2 ∑ ln ( | z i−z j | )
i< j
2
For a point charge ∇ V = −2 π δ(r )
2
1
2 |z |
so ∇
= 2
4
l
set the uniform background to be ρ B=−
...second term follows
1
2
2πl
The Laughlin wavefunction............it is an educated guess!
N
N
−
Ψ1 /3 [ z ] = −∏ ( z i−z j) e
3
1
2
|
z
|
∑ i
4 i
i< j
Antisymmtery is preserved. What two point correlations does it predict?
Is there any structure now?
Solid lines : Monte-Carlo data
Dots : Laughlin wavefn
For m > 7 this form isn't the best
S. Girvin, Les Houches lecture notes 1998
arXiv: 9907002
The Laughlin wavefunction : How do we show there is an excitation gap?
Excitation above a many body state will be some collective excitation
Like Spin wave in Ferromagnet is diferent from flipping a single spin.
1
Δ (k ) = 〈 Ψ (k )| H−E 0 | Ψ( k )〉 .
S (k)
S ( k )=N δ k , 0+1+n ∫ d r e
3
ik .r
[ g ( r )−1 ]
But in this case we need to ensure that the excited
state is still part of LL1.
So, need to ''project'' the density fluctuation on the
LL1 and then calculate the quantitites
4
Turns out both quantites vary as ~ k
Hence the gap, since the ratio stays finite
Relating the static
structure factor to
excitation spectrum.
Feynman & Bijl
Abrikosov & Gorkov
ℏ2 k 2
2M
if the sum was
not restricted
to LL1
Is the FQHE after all IQHE (of some composite object) in disguise?
This question leads to the
COMPOSITE FERMION
picture (Jainendra Jain)
PRL 63, 199 (1989).
PRB 41, 7653 (1990).
Predicts FQHE at fractions:
p
2mp±1
m , p : small integers
ν =
But still it will have odd
denominator fractions only
J C Dean: PhD Thesis (McGill Univ, 2008)
References:
S M Girvin, Les Houches Summer school Lecture notes (1998)
J H Davies, Physics of Low dimensional Semiconductors
J K Jain, Composite Fermions (Cambridge University Press)
K. von Klitzing, M. Pepper, G. Dorda, PRL 45, 494 (1980)
D. Tsui, H. Stormer, Gossard PRL 48,1559 (1982)