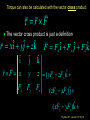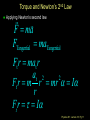* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Ppt
Tensor operator wikipedia , lookup
Angular momentum operator wikipedia , lookup
Photon polarization wikipedia , lookup
Rolling resistance wikipedia , lookup
Inertial frame of reference wikipedia , lookup
Rotating locomotion in living systems wikipedia , lookup
Coriolis force wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Center of mass wikipedia , lookup
Jerk (physics) wikipedia , lookup
Classical mechanics wikipedia , lookup
Renormalization group wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Equations of motion wikipedia , lookup
Centrifugal force wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Fictitious force wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Hunting oscillation wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
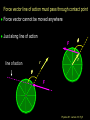
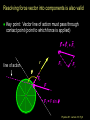
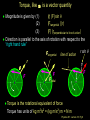
Lecture 18 Goals: • Define and analyze torque • Introduce the cross product • Relate rotational dynamics to torque • Discuss work and work energy theorem with respect to rotational motion • Specify rolling motion (center of mass velocity to angular velocity • So what causes rotation? Physics 201: Lecture 18, Pg 1 So what forces make things rotate? Which of these scenarios will cause the bar to spin? Fixed rotation axis. A F F B F C F F D F F F E Physics 201: Lecture 18, Pg 2 Net external torques cause objects to spin An external force (or forces) properly placed induced changes in the angular velocity. This action is defined to be a “torque” A force vector or a component of a force vector whose “line of action” passes through the axis of rotation provides no torque A force vector or the component of a force vector whose “line of action” does NOT pass through the axis of rotation provides torque The exact position where the force is applied matters. Always make sure the force vector’s line of action contacts the point at which the force is applied. Physics 201: Lecture 18, Pg 3 Net external torques cause objects to spin Torque increases proportionately with increasing force Only components perpendicular to r vector yields torque Torque increases proportionately with increasing distance from the axis of rotation. | r || F | sin This is the magnitude of the torque is the angle between the radius and F r the force vector Use Right Hand Rule for sign Physics 201: Lecture 18, Pg 4 Force vector line of action must pass through contact point Force vector cannot be moved anywhere Just along line of action F r r line of action F Physics 201: Lecture 18, Pg 5 Resolving force vector into components is also valid Key point: Vector line of action must pass through contact point (point to which force is applied) F = Fr + Ft line of action r Ft Fr Fr F F t = F sin Physics 201: Lecture 18, Pg 6 Exercise Torque In which of the cases shown below is the torque provided by the applied force about the rotation axis biggest? In both cases the magnitude and direction of the applied force is the same. Remember torque requires F, r and sin or the tangential force component times perpendicular distance L F A. B. C. Case 1 Case 2 Same F L axis case 1 case 2 Physics 201: Lecture 18, Pg 7 Torque is constant along the line of action Even though case 2 has a much larger radius vector the torque remains constant. Case 1 : = L F Case 2 : = r F sin = F r sin Notice that the sin = sin (p-) = - cos p sin = sin Case 2 : = r F sin = F r sin = F r sin (p-) = F L Here = 135° and |r| = 2½ L so r sin = 2-1/2 (2½ L ) = L p- L F F L p- axis case 1 case 2 Physics 201: Lecture 18, Pg 8 Torque, like w, is a vector quantity Magnitude is given by (1) |r| |F| sin (2) |Ftangential | |r| (3) |F| |rperpendicular to line of action | Direction is parallel to the axis of rotation with respect to the “right hand rule” r sin F tangential line of action r F F F Fradial Torque is the rotational equivalent of force Torque has units of kg m2/s2 = (kg m/s2) m = N m Physics 201: Lecture 18, Pg 9 Torque can also be calculated with the vector cross product r F The vector cross product is just a definition r xî yˆj zk̂ î r F x Fx ĵ y Fy F Fx î Fy ˆj Fz k̂ k̂ z ( yFz - zFy )î Fz ( zFx - xFz ) ĵ ( xFy - yFx )k̂ Physics 201: Lecture 18, Pg 10 Torque and Newton’s 2nd Law F ma FTangential maTangential Ft r mat r at 2 2 Ft r m r mr I r Ft r I Applying Newton’s second law Physics 201: Lecture 18, Pg 11 Example: Wheel And Rope A solid 16.0 kg wheel with radius r = 0.50 m rotates freely about a fixed axle. There is a rope wound around the wheel. Starting from rest, the rope is pulled such that it has a constant tangential force of F = 8 N. How many revolutions has the wheel made after 10 seconds? F r Physics 201: Lecture 18, Pg 12 Example: Wheel And Rope m = 16.0 kg radius r = 0.50 m F = 8 N for 10 seconds Constant F Constant constant Isolid disk = ½ mr2 = 2 kg m2 I = = r F = 4 Nm/ 2 kg m2 = 2 rad/s2 0 w0 Dt + ½ Dt2 - 0 w0 Dt + ½ Dt2 Rev = ( - 0) / 2p ( 0 + ½ Dt2 )/ 2p Rev = (0.5 x 2 x 100) / 6.28 = 16 F r Physics 201: Lecture 18, Pg 13 Work Consider the work done by a force F acting on an object constrained to move around a fixed axis. For an angular displacement d then ds = r d F dW = FTangential dr = Ft ds dW = (Ft r) d axis of R rotation d dr =Rd dW = d (and with a constant torque) We can integrate this to find: W = (f - i) Physics 201: Lecture 18, Pg 14 Rotation & Kinetic Energy... The kinetic energy of a rotating system looks similar to that of a point particle: Point Particle K mv 1 2 Rotating System 2 v is “linear” velocity m is the mass. K Iw 1 2 2 w is angular velocity I is the moment of inertia about the rotation axis. I mi ri 2 i Physics 201: Lecture 18, Pg 15 Work & Kinetic Energy: Recall the Work Kinetic-Energy Theorem: DK = WNET or WEXT This is true in general, and hence applies to rotational motion as well as linear motion. So for an object that rotates about a fixed axis: DK I (w - w ) WNET 1 2 2 f 2 i Physics 201: Lecture 18, Pg 16 Example: Wheel And Rope A solid 16 kg wheel with radius r = 0.50 m rotates freely about a fixed axle. There is a rope wound around the wheel. Starting from rest, the rope is pulled such that it has a constant tangential force of F = 8 N. What is the angular velocity after 16 revolutions ? F r Physics 201: Lecture 18, Pg 17 Example: Wheel And Rope Mass 16 kg radius r = 0.50 m Isolid disk=½mr2= 2 kg m2 Constant tangential force of F = 8 N. Angular velocity after you pull for 32p rad? W = F (xf - xi) = r F D =0.5 x 8.0 x 32p J = 402 J DK = (Kf - Ki) = Kf = ½ I w2 = 402 J w = 20 rad/s F r Physics 201: Lecture 18, Pg 18 Exercise Work & Energy Strings are wrapped around the circumference of two solid disks and pulled with identical forces for the same linear distance. Disk 1, on the left, has a bigger radius, but both have the same mass. Both disks rotate freely around axes though their centers, and start at rest. Which disk has the biggest angular velocity after the pull? w w1 2 W = F d = ½ I w2 Smaller I bigger w (A) Disk 1 start (B) Disk 2 (C) Same finish F F d Physics 201: Lecture 18, Pg 19 Home Example: Rotating Rod A uniform rod of length L=0.5 m and mass m=1 kg is free to rotate on a frictionless pin passing through one end as in the Figure. The rod is released from rest in the horizontal position. What is (A) its angular speed when it reaches the lowest point ? (B) its initial angular acceleration ? (C) initial linear acceleration of its free end ? L m Physics 201: Lecture 18, Pg 20 Example: Rotating Rod A uniform rod of length L=0.5 m and mass m=1 kg is free to rotate on a frictionless hinge passing through one end as shown. The rod is released from rest in the horizontal position. What is (B) its initial angular acceleration ? 1. For forces you need to locate the Center of Mass CM is at L/2 ( halfway ) and put in the Force on a FBD 2. The hinge changes everything! L m mg S F = 0 occurs only at the hinge but z = I z = r F sin 90° at the center of mass and (ICM + m(L/2)2) z = (L/2) mg and solve for z Physics 201: Lecture 18, Pg 21 Example: Rotating Rod A uniform rod of length L=0.5 m and mass m=1 kg is free to rotate on a frictionless hinge passing through one end as shown. The rod is released from rest in the horizontal position. What is (C) initial linear acceleration of its free end ? 1. For forces you need to locate the Center of Mass CM is at L/2 ( halfway ) and put in the Force on a FBD 2. The hinge changes everything! L m a=L mg Physics 201: Lecture 18, Pg 22 Example: Rotating Rod A uniform rod of length L=0.5 m and mass m=1 kg is free to rotate on a frictionless hinge passing through one end as shown. The rod is released from rest in the horizontal position. What is (A) its angular speed when it reaches the lowest point ? 1. For forces you need to locate the Center of Mass CM is at L/2 ( halfway ) and use the Work-Energy Theorem 2. The hinge changes everything! L m mg L/2 W = mgh = ½ I w2 W = mgL/2 = ½ (ICM + m (L/2)2) w2 and solve for w mg Physics 201: Lecture 18, Pg 23 Connection with CM motion If an object of mass M is moving linearly at velocity VCM without rotating then its kinetic energy is 2 K T 12 MVCM If an object of moment of inertia ICM is rotating in place about its center of mass at angular velocity w then its kinetic energy is K R I CMw 1 2 2 What if the object is both moving linearly and rotating? K I CMw MV 1 2 2 1 2 2 CM Physics 201: Lecture 18, Pg 24 Rolling Motion Now consider a cylinder rolling at a constant speed. VCM CM The cylinder is rotating about CM and its CM is moving at constant speed (VCM). Thus its total kinetic energy is given by : K TOT I CMw MV 1 2 2 1 2 2 CM Physics 201: Lecture 18, Pg 26 Rolling Motion Again consider a cylinder rolling at a constant speed. 2VCM VCM CM Physics 201: Lecture 18, Pg 27 Rolling Motion Now consider a cylinder rolling at a constant speed. VCM CM The cylinder is rotating about CM and its CM is moving at constant speed (VCM). Thus its total kinetic energy is given by : K TOT I CMw MV 1 2 2 1 2 2 CM Physics 201: Lecture 18, Pg 28 Motion Again consider a cylinder rolling at a constant speed. Rotation only vt = wR CM Both with |vt| = |vCM | 2VCM VCM CM Sliding only VCM CM Physics 201: Lecture 18, Pg 29 For Tuesday Read though 11.3 Physics 201: Lecture 18, Pg 30