* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download SEM details (chapter 6) - Bill Shipley recherche
Survey
Document related concepts
Transcript
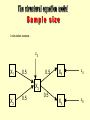
Measurement model 1 Measurement model 2 Structural model Ambient air temperature Thermometer reading Metabolic rate of animal Thermocouple reading Rate of CO2 increase in chamber Rate of O2 decrease in chamber Heat production of animal L X1 Z=X+Y X=3 What is the value of z? L=N(0,) =N(0,) X1 = aL + i.e. 3 free parameters BUT... Z = 3 if Y = 0 Z=6 if Y = 3 and so on for an infinite series of possibilities The equation is underidentified Only 1 element in the covariance matrix (S11) The system is underidentified It is impossible to find single values for the three free parameters given only S11 L X1 1 Fixing the scale of a latent variable L X2 2 L=N(0, ) 1=N(0,) 2=N(0,) X1=a1L+ 1 X2=a2L+ 2 5 free parameters 3 observed values (S11, S12, S22) X1 1 X2 X3 2 3 L=N(0, ) 1=N(0,) 2=N(0,) 3=N(0,) X1=a1L+ 1 X2=a2L+ 2 X3=a3L+ 3 7 free parameters 6 observed values (S11, S12, S13, S22, S23, S33) 1. Chose an observed variable with the same scale and fix the path from the latent to the variable to 1 (therefore 1 less free parameter to estimate). 2. Fix the variance of the latent to a constant (eg. 1) - this fixes its scale to SD units. A B C L L L * * * * * x1 x2 x1 x2 * * * * D x1 * * x2 * x3 * E * F * L L * x1 * * x2 * * * * x3 * x1 * * * x2 x3 x4 * * * * * L1 * L2 * * * x4 * x1 x2 x3 x4 * * * * Model identification becomes quite complicated as the number of latent variables increases. One should carefully develop the measurement models - preferably based on good biological knowledge and a step-by-step process, before trying to evaluate a complicated structural model. What is the nature of the latent variable that I want to model? What would be good indirect measures of this - variables that are not also being caused by other latents that will also be in my model? Keep it as simple as possible! Problem: the probabilities calculated using maximum likelihood methods are only asymptotically unbiased. What does this mean? The calculated probabilities are only exact as sample size reaches infinity!!! In practice, the minimum sample size needed for good probability estimates depends on the ratio of observations to free parameters that have to be estimated. If the data are normally distributed, then 5 times as many observations as free parameters is fine... As the data become increasingly non-normal, the minimum sample size must increase accordingly. If the sample size is not large enough, then the estimated probabilities will usually be smaller than they should be - so you reject models more often than you should. The d-sep test does not have this defect and so small sample sizes are okay. A simulation example... 3 X1 0.5 0.5 X4 4 X5 5 X3 X2 0.5 0.5 100 sample size of 100 0 0 20 20 40 40 60 60 80 80 100 sample size of 10 10 20 30 MLX2 40 10 20 MLX2 30 40 negative skew Problems for estimating means (ANOVA etc) 0.0 0.0 density 0.5 1.0 1.5 density 0.5 1.0 1.5 2.0 2.0 positive skew 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 t-distribution 0.6 0.8 1.0 negative kurtosis normal distribution normal Problems for estimating variances (SEM) 0 density 1 2 3 density 0.0 0.1 0.2 0.3 0.4 0.5 positive kurtosis 0.4 -3 -2 -1 0 1 2 3 0.0 0.2 0.4 0.6 0.8 1.0 Hypothesis: I think that these two variables are independent, and therefore the correlation coefficient must be zero... Ideal case: if the hypothesis is true then my statistical test will never report a low probability value (i.e. below the significance level - say p=0.05) Hypothesis never rejected. if the hypothesis is false then my statistical test will always report a low probability value (i.e. below the significance level) Hypothesis always rejected. 100 % times that the hypothesis is rejected. 0 0 0.1 0.2 0.3 Correlation coefficient 1.0 100 80 60 Sample size N=100 20 40 N=50 N=10 Rejection rate if =0 0 Number of times Ho rejected out of 100 N=500 0.0 0.1 0.2 0.3 True correlation between X and Y () 0.4 0.5 Null hypothesis in testing a structural equation model: The data were generated by the structural equations given in my model - there are no causal relationships in my model that are wrong - there are no causal relationships that are missing in my model - the relationships between the variables are exactly linear - the data are normally distributed or else there are lots of them... As sample size increases, statistical power increases. Therefore, even very small errors in the above assumptions will cause the model to be rejected.