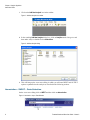
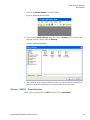
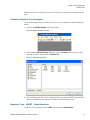
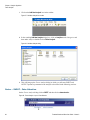
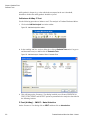
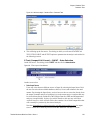
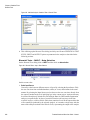
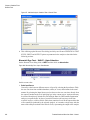
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Teradata Warehouse Miner User Guide
Survey
Document related concepts
Transcript
Teradata Warehouse Miner User Guide - Volume 3 Analytic Functions Release 5.3.4 B035-2302-093A September 2013 The product or products described in this book are licensed products of Teradata Corporation or its affiliates. Teradata, BYNET, DBC/1012, DecisionCast, DecisionFlow, DecisionPoint, Eye logo design, InfoWise, Meta Warehouse, MyCommerce, SeeChain, SeeCommerce, SeeRisk, Teradata Warehouse Miner, Teradata Source Experts, WebAnalyst, and You’ve Never Seen Your Business Like This Before are trademarks or registered trademarks of Teradata Corporation or its affiliates. Adaptec and SCSISelect are trademarks or registered trademarks of Adaptec, Inc. AMD Opteron and Opteron are trademarks of Advanced Micro Devices, Inc. BakBone and NetVault are trademarks or registered trademarks of BakBone Software, Inc. EMC, PowerPath, SRDF, and Symmetrix are registered trademarks of EMC Corporation. GoldenGate is a trademark of GoldenGate Software, Inc. Hewlett-Packard and HP are registered trademarks of Hewlett-Packard Company. Intel, Pentium, and XEON are registered trademarks of Intel Corporation. IBM, CICS, DB2, MVS, RACF, Tivoli, and VM are registered trademarks of International Business Machines Corporation. Linux is a registered trademark of Linus Torvalds. LSI and Engenio are registered trademarks of LSI Corporation. Microsoft, Active Directory, Windows, Windows NT, Windows Server, Windows Vista, Visual Studio and Excel are either registered trademarks or trademarks of Microsoft Corporation in the United States or other countries. Novell and SUSE are registered trademarks of Novell, Inc., in the United States and other countries. QLogic and SANbox trademarks or registered trademarks of QLogic Corporation. SAS, SAS/C and Enterprise Miner are trademarks or registered trademarks of SAS Institute Inc. SPSS is a registered trademark of SPSS Inc. STATISTICA and StatSoft are trademarks or registered trademarks of StatSoft, Inc. SPARC is a registered trademarks of SPARC International, Inc. Sun Microsystems, Solaris, Sun, and Sun Java are trademarks or registered trademarks of Sun Microsystems, Inc., in the United States and other countries. Symantec, NetBackup, and VERITAS are trademarks or registered trademarks of Symantec Corporation or its affiliates in the United States and other countries. Unicode is a collective membership mark and a service mark of Unicode, Inc. UNIX is a registered trademark of The Open Group in the United States and other countries. Other product and company names mentioned herein may be the trademarks of their respective owners. THE INFORMATION CONTAINED IN THIS DOCUMENT IS PROVIDED ON AN “AS-IS” BASIS, WITHOUT WARRANTY OF ANY KIND, EITHER EXPRESS OR IMPLIED, INCLUDING THE IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE, OR NON-INFRINGEMENT. SOME JURISDICTIONS DO NOT ALLOW THE EXCLUSION OF IMPLIED WARRANTIES, SO THE ABOVE EXCLUSION MAY NOT APPLY TO YOU. IN NO EVENT WILL TERADATA CORPORATION BE LIABLE FOR ANY INDIRECT, DIRECT, SPECIAL, INCIDENTAL, OR CONSEQUENTIAL DAMAGES, INCLUDING LOST PROFITS OR LOST SAVINGS, EVEN IF EXPRESSLY ADVISED OF THE POSSIBILITY OF SUCH DAMAGES. The information contained in this document may contain references or cross-references to features, functions, products, or services that are not announced or available in your country. Such references do not imply that Teradata Corporation intends to announce such features, functions, products, or services in your country. Please consult your local Teradata Corporation representative for those features, functions, products, or services available in your country. Information contained in this document may contain technical inaccuracies or typographical errors. Information may be changed or updated without notice. Teradata Corporation may also make improvements or changes in the products or services described in this information at any time without notice. To maintain the quality of our products and services, we would like your comments on the accuracy, clarity, organization, and value of this document. Please e-mail: [email protected] Any comments or materials (collectively referred to as “Feedback”) sent to Teradata Corporation will be deemed non-confidential. Teradata Corporation will have no obligation of any kind with respect to Feedback and will be free to use, reproduce, disclose, exhibit, display, transform, create derivative works of, and distribute the Feedback and derivative works thereof without limitation on a royalty-free basis. Further, Teradata Corporation will be free to use any ideas, concepts, know-how, or techniques contained in such Feedback for any purpose whatsoever, including developing, manufacturing, or marketing products or services incorporating Feedback. Copyright © 1999-2013 by Teradata Corporation. All Rights Reserved. Preface Purpose This volume describes how to use the modeling, scoring and statistical test features of the Teradata Warehouse Miner product. Teradata Warehouse Miner is a set of Microsoft .NET interfaces and a multi-tier User Interface that together help understand the quality of data residing in a Teradata database, create analytic data sets, and build and score analytic models directly in the Teradata database. Audience This manual is written for users of Teradata Warehouse Miner, who should be familiar with Teradata SQL, the operation and administration of the Teradata RDBMS system and statistical techniques. They should also be familiar with the Microsoft Windows operating environment and standard Microsoft Windows operating techniques. Revision Record The following table lists a history of releases where this guide has been revised: Release Date Description TWM 5.3.3 06/30/12 Maintenance Release TWM 5.3.2 06/01/11 Maintenance Release TWM 5.3.1 06/30/10 Maintenance Release TWM 5.3.0 10/30/09 Feature Release TWM 5.2.2 02/05/09 Maintenance Release TWM 5.2.1 12/15/08 Maintenance Release TWM 5.2.0 05/31/08 Feature Release TWM 5.1.1 01/23/08 Maintenance Release TWM 5.1.0 07/12/07 Feature Release TWM 5.0.1 11/16/06 Maintenance Release TWM 5.0.0 09/22/06 Major Release Teradata Warehouse Miner User Guide - Volume 3 iii Preface How This Manual Is Organized How This Manual Is Organized This manual is organized and presents information as follows: • Chapter 1: “Analytic Algorithms” — describes how to use the Teradata Warehouse Miner Multivariate Statistics and Machine Learning Algorithms. This includes Linear Regression, Logistic Regression, Factor Analysis, Decision Trees, Clustering, Association Rules and Neural Network algorithms. • Chapter 2: “Scoring” — describes how to use the Teradata Warehouse Miner Multivariate Statistics and Machine Learning Algorithms scoring analyses. Scoring is available for Linear Regression, Logistic Regression, Factor Analysis, Decision Trees, Clustering and Neural Networks • Chapter 3: “Statistical Tests” — describes how to use Teradata Warehouse Miner Statistical Tests. This includes Binomial, Kolmogorov Smirnov, Parametric, Rank, and Contingency Tables-based tests. Conventions Used In This Manual The following typographical conventions are used in this guide: Convention Description Italic Titles (esp. screen names/titles) New terms for emphasis Monospace Code sample Output ALL CAPS Acronyms Bold Important term or concept GUI Item Screen item and/or esp. something you will click on or highlight in following a procedure. Related Documents Related Teradata documentation and other sources of information are available from: http://www.info.teradata.com Additional technical information on data warehousing and other topics is available from: http://www.teradata.com/t/resources Support Information Services, support and training information is available from: iv Teradata Warehouse Miner User Guide - Volume 3 Preface Related Documents http://www.teradata.com/services-support Teradata Warehouse Miner User Guide - Volume 3 v Preface Related Documents vi Teradata Warehouse Miner User Guide - Volume 3 Table of Contents Preface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii Purpose . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii Audience . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii Revision Record . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iii How This Manual Is Organized . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv Conventions Used In This Manual. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv Related Documents. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv Support Information . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . iv Chapter 1: Analytic Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Overview. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Association Rules . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Initiate an Association Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 Association - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 Association - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 Association - INPUT - Expert Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 Association - OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Run the Association Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 Results - Association Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 Tutorial - Association Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 Cluster Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 Options - Cluster Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 Success Analysis - Cluster Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 Using the TWM Cluster Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 Optimizing Performance of Clustering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 Initiate a Cluster Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 Cluster - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 Cluster - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 Cluster - INPUT - Expert Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 Cluster - OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 Run the Cluster Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 Teradata Warehouse Miner User Guide - Volume 3 vii Table of Contents Results - Cluster Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 Tutorial - Cluster Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 Decision Trees . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Initiate a Decision Tree Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Decision Tree - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Decision Tree - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Decision Tree - INPUT - Expert Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Run the Decision Tree Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Results - Decision Tree . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Tutorial - Decision Tree . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36 36 41 41 43 44 45 45 54 Factor Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Initiate a Factor Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Factor - INPUT - Data Selection. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Factor - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Run the Factor Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Results - Factor Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Tutorial - Factor Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 58 67 68 69 72 72 82 Linear Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 Initiate a Linear Regression Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95 Linear Regression - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 Linear Regression - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97 Linear Regression - OUTPUT. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 Run the Linear Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100 Results - Linear Regression. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101 Tutorial - Linear Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107 Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Initiate a Logistic Regression Function. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Logistic Regression - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Logistic Regression - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . Logistic Regression - INPUT - Expert Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Logistic Regression - OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Run the Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Results - Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Tutorial - Logistic Regression. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114 114 120 121 122 124 125 127 127 134 Neural Networks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Initiate a Neural Networks Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Neural Networks - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141 141 157 158 viii Teradata Warehouse Miner User Guide - Volume 3 Neural Networks - INPUT - Network Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159 Neural Networks - INPUT - Network Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160 Neural Networks - INPUT - MLP Activation Functions . . . . . . . . . . . . . . . . . . . . . . . . 161 Neural Networks - INPUT - Sampling. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162 Run the Neural Networks. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163 Results - Neural Networks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163 Tutorial - Neural Networks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166 Chapter 2: Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201 Overview. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201 Cluster Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201 Initiate Cluster Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 202 Cluster Scoring - INPUT - Data Selection. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203 Cluster Scoring - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 204 Cluster Scoring - OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205 Run the Cluster Scoring Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205 Results - Cluster Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206 Tutorial - Cluster Scoring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 208 Tree Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209 Initiate Tree Scoring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209 Tree Scoring - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210 Tree Scoring - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 211 Tree Scoring - OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213 Run the Tree Scoring Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213 Results - Tree Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213 Tutorial - Tree Scoring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 218 Factor Scoring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219 Initiate Factor Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 220 Factor Scoring - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221 Factor Scoring - INPUT - Analysis Parameters. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 222 Factor Scoring - OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223 Run the Factor Scoring Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224 Results - Factor Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224 Tutorial - Factor Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 226 Linear Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228 Initiate Linear Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228 Linear Scoring - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 229 Linear Scoring - INPUT - Analysis Parameters. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 230 Linear Scoring - OUTPUT. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231 Run the Linear Scoring Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232 Teradata Warehouse Miner User Guide - Volume 3 ix Table of Contents Results - Linear Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232 Tutorial - Linear Scoring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 234 Logistic Scoring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Initiate Logistic Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Logistic Scoring - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Logistic Scoring - INPUT - Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Logistic Scoring - OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Run the Logistic Scoring Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Results - Logistic Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Tutorial - Logistic Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 236 239 240 241 242 243 243 246 Neural Networks Scoring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Initiate Neural Networks Scoring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Neural Networks Scoring - INPUT - Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . Neural Networks Scoring - OUTPUT. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Run the Neural Networks Scoring Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Results - Neural Networks Scoring. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Neural Networks Scoring Tutorial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249 249 250 252 253 253 255 Chapter 3: Statistical Tests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 257 Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 257 Summary of Tests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 258 Data Requirements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 259 Parametric Tests. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Two Sample T-Test for Equal Means . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . F-Test - N-Way . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . F-Test/Analysis of Variance - Two Way Unequal Sample Size. . . . . . . . . . . . . . . . . . 261 262 269 279 Binomial Tests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 286 Binomial/Ztest. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287 Binomial Sign Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 293 Kolmogorov-Smirnov Tests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Kolmogorov-Smirnov Test (One Sample) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Lilliefors Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Shapiro-Wilk Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . D'Agostino and Pearson Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Smirnov Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 299 299 305 311 317 323 Tests Based on Contingency Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329 Chi Square Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329 Median Test. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336 Rank Tests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342 Mann-Whitney/Kruskal-Wallis Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342 x Teradata Warehouse Miner User Guide - Volume 3 Wilcoxon Signed Ranks Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 351 Friedman Test with Kendall's Coefficient of Concordance & Spearman's Rho . . . . . . 358 Appendix A: References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 367 Teradata Warehouse Miner User Guide - Volume 3 xi Table of Contents xii Teradata Warehouse Miner User Guide - Volume 3 List of Figures Figure 1: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 Figure 2: Add New Analysis dialog . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 Figure 3: Association > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 Figure 4: Association > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 Figure 5: Association: X to X. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 Figure 6: Association Combinations pane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 Figure 7: Association > Input > Expert Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 Figure 8: Association > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 Figure 9: Association > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 Figure 10: Association > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 Figure 11: Association > Results > Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 Figure 12: Association Graph Selector. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 Figure 13: Association Graph. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 Figure 14: Association Graph: Tutorial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 Figure 15: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 Figure 16: Add New Analysis dialog . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 Figure 17: Clustering > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 Figure 18: Clustering > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 Figure 19: Clustering > Input > Expert Options. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 Figure 20: Cluster > OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 Figure 21: Clustering > Results > Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 Figure 22: Clustering > Results > Sizes Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 Figure 23: Clustering > Results > Similarity Graph. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32 Figure 24: Clustering Analysis Tutorial: Sizes Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 Figure 25: Clustering Analysis Tutorial: Similarity Graph . . . . . . . . . . . . . . . . . . . . . . . . . . 36 Figure 26: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 Figure 27: Add New Analysis dialog . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 Figure 28: Decision Tree > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42 Figure 29: Decision Tree > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 Figure 30: Decision Tree > Input > Expert Options. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 Figure 31: Tree Browser. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 Figure 32: Tree Browser menu: Small Navigation Tree . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 Teradata Warehouse Miner User Guide - Volume 3 xiii List of Figures Figure 33: Tree Browser menu: Zoom Tree . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 Figure 34: Tree Browser menu: Print . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49 Figure 35: Text Tree . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 Figure 36: Rules List . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 Figure 37: Counts and Distributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 Figure 38: Tree Pruning menu. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 Figure 39: Tree Pruning Menu > Prune Selected Branch . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 Figure 40: Tree Pruning menu (All Options Enabled) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 Figure 41: Decision Tree Graph: Previously Pruned Tree . . . . . . . . . . . . . . . . . . . . . . . . . . 53 Figure 42: Decision Tree Graph: Predicate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 Figure 43: Decision Tree Graph: Lift . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 Figure 44: Decision Tree Graph Tutorial: Browser. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 Figure 45: Decision Tree Graph Tutorial: Lift . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 Figure 46: Decision Tree Graph Tutorial: Browser. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 Figure 47: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 Figure 48: Add New Analysis dialog . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 Figure 49: Factor Analysis > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 Figure 50: Factor Analysis > Input > Analysis Parameters. . . . . . . . . . . . . . . . . . . . . . . . . . 70 Figure 51: Factor Analysis > Results > Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72 Figure 52: Factor Analysis > Results > Pattern Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81 Figure 53: Factor Analysis > Results > Scree Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81 Figure 54: Factor Analysis Tutorial: Scree Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86 Figure 55: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95 Figure 56: Add New Analysis dialog . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 Figure 57: Linear Regression > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 Figure 58: Linear Regression > Input > Analysis Parameters. . . . . . . . . . . . . . . . . . . . . . . . 97 Figure 59: Linear Regression > OUTPUT. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 Figure 60: Linear Regression Tutorial: Linear Weights Graph. . . . . . . . . . . . . . . . . . . . . . 112 Figure 61: Linear Regression Tutorial: Scatter Plot (2d) . . . . . . . . . . . . . . . . . . . . . . . . . . 113 Figure 62: Linear Regression Tutorial: Scatter Plot (3d) . . . . . . . . . . . . . . . . . . . . . . . . . . 113 Figure 63: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120 Figure 64: Add New Analysis dialog . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121 Figure 65: Logistic Regression > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . 121 Figure 66: Logistic Regression > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . 122 Figure 67: Logistic Regression > Input > Expert Options. . . . . . . . . . . . . . . . . . . . . . . . . . 124 Figure 68: Logistic Regression > OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125 xiv Teradata Warehouse Miner User Guide - Volume 3 List of Figures Figure 69: Logistic Regression Tutorial: Logistic Weights Graph . . . . . . . . . . . . . . . . . . . 140 Figure 70: Logistic Regression Tutorial: Lift Chart. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141 Figure 71: Single Neuron System (schematic) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143 Figure 72: Parametric Model vs. Non-Parametric Model (schematic). . . . . . . . . . . . . . . . . 145 Figure 73: Fully connected MLP2 neural network with three inputs (schematic) . . . . . . . . 147 Figure 74: MLP vs. RBF neural networks in two dimensional input data (schematic) . . . . 148 Figure 75: RBF Neural Network with three inputs (schematic). . . . . . . . . . . . . . . . . . . . . . 148 Figure 76: Neural Network Training with early stopping (schematic) . . . . . . . . . . . . . . . . 154 Figure 77: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157 Figure 78: Add New Analysis dialogue . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158 Figure 79: Neural Network > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158 Figure 80: Neural Network > Input > Network Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159 Figure 81: Neural Network > Input > Network Parameters . . . . . . . . . . . . . . . . . . . . . . . . . 160 Figure 82: Neural Network > Input > MLP Activation Functions . . . . . . . . . . . . . . . . . . . . 161 Figure 83: Neural Network > Input > Sampling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162 Figure 84: Neural Network Tutorial 1: Data Selection Tab . . . . . . . . . . . . . . . . . . . . . . . . . 167 Figure 85: Neural Network Tutorial 1: Network Types Tab . . . . . . . . . . . . . . . . . . . . . . . . 168 Figure 86: Neural Network Tutorial 1: Network Parameters Tab . . . . . . . . . . . . . . . . . . . . 169 Figure 87: Neural Network Tutorial 1: MLP Activation Functions Tab . . . . . . . . . . . . . . . 170 Figure 88: Neural Network Tutorial 1: Sampling tab. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171 Figure 89: Neural Networks Tutorial 1: Results tab - Reports button . . . . . . . . . . . . . . . . . 172 Figure 90: Neural Networks Tutorial 1: Reports - Neural Network Summary . . . . . . . . . . 173 Figure 91: Neural Networks Tutorial 1: Reports - Correlation Coefficients . . . . . . . . . . . . 174 Figure 92: Neural Networks Tutorial 1: Reports - Data Statistics . . . . . . . . . . . . . . . . . . . . 175 Figure 93: Neural Networks Tutorial 1: Reports - Weights . . . . . . . . . . . . . . . . . . . . . . . . . 176 Figure 94: Neural Networks Tutorial 1: Reports - Sensitivity Analysis . . . . . . . . . . . . . . . 177 Figure 95: Neural Networks Tutorial 1: Results tab - Graph button . . . . . . . . . . . . . . . . . . 178 Figure 96: Neural Networks Tutorial 1: Graph - Histogram . . . . . . . . . . . . . . . . . . . . . . . . 179 Figure 97: Neural Networks Tutorial 1: Graph - Target Output . . . . . . . . . . . . . . . . . . . . . 180 Figure 98: Neural Networks Tutorial 1: Graph - X, Y and Z. . . . . . . . . . . . . . . . . . . . . . . . 181 Figure 99: Neural Networks Tutorial 2: Data Selection tab . . . . . . . . . . . . . . . . . . . . . . . . . 182 Figure 100: Neural Networks Tutorial 2: Network Types tab . . . . . . . . . . . . . . . . . . . . . . . 183 Figure 101: Neural Networks Tutorial 2: Network Parameters tab . . . . . . . . . . . . . . . . . . . 184 Figure 102: Neural Networks Tutorial 2: MLP Activation Functions tab . . . . . . . . . . . . . . 185 Figure 103: Neural Networks Tutorial 2: Sampling tab . . . . . . . . . . . . . . . . . . . . . . . . . . . . 186 Figure 104: Neural Networks Tutorial 2: Results tab - Reports button . . . . . . . . . . . . . . . . 188 Teradata Warehouse Miner User Guide - Volume 3 xv List of Figures Figure 105: Neural Networks Tutorial 2: Results - Neural Network Summary . . . . . . . . . 189 Figure 106: Neural Networks Tutorial 2: Reports - Data Statistics. . . . . . . . . . . . . . . . . . . 190 Figure 107: Neural Networks Tutorial 2: Reports - Weights . . . . . . . . . . . . . . . . . . . . . . . 191 Figure 108: Neural Networks Tutorial 2: Reports - Sensitivity Analysis . . . . . . . . . . . . . . 192 Figure 109: Neural Networks Tutorial 2: Reports - Confusion Matrix . . . . . . . . . . . . . . . . 193 Figure 110: Neural Networks Tutorial 2: Reports - Classification Summary . . . . . . . . . . . 194 Figure 111: Neural Networks Tutorial 2: Reports - Confidence Levels . . . . . . . . . . . . . . . 195 Figure 112: Neural Networks Tutorial 2: Results tab - Graph button . . . . . . . . . . . . . . . . . 196 Figure 113: Neural Networks Tutorial 2: Graph - Histogram . . . . . . . . . . . . . . . . . . . . . . . 197 Figure 114: Neural Networks Tutorial 2: Graph - Income vs. Age. . . . . . . . . . . . . . . . . . . 198 Figure 115: Neural Networks Tutorial 2: Graph - Lift Charts. . . . . . . . . . . . . . . . . . . . . . . 199 Figure 116: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 202 Figure 117: Add New Analysis > Scoring > Cluster Scoring . . . . . . . . . . . . . . . . . . . . . . . 203 Figure 118: Add New Analysis > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . 203 Figure 119: Add New Analysis > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . 204 Figure 120: Cluster Scoring > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205 Figure 121: Cluster Scoring > Results > Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206 Figure 122: Cluster Scoring > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206 Figure 123: Cluster Scoring > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 207 Figure 124: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209 Figure 125: Add New Analysis > Scoring > Tree Scoring . . . . . . . . . . . . . . . . . . . . . . . . . 210 Figure 126: Tree Scoring > Input > Data Selection. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210 Figure 127: Tree Scoring > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . 211 Figure 128: Tree Scoring > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213 Figure 129: Tree Scoring > Results > Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214 Figure 130: Tree Scoring > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215 Figure 131: Tree Scoring > Results > Lift Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 217 Figure 132: Tree Scoring > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 217 Figure 133: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221 Figure 134: Add New Analysis > Scoring > Factor Scoring. . . . . . . . . . . . . . . . . . . . . . . . 221 Figure 135: Factor Scoring > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 222 Figure 136: Factor Scoring > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . 223 Figure 137: Factor Scoring > Output. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223 Figure 138: Factor Scoring > Results > Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224 Figure 139: Factor Scoring > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225 Figure 140: Factor Scoring > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 226 xvi Teradata Warehouse Miner User Guide - Volume 3 List of Figures Figure 141: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 229 Figure 142: Add New Analysis > Scoring > Linear Scoring . . . . . . . . . . . . . . . . . . . . . . . . 229 Figure 143: Linear Scoring > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 230 Figure 144: Linear Scoring > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . 231 Figure 145: Linear Scoring > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231 Figure 146: Linear Scoring > Results > Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232 Figure 147: Linear Scoring > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233 Figure 148: Linear Scoring > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 234 Figure 149: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239 Figure 150: Add New Analysis > Scoring > Logistic Scoring. . . . . . . . . . . . . . . . . . . . . . . 240 Figure 151: Logistic Scoring > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . 240 Figure 152: Logistic Scoring > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . 241 Figure 153: Logistic Scoring > Output. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 242 Figure 154: Logistic Scoring > Results > Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 244 Figure 155: Logistic Scoring > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 244 Figure 156: Logistic Scoring > Results > Lift Graph. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 245 Figure 157: Logistic Scoring > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 245 Figure 158: Logistic Scoring Tutorial: Lift Graph . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249 Figure 159: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249 Figure 160: Add New Analysis > Scoring > Neural Net Scoring . . . . . . . . . . . . . . . . . . . . 250 Figure 161: Neural Networks Scoring > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . 251 Figure 162: Neural Networks Scoring > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 252 Figure 163: Neural Networks Scoring > Results > Reports . . . . . . . . . . . . . . . . . . . . . . . . . 253 Figure 164: Neural Networks Scoring > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . 254 Figure 165: Neural Networks Scoring > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . 255 Figure 166: Neural Networks Scoring Tutorial: Report. . . . . . . . . . . . . . . . . . . . . . . . . . . . 256 Figure 167: Neural Networks Scoring Tutorial: Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 256 Figure 168: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 263 Figure 169: Add New Analysis > Statistical Tests > Parametric Tests . . . . . . . . . . . . . . . . 263 Figure 170: T-Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264 Figure 171: T-Test > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 265 Figure 172: T-Test > Output. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 265 Figure 173: T-Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267 Figure 174: T-Test > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267 Figure 175: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270 Figure 176: Add New Analysis > Statistical Tests > Parametric Tests . . . . . . . . . . . . . . . . 270 Teradata Warehouse Miner User Guide - Volume 3 xvii List of Figures Figure 177: F-Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271 Figure 178: F-Test > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272 Figure 179: F-Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272 Figure 180: F-Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 273 Figure 181: F-Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274 Figure 182: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280 Figure 183: Add New Analysis > Statistical Tests > Parametric Tests. . . . . . . . . . . . . . . . 281 Figure 184: F-Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 281 Figure 185: F-Test > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 282 Figure 186: F-Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 283 Figure 187: F-Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 284 Figure 188: F-Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 284 Figure 189: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287 Figure 190: Add New Analysis > Statistical Tests > Binomial Tests . . . . . . . . . . . . . . . . . 288 Figure 191: Binomial Tests > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 288 Figure 192: Binomial Tests > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . 289 Figure 193: Binomial Tests > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 290 Figure 194: Binomial Tests > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291 Figure 195: Binomial Tests > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 291 Figure 196: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 293 Figure 197: Add New Analysis > Statistical Tests > Binomial Tests . . . . . . . . . . . . . . . . . 294 Figure 198: Binomial Sign Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . 294 Figure 199: Binomial Sign Test > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . 295 Figure 200: Binomial Sign Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 296 Figure 201: Binomial Sign Test > Results > SQL. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 297 Figure 202: Binomial Sign Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 297 Figure 203: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 299 Figure 204: Add New Analysis > Statistical Tests > Kolmogorov-Smirnov Tests. . . . . . . 300 Figure 205: Kolmogorov-Smirnov Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . 300 Figure 206: Kolmogorov-Smirnov Test > Input > Analysis Parameters. . . . . . . . . . . . . . . 301 Figure 207: Kolmogorov-Smirnov Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 302 Figure 208: Kolmogorov-Smirnov Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . 303 Figure 209: Kolmogorov-Smirnov Test > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . 303 Figure 210: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305 Figure 211: Add New Analysis> Statistical Tests > Kolmogorov-Smirnov Tests . . . . . . . 306 Figure 212: Lillefors Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 306 xviii Teradata Warehouse Miner User Guide - Volume 3 List of Figures Figure 213: Lillefors Test > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . 307 Figure 214: Lillefors Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 308 Figure 215: Lillefors Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 309 Figure 216: Lillefors Test > Results > Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 309 Figure 217: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 311 Figure 218: Add New Analysis > Statistical Tests > Kolmogorov-Smirnov Tests . . . . . . . 312 Figure 219: Shapiro-Wilk Test > Input > Data Selection. . . . . . . . . . . . . . . . . . . . . . . . . . . 312 Figure 220: Shapiro-Wilk Test > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . 313 Figure 221: Shapiro-Wilk Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314 Figure 222: Shapiro-Wilk Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315 Figure 223: Shapiro-Wilk Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 315 Figure 224: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 317 Figure 225: Add New Analysis > Statistical Tests > Kolmogorov-Smirnov Tests . . . . . . . 318 Figure 226: D'Agostino and Pearson Test > Input > Data Selection . . . . . . . . . . . . . . . . . . 318 Figure 227: D'Agostino and Pearson Test > Input > Analysis Parameters . . . . . . . . . . . . . 319 Figure 228: D'Agostino and Pearson Test > Output. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320 Figure 229: D'Agostino and Pearson Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . 321 Figure 230: D'Agostino and Pearson Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . 321 Figure 231: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323 Figure 232: Add New Analysis > Statistical Tests > Kolmogorov-Smirnov Tests . . . . . . . 324 Figure 233: Smirnov Test > Input > Data Selection. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 324 Figure 234: Smirnov Test > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . 325 Figure 235: Smirnov Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 326 Figure 236: Smirnov Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327 Figure 237: Smirnov Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327 Figure 238: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 330 Figure 239: Add New Analysis > Statistical Tests > Tests Based on Contingency Tables . 331 Figure 240: Chi Square Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . 331 Figure 241: Chi Square Test > Input > Analysis Parameters . . . . . . . . . . . . . . . . . . . . . . . . 332 Figure 242: Chi Square Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 333 Figure 243: Chi Square Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 334 Figure 244: Chi Square Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 334 Figure 245: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 337 Figure 246: Add New Analysis > Statistical Tests > Tests Based On Contingency Tables 337 Figure 247: Median Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 338 Figure 248: Median Test > Input > Analysis Parameters. . . . . . . . . . . . . . . . . . . . . . . . . . . 339 Teradata Warehouse Miner User Guide - Volume 3 xix List of Figures Figure 249: Median Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 339 Figure 250: Median Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 340 Figure 251: Median Test > Results > data. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 341 Figure 252: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 344 Figure 253: Add New Analysis > Statistical Tests > Rank Tests . . . . . . . . . . . . . . . . . . . . 344 Figure 254: Mann-Whitney/Kruskal-Wallis Test > Input > Data Selection . . . . . . . . . . . . 345 Figure 255: Mann-Whitney/Kruskal-Wallis Test > Input > Analysis Parameters . . . . . . . 346 Figure 256: Mann-Whitney/Kruskal-Wallis Test > Output. . . . . . . . . . . . . . . . . . . . . . . . . 346 Figure 257: Mann-Whitney/Kruskal-Wallis Test > Results > SQL . . . . . . . . . . . . . . . . . . 348 Figure 258: Mann-Whitney/Kruskal-Wallis Test > Results > data . . . . . . . . . . . . . . . . . . . 348 Figure 259: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 352 Figure 260: Add New Analysis > Statistical Tests > Rank Tests . . . . . . . . . . . . . . . . . . . . 353 Figure 261: Wilcoxon Signed Ranks Test > Input > Data Selection. . . . . . . . . . . . . . . . . . 353 Figure 262: Wilcoxon Signed Ranks Test > Input > Analysis Parameters . . . . . . . . . . . . . 354 Figure 263: Wilcoxon Signed Ranks Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 355 Figure 264: Wilcoxon Signed Ranks Test > Results > SQL . . . . . . . . . . . . . . . . . . . . . . . . 356 Figure 265: Wilcoxon Signed Ranks Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . 356 Figure 266: Add New Analysis from toolbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 359 Figure 267: Add New Analysis > Statistical Tests > Rank Tests . . . . . . . . . . . . . . . . . . . . 359 Figure 268: Friedman Test > Input > Data Selection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 360 Figure 269: Friedman Test > Input > Analysis Parameters. . . . . . . . . . . . . . . . . . . . . . . . . 361 Figure 270: Friedman Test > Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 361 Figure 271: Friedman Test > Results > SQL. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363 Figure 272: Friedman Test > Results > data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363 xx Teradata Warehouse Miner User Guide - Volume 3 List of Tables List of Tables Table 1: Three-Level Hierarchy Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 Table 2: Association Combinations output table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 Table 3: Tutorial - Association Analysis Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 Table 4: test_ClusterResults . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 Table 5: test_ClusterColumns. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 Table 6: Progress . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 Table 7: Solution. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 Table 8: Confusion Matrix Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 Table 9: Decision Tree Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55 Table 10: Variables: Dependent . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 Table 11: Variables: Independent. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 Table 12: Confusion Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 Table 13: Cumulative Lift Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 Table 14: Prime Factor Loadings report (Example) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65 Table 15: Prime Factor Variables report (Example). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66 Table 16: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67 Table 17: Factor Analysis Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 Table 18: Execution Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 Table 19: Eigenvalues. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 Table 20: Principal Component Loadings . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84 Table 21: Factor Variance to Total Variance Ratio . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 Table 22: Variance Explained By Factors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 Table 23: Difference . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 Table 24: Prime Factor Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 Table 25: Eigenvalues of Unit Scaled X'X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92 Table 26: Condition Indices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92 Table 27: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92 Table 28: Near Dependency report (example) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93 Table 29: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100 Table 30: Linear Regression Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108 Table 31: Regression vs. Residual . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108 Table 32: Execution Status . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108 Teradata Warehouse Miner User Guide - Volume 3 xxi List of Tables Table 33: Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 Table 34: Out . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109 Table 35: Model Assessment. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 Table 36: Columns In (Part 1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 Table 37: Columns In (Part 2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 Table 38: Columns In (Part 3) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111 Table 39: Columns Out . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111 Table 40: Logistic Regression - OUTPUT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126 Table 41: Logistic Regression Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135 Table 42: Execution Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136 Table 43: Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137 Table 44: Columns Out . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137 Table 45: Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138 Table 46: Columns Out . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138 Table 47: Prediction Success Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139 Table 48: Multi-Threshold Success Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139 Table 49: Cumulative Lift Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140 Table 50: Neuron Activation Functions for hidden/output neurons available in SANN. . . 149 Table 51: Output Database (Built by the Cluster Scoring analysis) . . . . . . . . . . . . . . . . . . 207 Table 52: Clustering Progress . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 208 Table 53: Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 208 Table 54: Confusion Matrix. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214 Table 55: Output Database table (Built by the Decision Tree Scoring analysis) . . . . . . . . 216 Table 56: Output Database table (Built by the Decision Tree Scoring analysis) - Create profiling tables option selected (“_1” appended) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216 Table 57: Output Database table (Built by the Decision Tree Scoring analysis) - Create profiling tables option selected (“_2” appended) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 217 Table 58: Decision Tree Model Scoring Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 218 Table 59: Confusion Matrix. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 218 Table 60: Cumulative Lift Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 218 Table 61: Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219 Table 62: Output Database table (Built by Factor Scoring) . . . . . . . . . . . . . . . . . . . . . . . . 225 Table 63: Factor Analysis Score Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 226 Table 64: Evaluation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 227 Table 65: Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 227 Table 66: Output Database table (Built by Linear Regression scoring) . . . . . . . . . . . . . . . 234 xxii Teradata Warehouse Miner User Guide - Volume 3 List of Tables Table 67: Linear Regression Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235 Table 68: Evaluation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235 Table 69: Data. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235 Table 70: Prediction Success Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 236 Table 71: Logistic Regression Multi-Threshold Success table . . . . . . . . . . . . . . . . . . . . . . 237 Table 72: Logistic Regression Cumulative Lift Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 238 Table 73: Output Database table (Built by Logistic Regression scoring) . . . . . . . . . . . . . . 244 Table 74: Logistic Regression Model Scoring Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246 Table 75: Prediction Success Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246 Table 76: Multi-Threshold Success Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247 Table 77: Cumulative Lift Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247 Table 78: Data. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 248 Table 79: Output Database table (Built by Neural Networks scoring). . . . . . . . . . . . . . . . . 254 Table 80: Statistical Test functions handling of input . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 259 Table 81: Two sample t tests for unpaired data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262 Table 82: Output Database table. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267 Table 83: T-Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268 Table 84: Output Columns - 1-Way F-Test Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274 Table 85: Output Columns - 2-Way F-Test Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274 Table 86: Output Columns - 3-Way F-Test Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 275 Table 87: F-Test (one-way) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 278 Table 88: Output Columns - 2-Way F-Test Analysis. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285 Table 89: F-Test (Two-way Unequal Cell Count) (Part 1). . . . . . . . . . . . . . . . . . . . . . . . . . 286 Table 90: F-Test (Two-way Unequal Cell Count) (Part 2). . . . . . . . . . . . . . . . . . . . . . . . . . 286 Table 91: F-Test (Two-way Unequal Cell Count) (Part 3). . . . . . . . . . . . . . . . . . . . . . . . . . 286 Table 92: Output Database table (Built by the Binomial Analysis) . . . . . . . . . . . . . . . . . . . 292 Table 93: Binomial Test Analysis (Table 1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 292 Table 94: Binomial Test Analysis (Table 2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 293 Table 95: Binomial Sign Analysis: Output Columns . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 298 Table 96: Tutorial - Binomial Sign Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 298 Table 97: Output Database table (Built by the Kolmogorov-Smirnov test analysis) . . . . . . 304 Table 98: Kolmogorov-Smirnov Test. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304 Table 99: Lilliefors Test Analysis: Output Columns . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310 Table 100: Lilliefors Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310 Table 101: Shapiro-Wilk Test Analysis: Output Columns. . . . . . . . . . . . . . . . . . . . . . . . . . 316 Table 102: Shapiro-Wilk Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 316 Teradata Warehouse Miner User Guide - Volume 3 xxiii List of Tables Table 103: D'Agostino and Pearson Test Analysis: Output Columns . . . . . . . . . . . . . . . . . 322 Table 104: D'Agostino and Pearson Test: Output Columns . . . . . . . . . . . . . . . . . . . . . . . . 322 Table 105: Smirnov Test Analysis: Output Columns . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 328 Table 106: Smirnov Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 328 Table 107: Chi Square Test Analysis: Output Columns . . . . . . . . . . . . . . . . . . . . . . . . . . . 335 Table 108: Chi Square Test (Part 1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336 Table 109: Chi Square Test (Part 2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336 Table 110: Median Test Analysis: Output Columns . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 341 Table 111: Median Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342 Table 112: Table for Mann-Whitney (if two groups) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 348 Table 113: Table for Kruskal-Wallis (if more than two groups). . . . . . . . . . . . . . . . . . . . . 349 Table 114: Mann-Whitney Test. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 349 Table 115: Kruskal-Wallis Test. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 350 Table 116: Mann-Whitney Test. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 351 Table 117: Wilcoxon Signed Ranks Test Analysis: Output Columns. . . . . . . . . . . . . . . . . 357 Table 118: Wilcoxon Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 357 Table 119: Friedman Test Analysis: Output Columns . . . . . . . . . . . . . . . . . . . . . . . . . . . . 363 Table 120: Friedman Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 365 xxiv Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Overview CHAPTER 1 Analytic Algorithms What’s In This Chapter For more information, see these subtopics: 1 “Overview” on page 1 2 “Association Rules” on page 2 3 “Cluster Analysis” on page 19 4 “Decision Trees” on page 36 5 “Factor Analysis” on page 58 6 “Linear Regression” on page 86 7 “Logistic Regression” on page 114 8 “Neural Networks” on page 141 Overview Teradata Warehouse Miner contains several analytic algorithms from both the traditional statistics and machine learning disciplines. These algorithms pertain to the exploratory data analysis (EDA) and model-building phases of the data mining process. Along with these algorithms, Teradata Warehouse Miner contains corresponding model scoring and evaluation functions that pertain to the model evaluation and deployment phases of the data mining process. A brief summary of the algorithms offered may be given as follows: • Linear Regression — Linear regression can be used to predict or estimate the value of a continuous numeric data element based upon a linear combination of other numeric data elements present for each observation. • Logistic Regression — Logistic regression can be used to predict or estimate a two-valued variable based upon other numeric data elements present for each observation. • Factor Analysis — Factor analysis is a collective term for a family of techniques. In general, Factor analysis can be used to identify, quantify, and re-specify the common and unique sources of variability in a set of numeric variables. One of its many applications allows an analytical modeler to reduce the number of numeric variables needed to describe a collection of observations by creating new variables, called factors, as linear combinations of the original variables. • Decision Trees — Decision trees, or rule induction, can be used to predict or estimate the value of a multi-valued variable based upon other categorical and continuous numeric data elements by building decision rules and presenting them graphically in the shape of a tree, based upon splits on specific data values. Teradata Warehouse Miner User Guide - Volume 3 1 Chapter 1: Analytic Algorithms Association Rules • Clustering — Cluster analysis can be used to form multiple groups of observations, such that each group contains observations that are very similar to one another, based upon values of multiple numeric data elements. • Association Rules — Generate association rules and various measures of frequency, relationship and statistical significance associated with these rules. These rules can be general, or have a dimension of time association with them. • Neural Networks — Neural Networks can be used to build a Regression model for predicting one or more continuous variables or a Classification model for predicting one or more categorical variables, using either a Multi-Layer Perceptron or a Radial Basis Function network. Note: Neural Networks are available only with the product TWM Neural Networks Addin Powered by STATISTICA. Association Rules Overview Association Rules are measurements on groups of observations or transactions that contain items of some kind. These measurements seek to describe the relationships between the items in the groups, such as the frequency of occurrence of items together in a group or the probability that items occur in a group given that other specific items are in that group. The nature of items and groups in association analysis and the meaning of the relationships between items in a group will depend on the nature of the data being studied. For example, the items may be products purchased and the groups the market baskets in which they were purchased. (This is generally called market basket analysis). Another example is that items may be accounts opened and the groups the customers that opened the accounts. This type of association analysis is useful in a cross-sell application to determine what products and services to sell with other products and services. Obviously the possibilities are endless when it comes to the assignment of meaning to items and groups in business and scientific transactions or observations. Rules What does an association analysis produce and what types of measurements does it include? An association analysis produces association rules and various measures of frequency, relationship and statistical significance associated with these rules. Association rules are of the form X 1 X 2 X n Y 1 Y 2 Y m where X 1 X 2 X n is a set of n items that appear in a group along with a set of m items Y 1 Y 2 Y m in the same group. For example, if checking, saving and credit card accounts are owned by a customer, then the customer will also own a certificate of deposit (CD) with a certain frequency. Relationship means that, for example, owning a specific account or set of accounts, (antecedent), is associated with ownership of one or more other specific accounts (consequent). Association rules, in and of themselves, do not warrant inferences of causality, however they may point to relationships among items or events that could be studied further using other analytical 2 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Association Rules techniques which are more appropriate for determining the structure and nature of causalities that may exist. Measures The four measurements made for association rules are support, confidence, lift and Z score. Support Support is a measure of the generality of an association rule, and is literally the percentage (a value between 0 and 1) of groups that contain all of the items referenced in the rule. More formally, in the association rule defined as L R , L represents the items given to occur together (the Left side or antecedent), and R represents the items that occur with them as a result (the Right side or consequent). Support can actually be applied to a single item or a single side of an association rule, as well as to an entire rule. The support of an item is simply the percentage of groups containing that item. Given the previous example of banking product ownership, let L be defined as the number of customers who own the set of products on the left side and let R be defined as the number of customers who own the set of products on the right side. Further, let LR be the number of customers who own all products in the association rule (note that this notation does not mean L times R), and let N be defined as the total number of customers under consideration. The support of L, R and the association rule are given by: L Sup L = ---N R Sup R = ---N LR Sup L R = -------N Let’s say for example that out of 10 customers, 6 of them have a checking account, 5 have a savings account, and 4 have both. If L is (checking) and R is (savings), then Sup L is .6, Sup R is .5 and Sup L R is .4. Confidence Confidence is the probability of R occurring in an item group given that L is in the item group. The equation to calculate the probability of R occurring in an item group given that L is in the item group is given by: L R Conf L R = Sup --------------------Sup L Another way of expressing the measure confidence is as the percentage of groups containing L that also contain R. This gives the following equivalent calculation for confidence: LR Conf L R = -------L Teradata Warehouse Miner User Guide - Volume 3 3 Chapter 1: Analytic Algorithms Association Rules Using the previous example of banking product ownership once again, the confidence that checking account ownership implies savings account ownership is 4/6. The expected value of an association rule is the number of customers that are expected to have both L and R if there is no relationship between L and R. (To say that there is no relationship between L and R means that customers who have L are neither more likely nor less likely to have R than are customers who do not have L). The equation for the expected value of the association rule is: LR E_LR = -----------N An equivalent formula for the expected value of the association rule is: E_LR = Sup L Sup R N Again using the previous example, the expected value of the number of customers with checking and savings is calculated as 6 * 5 / 10 or 3. The expected confidence of a rule is the confidence that would result if there were no relationship between L and R. This simply equals the percentage of customers that own R, since if owning L has no effect on owning R, then it would be expected that the percentage of L’s that own R would be the same as the percentage of the entire population that own R. The following equation computes expected confidence: R E_Conf = ---- = Sup R N From the previous example, the expected confidence that checking implies savings is given by 5/10. Lift Lift measures how much the probability of R is increased by the presence of L in an item group. A lift of 1 indicates there are exactly as many occurrences of R as expected; thus, the presence of L neither increases nor decreases the likelihood of R occurring. A lift of 5 indicates that the presence of L implies that it is 5 times more likely for R to occur than would otherwise be expected. A lift of 0.5 indicates that when L occurs, it is one half as likely that R will occur. Lift can be calculated as follows: LR Lift L R = --------------E_LR From another viewpoint, lift measures the ratio of the actual confidence to the expected confidence, and can be calculated equivalently as either of the following: L R Lift L R = Conf --------------------E_Conf Conf L R Lift L R = ---------------------------------Sup R 4 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Association Rules The lift associated with the previous example of “checking implies savings” is 4/3. Z score Z score measures how statistically different the actual result is from the expected result. A Z score of zero corresponds to the situation where the actual number equals the expected. A Z score of 1 means that the actual number is 1 standard deviation greater than expected. A Z score of -3.0 means that the actual number is 3 standard deviations less than expected. As a rule of thumb, a Z score greater than 3 (or less than -3) indicates a statistically significant result, which means that a difference that large between the actual result and the expected is very unlikely to be due to chance. A Z score attempts to help answer the question of how confident you can be about the observed relationship between L and R, but does not directly indicate the magnitude of the relationship. It is interesting to note that a negative Z score indicates a negative association. These are rules L R where ownership of L decreases the likelihood of owning R. The following equation calculates a measure of the difference between the expected number of customers that have both L and R, if there is no relationship between L and R, and the actual number of customers that have both L and R. (It can be derived starting with either the formula for the standard deviation of the sampling distribution of proportions or the formula for the standard deviation of a binomial variable). LR – E_LR Zscore L R = --------------------------------------------------------------E_LR SQRT E_LR(1 – -------------- N or equivalently: N Sup LR – N Sup L Sup R Zscore L R = -------------------------------------------------------------------------------------------------------N Sup L Sup R 1 – Sup L Sup R The mean value is E_LR, and the actual value is LR. The standard deviation is calculated with SQRT (E_LR * (1 - E_LR/N)). From the previous example, the expected value is 6 * 5 / 10, so the mean value is 3. The actual value is calculated knowing that savings and checking accounts are owned by 4 out of 10 customers. The standard deviation is SQRT(3*(1-3/10)) or 1.449. The Z score is therefore (4 - 3) / 1.449 = .690. Interpreting Measures None of the measures described above are “best”; they all measure slightly different things. In the discussion below, product ownership association analysis is used as an example for purposes of illustration. First look at confidence, which measures the strength of an association: what percent of L customers also own R? Many people will sort associations by confidence and consider the highest confidence rules to be the best. However, there are several other factors to consider. One factor to consider is that a rule may apply to very few customers, so is not very useful. This is what support measures, the generality of the rule, or how often it applies. Thus a rule L R might have a confidence of 70%, but if that is just 7 out of 100 customers, it has Teradata Warehouse Miner User Guide - Volume 3 5 Chapter 1: Analytic Algorithms Association Rules very low support and is not very useful. Another shortcoming of confidence is that by itself it does not tell you whether owning L “changes” the likelihood of owning R, which is probably the more important piece of information. For example, if 20% of the customers own R, then a rule L R (20% of those with L also own R) may have high confidence but is really providing no information, because customers that own L have the same rate of ownership of R as the entire population does. What is probably really wanted is to find the products L for which the confidence of L R is significantly greater than 20%. This is what lift measures, the difference between the actual confidence and the expected confidence. However, lift, like confidence, is much less meaningful when very small numbers are involved; that is, when the support is low. If the expected number is 2 and there are actually 8 customers with product R, then the lift is an impressive 400. But because of the small numbers involved, the association rule is likely of limited use, and might even have occurred by chance. This is where the Z score comes in. For a rule L R , confidence indicates the likelihood that R is owned given that L is owned. Lift indicates how much owning L increases or decreases the probability of the ownership of R, and Z score measures how trustworthy the observed difference between the actual and expected ownership is relative to what could be observed due to chance alone. For example, for a rule L R , if it is expected to have 10,000 customers with both L and R, and there are actually 11,000, the lift would be only 1.1, but the Z score would be very high, because such a large difference could not be due to chance. Thus, a large Z score and small lift means there definitely is an effect, but it is small. A large lift and small Z means there appears to be a large effect, but it might not be real. A possible strategy then is given here as an illustration, but the exact strategy and threshold values will depend on the nature of each business problem addressed with association analysis. The full set of rules produced by an association analysis is often too large to examine in detail. First, prune out rules that have low Z scores. Try throwing out rules with a Z score of less than 2, if not 3, 4 or 5. However, there is little reason to focus in on rules with extremely high Z scores. Next, filter according to support and lift. Setting a limit on the Z score will not remove rules with low support or with low lift that involve common products. Where to set the support threshold depends on what products are of interest and performance considerations. Where to set the lift threshold is not really a technical question, but a question of preference as to how large a lift is useful from a business perspective. A lift of 1.5 for L R means that customers that own L are 50% more likely to own R than among the overall population. If a value of 1.5 does not yield interesting results, then set the threshold higher. Sequence Analysis Sequence analysis is a form of association analysis where the items in an association rule are considered to have a time ordering associated with them. By default, when sequence analysis is requested, left side items are assumed to have “occurred” before right side items, and in fact the items on each side of an association rule, left or right, are also time ordered within themselves. If we use in a sequence analysis the more full notation for an association rule L R , namely X 1 X 2 X m Y 1 Y 2 Y n , then we are asserting that not only do the X items precede the Y items, but X 1 precedes X 2 , which precedes X· m , which precedes Y 1, which precedes Y 2 , which precedes Y n . 6 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Association Rules It is important to note here that if a strict ordering of items in a sequence analysis is either not desired or not possible for some reason (such as multiple purchases on the same day), an option is provided to relax the strict ordering. With relaxed sequence analysis, all items on the left must still precede all items on the right of a sequence rule, but the items on the left and the items on the right are not time ordered amongst themselves. (When the rules are presented, the items in each rule are ordered by name for convenience). Lift and Z score are calculated differently for sequence analysis than for association analysis. Recall that the expected value of the association rule, E_LR, is given by Sup (L) * Sup (R) * N for a non-sequence association analysis. For example, if L occurs half the time and R occurs half the time, then if L and R are independent of each other it can be expected that L and R will occur together one-fourth of the time. But this does not take into account the fact that with sequence analysis, the correct ordering can only be expected to happen some percentage of the time if L and R are truly independent of each other. Interestingly, this expected percentage of independent occurrence of correct ordering is calculated the same for strictly ordered and relaxed ordered sequence analysis. With m items on the left and n on the right, the probability of correct ordering is given by “m!n!/(m + n)!”. Note that this is the inverse of the combinatorial analysis formula for the number of permutations of m + n objects grouped such that m are alike and n are alike. In the case of strictly ordered sequence analysis, the applicability of the formula just given for the probability of correct ordering can be explained as follows. There are clearly m + n objects in the rule, and saying that m are alike and n are alike corresponds to restricting the permutations to those that preserve the ordering of the m items on the left side and the n items on the right side of the rule. That is, all of the orderings of the items on a side other than the correct ordering fall out as being the same permutation. The logic of the formula given for the probability of correct ordering is perhaps easier to see in the case of relaxed ordering. Since there are m + n items in the rule there are (m + n)! possible orderings of the items. Out of these, there are m! ways the left items can be ordered and n! ways the right items can be ordered while insuring that the m items on the left precede the n items on the right, so there are m!n! valid orderings out of the (m + n)! possible. The “probability of correct ordering” factor described above has a direct effect on the calculation of lift and Z score. Lift is effectively divided by this factor, such that a factor of one half results in doubling the lift and increasing the Z score as well. The resulting lift and Z score for sequence analysis must be interpreted cautiously however since the assumptions made in calculating the independent probability of correct ordering are quite broad. For example, it is assumed that all combinations of ordering are equally likely to occur, and the amount of time between occurrences is completely ignored. To give the user more control over the calculation of lift and Z score for a sequence analysis, an option is provided to set the “probability of correct ordering” factor to a constant value if desired. Setting it to 1 for example effectively ignores this factor in the calculation of E_LR and therefore in lift and Z score. Initiate an Association Analysis Use the following procedure to initiate a new Association analysis in Teradata Warehouse Miner: Teradata Warehouse Miner User Guide - Volume 3 7 Chapter 1: Analytic Algorithms Association Rules 1 Click on the Add New Analysis icon in the toolbar: Figure 1: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Analytics under Categories and then under Analyses double-click on Association: Figure 2: Add New Analysis dialog 3 This will bring up the Association dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Association - INPUT - Data Selection On the Association dialog click on INPUT and then click on data selection: Figure 3: Association > Input > Data Selection 8 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Association Rules On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for the Association analysis. • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can either insert columns as Group, Item, or Sequence columns. Make sure you have the correct portion of the window highlighted. • Group Column — The column that specifies the group for the Association analysis. This column should specify observations or transactions that contain items of some kind. • Item Column — The column that specifies the items to be analyzed in the Association analysis. The relationship of these items within the group will be described by the Association analysis. • Sequence Column — The column that specifies the sequence of items in the Association analysis. This column should have a time ordering relationship with the item associated with them. Association - INPUT - Analysis Parameters On the Association dialog click on INPUT and then click on analysis parameters: Teradata Warehouse Miner User Guide - Volume 3 9 Chapter 1: Analytic Algorithms Association Rules Figure 4: Association > Input > Analysis Parameters On this screen select: • Association Combinations — In this window specify one or more association combinations in the format of “X TO Y” where the sum of X and Y must not exceed a total of 10. First select an “X TO Y” combination from the drop-down lists: Figure 5: Association: X to X Then click the Add button to add this combination to the window. Repeat for as many combinations as needed: Figure 6: Association Combinations pane If needed, remove a combination by highlighting it in the window and then clicking on the Remove button. • Processing Options • Perform All Steps — Execute the entire Association/Sequence Analysis, regardless of result sets generated from a previous execution. • Perform Support Calculation Only — In order to determine the minimum support value to use, the user may choose to only build the single-item support table by using this option, making it possible to stop and examine the table before proceeding. • Recalculate Final Affinities Only — Rebuild just the final association tables using support tables from a previous run provided that intermediate work tables were not dropped (see Drop All Support Tables After Execution option below). • Auto-Calculate group count — By default, the algorithm automatically determines the actual input count. • 10 Force Group Count To — If the Auto-Calculate group count is disabled, this option can be used to fix the number of groups, overriding the actual input count. This is useful in conjunction with the Reduced Input Options, to set the group count to the Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Association Rules group count in the original data set, rather than the reduced input data set. • Drop All Support Tables After Execution — Normally, the Association analysis temporarily builds the support tables, dropping them prior to termination. If for performance reasons, it is desired to use the Recalculate Final Affinities Only option, this option can be disabled so that this clean-up of support tables does not happen. • Minimum Support — The minimum Support value that the association must have in order to be reported. Using this option reduces the input data - this can be saved for further processing using the Reduced Input Options. Using this option also invokes list-wise deletion, automatically removing from processing (and from the reduced input data) all rows containing a null Group, Item or Sequence column. • Minimum Confidence — The minimum Confidence value that the association must have in order to be reported. • Minimum Lift — The minimum Lift value that the association must have in order to be reported. • Minimum Z-Score — The minimum absolute Z-Score value that the association must have in order to be reported. • Sequence Options — If a column is specified with the Sequence Column option, then the following two Sequence Options are enabled. Note that Sequence Analysis is not available when Hierarchy Information is specified: • Use Relaxed Ordering — With this option, the items on each side of the association rule may be in any sequence provided all the left items (antecedents) precede all the right items (precedents). • Auto-Calculate Ordering Probability — Sequence analysis option to let the algorithm calculate the "probability of correct ordering" according to the principles described in “Sequence Analysis” on page 6. (Note that the following option to set "Ordering Probability" to a chosen value is only available if this option is unchecked). • Ordering Probability — Sequence analysis option to set probability of correct ordering to a non-zero constant value between 0 and 1. Setting it to a 1 effectively ignores this principle in calculating lift and Z-score. Association - INPUT - Expert Options On the Association dialog click on INPUT and then click on expert options: Figure 7: Association > Input > Expert Options On this screen select: • Where Conditions — An SQL WHERE clause may be specified here to provide further input filtering for only those groups or items that you are interested in. This works exactly Teradata Warehouse Miner User Guide - Volume 3 11 Chapter 1: Analytic Algorithms Association Rules like the Expert Options for the Descriptive Statistics, Transformation and Data Reorganization functions - only the condition itself is entered here. Using this option reduces the input data set - this can be saved for further processing using the Reduced Input Options. Using this option also invokes list-wise deletion, automatically removing from processing (and from the reduced input data) all rows containing a null Group, Item or Sequence column. • Include Hierarchy Table — A hierarchy lookup table may be specified to convert input items on both the left and right sides of the association rule to a higher level in a hierarchy if desired. Note that the column in the hierarchy table corresponding to the items in the input table must not contain repeated values, so effectively the items in the input table must match the lowest level in the hierarchy table. The following is an example of a threelevel hierarchy table compatible with Association analysis, provided the input table matches up with the column ITEM1. Table 1: Three-Level Hierarchy Table ITEM1 ITEM2 ITEM3 DESC1 DESC2 DESC3 A P Y Savings Passbook Deposit B P Y Checking Passbook Deposit C W Z Atm Electronic Access D S X Charge Short Credit E T Y CD Term Deposit F T Y IRA Term Deposit G L X Mortgage Long Credit H L X Equity Long Credit I S X Auto Short Credit J W Z Internet Electronic Access Using this option reduces the input data set - this can be saved for further processing using the Reduced Input Options. Using this option also invokes list-wise deletion, automatically removing from processing (and from the reduced input data) all rows containing a null Group, Item or Sequence column. The following columns in the hierarchy table must be specified with this option. • Item Column — The name of the column that can be joined to the column specified by the Item Column option on the Select Column tab to look up the associated Hierarchy. • Hierarchy Column — The name of the column with the Hierarchy values. • Include Description Table — For reporting purposes, a descriptive name or label can be given to the items processed during the Association/Sequence Analysis. • 12 Item ID Column — The name of the column that can be joined to the column specified by the Item Column option on the Select Column tab (or Hierarchy Column option on Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Association Rules the Hierarchies tab if hierarchy information is also specified) to look up the description. • Item Description Column — The name of the column with the descriptive values. • Include Left Side Lookup Table — A focus products table may be specified to process only those items that are of interest on the left side of the association. • Left Side Identifier Column — The name of the column where the Focus Products values exist for the left side of the association. • Include Right Side Lookup Table — A focus products table may be specified to process only those items that are of interest on the right side of the association. • Right Side Identifier Column — The name of the column where the Focus Products values exist for the right side of the association. Association - OUTPUT On the Association dialog click on OUTPUT: Figure 8: Association > Output On this screen select: • Output Tables • Database Name — The database where the Association analysis build temporary and permanent tables during the analysis. This defaults to the Result Database. • Table Names — Assign a table name for each displayed combination. • Advertise Output — The Advertise Output option “advertises” each output table (including the Reduced Input Table, if saved) by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Reduced Input Options — A reduced input set, based upon the minimum support value specified, a product hierarchy or input filtering via a WHERE clause, can be saved and used as input to a subsequent Association/Sequence analysis as follows: • Save Reduced Input Table — Check box to specify to the analysis that the reduced input table should be saved. • Database Name — The database name where the reduced input table will be saved. • Table Name — The table name that the reduced input table will be saved under. Teradata Warehouse Miner User Guide - Volume 3 13 Chapter 1: Analytic Algorithms Association Rules • Generate SQL, but do not Execute it — Generate the Association or Sequence Analysis SQL, but do not execute it - the set of queries are returned with the analysis results. Run the Association Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Association Analysis The results of running the Association analysis include a table for each association pair requested, as well as the SQL to perform the association or sequence analysis. All of these results are outlined below. Association - RESULTS - SQL On the Association dialog click on RESULTS and then click on SQL: Figure 9: Association > Results > SQL The series of SQL statements that comprise the Association/Sequence Analysis are displayed here. Association - RESULTS - data On the Association dialog click on RESULTS and then click on data: Figure 10: Association > Results > Data Results data, if any, is displayed in a data grid as described in “RESULTS Tab” on page 80 of the Teradata Warehouse Miner User Guide (Volume 1). An output table is generated for each item pair specified in the Association Combinations option. Each table generated has the form specified below: 14 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Association Rules Table 2: Association Combinations output table Name Type Definition ITEMXOFY User Defined Two or more columns will be generated, depending upon the number of Association Combinations. Together, these form the UPI of the result table. The value for X in the column name is 1 through the number of item pairs specified. The value for Y in the column name is the sum of the number of items specified. For example, specifying Left and Right Association Combinations or <1, 1> will produce two columns: ITEM1OF2, ITEM2OF2. Specifying <1,2> will result in three columns: ITEM1OF3, ITEM2OF3 and ITEM3OF3. The data type is the same as the Item Column. Default- Data type of Item Column LSUPPORT DECIMAL(18,5) The Support of the left-side item or antecedent only. RSUPPORT DECIMAL(18,5) The Support of the right-side item or consequent only. SUPPORT DECIMAL(18,5) The Support of the association (i.e. antecedent and consequent together). CONFIDENCE DECIMAL(18,5) The Confidence of the association. LIFT DECIMAL(15,5) The Lift of the association. ZSCORE DECIMAL(15,5) The Z-Score of the association. Association - RESULTS - graph On the Association dialog click on RESULTS and then click on graph: Figure 11: Association > Results > Graph For 1-to-1 Associations, a tile map is available as described below. (No graph is available for combinations other than 1-to-1). • Graph Options — Two selectors with a Reference Table display underneath are used to make association selections to graph. For example, the following selections produced the graph below. Teradata Warehouse Miner User Guide - Volume 3 15 Chapter 1: Analytic Algorithms Association Rules Figure 12: Association Graph Selector The Graph Options display has the following selectors: a Select item 1 of 2 from this table, then click button. The first step is to select the left-side or antecedent items to graph associations for by clicking or dragging the mouse just to the left of the row numbers displayed. Note that the accumulated minimum and maximum values of the measures checked just above the display are given in this table. (The third column, “Item2of2 count” is a count of the number of associations that are found in the result table for this left-side item). Once the selections are made, click the big button between the selectors. b Select from these tables to populate graph. The second step is to select once again the desired left-side or antecedent items by clicking or dragging the mouse just to the left of the row numbers displayed under the general header “Item 1 of 2” in the left-hand portion of selector 2. Note that as “Item 1 of 2” items are selected, “Item 2 of 2” right-side or consequent items are automatically selected in the right-hand portion of selector 2. Here the accumulated minimum and maximum values of the measures checked just above this display are given in the trailing columns of the table. (The third column “Item1of2 count” is a count of the number of associations that are found in the result table for this right-side item when limited to associations involving the left-side items selected in step 1). The corresponding associations are automatically highlighted in the Reference Table below. An alternative second step is to directly select one or more “Item 2 of 2" items in the right-hand portion of selector 2. The corresponding associations (again, limited to the left-side items selected in the first step) are then highlighted in the Reference Table below. 16 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Association Rules • Reference Table — This table displays the rows from the result table that correspond to the selections made above in step 1, highlighting the rows corresponding to the selections made in step 2. • (Row Number) — A sequential numbering of the rows in this display. • Item 1 of 2 — Left item or antecedent in the association rule. • Item 2 of 2 — Right item or consequent in the association rule. • LSupport — The left-hand item Support, calculated as the percentage (a value between 0 and 1) of groups that contain the left-hand item referenced in the association rule. • RSupport — The right-hand item Support, calculated as the percentage (a value between 0 and 1) of groups that contain the right-hand item referenced in the association rule. • Support — The Support, which is a measure of the generality of an association rule. Calculated as the percentage (a value between 0 and 1) of groups that contain all of the items referenced in the rule • Confidence — The Confidence defined as the probability of the right-hand item occurring in an item group given that the left-hand item is in the item group. • Lift — The Lift which measures how much the probability of the existence of the right-hand item is increased by the presence of the left hand item in a group. • ZScore — The Z score value, a measure of how statistically different the actual result is from the expected result. • Show Graph — A tile map is displayed when the “show graph” tab is selected, provided that valid “graph options” selections have been made. The example below corresponds to the graph options selected in the example above. Figure 13: Association Graph The tiles are color coded in the gradient specified on the right-hand side. Clicking on any tile, brings up all statistics associated with that association, and highlights the two items in Teradata Warehouse Miner User Guide - Volume 3 17 Chapter 1: Analytic Algorithms Association Rules the association. Radio buttons above the upper right hand corner of the tile map can be used to select the measure to color code in the tiles, that is either Support, Lift or Zscore. Tutorial - Association Analysis In this example, an Association analysis is performed on the fictitious banking data to analyze channel usage. Parameterize an Association analysis as follows: • Available Tables — twm_credit_tran • Group Column — cust_id • Item Column — channel • Association Combinations • Left — 1 • Right — 1 • Processing Options • Perform All Steps — Enabled • Minimum Support — 0 • Minimum Confidence — 0.1 • Minimum Lift — 1 • Minimum Z-Score — 1 • Where Clause Text — channel <> ‘ ‘ (i.e. channel is not equal to a single blank) • Output Tables • 1 to 1 Table Name — twm_tutorials_assoc Run the analysis, and click on Results when it completes. For this example, the Association analysis generated the following pages. The SQL is not shown for brevity. Table 3: Tutorial - Association Analysis Data ITEM1OF2 ITEM20F2 LSUPPORT RSUPPORT SUPPORT CONFIDENCE LIFT ZSCORE A E 0.85777 0.91685 0.80744 0.94132 1.02669 1.09511 B K 0.49672 0.35667 0.21007 0.42291 1.18572 1.84235 B V 0.49672 0.36324 0.22538 0.45374 1.24915 2.49894 C K 0.67177 0.35667 0.26477 0.39414 1.10506 1.26059 C V 0.67177 0.36324 0.27133 0.4039 1.11194 1.35961 E A 0.91685 0.85777 0.80744 0.88067 1.0267 1.09511 K B 0.35667 0.49672 0.21007 0.58898 1.18574 1.84235 K C 0.35667 0.67177 0.26477 0.74234 1.10505 1.26059 K V 0.35667 0.36324 0.1663 0.46626 1.28361 2.33902 V B 0.36324 0.49672 0.22538 0.62047 1.24913 2.49894 18 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis Table 3: Tutorial - Association Analysis Data ITEM1OF2 ITEM20F2 LSUPPORT RSUPPORT SUPPORT CONFIDENCE LIFT ZSCORE V C 0.36324 0.67177 0.27133 0.74697 1.11194 1.35961 V K 0.36324 0.35667 0.1663 0.45782 1.2836 2.33902 Click on Graph Options and perform the following steps: 1 Select all data in selector 1 under the “Item 1 of 2" heading. 2 Click on the large button between selectors 1 and 2. 3 Select all data in selector 2 under the “Item 1 of 2" heading. 4 Click on the show graph tab. When the tile map displays, perform the following additional steps: a Click on the bottom most tile. (Hovering over this tile will display the item names K and V). b Try selecting different measures at the top right of the tile map. (Zscore will initially be initially selected). Figure 14: Association Graph: Tutorial Cluster Analysis Overview The task of modeling multidimensional data sets encompasses a variety of statistical techniques, including that of ‘cluster analysis’. Cluster analysis is a statistical process for Teradata Warehouse Miner User Guide - Volume 3 19 Chapter 1: Analytic Algorithms Cluster Analysis identifying homogeneous groups of data objects. It is based on unsupervised machine learning and is crucial in data mining. Due to the massive sizes of databases today, implementation of any clustering algorithm must be scalable to complete analysis within a practicable amount of time, and must operate on large volumes of data with many variables. Typical clustering statistical algorithms do not work well with large databases due to memory limitations and execution times required. The advantage of the cluster analysis algorithm in Teradata Warehouse Miner is that it enables scalable data mining operations directly within the Teradata RDBMS. This is achieved by performing the data intensive aspects of the algorithm using dynamically generated SQL, while low-intensity processing is performed in Teradata Warehouse Miner. A second key design feature is that model application or scoring is performed by generating and executing SQL based on information about the model saved in metadata result tables. A third key design feature is the use of the Expectation Maximization or EM algorithm, a particularly sound statistical processing technique. Its simplicity makes possible a purely SQL-based implementation that might not otherwise be feasible with other optimization techniques. And finally, the Gaussian mixture model gives a probabilistic approach to cluster assignment, allowing observations to be assigned probabilities for inclusion in each cluster. The clustering is based on a simplified form of generalized distance in which the variables are assumed to be independent, equivalent to Euclidean distances on standardized measures. Preprocessing - Cluster Analysis Some preprocessing of the input data by the user may be necessary. Any categorical data to be clustered must first be converted to design-coded numeric variables. Since null data values may bias or invalidate the analysis, they may be replaced, or the listwise deletion option selected to exclude rows with any null values in the preprocessing phase. Teradata Warehouse Miner automatically builds a single input table from the requested columns of the requested input table. If the user requests more than 30 input columns, the data is unpivoted with additional rows added for the column values. Through this mechanism, any number of columns within a table may be analyzed, and the SQL optimized for a particular Teradata server capability. Expectation Maximization Algorithm The clustering algorithm requires specification of the desired number of clusters. After preprocessing, an initialization step determines seed values for the clusters, and clustering is then performed based on conditional probability and maximum likelihood principles using the EM algorithm to converge on cluster assignments that yield the maximum likelihood value. In a Gaussian Mixture (GM) model, it is assumed that the variables being modeled are members of a normal (Gaussian) probability distribution. For each cluster, a maximum likelihood equation can be constructed indicating the probability that a randomly selected observation from that cluster would look like a particular observation. A maximum likelihood rule for classification would assign this observation to the cluster with the highest likelihood value. In the computation of these probabilities, conditional probabilities use the relative size of clusters and prior probabilities, to compute a probability of membership of each row to each cluster. Rows are reassigned to clusters with probabilistic weighting, after units of 20 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis distance have been transformed to units of standard deviation of the standard normal distribution via the Gaussian distance function: p mo = 2 –n 2 R –1 2 2 d mo exp – ------------- 2 Where: • p is dimensioned 1 by 1 and is the probability of membership of a point to a cluster • d is dimensioned 1 by 1 and is the Mahalanobis Distance • n is dimensioned 1 by 1 and is the number of variables • R is dimensioned n by n and is the cluster variance/covariance matrix The Gaussian Distance Function translates distance into a probability of membership under this probabilistic model. Intermediate results are saved in Teradata tables after each iteration, so the algorithm may be stopped at any point and the latest results viewed, or a new clustering process begun at this point. These results consist of cluster means, variances and prior probabilities. Expectation Step Means, variances and frequencies of rows assigned by cluster are first calculated. A covariance inverse matrix is then constructed using these variances, with all non-diagonals assumed to be zero. This simplification is tantamount to the assumption that the variables are independent. Performance is improved thereby, allowing the number of calculations to be proportional to the number of variables, rather than its square. Row distances to the mean of each cluster are calculated using a Mahalanobis Distance (MD) metric: n 2 do = o xn – con Rn r –1 x n – c on i = 1j = 1 Where: • m is the number of rows • n is the number of variables • o is the number of clusters • d is dimensioned n by o and is the Mahalanobis Distance from a row to a cluster • x is dimensioned m by n and is the data • c is dimensioned 1 by n and are the cluster centroids • R is dimensioned n by n and is the cluster variance/covariance matrix Mahalanobis Distance is a rescaled unitless data form used to identify outlying data points. Independent variables may be thought of as defining a multidimensional space in which each observation can be plotted. Means (“centroids”) for each independent variable may also be plotted. Mahalanobis distance is the distance of each observation from its centroid, defined by variables that may be dependent. In the special case where variables are independent or uncorrelated, it is equivalent to the simple Euclidean distance. In the default GM model, Teradata Warehouse Miner User Guide - Volume 3 21 Chapter 1: Analytic Algorithms Cluster Analysis separate covariance matrices are maintained, conforming to the specifications of a pure maximum likelihood rule model. The EM algorithm works by performing the expectation and maximization steps iteratively until the log-likelihood value converges (i.e. changes less than a default or specified epsilon value), or until a maximum specified number of iterations has been performed. The loglikelihood value is the sum over all rows of the natural log of the probabilities associated with each cluster assignment. Although the EM algorithm is guaranteed to converge, it is possible it may converge slowly for comparatively random data, or it may converge to a local maximum rather than a global one. Maximization Step The row is assigned to the nearest cluster with a probabilistic weighting for the GM model, or with certainty for the K-Means model. Options - Cluster Analysis K-Means Option With the K-Means option, rows are reassigned to clusters by associating each to the closest cluster centroid using the shortest distance. Data points are assumed to belong to only one cluster, and the determination is considered a ‘hard assignment’. After the distances are computed from a given point to each cluster centroid, the point is assigned to the cluster whose center is nearest to the point. On the next iteration, the point’s value is used to redefine that cluster’s mean and variance. This is in contrast to the default Gaussian option, wherein rows are reassigned to clusters with probabilistic weighting, after units of distance have been transformed to units of standard deviation via the Gaussian distance function. Also with the K-means option, the variables' distances to cluster centroids are calculated by summing, without any consideration of the variances, resulting effectively in the use of unnormalized Euclidean distances. This implies that variables with large variances will have a greater influence over the cluster definition than those with small variances. Therefore, a typical preparatory step to conducting a K-means cluster analysis is to standardize all of the numeric data to be clustered using the Z-score transformation function in Teradata Warehouse Miner. K-means analyses of data that are not standardized typically produce results that: (a) are dominated by variables with large variances, and (b) virtually or totally ignore variables with small variances during cluster formation. Alternatively, the Rescale function could be used to normalize all numeric data, with a lower boundary of zero and an upper boundary of one. Normalizing the data prior to clustering gives all the variables equal weight. Poisson Option The Poisson option is designed to be applied to data containing mixtures of Poissondistributed variables. The data is first normalized so all variables have the same means and variances, allowing the calculation of the distance metric without biasing the result in favor of larger-magnitude variables. The EM algorithm is then applied with a probability metric based on the likelihood function of the Poisson distribution function. As in the Gaussian Mixture Model option, rows are assigned to the nearest cluster with a probabilistic weighting. At the 22 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis end of the EM iteration, the data is unnormalized and saved as a potential result, until or unless replaced by the next iteration. Average Mode - Minimum Generalized Distance Within the GM model, a special “average mode” option is provided, using the minimum generalized distance rule. With this option, a single covariance matrix is used for all clusters, rather than using an individual covariance matrix for each cluster. A weighted average of the covariance matrices is constructed for use in the succeeding iteration. Automatic Scaling of Likelihood Values When a large number of variables are input to the cluster analysis module, likelihood values can become prohibitively small. The algorithm automatically scales these values to avoid loss of precision, without invalidating the results in any way. The expert option ‘Scale Factor Exponent (s)’ may be used to bypass this feature by using a specific value, e.g. 10s, to multiply the probabilities. Continue Option The continue option allows clustering to be resumed where it left off by starting with the cluster centroid, variance and probability values of the last complete iteration saved in the metadata tables. Success Analysis - Cluster Analysis If the log-likelihood value converges, and the requested number of clusters is obtained with significant probabilities, then the clustering analysis may be considered to have been successful. If the log-likelihood value declines, indicating convergence has completed, the iterations stop. On occasion, warning messages may indicate constants within one or more clusters. Using the TWM Cluster Analysis Sampling Large Database Tables as a Starting Method It may be most effective to use the sample parameter to begin the analysis of extremely large databases. The execution times will be much faster, and an approximate result obtained that can be used as a starting point, as described above. Results may be compared using the loglikelihood value, where the largest value indicates the best clustering fit, in terms of maximum likelihood. Since local maxima may result from a particular EM clustering analysis, multiple executions from different samples may produce a seed that ultimately yields the best log-likelihood value. Clustering and Data Problems Common data problems for cluster analysis include insufficient rows provided for the number of clusters requested, and constants in the data resulting in singular covariance matrices. When these problems occur, warning messages and recommendations are provided. An option for dealing with null values during processing is described below. Teradata Warehouse Miner User Guide - Volume 3 23 Chapter 1: Analytic Algorithms Cluster Analysis Additionally, Teradata errors may occur for non-normalized data having more than 15 digits of significance. In this case, a preprocessing step of either multiplying (for small numbers) or dividing (for large numbers) by a constant value may rectify overflow and underflow conditions. The clusters will remain the same as all this does is change the unit of measure. Clustering and Constants in Data When one or more of the variables included in the clustering analysis have only a few values, these values may be singled out and included in particular clusters as constants. This is most likely when the number of clusters sought is large. When this happens, the covariance matrix becomes singular and cannot be inverted, since some of the variances are zero. A feature is provided in the cluster algorithm to improve the chance of success under these conditions, by limiting how close to zero the variance may be set, e.g. 10-3. The default value is 10-10. If the log-likelihood values increase for a number of iterations and then start decreasing, it is likely due to the clustering algorithm having found clusters where selected variables are all the same value (a constant), so the cluster variance is zero. Changing the minimum variance exponent value to a larger value may reduce the effect of these constants, allowing the other variables to converge to a higher log-likelihood value. Clustering and Null Values The presence of null values in the data may result in clusters that differ from those that would have resulted from zero or numeric values. Since null data values may bias or invalidate the analysis, they should be replaced or the column eliminated. Alternatively, the listwise deletion option can be selected to exclude rows with any null values in the preprocessing phase. Optimizing Performance of Clustering Parallel execution of SQL is an important feature of the cluster analysis algorithm in Teradata Warehouse Miner as well as Teradata. The number of variables to cluster in parallel is determined by the ‘width’ parameter. The optimum value of width will depend on the size of the Teradata system, its memory size, and so forth. Experience has shown that when a large number of variables are clustered on, the optimum value of width ranges from 20-25. The width value is dynamically set to the lesser of the specified Width option (default = 25) and the number of columns, but can never exceed 118. If SQL errors indicate insufficient memory, reducing the width parameter may alleviate the problem. Initiate a Cluster Analysis Use the following procedure to initiate a new Cluster analysis in Teradata Warehouse Miner: 24 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis 1 Click on the Add New Analysis icon in the toolbar: Figure 15: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Analytics under Categories and then under Analyses double-click on Clustering: Figure 16: Add New Analysis dialog 3 This will bring up the Clustering dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Cluster - INPUT - Data Selection On the Clustering dialog click on INPUT and then click on data selection: Teradata Warehouse Miner User Guide - Volume 3 25 Chapter 1: Analytic Algorithms Cluster Analysis Figure 17: Clustering > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 Select Columns From a Single Table • Available Databases (or Analyses) — All the databases (or analyses) that are available for the Clustering analysis. • Available Tables — All the tables within the Source Database that are available for the Clustering analysis. • Available Columns — Within the selected table or matrix, all columns which are available for the Clustering analysis. • Selected Columns — Columns must be of numeric type. Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Cluster - INPUT - Analysis Parameters On the Clustering dialog click on INPUT and then click on analysis parameters: Figure 18: Clustering > Input > Analysis Parameters 26 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis On this screen select: • Clustering Algorithm • Gaussian — Cluster the data using a Gaussian Mixture Model as described above. This is the default Algorithm. • Poisson — Cluster the data using a Poisson Mixture Model as described above. • K-Means — Cluster the data using the K-Means Model as described above. • Number of clusters — Enter the number of clusters before executing the cluster analysis. • Convergence Criterion — For the Gaussian and Poisson Mixture Models, clustering is stopped when the log-likelihood increases less than this amount. The default value is 0.001. K-Means, on the other hand, does not use this criterion as clustering stops when the distances of all points to each cluster have not changed from the previous iteration. In other words, when the assignment of rows to clusters has not changed from the previous iteration, clustering has converged. • Maximum Iterations — Clustering is stopped after this maximum number of iterations has occurred. The default value is 50. • Remove Null Values (using Listwise deletion) — This option eliminates all rows from processing that contain any null input columns. The default is enabled. • Include Variable Importance Evaluation reports — Report shows resultant log-likelihood when each variable is successively dropped out of the clustering calculations. The most important variable will be listed next to the most negative log-likelihood value; the least important variable will be listed with the least negative value. • Continue Execution (instead of starting over) — Previous execution results are used as seed values for starting clustering. Cluster - INPUT - Expert Options On the Clustering dialog click on INPUT and then click on expert options: Figure 19: Clustering > Input > Expert Options On this screen select: • Width — Number of variables to process in parallel (dependent on system limits) • Input Sample Fraction — Fraction of input dataset to cluster on. • Scale Factor Exponent — If nonzero “s” is entered, this option overrides automatic scaling, scaling by 10s. • Minimum Probability Exponent — If “e” is entered, the Clustering analysis uses 10e as smallest nonzero number in SQL calculations. Teradata Warehouse Miner User Guide - Volume 3 27 Chapter 1: Analytic Algorithms Cluster Analysis • Minimum Variance Exponent — If “v” is entered, the Clustering analysis uses 10v as the minimum variance in SQL calculations. • Use single cluster covariance — Simplified model that uses the same covariance table for all clusters. • Use Random Seeding — When enabled (default) this option seeds the initial clustering answer matrix by randomly selecting a row for each cluster as the seed. This method is the most commonly used type of seeding for all other clustering systems, according to the literature. The byproduct of using this new method is that slightly different solutions will be provided by successive clustering runs, and convergence may be quicker because fewer iterations may be required. • Seed Sample Percentage — If Use Random Seeding is disabled, the previous seeding method of Teradata Warehouse Miner Clustering, where every row is assigned to one of the clusters, and then averages used as the seeds. Enter a percentage (1-100) of the input dataset to use as the starting seed. Cluster - OUTPUT On the Clustering dialog click on OUTPUT: Figure 20: Cluster > OUTPUT On this screen select: • Store the variables table of this analysis in the database — Check this box to store the variables table of this analysis in two tables in the database, one for cluster columns and one for cluster results. • Database Name — The name of the database to create the output tables in. • Output Table Prefix — The prefix of the output tables. (For example, if test is entered here, tables test_ClusterColumns and test_ClusterResults will be created). • Advertise Output — The Advertise Output option "advertises" output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to the “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. By way of an example, the tutorial example with prefix test yields table test_ ClusterResults: 28 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis Table 4: test_ClusterResults column_ix cluster_id priors m v 1 1 0.0692162138434691 -2231.95933518596 7306685.95957656 1 2 0.403625379654599 -947.132576882845 846532.221977884 1 3 0.527158406501931 -231.599917701351 105775.923364194 2 1 0.0692162138434691 3733.31923440023 18669805.3968291 2 2 0.403625379654599 1293.34863525092 1440668.11504453 2 3 0.527158406501931 231.817911577847 102307.594966697 3 1 0.0692162138434691 3725.87257974281 18930649.6488828 3 2 0.403625379654599 632.603945909026 499736.882919713 3 3 0.527158406501931 163.869611182736 57426.9984808451 and test_ClusterColumns: Table 5: test_ClusterColumns table_name column_name column_alias column_order index_flag variable_type twm_ customer_ analysis avg_cc_bal avg_cc_bal 1 0 1 twm_ customer_ analysis avg_ck_bal avg_ck_bal 2 0 1 twm_ customer_ analysis avg_sv_bal avg_sv_bal 3 0 1 If Database Name is twm_results and Output Table Prefix is test, these tables are defined respectively as: CREATE SET TABLE twm_results.test_ClusterResults ( column_ix INTEGER, cluster_id INTEGER, priors FLOAT, m FLOAT, v FLOAT) UNIQUE PRIMARY INDEX ( column_ix ,cluster_id ); CREATE SET TABLE twm_results.test_ClusterColumns ( table_name VARCHAR(30) CHARACTER SET UNICODE NOT CASESPECIFIC, column_name VARCHAR(30) CHARACTER SET UNICODE NOT CASESPECIFIC, Teradata Warehouse Miner User Guide - Volume 3 29 Chapter 1: Analytic Algorithms Cluster Analysis column_alias VARCHAR(100) CHARACTER SET UNICODE NOT CASESPECIFIC, column_order SMALLINT, index_flag SMALLINT, variable_type INTEGER) UNIQUE PRIMARY INDEX ( table_name ,column_name ); Run the Cluster Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Cluster Analysis The results of running the Cluster analysis include a variety of statistical reports, a similarity/ dissimilarity graph, as well as a cluster size and distance measure graph. All of these results are outlined below. Cluster - RESULTS - reports On the Clustering dialog click on RESULTS and then click on reports: Figure 21: Clustering > Results > Reports Clustering Progress • Iteration — This represents the number of the step in the Expectation Maximization clustering algorithm as it seeks to converge on a solution maximizing the log likelihood function. • Log Likelihood — This is the log likelihood value calculated at the end of this step in the Expectation Maximization clustering algorithm. It does not appear when the K-Means option is used. • Diff — This is simply the difference in the log likelihood value between this and the previous step in the modeling process, starting with 0 at the end of the first step. It does not appear when the K-Means option is used. • Timestamp — This is the day, date, hour, minute and second marking the end of this step in processing. 30 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis Importance of Variables This report is available when the Include Variable Importance Evaluation Report option is enabled on the Expert Options tab. • Col — The column number in the order the input columns were requested. • Name — Name of the column being clustered. • Log Likelihood — This is the log likelihood value calculated if this variable was removed from the clustering solution. Clustering Solution • Col — This is the column number in the order the input columns were requested. • Table_Name — The name of the table associated with this input column. • Column_Name — The name of the input column used in performing the cluster analysis. • Cluster_Id — The cluster number that this data applies to, from 1 to the number of clusters requested. • Weight — This is the so-called “prior probability” that an observation would belong to this cluster, based on the percentage of observations belonging to this cluster at this stage. • Mean — When the Gaussian Mixture Model algorithm is selected, Mean is the weighted average of this column or variable amongst all the observations, where the weight used is the probability of inclusion in this cluster. When the K-Means algorithm is selected, Mean is the average value of this column or variable amongst the observations assigned to this cluster at this iteration of the algorithm. • Variance — When the Gaussian Mixture Model algorithm is selected, Variance is the weighted variance of this variable amongst all the observations, where the weight used is the probability of inclusion in this cluster. When the K-Means algorithm is selected, Variance is the variance of this variable amongst the observations assigned to this cluster at this iteration. (Variance is the square of a variable’s standard deviation, measuring in some sense how its value varies from one observation to the next). Cluster - RESULTS - sizes graph On the Clustering dialog click on RESULTS and then click on sizes graph: Figure 22: Clustering > Results > Sizes Graph The Sizes (and Distances) graph plots the mean values of a pair of variables at a time, indicating the clusters by color and number label, and the standard deviations (square root of the variance) by the size of the ellipse surrounding the mean point, using the same colorcoding. Roughly speaking, this graph depicts the separation of the clusters with respect to pairs of model variables. The following options are available: Teradata Warehouse Miner User Guide - Volume 3 31 Chapter 1: Analytic Algorithms Cluster Analysis • Non-Normalized — The default value to show the clusters without any normalization. • Normalized — With the Normalized option, cluster means are divided by the largest absolute mean and the size of the circle based on the variance is divided by the largest absolute variance. • Variables • Available — The variables that were input into the Clustering Analysis. • Selected — The variables that will be shown on the Size and Distances graph. Two variables are required to be entered here. • Clusters • Available — A list of clusters generated in the clustering solution. • Selected — The clusters that will be shown on the Size and Distances graph. Up to twelve clusters can be selected to be shown on the Size and Distances graph. • Zoom In — While holding down the left mouse button on the Size and Distances graph, drag a lasso around the area that you desire to magnify. Release the mouse button for the zoom to take place. This can be repeated until the desired level of magnification is achieved. • Zoom Out — Hit the “Z” key, or toggle the Graph Options tab to go back to the original magnification level. Cluster - RESULTS - similarity graph On the Clustering dialog click on RESULTS and then click on similarity graph: Figure 23: Clustering > Results > Similarity Graph The Similarity graph allows plotting the means and variances of up to twelve clusters and twelve variables at one time. The cluster means, i.e. the mean values of the variables for the data points assigned to the cluster, are displayed with values varying along the x-axis. A different line parallel to the x-axis is used for each variable. The normalized variances are displayed for each variable by color-coding, and the clusters are identified by number next to the point graphed. Roughly speaking, the more spread out the points on the graph, the more differentiated the clusters are. The following options are available: • Non-Normalized — The default value to show the clusters without any normalization. • Normalized — With the Normalized option, the cluster mean is divided by the largest absolute mean. • Variables • 32 Available — The variables that were input into the Clustering Analysis. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis • Selected — The variables that will be shown on the Similarity graph. Up to twelve variables can be entered here. selected to be shown on the Similarity graph • Clusters • Available — A list of clusters generated in the clustering solution. • Selected — The clusters that will be shown on the Similarity graph. Up to twelve clusters can be selected to be shown on the Similarity graph. Tutorial - Cluster Analysis In this example, Gaussian Mixture Model cluster analysis is performed on 3 variables giving the average credit, checking and savings balances of customers, yielding a requested 3 clusters. Note that since Clustering in Teradata Warehouse Miner is non-deterministic, the results may vary from these, or from execution to execution. Parameterize a Cluster analysis as follows: • Selected Tables and Columns • twm_customer_analysis.avg_cc_bal • twm_customer_analysis.avg_ck_bal • twm_customer_analysis.avg_sv_bal • Number of Clusters — 3 • Algorithm — Gaussian Mixture Model • Convergence Criterion — 0.1 • Use Listwise deletion to eliminate null values — Enabled Run the analysis and click on Results when it completes. For this example, the Clustering Analysis generated the following pages. Note that since Clustering is non-deterministic, results may vary. A single click on each page name populates the page with the item. Table 6: Progress Iteration Log Likelihood Diff Timestamp 1 -25.63 0 3:05 PM 2 -25.17 .46 3:05 PM 3 -24.89 .27 3:05 PM 4 -24.67 .21 3:05 PM 5 -24.42 .24 3:05 PM 6 -24.33 .09 3:06 PM Teradata Warehouse Miner User Guide - Volume 3 33 Chapter 1: Analytic Algorithms Cluster Analysis Table 7: Solution Col Table_Name Column_Name Cluster_Id Weight Mean Variance 1 twm_customer_analysis avg_cc_bal 1 .175 -1935.576 3535133.504 2 twm_customer_analysis avg_ck_bal 1 .175 2196.395 9698027.496 3 twm_customer_analysis avg_sv_bal 1 .175 674.72 825983.51 1 twm_customer_analysis avg_cc_bal 2 .125 -746.095 770621.296 2 twm_customer_analysis avg_ck_bal 2 .125 948.943 1984536.299 3 twm_customer_analysis avg_sv_bal 2 .125 2793.892 11219857.457 1 twm_customer_analysis avg_cc_bal 3 .699 -323.418 175890.376 2 twm_customer_analysis avg_ck_bal 3 .699 570.259 661100.56 3 twm_customer_analysis avg_sv_bal 3 .699 187.507 63863.503 Sizes Graph By default, the following graph will be displayed. This parameterization includes: • Non-Normalized — Enabled • Variables Selected • avg_cc_bal • avg_ck_bal • Clusters Selected 34 • Cluster 1 • Cluster 2 • Cluster 3 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Cluster Analysis Figure 24: Clustering Analysis Tutorial: Sizes Graph Similarity Graph By default, the following graph will be displayed. This parameterization includes: • Non-Normalized — Enabled • Variables Selected • avg_cc_bal • avg_ck_bal • avg_sv_bal • Clusters Selected • Cluster 1 • Cluster 2 • Cluster 3 Teradata Warehouse Miner User Guide - Volume 3 35 Chapter 1: Analytic Algorithms Decision Trees Figure 25: Clustering Analysis Tutorial: Similarity Graph Decision Trees Overview Decision tree models are most commonly used for classification. What is a classification model or classifier? It is simply a model for predicting a categorical variable, that is a variable that assumes one of a predetermined set of values. These values can be either nominal or ordinal, though ordinal variables are typically treated the same as nominal ones in these models. (An example of a nominal variable is single, married and divorced marital status, while an example of an ordinal or ordered variable is low, medium and high temperature). It is the ability of decision trees to not only predict the value of a categorical variable, but to directly use categorical variables as input or predictor variables that is perhaps their principal advantage. Decision trees are by their very nature also well suited to deal with large numbers of input variables, handle a mixture of data types and handle data that is not homogeneous, i.e. the variables do not have the same interrelationships throughout the data space. They also provide insight into the structure of the data space and the meaning of a model, a result at times as important as the accuracy of a model. It should be noted that a variation of decision trees called regression trees can be used to build regression models rather than classification models, enjoying the same benefits just described. Most of the upcoming discussion is geared toward classification trees with regression trees described separately. What are Decision Trees? What does a decision tree model look like? It first of all has a root node, which is associated with all of the data in the training set used to build the tree. Each node in the tree is either a decision node or a leaf node, which has no further connected nodes. A decision node 36 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees represents a split in the data based on the values of a single input or predictor variable. A leaf node represents a subset of the data that has a particular value of the predicted variable, i.e. the resulting class of the predicted variable. A measure of accuracy is also associated with the leaf nodes of the tree. The first issue in building a tree is the decision as to how data should be split at each decision node in the tree. The second issue is when to stop splitting each decision node and make it a leaf. And finally, what class should be assigned to each leaf node. In practice, researchers have found that it is usually best to let a tree grow as big as it needs to and then prune it back at the end to reduce its complexity and increase its interpretability. Once a decision tree model is built it can be used to score or classify new data. If the new data includes the values of the predicted variable it can be used to measure the effectiveness of the model. Typically though scoring is performed in order to create a new table containing key fields and the predicted value or class identifier. Decision Trees in Teradata Warehouse Miner Teradata Warehouse Miner provides decision trees for classification models and regression models. They are built largely on the techniques described in [Breiman, Friedman, Olshen and Stone] and [Quinlan]. As such, splits using the Gini diversity index, regression or information gain ratio are provided. Pruning is also provided, using either the Gini diversity index or gain ratio technique. In addition to a summary report, a graphical tree browser is provided when a model is built, displaying the model either as a tree or a set of rules. Finally, a scoring function is provided to score and/or evaluate a decision tree model. The scoring function can also be used to simply generate the scoring SQL for later use. A number of additional options are provided when building or scoring a decision tree model. One of these options is whether or not to bin numeric variables during the tree building process. Another involves including recalculated confidence measures at each leaf node in a tree based on a validation table, supplementing confidence measures based on the training data used to build the tree. Finally, at the time of scoring, a table profiling the leaf nodes in the tree can be requested, at the same time each scored row is linked with a leaf node and corresponding rule set. Decision Tree SQL Generation A key part to the design of the Teradata Warehouse Miner Decision Trees is SQL generation. In order to avoid having to extract all of the data from the RDBMS, the product generates SQL statements to return sufficient statistics. Before the model building begins, SQL is generated to give a better understanding of the attributes and the predicted variable. For each attribute, the algorithm must determine its cardinality and get all possible values of the predicted variable and the counts associated with it from all of the observations. This information helps to initialize some structures in memory for later use in the building process. The driving SQL behind the entire building process is a SQL statement that makes it possible to build a contingency table from the data. A contingency table is an m x n matrix that has m rows corresponding to the distinct values of an attribute by n columns that correspond to the predicted variable’s distinct values. The Teradata Warehouse Miner Decision Tree algorithms can quickly generate the contingency table on massive amounts of data rows and columns. Teradata Warehouse Miner User Guide - Volume 3 37 Chapter 1: Analytic Algorithms Decision Trees This contingency table query allows the program to gather the sufficient statistics needed for the algorithms to do their calculations. Since this consists of the counts of the N distinct values of the dependent variable, a WHERE clause is simply added to this SQL when building a contingency table on a subset of the data instead of the data in the whole table. The WHERE clause expression in the statement helps define the subset of data which is the path down the tree that defines which node is a candidate to be split. Each type of decision tree uses a different method to compute which attribute is the best choice to split a given subset of data upon. Each type of decision tree is considered in turn in what follows. In the course of describing each algorithm, the following notation is used: 1 t denotes a node 2 j denotes the learning classes 3 J denotes the number of classes 4 s denotes a split 5 N(t) denotes the number of cases within a node t 6 p(j|t) is the proportion of class j learning samples in node t 7 An impurity function is a symmetric function with maximum value –1 –1 –1 J J J and 1 0 0 = 0 1 0 = = 0 0 1 = 0 8 t1 denotes a subnode i of t 9 i(t) denotes node impurity measure 10 t1 and tR are the left and right split nodes of t Splitting on Information Gain Ratio Information theory is the basic underlying idea in this type of decision tree. Splits on categorical variables are made on each individual value. Splits on continuous variables are made at one point in an ordered list of the actual values, that is a binary split is introduced right on a particular value. • Define the “info” at node t as the entropy: info t = – p j t log 2 p j t • Suppose t is split into subnodes t1, …, t2 by predictor X. Define: Info x = N t1 info t1 -----------Nt Gain X = info t – info x t N t1 N t1 Split info X = – ------------- log 2 ------------- Nt Nt 38 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees gain X Gain ratio X = ------------------------------------Split info X Once the gain ratios have been computed the attribute with the highest gain ratio is used to split the data. Then each subset goes through this process until the observations are all of one class or a stopping criterion is met such as each node must contain at least 2 observations. For a detailed description of this type of decision tree see [Quinlan]. Splitting on Gini Diversity Index Node impurity is the idea behind the Gini diversity index split selection. To measure node impurity, use the formula: i t = p t 0 Maximum impurity arises when there is an equal distribution of the class that is to be predicted. As in the heads and tails example, impurity is highest if half the total is heads and the other half is tails. On the other hand, if there were only tails in a certain sample the impurity would be 0. The Gini index uses the following formula for its calculation of impurity: it = 1 – p j t 2 j For a determination of the goodness of a split, the following formula is used: i s t = i t – p L i t L – p R i t R where tL and tR are the left and right sub nodes of t and pL and pR are the probabilities of being in those sub nodes. For a detailed description of this type of tree see [Breiman, Friedman, Olshen and Stone]. Regression Trees Teradata Warehouse Miner provides regression tree models that are built largely on the techniques described in [Breiman, Friedman, Olshen and Stone]. Like classification trees, regression trees utilize SQL in order to extract only the necessary information from the RDBMS instead of extracting all the data from the table. An m x 3 table is returned from the database that has m rows corresponding to the distinct values of an attribute followed by the SUM and SQUARED SUM of the predicted variable and the total number of rows having that attribute value. Using the formula: yn – avg(y) Teradata Warehouse Miner User Guide - Volume 3 2 39 Chapter 1: Analytic Algorithms Decision Trees the sum of squares for any particular node starting with the root node of all the data is calculated first. The regression tree is built by iteratively splitting nodes and picking the split for that node which will maximize a decrease in the within node sum of squares of the tree. Splitting stops if the minimum number of observations in a node is reached or if all of the predicted variable values are the same. The value to predict for a leaf node is simply the average of all the predicted values that fall into that leaf during model building. Chaid Trees CHAID trees utilize the chi squared significance test as a means of partitioning data. Independent variables are tested by looping through the values and merging categories that have the least significant difference from one another and also are still below the merging significance level parameter (default .05). Once all independent variables have been optimally merged the one with the highest significance is chosen for the split, the data is subdivided, and the process is repeated on the subsets of the data. The splitting stops when the significance goes above the splitting significance level (default .05). For a detailed description of this type of tree see [Kass]. Decision Tree Pruning Many times with algorithms such as those described above, a model over fits the data. One of the ways of correcting this is to prune the model from the leaves up. In situations where the error rate of leaves doesn’t increase when combined then they are joined into a new leaf. A simple example may be given as follows. If there is nothing but random data for the attributes and the class is set to predict “heads” 75% of the time and “tails” 25% of the time, the result will be an over fit model that doesn’t predict the outcome well. Just by looking it can be seen that instead of a built up model with many leaves, the model could just predict “heads” and it would be correct 75% of the time, whereas over fitting usually does much worse in such a case. Teradata Warehouse Miner provides pruning according to the gain ratio and Gini diversity index pruning techniques. It is possible to combine different splitting and pruning techniques, however when pruning a regression tree the Gini diversity index technique must be used. Decision Trees and NULL Values NULL values are handled by listwise deletion. This means that if there are NULL values in any variables (independent and dependent) then that row where a NULL exists will be removed from the model building process. NULL values in scoring, however, are handled differently. Unlike in tree building where listwise deletion is used, scoring can sometimes handle rows that have NULL values in some of the independent variables. The only time a row will not get scored is if a decision node that the row is being tested on has a NULL value for that decision. For instance, if the first split in a tree is “age < 50,” only rows that don’t have a NULL value for age will pass down further in the tree. This row could have a NULL value in the income variable. But since this decision is on age, the NULL will have no impact at this split and the row will continue down the 40 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees branches until a leaf is reached or it has a NULL value in a variable used in another decision node. Initiate a Decision Tree Analysis Use the following procedure to initiate a new Decision Tree analysis in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 26: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Analytics under Categories and then under Analyses double-click on Decision Tree: Figure 27: Add New Analysis dialog 3 This will bring up the Decision Tree dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Decision Tree - INPUT - Data Selection On the Decision Tree dialog click on INPUT and then click on data selection: Teradata Warehouse Miner User Guide - Volume 3 41 Chapter 1: Analytic Algorithms Decision Trees Figure 28: Decision Tree > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 Select Columns From a Single Table • Available Databases (or Analyses) — All the databases (or analyses) that are available for the Decision Tree analysis. • Available Tables — All the tables that are available for the Decision Tree analysis. • Available Columns — Within the selected table or matrix, all columns that are available for the Decision Tree analysis. • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can either insert columns as Dependent or Independent columns. Make sure you have the correct portion of the window highlighted. 42 • Independent — These may be of numeric or character type. • Dependent — The dependent variable column is the column whose value is being predicted. It is selected from the Available Variables in the selected table. When Gain Ratio or Gini Index are selected as the Tree Splitting criteria, this is treated as a categorical variable with distinct values, in keeping with the nature of classification trees. Note that in this case an error will occur if the Dependent Variable has more than 50 distinct values. When Regression Trees is selected as the Tree Splitting criteria, this is treated as a continuous variable. In this case it must contain only numeric values. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees Decision Tree - INPUT - Analysis Parameters On the Decision Tree dialog click on INPUT and then click on analysis parameters: Figure 29: Decision Tree > Input > Analysis Parameters On this screen select: • Splitting Options • Splitting Method • Gain Ratio — Option to use the Gain Ratio splitting criteria. • Gini Index — Option to use the Gini Index splitting criteria. • Chaid — Option to use the Chaid splitting criteria. When using this option you are also given the opportunity to change the merging or splitting Chaid Significance Levels. • Regression Trees — Option to use the Regression splitting criteria as outlined above. • Minimum Split Count — This option determines how far the splitting of the decision tree will go. Unless a node is pure (meaning it has only observations with the same dependent value) it will split if each branch that can come off this node will contain at least this many observations. The default is a minimum of 2 cases for each branch. • Maximum Nodes — If the nodes in the tree are equal to or exceed this value while splitting a certain level of the tree, the algorithm stops the tree growing after completing this level and returns the tree built so far. The default is 10000 nodes. • Maximum Depth — Another method of stopping the tree is to specify the maximum depth the tree may grow to. This option will stop the algorithm if the tree being built has this many levels. The default is 100 levels. • Chaid Significance Levels • • Merging — Independent variables are tested by looping through the values and merging categories that have the least significant difference from one another and also are still below this merging significance level parameter (default .05). • Splitting — Once all independent variables have been optimally merged the one with the highest significance is chosen for the split, the data is subdivided, and the process is repeated on the subsets of the data. The splitting stops when the significance goes above this splitting significance level parameter (default .05). Bin Numeric Variables — Option to automatically Bincode the continuous independent variables. Continuous data is separated into one hundred bins when this option is selected. If the variable has less than one hundred distinct values, this option is ignored. Teradata Warehouse Miner User Guide - Volume 3 43 Chapter 1: Analytic Algorithms Decision Trees • • Include Validation Table — A supplementary table may be utilized in the modeling process to validate the effectiveness of the model on a separate set of observations. If specified, this table is used to calculate a second set of confidence or targeted confidence factors. These recalculated confidence factors may be viewed in the tree browser and/or added to the scored table when scoring the resultant model. When Include Validation Table is selected, a separate validation table is required. • Database — The name of the database to look in for the validation table - by default, this is the source database. • Table — The name of the validation table to use for recalculating confidence or targeted confidence factors. Include Lift Table — Option to generate a Cumulative Lift Table in the report to demonstrates how effective the model is in estimating the dependent variable. Valid for binary dependent variables only. • Response Value — An optional response value can be specified for the dependent variable that will represent the response value. Note that all other dependent variable values will be considered a non-response value. Values — Bring up the Decision Tree values wizard to help in specifying the response value. • Pruning Options • • Pruning Method — Pull-down list with the following values: • Gain Ratio — Option to use the Gain Ratio pruning criteria as outlined above. • Gini Index — Option to use the Gini Index pruning criteria as outlined above. • None — Option to not prune the resultant decision tree. Gini Test Table — When Gini Index pruning is selected as the pruning method, a separate Test table is required. • Database — The name of the database to look for the Test table - by default, this is the source database. • Table — The name of the table to use for test purposes during the Gini Pruning process. Decision Tree - INPUT - Expert Options On the Decision Tree dialog click on INPUT and then click on expert options: Figure 30: Decision Tree > Input > Expert Options • Performance 44 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees • Maximum amount of data for in-memory processing — By default, 2 MB of data can be processed in memory for the tree. This can be increased here. For smaller data sets, this option may be preferable over the SQL version of the decision tree. Run the Decision Tree Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Decision Tree The results of running the Decision Tree analysis include a variety of statistical reports as well as a Graphic and Textual Tree browser. All of these results are outlined below. Decision Tree Reports • Total observations — This is the number of observations in the training data set used to build the tree. More precisely, this is the number of rows in the input table after any rows have been excluded for containing a null value in a column selected as an independent or dependent variable. • Nodes before pruning — This is the number of nodes in the tree, including the root node, before it is pruned back in the second stage of the tree-building process. • Nodes after pruning — This is the number of nodes in the tree, including the root node, after it is pruned back in the second stage of the tree-building process. • Total nodes — This is the number of nodes in the tree, including the root node, when either pruning is not requested or doesn’t remove any nodes. • Model Accuracy — This is the percentage of observations in the training data set that the tree accurately predicts the value of the dependent variable for. Variables • Independent Variables — A list of all the independent variables that made it into the decision tree model. • Dependent Variable — The dependent variable that the tree was built to predict. Confusion Matrix A N x (N+2) (for N outcomes of the dependent variable) confusion matrix is given with the following format: Teradata Warehouse Miner User Guide - Volume 3 45 Chapter 1: Analytic Algorithms Decision Trees Table 8: Confusion Matrix Format Actual ‘0’ Actual ‘1’ … Actual ‘N’ Correct Incorrect Predicted ‘0’ # correct ‘0’ Predictions # incorrect‘1’ Predictions … # incorrect ‘N’ Predictions Total Correct ‘0’ Predictions Total Incorrect ‘0’ Predictions Predicted ‘1’ # incorrect‘0’ Predictions # correct ‘1’ Predictions … # incorrect ‘N’ Predictions Total Correct ‘1’ Predictions Total Incorrect ‘1’ Predictions … … … … … … … Predicted ‘N’ # incorrect‘0’ Predictions # incorrect ‘1’ Predictions … # correct ‘N’ Predictions Total Correct ‘N’ Predictions Total Incorrect ‘N’ Predictions Validation Matrix When the Include validation table option is selected, a validation matrix similar to the confusion matrix is produced based on the data in the validation table rather than the input table. Cumulative Lift Table The Cumulative Lift Table demonstrates how effective the model is in estimating the dependent variable. It is produced using deciles based on the probability values. Note that the deciles are labeled such that 1 is the highest decile and 10 is the lowest, based on the probability values calculated by logistic regression. The information in this report however is best viewed in the Lift Chart produced as a graph. Note that this is only valid for binary dependent variables. • Decile — The deciles in the report are based on the probability values predicted by the model. Note that 1 is the highest decile and 10 is the lowest. That is, decile 1 contains data on the 10% of the observations with the highest estimated probabilities that the dependent variable is 1. • Count — This column contains the count of observations in the decile. • Response — This column contains the count of observations in the decile where the actual value of the dependent variable is 1. • Pct Response — This column contains the percentage of observations in the decile where the actual value of the dependent variable is 1. • Pct Captured Response — This column contains the percentage of responses in the decile over all the responses in any decile. • Lift — The lift value is the percentage response in the decile (Pct Response) divided by the expected response, where the expected response is the percentage of response or dependent 1-values over all observations. For example, if 10% of the observations overall have a dependent variable with value 1, and 20% of the observations in decile 1 have a dependent variable with value 1, then the lift value within decile 1 is 2.0, meaning that the model gives a “lift” that is better than chance alone by a factor of two in predicting response values of 1 within this decile. 46 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees • Cumulative Response — This is a cumulative measure of Response, from decile 1 to this decile. • Cumulative Pct Response — This is a cumulative measure of Pct Response, from decile 1 to this decile. • Cumulative Pct Captured Response — This is a cumulative measure of Pct Captured Response, from decile 1 to this decile. • Cumulative Lift — This is a cumulative measure of Lift, from decile 1 to this decile. Decision Tree Graphs The Decision Tree Analysis can display either a graphical and textual representation of the decision tree model, as well as a lift chart. Options are available to display decisions for any node in the graphical or textual tree, as well as the counts and distribution of the dependent variable. Additionally, manual pruning of the decision tree model is supported. Tree Browser Figure 31: Tree Browser When Tree Browser is selected, two frames are shown: the upper frame gives a condensed view to aid in navigating through the detailed tree in the lower frame. Set options by rightclicking on either frame to select from the following menu: • Small Navigation Tree — Under Small Navigation Tree, the options are: Teradata Warehouse Miner User Guide - Volume 3 47 Chapter 1: Analytic Algorithms Decision Trees Figure 32: Tree Browser menu: Small Navigation Tree • Zoom — This option allows you to scale down the navigation tree so that more of it will appear within the window. A slider bar is provided so you can select from a range of new sizes while previewing the effect on the navigation tree. The slider bar can also be used to bring the navigation tree back up to a larger dimension after it has been reduced in size: Figure 33: Tree Browser menu: Zoom Tree • Show Extents Box/Hide Extents Box — With this option a box is drawn around the nodes in the upper frame corresponding to the nodes displayed in the lower frame. The box can be dragged and dropped over segments of the small tree, automatically positioning the identical area in the detailed tree within the lower frame. Once set, the option changes to allow hiding the box. • Hide Navigation Tree/Show Navigation Tree — With this option the upper frame is made to disappear (or reappear) in order to give more room to the lower frame that contains the details of the tree. • Show Confidence Factors/Show Targeted Confidence — The Confidence Factor is a measure of how “confident” the model is that it can predict the correct score for a record that falls into a particular leaf node based on the training data the model was built from. For example, if a leaf node contained 10 observations and 9 of them predict Buy and the other record predicts Do Not Buy, then the model built will have a confidence factor of .9, or 90% sure of predicting the right value for a record that falls into that leaf node of the model. Models built with a predicted variable that has only 2 outcomes can display a Targeted Confidence value rather than a confidence factor. If the outcomes were 9 Buys and 1 Do Not Buy at a particular node and if the target value was set to Buy, .9 is the targeted 48 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees confidence. However if it is desired to target the Do Not Buy outcome by setting the value to Do Not Buy, then any record falling into this leaf of the tree would get a targeted confidence of .1 or 10%. This option also controls whether Recalculated Confidence Factors or Recalculated Targeted Confidence factors are displayed in the case when the Include validation table option is selected. • Node Detail — The Node Detail feature can be used to copy the entire rule set for a particular node to the Windows Clipboard for use in other applications. • Print Figure 34: Tree Browser menu: Print • Large Tree — Allows you to print the entire tree diagram. This will be printed in pages, with the total number of pages reported before they are printed. (A page will also be printed showing how the tree was mapped into individual pages). If All Pages is selected the entire tree will be printed, across multiple pages if necessary. If Current Browser Page is selected then only that portion of the tree which is viewable will be printed in WYSIWYG fashion. • Small Tree — The entire navigation tree, showing the overall structure of the tree diagram without node labels or statistics, can be printed in pages. (The fewest possible pages will be printed if the navigation tree is reduced as small as possible before printing the small tree). The total number of pages needed to print the smaller tree will be reported before they are sent to the printer). • Save — Currently, the Tree Browser only supports the creation of Bitmaps. If Tree Text is currently selected, the entire tree will be saved. If Tree Browser is selected, only the portion of the tree that is viewable will be saved in WYSIWYG fashion. The lower frame shows the details of the decision tree in a graphical manner. The graphical representation of the tree consists of the following objects: • Root Node — The box at the top of the tree shows the total number of observations or rows used in building the tree after any rows have been removed for containing null values. • Intermediate Node — The boxes representing intermediate nodes in the tree contain the following information. • Decision — Condition under which data passes through this node. • N — Count of number of observations or rows passing through this node. • % — Percentage of observations or rows passing through this node. • Leaf Node — The boxes representing leaf nodes in the tree contain the following information. Teradata Warehouse Miner User Guide - Volume 3 49 Chapter 1: Analytic Algorithms Decision Trees • Decision — Condition under which data passes to this node. • N — Count of number of observations or rows passing to this node. • % — Percentage of observations or rows passing to this node. • CF — Confidence factor • TF — Targeted confidence factor, alternative to CF display • RCF — Recalculated confidence factor based on validation table (if requested) • RTF — Recalculated targeted confidence factor based on validation table (if requested) Text Tree When Tree Text is selected, the diagram represents the decisions made by the tree as a hierarchical structure of rules as follows: Figure 35: Text Tree The first rule corresponds to the root node of the tree. The rules corresponding to leaves in the tree are distinguished by an arrow drawn as ‘-->’, followed by a predicted value of the dependent variable. Rules List On both the Tree Browser and Text Tree, passing the mouse over a node or rule results in a hyperlink indication. When Rules List is enabled, clicking on the hyperlink results in a popup displaying all rules leading to that node or decision as follows: 50 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees Figure 36: Rules List Note that the Node Detail, as described above, can be used to copy the Rules List to the Windows Clipboard. Counts and Distributions On both the Tree Browser and Text Tree, passing the mouse over a node or rule results in a hyperlink indication. When Counts and Distributions is enabled, clicking on the hyperlink results in a pop-up displaying the Count/Distribution of the dependent variable at that node as follows. Note that the Counts and Distribution option is only enabled when the dependent variable is multinomial. For regression trees this is not valid, and it is shown directly on the node or rule for binary trees. Figure 37: Counts and Distributions Note that the Node Detail, as described above, can be used to copy the Counts and Distribution list to the Windows Clipboard. Teradata Warehouse Miner User Guide - Volume 3 51 Chapter 1: Analytic Algorithms Decision Trees Tree Pruning On both the Tree Browser and Text Tree, passing the mouse over a node or rule results in a hyperlink indication. When Tree Pruning is enabled, the following menu appears: Figure 38: Tree Pruning menu Clicking on a node or rule highlights the node and all subnodes, indicating which portion of the tree will be pruned. Additionally, the Prune Selected Branch option becomes enabled as follows: Figure 39: Tree Pruning Menu > Prune Selected Branch Clicking on Prune Selected Branch will convert the highlighted node to a leaf node, and all subnode will disappear. When this is done, the other two Tree Pruning options become enabled: Figure 40: Tree Pruning menu (All Options Enabled) Click on Undo Last Prune, to revert back to the original tree, or the previously pruned tree if Prune Selected Branch was done multiple times. Click on Save Pruned Tree to save the tree to XML. This will be saved in metadata and can be rescored in a future release. 52 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees After a tree is manually pruned and saved to metadata using the Save Pruned Tree option, it can be reopened and viewed in the Tree Browser and, if desired, pruned further. (All additional prunes must be re-saved to metadata). A previously pruned tree will be labeled to distinguish it from a tree that has not been manually pruned: Figure 41: Decision Tree Graph: Previously Pruned Tree “More >>” On both the Tree Browser and Text Tree, if Gini Index has been selected for Tree Splitting, large surrogate splits may occur. If a surrogate split is proceeded by “more >>”, the entire surrogate split can be displayed in a separate pop-up screen by clicking on the node and/or rule as follows: Figure 42: Decision Tree Graph: Predicate Lift Chart This graph displays the statistic in the Cumulative Lift Table, with the following options: • Non-Cumulative • % Response — This column contains the percentage of observations in the decile where the actual value of the dependent variable is 1. • % Captured Response — This column contains the percentage of responses in the decile over all the responses in any decile. • Lift — The lift value is the percentage response in the decile (Pct Response) divided by the expected response, where the expected response is the percentage of response or dependent 1-values over all observations. For example, if 10% of the observations overall have a dependent variable with value 1, and 20% of the observations in decile 1 have a dependent variable with value 1, then the lift value within decile 1 is 2.0, meaning that the model gives a “lift” that is better than chance alone by a factor of two in predicting response values of 1 within this decile. • Cumulative Teradata Warehouse Miner User Guide - Volume 3 53 Chapter 1: Analytic Algorithms Decision Trees • % Response — This is a cumulative measure of the percentage of observations in the decile where the actual value of the dependent variable is 1, from decile 1 to this decile. • % Captured Response — This is a cumulative measure of the percentage of responses in the decile over all the responses in any decile, from decile 1 to this decile. • Cumulative Lift — This is a cumulative measure of the percentage response in the decile (Pct Response) divided by the expected response, where the expected response is the percentage of response or dependent 1-values over all observations, from decile 1 to this decile. Any combination of options can be displayed as follows: Figure 43: Decision Tree Graph: Lift Tutorial - Decision Tree In this example a standard Gain Ratio tree was built to predict credit card ownership ccacct based on 20 numeric and categorical input variables. Notice that the tree initially built contained 100 nodes but was pruned back to only 11, counting the root node. This yielded not only a relatively simple tree structure, but also Model Accuracy of 95.72% on this training data. Parameterize a Decision Tree as follows: • Available Tables — twm_customer_analysis • Dependent Variable — ccacct • Independent Variables 54 • income • age • years_with_bank Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees • nbr_children • gender • marital_status • city_name • state_code • female • single • married • separated • ckacct • svacct • avg_ck_bal • avg_sv_bal • avg_ck_tran_amt • avg_ck_tran_cnt • avg_sv_tran_amt • avg_sv_tran_cnt • Tree Splitting — Gain Ratio • Minimum Split Count — 2 • Maximum Nodes — 1000 • Maximum Depth — 10 • Bin Numeric Variables — Disabled • Pruning Method — Gain Ratio • Include Lift Table — Enabled • Response Value — 1 Run the analysis and click on Results when it completes. For this example, the Decision Tree Analysis generated the following pages. A single click on each page name populates the page with the item. Table 9: Decision Tree Report Total observations 747 Nodes before pruning 33 Nodes after pruning 11 Model Accuracy 95.72% Teradata Warehouse Miner User Guide - Volume 3 55 Chapter 1: Analytic Algorithms Decision Trees Table 10: Variables: Dependent Dependent Variable ccacct Table 11: Variables: Independent Independent Variables income ckacct avg_sv_bal avg_sv_tran_cnt Table 12: Confusion Matrix Actual Non-Response Actual Response Correct Incorrect Predicted 0 340 / 45.52% 0 / 0.00% 340 / 45.52% 0 / 0.00% Predicted 1 32 / 4.28% 375 / 50.20% 375 / 50.20% 32 / 4.28% Table 13: Cumulative Lift Table Cumulative Response Cumulative Response (%) Cumulative Captured Response (%) Cumulative Lift Decile Count Response Response (%) Captured Response (%) 1 5.00 5.00 100.00 1.33 1.99 5.00 100.00 1.33 1.99 2 0.00 0.00 0.00 0.00 0.00 5.00 100.00 1.33 1.99 3 0.00 0.00 0.00 0.00 0.00 5.00 100.00 1.33 1.99 4 0.00 0.00 0.00 0.00 0.00 5.00 100.00 1.33 1.99 5 0.00 0.00 0.00 0.00 0.00 5.00 100.00 1.33 1.99 6 402.00 370.00 92.04 98.67 1.83 375.00 92.14 100.00 1.84 7 0.00 0.00 0.00 0.00 0.00 375.00 92.14 100.00 1.84 8 0.00 0.00 0.00 0.00 0.00 375.00 92.14 100.00 1.84 9 0.00 0.00 0.00 0.00 0.00 375.00 92.14 100.00 1.84 10 340.00 0.00 0.00 0.00 0.00 375.00 50.20 100.00 1.00 56 Lift Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Decision Trees Graphs Tree Browser is displayed as follows: Figure 44: Decision Tree Graph Tutorial: Browser Select the Text Tree radio to view the rules in textual format: Figure 45: Decision Tree Graph Tutorial: Lift Additionally, you can click on Lift Chart to view the contents of the Lift Table graphically. Teradata Warehouse Miner User Guide - Volume 3 57 Chapter 1: Analytic Algorithms Factor Analysis Figure 46: Decision Tree Graph Tutorial: Browser Factor Analysis Overview Consider a data set with a number of correlated numeric variables that is to be used in some type of analysis, such as linear regression or cluster analysis. Or perhaps it is desired to understand customer behavior in a fundamental way, by discovering hidden structure and meaning in data. Factor analysis can be used to reduce a number of correlated numeric variables into a lesser number of variables called factors. These new variables or factors should hopefully be conceptually meaningful if the second goal just mentioned is to be achieved. Meaningful factors not only give insight into the dynamics of a business, but they also make any models built using these factors more explainable, which is generally a requirement for a useful analytic model. There are two fundamental types of factor analysis, principal components and common factors. Teradata Warehouse Miner offers principal components, maximum likelihood common factors and principal axis factors, which is a restricted form of common factor analysis. The product also offers factor rotations, both orthogonal and oblique, as postprocessing for any of these three types of models. Finally, as with all other models, automatic factor model scoring is offered via dynamically generated SQL. Before using the Teradata Warehouse Miner Factor Analysis module, the user must first build a data reduction matrix using the Build Matrix function. The matrix must include all of the input variables to be used in the factor analysis. The user can base the analysis on either a covariance or correlation matrix, thus working with either centered and unscaled data, or centered and normalized data (i.e. unit variance). Teradata Warehouse Miner automatically converts the extended cross-products matrix stored in metadata results tables by the Build 58 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis Matrix function into the desired covariance or correlation matrix. The choice will affect the scaling of resulting factor measures and factor scores. The primary source of information and formulae in this section is [Harman]. Principal Components Analysis The goal of principal components analysis (PCA) is to account for the maximum amount of the original data’s variance in the principal components created. Each of the original variables can be expressed as a linear combination of the new principal components. Each principal component in its turn, from the first to the last, accounts for a maximum amount of the remaining sum of the variances of the original variables. This allows some of the later components to be discarded and only the reduced set of components accounting for the desired amount of total variance to be retained. If all the components were to be retained, then all of the variance would be explained. A principal components solution has many desirable properties. First, the new components are independent of each other, that is, uncorrelated in statistical terminology or orthogonal in the terminology of linear algebra. Further, the principal components can be calculated directly, yielding a unique solution. This is true also of principal component scores, which can be calculated directly from the solution and are also inherently orthogonal or independent of each other. Principal Axis Factors The next step toward the full factor analysis model is a technique known as principal axis factors (PAF), or sometimes also called iterated principal axis factors, or just principal factors. The principal factors model is a blend of the principal components model described earlier and the full common factor model. In the common factor model, each of the original variables is described in terms of certain underlying or common factors, as well as a unique factor for that variable. In principal axis factors however, each variable is described in terms of common factors without a unique factor. Unlike a principal components model for which there is a unique solution, a principal axis factor model consists of estimated factors and scores. As with principal components, the derived factors are orthogonal or independent of each other. The same is not necessarily true of the scores however. (Refer to “Factor Scores” on page 61 for more information). Maximum Likelihood Common Factors The goal of common factors or classical factor analysis is to account in the new factors for the maximum amount of covariance or correlation in the original input variables. In the common factor model, each of the original input variables is expressed in terms of hypothetical common factors plus a unique factor accounting for the remaining variance in that variable. The user must specify the desired number of common factors to look for in the model. This type of model represents factor analysis in the fullest sense. Teradata Warehouse Miner offers maximum likelihood factors (MLF) for estimating common factors, using expectation maximization or EM as the method to determine the maximum likelihood solution. A potential benefit of common factor analysis is that it may reduce the original set of variables into fewer factors than would principal components analysis. It may also produce Teradata Warehouse Miner User Guide - Volume 3 59 Chapter 1: Analytic Algorithms Factor Analysis new variables that have more fundamental meaning. A drawback is that factors can only be estimated using iterative techniques requiring more computation, as there is no unique solution to the common factor analysis model. This is true also of common factor scores, which must likewise be estimated. As with principal components and principal axis factors, the derived factors are orthogonal or independent of each other, but in this case by design (Teradata Warehouse Miner utilizes a technique to insure this). The same is not necessarily true of the factor scores however. (Refer to “Factor Scores” on page 61 for more information). These three types of factor analysis then give the data analyst the choice of modeling the original variables in their entirety (principal components), modeling them with hypothetical common factors alone (principal axis factors), or modeling them with both common factors and unique factors (maximum likelihood common factors). Factor Rotations Whatever technique is chosen to compute principal components or common factors, the new components or factors may not have recognizable meaning. Correlations will be calculated between the new factors and the original input variables, which presumably have business meaning to the data analyst. But factor-variable correlations may not possess the subjective quality of simple structure. The idea behind simple structure is to express each component or factor in terms of fewer variables that are highly correlated with the factor (or vice versa), with the remaining variables largely uncorrelated with the factor. This makes it easier to understand the meaning of the components or factors in terms of the variables. Factor rotations of various types are offered to allow the data analyst to attempt to find simple structure and hence meaning in the new components or factors. Orthogonal rotations maintain the independence of the components or factors while aligning them differently with the data to achieve a particular simple structure goal. Oblique rotations relax the requirement for factor independence while more aggressively seeking better data alignment. Teradata Warehouse Miner offers several options for both orthogonal and oblique rotations. Factor Loadings The term factor loadings is sometimes used to refer to the coefficients of the linear combinations of factors that make up the original variables in a factor analysis model. The appropriate term for this however is the factor pattern. A factor loadings matrix is sometimes also assumed to indicate the correlations between the factors and the original variables, for which the appropriate term is factor structure. The good news is that whenever factors are mutually orthogonal or independent of each other, the factor pattern P and the factor structure S are the same. They are related by the equation S = PQ where Q is the matrix of correlations between factors. In the case of principal components analysis, factor loadings are labeled as component loadings and represent both factor pattern and structure. For other types of analysis, loadings are labeled as factor pattern but indicate structure also, unless a separate structure matrix is also given (as is the case after oblique rotations, described later). Keeping the above caveats in mind, the component loadings, pattern or structure matrix is interpreted for its structure properties in order to understand the meaning of each new factor 60 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis variable. When the analysis is based on a correlation matrix, the loadings, pattern or structure can be interpreted as a correlation matrix with the columns corresponding to the factors and the rows corresponding to the original variables. Like all correlations, the values range in absolute value from 0 to 1 with the higher values representing a stronger correlation or relationship between the variables and factors. By looking at these values, the user gets an idea of the meaning represented by each factor. Teradata Warehouse Miner stores these so called factor loadings and other related values in metadata result tables to make them available for scoring. Factor Scores In order to use a factor as a variable, it must be assigned a value called a factor score for each row or observation in the data. A factor score is actually a linear combination of the original input variables (without a constant term), and the coefficients associated with the original variables are called factor weights. Teradata Warehouse Miner provides a scoring function that calculates these weights and creates a table of new factor score variables using dynamically generated SQL. The ability to automatically generate factor scores, regardless of the factor analysis or rotation options used, is one of the most powerful features of the Teradata Warehouse Miner factor analysis module. Principal Components As mentioned earlier in the introduction, the goal of principal components analysis (PCA) is to account for the maximum amount of the original data’s variance in the independent principal components created. It was also stated that each of the original variables is expressed as a linear combination of the new principal components, and that each principal component in its turn, from the first to the last, accounts for a maximum amount of the remaining sum of the variances of the original variables. These results are achieved by first finding the eigenvalues and eigenvectors of the covariance or correlation matrix of the input variables to be modeled. Although not ordinarily thought of in this way, when analyzing v numeric columns in a table in a relational database, one is in some sense working in a vdimensional vector space corresponding to these columns. Back at the beginning of the previous century when principal components analysis was developed, this was no small task. Today however math library routines are available to perform these computations very efficiently. Although it won’t be attempted here to derive the mathematical solution to finding principal components, it might be helpful to state the following definition, i.e. that a square matrix A has an eigenvalue and an eigenvector x if Ax = x . Further, a v x v square symmetric matrix A has v pairs of eigenvalues and eigenvectors, 1 e 1 2 e 2 v e v . It is further true that eigenvectors can be found so that they have unit length and are mutually orthogonal, i.e. independent or uncorrelated, making them unique. To return to the point at hand, the principal component loadings that are being sought are actually the covariance or correlation matrix eigenvectors just described multiplied by the square root of their respective eigenvalues. The step left out up to now however is the reduction of these principal component loadings to a number fewer than the variables present at the start. This can be achieved by first ordering the eigenvalues, and their corresponding eigenvectors, from maximum to minimum in descending order, and then by throwing away Teradata Warehouse Miner User Guide - Volume 3 61 Chapter 1: Analytic Algorithms Factor Analysis those eigenvalues below a minimum threshold value, such as 1.0. An alternative technique is to retain a desired number of the largest components regardless of the magnitude of the eigenvalues. Teradata Warehouse Miner provides both of these options to the user. The user may further optionally request that the signs of the principal component loadings be inverted if there are more minus signs than positive ones. This is purely cosmetic and does not affect the solution in a substantive way. However, if signs are reversed, this must be kept in mind when attempting to interpret or assign conceptual meaning to the factors. A final point worth noting is that the eigenvalues themselves turn out to be the variance accounted for by each principal component, allowing the computation of several variance related measures and some indication of the effectiveness of the principal components model. Principal Axis Factors In order to talk about principal axis factors (PAF) the term communality must first be introduced. In the common factor model, each original variable x is thought of to be a combination of common factors and a unique factor. The variance of x can then also be thought of as being composed of a common portion and a unique portion, that is 2 2 Var x = c + u . It is the common portion of the variance of x that is called the communality of x, that is the variance that the variable has in common through the common factors with all the other variables. In the algorithm for principal axis factors described below it is of interest to both make an initial estimate of the communality of each variable, and to calculate the actual communality for the variables in a factor model with uncorrelated factors. One method of making an initial estimate of the communality of each variable is to take the largest correlation of that variable with respect to the other variables. The preferred method however is to calculate its squared multiple correlation coefficient with respect to all of the other variables taken as a whole. This is the technique used by Teradata Warehouse Miner. The multiple correlation coefficient is a measure of the overall linear association of one variable with several other variables, that is, the correlation between a variable and the best-fitting linear combination of the other variables. The square of this value has the useful property of being a lower bound for the communality. Once a factor model is built, the actual communality of a variable is simply the sum of the squares of the factor loadings, i.e. 2 hj = r k – 1 fjk 2 With the idea of communality thus in place it is straightforward to describe the principal axis factors algorithm. Begin by estimating the communality of each variable and replacing this value in the appropriate position in the diagonal of the correlation or covariance matrix being factored. Then a principal components solution is found in the usual manner, as described earlier. As before, the user has the option of specifying either a fixed number of desired factors or a minimum eigenvalue by which to reduce the number of factors in the solution. Finally, the new communalities are calculated as the sum of the squared factor loadings, and these values are substituted into the correlation or covariance matrix. This process is repeated until the communalities change by only a small amount. 62 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis Through its use of communality estimates, the principal axis factor method attempts to find independent common factors that account for the covariance or correlation between the original variables in the model, while ignoring the effect of unique factors. It is then possible to use the factor loadings matrix to reproduce the correlation or covariance matrix and compare this to the original as a way of assessing the effectiveness of the model. The reproduced correlation or covariance matrix is simply the factor loadings matrix times its transpose, i.e. CCT. The user may optionally request that the signs of the factor loadings be inverted if there are more minus signs than positive ones. This is purely cosmetic and does not affect the solution in a substantive way. However, if signs are reversed, this must be kept in mind when attempting to interpret or assign meaning to the factors. Maximum Likelihood Factors As mentioned earlier, the common factor model attempts to find both common and unique factors explaining the covariance or correlations amongst a set of variables. That is, an attempt is made to find a factor pattern C and a uniqueness matrix R such that a covariance or correlation matrix S can be modeled as S = CCT + R. To do this, it is necessary to utilize the principle of maximum likelihood based on the assumption that the data comes from a multivariate normal distribution. Due to dealing with the distribution function of the elements of a covariance matrix it is necessary to use the Wishart distribution in order to derive the likelihood equation. The optimization technique used then to maximize the likelihood of a solution for C and R is the Expectation Maximization or EM technique. This technique, often used in the replacement of missing data, is the same basic technique used in Teradata Warehouse Miner’s cluster analysis algorithm. Some key points regarding this technique are described below. Beginning with a correlation or covariance matrix S as with our other factor techniques, a principal components solution is first derived as an initial estimate for the factor pattern matrix C, with the initial estimate for the uniqueness matrix R taken simply as S - CCT. Then the maximum likelihood solution is iteratively found, yielding a best estimate of C and R. In order then to assess the effectiveness of the model, the correlation or covariance matrix S is compared to the reproduced matrix CCT - R. It should be pointed out that when using the maximum likelihood solution the user must first specify the number of common factors f to produce in the model. The software will not automatically determine what this value should be or determine it based on a threshold value. Also, an internal adjustment is made to the final factor pattern matrix C to make the factors orthogonal, something that is automatically true of the other factor solutions. Finally, the user may optionally request that the signs of a factor in the matrix C be inverted if there are more minus signs than positive ones. This is purely cosmetic and does not affect the solution in a substantive way. However, if signs are reversed, this must be kept in mind when attempting to interpret or assign meaning to the factors. Factor Rotations Teradata Warehouse Miner offers a number of techniques for rotating factors in order to find the elusive quality of simple structure described earlier. These may optionally be used in combination with any of the factor techniques offered in the product. When a rotation is performed, both the rotated matrix and the rotation matrix is reported, as well as the Teradata Warehouse Miner User Guide - Volume 3 63 Chapter 1: Analytic Algorithms Factor Analysis reproduced correlation or covariance matrix after rotation. As before with the factor solutions themselves, the user may optionally request that the signs of a factor in the rotated factor or components matrix be inverted if there are more minus signs than positive ones. This is purely cosmetic and does not affect the solution in a substantive way. Orthogonal rotations First consider orthogonal rotations, that is, rotations of a factor matrix A that result in a rotated factor matrix B by way of an orthogonal transformation matrix T, i.e. B = AT. Remember that the nice thing about orthogonal rotations on a factor matrix is that the resulting factors scores are uncorrelated, a desirable property when the factors are going to be used in subsequent regression, cluster or other type of analysis. But how is simple structure obtained? As described earlier, the idea behind simple structure is to express each component or factor in terms of fewer variables that are highly correlated with the factor, with the remaining variables not so correlated with the factor. The two most famous mathematical criteria for simple factor structure are the quartimax and varimax criteria. Simply put, the varimax criterion seeks to simplify the structure of columns or factors in the factor loading matrix, whereas the quartimax criterion seeks to simplify the structure of the rows or variables in the factor loading matrix. Less simply put, the varimax criterion seeks to maximize the variance of the squared loadings across the variables for all factors. The quartimax criterion seeks to maximize the variance of the squared loadings across the factors for all variables. The solution to either optimization problem is mathematically quite involved, though in principle it is based on fundamental techniques of linear algebra, differential calculus, and the use of the popular Newton-Raphson iterative technique for finding the roots of equations. Regardless of the criterion used, rotations are performed on normalized loadings, that is prior to rotating, the rows of the factor loading matrix are set to unit length by dividing each element by the square root of the communality for that variable. The rows are un-normalized back to the original length after the rotation is performed. This has been found to improve results, particularly for the varimax method. Fortunately both the quartimax and varimax criteria can be expressed in terms of the same equation containing a constant value that is 0 for quartimax and 1 for varimax. The orthomax criterion is then obtained simply by setting this constant, call it gamma, to any desired value, equamax corresponds to setting this constant to half the number of factors, and parsimax is given by setting the value of gamma to v(f-1) / (v+f+2) where v is the number of variables and f is the number of factors. Oblique rotations As mentioned earlier, oblique rotations relax the requirement for factor independence that exists with orthogonal rotations, while more aggressively seeking better data alignment. Teradata Warehouse Miner uses a technique known as the indirect oblimin method. As with orthogonal rotations, there is a common equation for the oblique simple structure criterion that contains a constant that can be set for various effects. A value of 0 for this constant, call it gamma, yields the quartimin solution, which is the most oblique solution of those offered. A value of 1 yields the covarimin solution, the least oblique case. And a value of 0.5 yields the 64 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis biquartimin solution, a compromise between the two. A solution known as orthomin can be achieved by setting the value of gamma to any desired positive value. One of the distinctions of a factor solution that incorporates an oblique rotation is that the factor loadings must be thought of in terms of two different matrices, the factor pattern P matrix and the factor structure matrix S. These are related by the equation S = PQ where Q is the matrix of correlations between factors. Obviously if the factors are not correlated, as in an un-rotated solution or after an orthogonal rotation, then Q is the identity matrix and the structure and pattern matrix are the same. The result of an oblique rotation must include both the pattern matrix that describes the common factors and the structure matrix of correlations between the factors and original variables. As with orthogonal rotations, oblique rotations are performed on normalized loadings that are restored to their original size after rotation. A unique characteristic of the indirect oblimin method of rotation is that it is performed on a reference structure based on the normals of the original factor space. There is no inherent value in this, but is in fact just a side effect of the technique. It means however that an oblique rotation results in a reference factor pattern, structure and rotation matrix that is then converted back into the original factor space as the final primary factor pattern, structure and rotation matrix. Data Quality Reports The same data quality reports optionally available for linear regression are also available when performing Factor Analysis. Prime Factor Reports Prime Factor Loadings This report provides a specially sorted presentation of the factor loadings. Like the standard report of factor loadings, the rows represent the variables and the columns represent the factors. In this case, however, each variable is associated with the factor for which it has the largest loading as an absolute value. The variables having factor 1 as the prime factor are listed first, in descending order of the loading with factor 1. Then the variables having factor 2 as the prime factor are listed, continuing on until all the variables are listed. It is possible that not all factors will appear in the Prime Factor column, but all the variables will be listed once and only once with all their factor loadings. Note that in the special case after an oblique rotation has been performed in the factor analysis, the report is based on the factor structure matrix and not the factor pattern matrix, since the structure matrix values represent the correlations between the variables and the factors. The following is an example of a Prime Factor Loadings report. Table 14: Prime Factor Loadings report (Example) Variable Prime Factor Factor 1 Factor 2 Factor 3 income Factor 1 .8229 -1.1675E-02 .1353 revenue Factor 1 .8171 .4475 2.3336E-02 Teradata Warehouse Miner User Guide - Volume 3 65 Chapter 1: Analytic Algorithms Factor Analysis Table 14: Prime Factor Loadings report (Example) Variable Prime Factor Factor 1 Factor 2 Factor 3 single Factor 1 -.7705 .4332 .1554 age Factor 1 .7348 -4.5584E-02 1.0212E-02 cust_years Factor 2 .5158 .6284 .1577 purchases Factor 2 .5433 -.5505 -.254 female Factor 3 -4.1177E-02 .3366 -.9349 Prime Factor Variables The Prime Factor Variables report is closely related to the Prime Factor Loadings report. It associates variables with their prime factors and possibly other factors if a threshold percent or loading value is specified. It provides a simple presentation, without numbers, of the relationships between factors and the variables that contribute to them. If a threshold percent of 1.0 is used, only prime factor relationships are reported. A threshold percentage of less than 1.0 indicates that if the loading for a particular factor is equal to or above this percentage of the loading for the variable's prime factor, then an association is made between the variable and this factor as well. When the variable is associated with a factor other than its prime factor, the variable name is given in parentheses. A threshold loading value may alternately be used to determine the associations between variables and factors. In this case, it is possible that a variable may not appear in the report, depending on the threshold value and the loading values. However, if the option to reverse signs was enabled, positive values may actually represent inverse relationships between factors and original variables. Deselecting this option in a second run and examining factor loading results will provide the true nature (directions) of relationships among variables and factors. The following is an example of a Prime Factor Variables report. Table 15: Prime Factor Variables report (Example) 66 Factor 1 Factor 2 Factor 3 income cust_years female revenue purchases * single * * age * * (purchases) * * Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis Prime Factor Variables with Loadings The Prime Factor Variables with Loadings is functionally the same as the Prime Factor Variables report except that the actual loading values determining the associations between the variables and factors are also given. The magnitude of the loading gives some idea of the relative strength of the relationship and the sign indicates whether or not it is an inverse relationship (a negative sign indicates an inverse relationship in the values, i.e. a negative correlation). The following is an example of a Prime Factor Variables with Loadings report. Table 16: Factor Variable Loading Factor 1 income .8229 Factor 1 revenue .8171 Factor 1 single -.7705 Factor 1 age .7348 Factor 1 (purchases) .5433 Factor 2 cust_years .6284 Factor 2 purchases -.5505 Factor 3 female -.9349 Missing Data Null values for columns in a factor analysis can adversely affect results. It is recommended that the listwise deletion option be used when building the SSCP matrix with the Build Matrix function. This ensures that any row for which one of the columns is null will be left out of the matrix computations completely. Additionally, the Recode transformation function can be used to build a new column, substituting a fixed known value for null. Initiate a Factor Analysis Use the following procedure to initiate a new Factor Analysis in Teradata Warehouse Miner: Teradata Warehouse Miner User Guide - Volume 3 67 Chapter 1: Analytic Algorithms Factor Analysis 1 Click on the Add New Analysis icon in the toolbar: Figure 47: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Analytics under Categories and then under Analyses double-click on Factor Analysis: Figure 48: Add New Analysis dialog 3 This will bring up the Factor Analysis dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Factor - INPUT - Data Selection On the Factor Analysis dialog click on INPUT and then click on data selection: Figure 49: Factor Analysis > Input > Data Selection 68 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis On this screen select: 1 Select Input Source Users may select between different sources of input, Table, Matrix or Analysis. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. (In this case a matrix will be dynamically built and discarded when the algorithm completes execution). By selecting the Input Source Matrix the user may can select from available matrices created by the Build Matrix function. This has the advantage that the matrix selected for input is available for further analysis after completion of the algorithm, perhaps selecting a different subset of columns from the matrix. By selecting the Input Source Analysis the user can select directly from the output of another analysis of qualifying type in the current project. (In this case a matrix will be dynamically built and discarded when the algorithm completes execution). Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 Select Columns From One Table • Available Databases (only for Input Source equal to Table) — All the databases that are available for the Factor Analysis. • Available Matrices (only for Input Source equal to Matrix) — When the Input Source is Matrix, a matrix must first be built by the user with the Build Matrix function before Factor Analysis can be performed. Select the matrix that summarizes the data to be analyzed. (The matrix must have been built with more rows than columns selected or the Factor Analysis will produce a singular matrix, causing a failure). • Available Analyses (only for Input Source equal to Analysis) — All the analyses that are available for the Factor Analysis. • Available Tables (only for Input Source equal to Table or Analysis) — All the tables that are available for the Factor Analysis. • Available Columns — All the columns that are available for the Factor Analysis. • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. The algorithm requires that the selected columns be of numeric type (or contain numbers in character format). Factor - INPUT - Analysis Parameters On the Factor Analysis dialog click on INPUT and then click on analysis parameters: Teradata Warehouse Miner User Guide - Volume 3 69 Chapter 1: Analytic Algorithms Factor Analysis Figure 50: Factor Analysis > Input > Analysis Parameters On this screen select: • General Options • • Analysis method • Principal Components (PCA) — As described above. This is the default method. • Principal Axis Factors (PAF) — As described above. • Maximum Likelihood Factors (MLF) — As described above. Convergence Method • Minimum Eigenvalue PCA — minimum eigenvalue to include in principal components (default 1.0) PAF — minimum eigenvalue to include in factor loadings (default 0.0) MLF — option does not apply (N/A) • • • • 70 Number of Factors — The user may request a specific number of factors as an alternative to using the minimum eigenvalue option for PCA and PAF. Number of factors is however required for MLF. The number of factors requested must not exceed the number of requested variables. Convergence Criterion • PCA — convergence criterion does not apply • PAF — iteration continues until maximum communality change does not exceed convergence criterion • MLF — iteration continues until maximum change in the square root of uniqueness values does not exceed convergence criterion Maximum Iterations • PCA — maximum iterations does not apply (N/A) • PAF — the algorithm stops if the maximum iterations is exceeded (default 100) • MLF — the algorithm stops if the maximum iterations is exceeded (default 1000) Matrix Type — The product automatically converts the extended cross-products matrix stored in metadata results tables by the Build Matrix function into the desired covariance or correlation matrix. The choice will affect the scaling of resulting factor measures and factor scores. • Correlation — Build a correlation matrix as input to Factor Analysis. This is the default option. • Covariance — Build a covariance matrix as input to Factor Analysis. • Invert signs if majority of matrix values are negative (checkbox) — You may Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis optionally request that the signs of factor loadings and related values be changed if there are more minus signs than positive ones. This is purely cosmetic and does not affect the solution in a substantive way. Default is enabled. • Rotation Options • Rotation Method • None — No factor rotation is performed. This is the default option. • Varimax — Gamma in rotation equation fixed at 1.0. The varimax criterion seeks to simplify the structure of columns or factors in the factor loading matrix • Quartimax — Gamma in rotation equation fixed at 0.0. the quartimax criterion seeks to simplify the structure of the rows or variables in the factor loading matrix • Equamax — Gamma in rotation equation fixed at f / 2. • Parsimax — Gamma in rotation equation fixed at v(f-1) / (v+f+2). • Orthomax — Gamma in rotation equation set by user. • Quartimin — Gamma in rotation equation fixed at 0.0. Provides the most oblique rotation. • Biquartimin — Gamma in rotation equation fixed at 0.5. • Covarimin — Gamma in rotation equation fixed at 1.0. Provides the least oblique rotation. • Orthomin — Gamma in rotation equation set by user. • Report Options • Variable Statistics — This report gives the mean value and standard deviation of each variable in the model based on the derived SSCP matrix. • Near Dependency — This report lists collinear variables or near dependencies in the data based on the derived SSCP matrix. • Condition Index Threshold — Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The one that involves this parameter is the occurrence of a large condition index value associated with a specially constructed principal factor. If a factor has a condition index greater than this parameter’s value, it is a candidate for the Near Dependency report. A default value of 30 is used as a rule of thumb. • Variance Proportion Threshold — Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The one that involves this parameter is when two or more variables have a variance proportion greater than this threshold value for a factor with a high condition index. Another way of saying this is that a ‘suspect’ factor accounts for a high proportion of the variance of two or more variables. This parameter defines what a high proportion of variance is. A default value of 0.5 is used as a rule of thumb. • Collinearity Diagnostics Report — This report provides the details behind the Near Dependency report, consisting of the “Eigenvalues of Unit Scaled X’X”, “Condition Indices” and “Variance Proportions” tables. • Factor Loading Reports • Factor Variables Report Teradata Warehouse Miner User Guide - Volume 3 71 Chapter 1: Analytic Algorithms Factor Analysis • Factor Variables with Loadings Report • Display Variables Using • Threshold percent • Threshold loading — A threshold percentage of less than 1.0 indicates that if the loading for a particular factor is equal or above this percentage of the loading for the variable's prime factor, then an association is made between the variable and this factor as well. A threshold loading value may alternatively be used. Run the Factor Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Factor Analysis The results of running the Factor Analysis include a factor patterns graph, a scree plot (unless MLF was specified), and a variety of statistic reports. All of these results are outlined below. Factor Analysis - RESULTS - Reports On the Factor Analysis dialog, click on RESULTS and then click on reports (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 51: Factor Analysis > Results > Reports Data Quality Reports • Variable Statistics — If selected on the Results Options tab, this report gives the mean value and standard deviation of each variable in the model based on the SSCP matrix provided as input. • Near Dependency — If selected on the Results Options tab, this report lists collinear variables or near dependencies in the data based on the SSCP matrix provided as input. Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The first is the occurrence of a large condition index value associated with a specially constructed principal factor. If a factor has a condition index greater than the parameter specified on the Results Option tab, it is a candidate for the Near Dependency report. The other is when two or more variables have a variance proportion greater than a threshold value for a factor with a high condition index. Another way of 72 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis saying this is that a ‘suspect’ factor accounts for a high proportion of the variance of two or more variables. The parameter to defines what a high proportion of variance is also set on the Results Option tab. A default value of 0.5. • Detailed Collinearity Diagnostics — If selected on the Results Options tab, this report provides the details behind the Near Dependency report, consisting of the following tables. • Eigenvalues of Unit Scaled X'X — Report of the eigenvalues of all variables scaled so that each variable adds up to 1 when summed over all the observations or rows. In order to calculate the singular values of X (the rows of X are the observations), the mathematically equivalent square root of the eigenvalues of XTX are computed instead for practical reasons • Condition Indices — The condition index of each eigenvalue, calculated as the square root of the ratio of the largest eigenvalue to the given eigenvalue, a value always 1 or greater. • Variance Proportions — The variance decomposition of these eigenvalues is computed using the eigenvalues together with the eigenvectors associated with them. The result is a matrix giving, for each variable, the proportion of variance associated with each eigenvalue. Principal Component Analysis report • Number of Variables — This is the number of variables to be factored, taken from the matrix that is input to the algorithm. Note that there are no dependent or independent variables in a factor analysis model. • Minimum Eigenvalue — The minimum value of a factor’s associated eigenvalue, determining whether or not to include the factor in the final model. This field is not displayed if the Number of Factors option is used to determine the number of factors retained. • Number of Factors — This value reflects the number of factors retained in the final factor analysis model. If the Number of Factors option is explicitly set by the user to determine the number of factors, then this reported value reflects the value set by the user. Otherwise, it reflects the number of factors resulting from applying the Minimum Eigenvalue option. • Matrix Type (cor/cov) — This value reflects the type of input matrix requested by the user, either correlation (cor) or covariance (cov). • Rotation (none/orthogonal/oblique) — This value reflects the type of rotation, if any, requested by the user, either none, orthogonal, or oblique. • Gamma — This value is a coefficient in the rotation equation that reflects the type of rotation requested, if any, and in some cases is explicitly set by the user. Gamma is determined as follows. • Orthogonal rotations: • Varimax — (gamma in rotation equation fixed at 1.0) • Quartimax — (gamma in rotation equation fixed at 0.0) • Equamax — (gamma in rotation equation fixed at f / 2)* Teradata Warehouse Miner User Guide - Volume 3 73 Chapter 1: Analytic Algorithms Factor Analysis • Parsimax — (gamma in rotation equation fixed at v(f-1) / (v+f+2))* • Orthomax — (gamma in rotation equation set by user) * where v is the number of variables and f is the number of factors • Oblique rotations • Quartimin — (gamma in rotation equation fixed at 0.0) • Biquartimin — (gamma in rotation equation fixed at 0.5) • Covarimin — (gamma in rotation equation fixed at 1.0) • Orthomin — (gamma in rotation equation set by user) Principal Axis Factors report • Number of Variables — This is the number of variables to be factored, taken from the matrix that is input to the algorithm. Note that there are no dependent or independent variables in a factor analysis model. • Minimum Eigenvalue — The minimum value of a factor’s associated eigenvalue, determining whether or not to include the factor in the final model. This field is not displayed if the Number of Factors option is used to determine the number of factors retained. • Number of Factors — This value reflects the number of factors retained in the final factor analysis model. If the Number of Factors option is explicitly set by the user to determine the number of factors, then this reported value reflects the value set by the user. Otherwise, it reflects the number of factors resulting from applying the Minimum Eigenvalue option. • Maximum Iterations — This is the maximum number of iterations requested by the user. • Convergence Criterion — This is the value requested by the user as the convergence criterion such that iteration continues until the maximum change in the square root of uniqueness values does not exceed this value. • Rotation (none/orthogonal/oblique) — This value reflects the type of rotation, if any, requested by the user, either none, orthogonal, or oblique. • Gamma — This value is a coefficient in the rotation equation that reflects the type of rotation requested, if any, and in some cases is explicitly set by the user. Gamma is determined as follows. • Orthogonal rotations • Varimax — (gamma in rotation equation fixed at 1.0) • Quartimax — (gamma in rotation equation fixed at 0.0) • Equamax — (gamma in rotation equation fixed at f / 2)* • Parsimax — (gamma in rotation equation fixed at v(f-1) / (v+f+2))* • Orthomax — (gamma in rotation equation set by user) * where v is the number of variables and f is the number of factors • 74 Oblique rotations • Quartimin — (gamma in rotation equation fixed at 0.0) • Biquartimin — (gamma in rotation equation fixed at 0.5) Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis • Covarimin — (gamma in rotation equation fixed at 1.0) • Orthomin — (gamma in rotation equation set by user) Maximum Likelihood (EM) Factor Analysis report • Number of Variables — This is the number of variables to be factored, taken from the matrix that is input to the algorithm. Note that there are no dependent or independent variables in a factor analysis model. • Number of Observations — This is the number of observations in the data used to build the matrix that is input to the algorithm. • Number of Factors — This reflects the number of factors requested by the user for the factor analysis model. • Maximum Iterations — This is the maximum number of iterations requested by the user. (The actual number of iterations used is reflected in the Total Number of Iterations field further down in the report). • Convergence Criterion — This is the value requested by the user as the convergence criterion such that iteration continues until the maximum change in the square root of uniqueness values does not exceed this value. (It should be noted that convergence is based on uniqueness values rather than maximum likelihood values, something that is done strictly for practical reasons based on experimentation). • Matrix Type (cor/cov) — This value reflects the type of input matrix requested by the user, either correlation (cor) or covariance (cov). • Rotation (none/orthogonal/oblique) — This value reflects the type of rotation, if any, requested by the user, either none, orthogonal, or oblique. • Gamma — This value is a coefficient in the rotation equation that reflects the type of rotation requested, if any, and in some cases is explicitly set by the user. Gamma is determined as follows. • Orthogonal rotations • Varimax — (gamma in rotation equation fixed at 1.0) • Quartimax — (gamma in rotation equation fixed at 0.0) • Equamax — (gamma in rotation equation fixed at f / 2)* • Parsimax — (gamma in rotation equation fixed at v(f-1) / (v+f+2))* • Orthomax — (gamma in rotation equation set by user) * where v is the number of variables and f is the number of factors • Oblique rotations • Quartimin — (gamma in rotation equation fixed at 0.0) • Biquartimin — (gamma in rotation equation fixed at 0.5) • Covarimin — (gamma in rotation equation fixed at 1.0) • Orthomin — (gamma in rotation equation set by user) • Total Number of Iterations — This value is the number of iterations that the algorithm performed to converge on a maximum likelihood solution. Teradata Warehouse Miner User Guide - Volume 3 75 Chapter 1: Analytic Algorithms Factor Analysis • Final Average Likelihood — This is the final value of the average likelihood over all the observations represented in the input matrix. • Change in Avg Likelihood — This is the final change, from the previous to the final iteration, in value of the average likelihood over all the observations represented in the input matrix. • Maximum Change in Sqrt (uniqueness) — The algorithm calculates a uniqueness value for each factor each time it iterates, and keeps track of how much the positive square root of each of these values changes from one iteration to the next. The maximum change in this value is given here, and it is of interest because it is used to determine convergence of the model. (Refer to “Final Uniqueness Values” on page 78 for an explanation of these values in the common factor model). Max Change in Sqrt (Communality) For Each Iteration This report, printed for Principal Axis Factors only, and only if the user requests the Report Output option Long, shows the progress of the algorithm in converging on a solution. It does this by showing, at each iteration, the maximum change in the positive square root of the communality of each of the variables. The communality of a variable is that portion of its variance that can be attributed to the common factors. Simply put, when the communality values for all of the variables stop changing sufficiently, the algorithm stops. Matrix to be Factored The correlation or covariance matrix to be factored is printed out only if the user requests the Report Output option Long. Only the lower triangular portion of this symmetric matrix is reported and output is limited to at most 100 rows for expediency. (If it is necessary to view the entire matrix, the Get Matrix function with the Export to File option is recommended). Initial Communality Estimates This report is produced only for Principal Axis Factors and Maximum Likelihood Factors. The communality of a variable is that portion of its variance that can be attributed to the common factors, excluding uniqueness. The initial communality estimates for each variable are made by calculating the squared multiple correlation coefficient of each variable with respect to the other variables taken together. Final Communality Estimates This report is produced only for Principal Axis Factors and Maximum Likelihood Factors. The communality of a variable is that portion of its variance that can be attributed to the common factors, excluding uniqueness. The final communality estimates for each variable are computed as: 2 hj = r k – 1 fjk 2 i.e. as the sum of the squares of the factor loadings for each variable. 76 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis Eigenvalues These are the resulting eigenvalues of the principal component or principal axis factor solution, in descending order. At this stage, there are as many eigenvalues as input variables since the number of factors has not been reduced yet. Eigenvectors These are the resulting eigenvectors of the principal components or principal axis factor solution, in descending order. At this stage, there are as many eigenvectors as input variables since the number of factors has not been reduced yet. Eigenvectors are printed out only if the user requests the Report Output option Long. Principal Component Loadings (Principal Components) This matrix of values, which is variables by factors in size, represents both the factor pattern and factor structure, i.e. the linear combination of factors for each variable and the correlations between factors and variables (provided Matrix Type is Correlation). The number of factors has been reduced to meet the minimum eigenvalue or number of factors requested, but the output does not reflect any factor rotations that may have been requested. This output table contains the raw data used in the Prime Factor Reports, which are probably better to use for interpreting results. If the user requested a Matrix Type of Correlation, the principal component loadings can be interpreted as the correlations between the original variables and the newly created factors. An absolute value approaching 1 indicates that a variable is contributing strongly to a particular factor. Factor Pattern (Principal Axis Factors) This matrix of values, which is variables by factors in size, represents both the factor pattern and factor structure, i.e. the linear combination of factors for each variable and the correlations between factors and variables (provided Matrix Type is Correlation). The number of factors has been reduced to meet the minimum eigenvalue or number of factors requested, but the output does not reflect any factor rotations that may have been requested. This output table contains the raw data used in the Prime Factor Reports, which are probably better to use for interpreting results. If the user requested a Matrix Type of Correlation, the factor pattern can be interpreted as the correlations between the original variables and the newly created factors. An absolute value approaching 1 indicates that a variable is contributing strongly to a particular factor. Factor Pattern (Maximum Likelihood Factors) This matrix of values, which is variables by factors in size, represents both the factor pattern and factor structure, i.e. the linear combination of factors for each variable and the correlations between factors and variables (provided Matrix Type is Correlation). The number of factors has been fixed at the number of factors requested. The output at this stage does not reflect any factor rotations that may have been requested. This output table contains the raw data used in the Prime Factor Reports, which are probably better to use for interpreting results. If the user requested a Matrix Type of Correlation, the factor pattern can be interpreted as the correlations between the original variables and the Teradata Warehouse Miner User Guide - Volume 3 77 Chapter 1: Analytic Algorithms Factor Analysis newly created factors. An absolute value approaching 1 indicates that a variable is contributing strongly to a particular factor. Variance Explained by Factors This report provides the amount of variance in all of the original variables taken together that is accounted for by each factor. For Principal Components and Principal Axis Factor solutions, the variance is the same as the eigenvalues calculated for the solution. In general however, and for Maximum Likelihood Factor solutions in particular, the variance is the sum of the squared loadings for each factor. (After an oblique rotation, if the factors are correlated, there is an interaction term that must also be added in based on the loadings and the correlations between factors. A separate report entitled Contributions of Rotated Factors To Variance is provided if an oblique rotation is performed). • Factor Variance — This column shows the actual amount of variance in the original variables accounted for by each factor. • Percent of Total Variance — This column shows the percentage of the total variance in the original variables accounted for by each factor. • Cumulative Percent — This column shows the cumulative percentage of the total variance in the original variables accounted for by Factor 1 through each subsequent factor in turn. Factor Variance to Total Variance Ratio This is simply the ratio of the variance explained by all the factors to the total variance in the original data. Condition Indices of Components The condition index of a principal component or principal factor is the square root of the ratio of the largest eigenvalue to the eigenvalue associated with that component or factor. This report is provided for Principal Components and Principal Axis Factors only. Final Uniqueness Values The common factor model seeks to find a factor pattern C and a uniqueness matrix R such that a covariance or correlation matrix S can be modeled as S = CCT + R. The uniqueness matrix is a diagonal matrix, so there is a single uniqueness value for each variable in the model. The theory behind the uniqueness value of a variable is that the variance of each variable can be expressed as the sum of its communality and uniqueness, that is the variance of the jth variable is given by: 2 2 2 sj = hj + uj This report is provided for Maximum Likelihood Factors only. Reproduced Matrix Based on Loadings The results of a factor analysis can be used to reproduce or approximate the original correlation or covariance matrix used to build the factor analysis model. This is done to evaluate the effectiveness of the model in accounting for the variance in the original data. For 78 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis Principal Components and Principal Axis Factors the reproduced matrix is simply the loadings matrix times its transpose. For Maximum Likelihood Factors it is the loadings matrix times its transpose plus the uniqueness matrix. This report is provided only when Long is selected as the Output Option. Difference Between Original and Reproduced cor/cov Matrix This report gives the differences between the original correlation or covariance matrix values used in the factor analysis and the Reproduced Matrix Based on Loadings. (In the case of Principal Axis Factors, the reproduced matrix is compared to the original matrix with the initial communality estimates placed in the diagonal of the matrix). This report is provided only when Long is selected as the Output Option. Absolute Difference This report summarizes the absolute value of the differences between the original correlation or covariance matrix values used in the factor analysis and the Reproduced Matrix Based on Loadings. • Mean — This is the average absolute difference in correlation or covariance over the entire matrix. • Standard Deviation — This is the standard deviation of the absolute differences in correlation or covariance over the entire matrix. • Minimum — This is the minimum absolute difference in correlation or covariance over the entire matrix. • Maximum — This is the maximum absolute difference in correlation or covariance over the entire matrix. Rotated Loading Matrix This report of the factor loadings (pattern) after rotation is given only after orthogonal rotations. Rotated Structure This report of the factor structure after rotation is given only after oblique rotations. Note that after an oblique rotation the rotated structure matrix is usually different from the rotated pattern matrix. Rotated Pattern This report of the factor pattern after rotation is given only after oblique rotations. Note that after an oblique rotation the rotated pattern matrix is usually different from the rotated structure matrix. Rotation Matrix After rotating the factor pattern matrix P to get the rotated matrix PR, the rotation matrix T is also produced such that PR = PT. However, after an oblique rotation the rotation matrix obeys the following equation: PR = P(TT)-1. This report is provided only when Long is selected as the Output Option. Teradata Warehouse Miner User Guide - Volume 3 79 Chapter 1: Analytic Algorithms Factor Analysis Variance Explained by Rotated Factors This is the same report as Variance Explained by Factors except that it is based on the rotated factor loadings. Comparison of the two reports can show the effects of rotation on the effectiveness of the model. After an oblique rotation, another report is produced called the Contributions of Rotated Factors to Variance to show both the contributions of individual factors and the contributions of factor interactions to the explanation of the variance in the original variables analyzed. Rotated Factor Variance to Total Variance Ratio This is the same report as Factor Variance to Total Variance Ratio except that it is based on the rotated factor loadings. Comparison of the two reports can show the effects of rotation on the effectiveness of the model. Correlations Among Rotated Factors After an oblique rotation the factors are generally no longer orthogonal or uncorrelated with each other. This report is a standard Pearson product-moment correlation matrix treating the rotated factors as new variables. Values range from 0 to -1 or +1 indicating no correlation to maximum correlation respectively (a negative correlation indicates that two factors vary in opposite directions with respect to each other). This report is provided only after an oblique rotation is performed. Contributions of Rotated Factors to Variance In general, the variance of the original variables explained by a factor is the sum of the squared loadings for the factor. But after an oblique rotation the factors may be correlated, so additional interaction terms between the factors must be considered in computing the explained variance reported in the Variance Explained by Rotated Factors report. The contributions of factors to variance may be characterized as direct contributions: n Vp = bjp 2 j=1 and joint contributions: n V pq = 2r Tp Tq b jp b jq j=1 where p and q vary by factors with p < q, j varies by variables, and r is the correlation between factors. The Contributions of Rotated Factors to Variance report displays direct contributions along the diagonal and joint contributions off the diagonal. This report is provided only after an oblique rotation is performed. 80 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis Factor Analysis - RESULTS - Pattern Graph On the Factor Analysis dialog, click on RESULTS and then click on pattern graph (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 52: Factor Analysis > Results > Pattern Graph The Factor Analysis Pattern Graph plots the final factor pattern values for up to twelve variables, two factors at a time. These factor pattern values are the coefficients in the linear combination of factors that comprise each variable. When the Analysis Type is Principal Components, these pattern values are referred to as factor loadings. When the Matrix Type is Correlation, the values of these coefficients are standardized to be between -1 and 1 (if Covariance, they are not). Unless an oblique rotation has been performed, these values also represent the factor structure, i.e. the correlation between a factor and a variable. The following options are available: • Variables • Available — A list of all variables that were input to the Factor Analysis. • Selected — A list the variables (up to 12), that will be displayed on the Factor Patterns graph. • Factors • Available — A list of all factors generated by the Factor Analysis. • Selected — The selected two factors that will be displayed on the Factor Patterns graph. Factor Analysis - RESULTS - Scree Plot Unless MLF was specified, a screen plot is generated. On the Factor Analysis dialog, click on RESULTS and then click on scree plot (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 53: Factor Analysis > Results > Scree Plot A definition of the word scree is a heap of stones or rocky debris, such as at the bottom of a hill. So in a scree plot the object is to find where the plotted points flatten out, in order to determine how many Principal Component or Principal Axis factors should be retained in the factor analysis model (the scree plot does not apply to Maximum Likelihood factor analysis). Teradata Warehouse Miner User Guide - Volume 3 81 Chapter 1: Analytic Algorithms Factor Analysis The plot shows the eigenvalues of each factor in descending order from left to right. Since the eigenvalues represent the amount of variance in the original variables is explained by the factors, when the eigenvalues flatten out in the plot, the factors they represent add less and less to the effectiveness of the model. Tutorial - Factor Analysis In this example, principal components analysis is performed on a correlation matrix for 21 numeric variables. This reduces the variables to 7 factors using a minimum eigenvalue of 1. The Scree Plot supports limiting the number of factors to 7 by showing how the eigenvalues (and thus the explained variance) level off at 7 or above. Parameterize a Factor Analysis as follows: • Available Matrices — Customer_Analysis_Matrix • Selected Variables • income • age • years_with_bank • nbr_children • female • single • married • separated • ccacct • ckacct • svacct • avg_cc_bal • avg_ck_bal • avg_sv_bal • avg_cc_tran_amt • avg_cc_tran_cnt • avg_ck_tran_amt • avg_ck_tran_cnt • avg_sv_tran_amt • avg_sv_tran_cnt • cc_rev • Analysis Method — Principal Components • Matrix Type — Correlation • Minimum Eigenvalue — 1 • Invert signs if majority of matrix values are negative — Enabled • Rotation Options — None 82 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis • Factor Variables — Enabled • Threshold Percent — 1 • Long Report — Not enabled Run the analysis, and click on Results when it completes. For this example, the Factor Analysis generated the following pages. A single click on each page name populates the Results page with the item. Table 17: Factor Analysis Report Number of Variables 21 Minimum Eigenvalue 1 Number of Factors 7 Matrix Type Correlation Rotation None Table 18: Execution Summary 6/20/2004 1:55:02 PM Getting Matrix 6/20/2004 1:55:02 PM Principal Components Analysis Running...x 6/20/2004 1:55:02 PM Creating Report Table 19: Eigenvalues Factor 1 4.292 Factor 2 2.497 Factor 3 1.844 Factor 4 1.598 Factor 5 1.446 Factor 6 1.254 Factor 7 1.041 (Factor 8) .971 (Factor 9) .926 (Factor 10) .871 (Factor 11) .741 (Factor 12) .693 (Factor 13) .601 (Factor 14) .504 Teradata Warehouse Miner User Guide - Volume 3 83 Chapter 1: Analytic Algorithms Factor Analysis Table 19: Eigenvalues (Factor 15) .437 (Factor 16) .347 (Factor 17) .34 (Factor 18) .253 (Factor 19) .151 (Factor 20) .123 (Factor 21) 7.01E-02 Table 20: Principal Component Loadings Variable Name Factor 1 Factor 2 Factor 3 Factor 4 Factor 5 Factor 6 Factor 7 age 0.2876 -0.4711 0.1979 0.2615 0.2975 0.3233 -0.2463 avg_cc_bal -0.7621 0.0131 0.1628 -0.1438 0.3508 -0.1550 -0.0300 avg_cc_tran_amt 0.3716 -0.0318 -0.1360 0.0543 -0.1975 0.0100 0.0971 avg_cc_tran_cnt 0.4704 0.0873 -0.4312 0.5592 -0.0241 0.0133 0.0782 avg_ck_bal 0.5778 0.0527 -0.0981 -0.4598 0.0735 -0.0123 -0.0542 avg_ck_tran_amt 0.7698 0.0386 -0.0929 -0.4535 0.2489 0.0585 0.0190 avg_ck_tran_cnt 0.3127 0.1180 -0.1619 -0.1114 0.5435 0.1845 0.0884 avg_sv_bal 0.3785 0.3084 0.4893 0.0186 -0.0768 -0.0630 0.0517 avg_sv_tran_amt 0.4800 0.4351 0.5966 0.1456 -0.0155 0.0272 0.1281 avg_sv_tran_cnt 0.2042 0.3873 0.4931 0.1144 0.2420 0.0884 -0.0646 cc_rev 0.8377 -0.0624 -0.1534 0.0691 -0.3800 0.1036 0.0081 ccacct 0.2025 0.5213 0.4007 0.3021 0.0499 -0.1988 0.1733 ckacct 0.4007 0.1496 -0.4215 0.5497 0.1127 -0.0818 -0.0086 female -0.0209 0.1165 -0.1357 0.3119 0.1887 -0.2228 -0.3438 income 0.6992 -0.2888 0.1353 -0.2987 -0.2684 0.0733 0.0310 married 0.0595 -0.7702 0.2674 0.2434 0.1945 0.0873 0.2768 nbr_children 0.2560 -0.4477 0.1238 -0.0895 -0.0739 -0.5642 0.0898 separated 0.3030 0.0692 0.0545 -0.0666 -0.0796 -0.5089 -0.6425 single -0.2902 0.7648 -0.3004 -0.2010 -0.2120 0.2527 0.0360 svacct 0.4365 0.1616 -0.2592 -0.1705 0.6336 -0.1071 0.0318 years_with_bank 0.0362 -0.0966 0.2120 0.0543 -0.0668 0.5507 -0.5299 84 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Factor Analysis Variance Table 21: Factor Variance to Total Variance Ratio .665 Table 22: Variance Explained By Factors Factor Variance Percent of Total Variance Cumulative Percent Condition Indices Factor 1 4.2920 20.4383 20.4383 1.0000 Factor 2 2.4972 11.8914 32.3297 1.3110 Factor 3 1.8438 8.7800 41.1097 1.5257 Factor 4 1.5977 7.6082 48.7179 1.6390 Factor 5 1.4462 6.8869 55.6048 1.7227 Factor 6 1.2544 5.9735 61.5782 1.8497 Factor 7 1.0413 4.9586 66.5369 2.0302 Table 23: Difference Mean Standard Deviation Minimum Maximum 0.0570 0.0866 0.0000 0.7909 Table 24: Prime Factor Variables Factor 1 Factor 2 Factor 3 Factor 4 Factor 5 Factor 6 Factor 7 cc_rev married avg_sv_tran_amt avg_cc_tran_cnt svacct nbr_children separated avg_ck_tran_amt single avg_sv_tran_cnt ckacct avg_ck_tran_cnt years_with_bank female avg_cc_bal ccacct avg_sv_bal * * * * income age * * * * * avg_ck_bal * * * * * * avg_cc_tran_amt * * * * * * Pattern Graph By default, the first twelve variables input to the Factor Analysis, and the first two factors generated, are displayed on the Factor Patterns graph: Teradata Warehouse Miner User Guide - Volume 3 85 Chapter 1: Analytic Algorithms Linear Regression Scree Plot On the scree plot, all possible factors are shown. In this case, only factors with an eigenvalue greater than 1 were generated by the Factor Analysis: Figure 54: Factor Analysis Tutorial: Scree Plot Linear Regression Overview Linear regression is one of the oldest and most fundamental types of analysis in statistics. The British scientist Sir Francis Galton originally developed it in the latter part of the 19th century. The term “regression” derives from the nature of his original study in which he found that the children of both tall and short parents tend to “revert” or “regress” toward average heights. [Neter] It has also been associated with the work of Gauss and Legendre who used linear models in working with astronomical data. Linear regression is thought of today as a special case of generalized linear models, which also includes models such as logit models (logistic regression), log-linear models and multinomial response models. [McCullagh] Why build a linear regression model? It is after all one of the simplest types of models that can be built. Why not start out with a more sophisticated model such as a decision tree or a neural network model? One reason is that if a simpler model will suffice, it is better than an unnecessarily complex model. Another reason is to learn about the relationships between a set of observed variables. Is there in fact a linear relationship between each of the observed variables and the variable to predict? Which variables help in predicting the target dependent variable? If a linear relationship does not exist, is there another type of relationship that does? 86 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression By transforming a variable, say by taking its exponent or log or perhaps squaring it, and then building a linear regression model, these relationships can hopefully be seen. In some cases, it may even be possible to create an essentially non-linear model using linear regression by transforming the data first. In fact, one of the many sophisticated forms of regression, called piecewise linear regression, was designed specifically to build nonlinear models of nonlinear phenomena. Finally, in spite of being a relatively simple type of model, there is a rich set of statistics available to explore the nature of any linear regression model built. Multiple Linear Regression Multiple linear regression analysis attempts to predict, or estimate, the value of a dependent variable as a linear combination of independent variables, usually with a constant term included. That is, it attempts to find the b-coefficients in the following equation in order to best predict the value of the dependent variable y based on the independent variables x1 to xn. ) y = b0 + b1 x1 + + bn xn The best values of the coefficients are defined to be the values that minimize the sum of squared error values: y ) y – 2 over all the observations. ) Note that this requires that the actual value of y be known for each observation, in order to contrast it with the predicted value y . This technique is called “least-squared errors.” It turns out that the b-coefficient values to minimize the sum of squared errors can be solved using a little calculus and linear algebra. It is worth spending just a little more effort in describing this technique in order to explain how Teradata Warehouse Miner performs linear regression analysis. It also introduces the concept of a cross-products matrix and its relatives the covariance matrix and the correlation matrix that are so important in multivariate statistical analysis. In order to minimize the sum of squared errors, the equation for the sum of squared errors is expanded using the equation for the estimated y value, and then the partial derivatives of this equation with respect to each b-coefficient are derived and set equal to 0. (This is done in order to find the minimum with respect to all of the coefficient values). This leads to n simultaneous equations in n unknowns, which are commonly referred to as the normal equations. For example: 1 1 b0 + 1 x1 b1 + 1 x2 b2 = 1 y x1 1 b0 + x1 b1 + x1 x2 b2 = x1 y 2 x2 1 b0 + x2 x1 b1 + x2 b2 = 2 Teradata Warehouse Miner User Guide - Volume 3 x2 y 87 Chapter 1: Analytic Algorithms Linear Regression The equations above have been presented in a way that gives a hint to how they can be solved using matrix algebra, i.e. by first computing the extended Sum-of-Squares-and-CrossProducts (SSCP) matrix for the constant 1 and the variables x1, x2 and y. By doing this one gets all of the terms in the equation. Teradata Warehouse Miner offers the Build Matrix function to build the SSCP matrix directly in the Teradata database using generated SQL. The linear regression module then reads this matrix from metadata results tables and performs the necessary calculations to solve for the least-squares b-coefficients. Therefore, that part of constructing a linear regression algorithm that requires access to the detail data is simply the building of the extended SSCP matrix (i.e. include the constant 1 as the first variable), and the rest is calculated on the client machine. There is however much more to linear regression analysis than building a model, i.e. calculating the least-squares values of the b-coefficients. Other aspects such as model diagnostics, stepwise model selection and scoring are described below. Model Diagnostics One of the advantages in using a statistical modeling technique such as linear regression (as opposed to a machine learning technique, for example) is the ability to compute rigorous, well-understood measurements of the effectiveness of the model. Most of these measurements are based upon a huge body of work in the areas of probability and probability theory. Goodness of fit ) Several model diagnostics are provided to give an assessment of the effectiveness of the overall model. One of these is called the residual sums of squares or sum of squared errors RSS, which is simply the sum of the squared differences between the dependent variable y estimated by the model and the actual value of y, over all of the rows: y – y ) RSS = 2 Now suppose a similar measure was created based on a naive estimate of y, namely the mean value y : TSS = y – y 2 often called the total sums of squares about the mean. Then, a measure of the improvement of the fit given by the linear regression model is given by: TSS – RSS 2 R = ---------------------------TSS This is called the squared multiple correlation coefficient R2, which has a value between 0 and 1, with 1 indicating the maximum improvement in fit over estimating y naively with the mean value of y. The multiple correlation coefficient R is actually the correlation between the real y values and the values predicted based on the independent x variables, sometimes written R y x 1 x 2 x n , which is calculated here simply as the positive square root of the R2 88 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression value. A variation of this measure adjusted for the number of observations and independent variables in the model is given by the adjusted R2 value: 2 n–1 2 R = 1 – --------------------- 1 – R n–p–1 where n is the number of observations and p is the number of independent variables (substitute n-p in the denominator if there is no constant term). The numerator in the equation for R2, namely TSS - RSS, is sometimes called the due-toregression sums of squares or DRS. Another way of looking at this is that the total unexplained variation about the mean TSS is equal to the variation due to regression DRS plus the unexplained residual variation RSS. This leads to an equation sometimes known as the fundamental equation of regression analysis: = y 2 – y + y – y ) 2 ) y – y 2 Which is the same as saying that TSS = DRS + RSS. From these values a statistical test called an F-test can be made to determine if all the x variables taken together explain a significant amount of variation in y. This test is carried out on the F-ratio given by: meanDRS F = -------------------------meanRSS The values meanDRS and meanRSS are calculated by dividing DRS and RSS by their respective degrees of freedom (p for DRS and n-p-1 for RSS). Standard errors and confidence intervals Measurements are made of the standard deviation of the sampling distribution of each bcoefficient value, and from this, estimates of a confidence interval for each of the coefficients are made. For example, if one of the coefficients has a value of 6, and a 95% confidence interval of 5 to 7, it can be said that the true population coefficient is contained in this interval, with a confidence coefficient of 95%. In other words, if repeated samples were taken of the same size from the population, then 95% of the intervals like the one constructed here, would contain the true value for the population coefficient. Another set of useful statistics is calculated as the ratio of each b-coefficient value to its standard error. This statistic is sometimes called a T-statistic or Wald statistic. Along with its associated t-distribution probability value, it can be used to assess the statistical significance of this term in the model. Standardized coefficients The least-squares estimates of the b-coefficients are converted to so-called beta-coefficients or standardized coefficients to give a model in terms of the z-scores of the independent variables. That is, the entire model is recast to use standardized values of the variables and the coefficients are recomputed accordingly. Standardized values cast each variable into units Teradata Warehouse Miner User Guide - Volume 3 89 Chapter 1: Analytic Algorithms Linear Regression measuring the number of standard deviations away from the mean value for that variable. The advantage of doing this is that the values of the coefficients are scaled equivalently so that their relative importance in the model can be more easily seen. Otherwise the coefficient for a variable such as income would be difficult to compare to a variable such as age or the number of years an account has been open. Incremental R-squared It is possible to calculate the value R2 incrementally by considering the cumulative contributions of x variables added to the model one at a time, namely R y x 1 , R y x1 x2 R y x1 x2 xn . These are called incremental R2 values, and they give a measure of how much the addition of each x variable contributes to explaining the variation in y in the observations. This points out the fact that the order in which the independent x variables are specified in creating the model is important. Multiple Correlation Coefficients Another measure that can be computed for each independent variable in the model is the squared multiple correlation coefficient with respect to the other independent variables in the model taken together. These values range from 0 to1 with 0 indicating a lack of correlation and 1 indicating the maximum correlation. Multiple correlation coefficients are sometimes presented in related forms such as variance inflation factors or tolerances. A variance inflation factor is given by the formula: 1 V k -----------------2 1 – Rk Where Vk is the variance inflation factor and Rk2 is the squared multiple correlation coefficient for the kth independent variable. Tolerance is given by the formula Tk = 1 - Rk2, where Tk is the tolerance of the kth independent variable and Rk2 is as before. These values may be of limited value as indicators of possible collinearity or near dependencies among variables in the case of high correlation values, but the absence of high correlation values does not necessarily indicate the absence of collinearity problems. Further, multiple correlation coefficients are unable to distinguish between several near dependencies should they exist. The reader is referred to [Belsley, Kuh and Welsch] for more information on collinearity diagnostics, as well as to the upcoming section on the subject. Data Quality Reports A variety of data quality reports are available with the Teradata Warehouse Miner Linear Regression algorithm. Reports include: 90 1 Constant Variables 2 Variable Statistics 3 Detailed Collinearity Diagnostics • Eigenvalues of Unit Scaled X'X • Condition Indices • Variance Proportions Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression 4 Near Dependency Constant Variables Before attempting to build a model the algorithm checks to see if any variables in the model have a constant value. This check is based on the standard deviation values derived from the SSCP matrix input to the algorithm. If a variable with a constant value, i.e. a standard deviation of zero, is detected, the algorithm stops and notifies the user while producing a Constant Variables Table report. After reading this report, the user may then remove the variables in the report from the model and execute the algorithm again. It is possible that a variable may appear in the Constant Variables Table report that does not actually have a constant value in the data. This can happen when a column has extremely large values that are close together in value. In this case the standard deviation will appear to be zero due to precision loss and will be rejected as a constant column. The remedy for this is to re-scale the values in the column prior to building a matrix or doing the analysis. The ZScore or the Rescale transformation functions may be used for this purpose. Variable Statistics The user may optionally request that a Variables Statistics Report be provided, giving the mean value and standard deviation of each variable in the model based on the SSCP matrix provided as input. Detailed Collinearity Diagnostics One of the conditions that can lead to a poor linear regression model is when the independent variables in the model are not independent of each other, that is, when they are collinear (highly correlated) with one another. Collinearity can be loosely defined as a condition where one variable is nearly a linear combination of one or more other variables, sometimes also called a near dependency. This leads to an ill conditioned matrix of variables. Teradata Warehouse Miner provides an optional Detailed Collinearity Diagnostics report using a specialized technique described in [Belsley, Kuh and Welsch]. This technique involves performing a singular value decomposition of the independent x variables in the model in order to measure collinearity. The analysis proceeds roughly as follows. In order to put all variables on an equal footing, the data is scaled so that each variable adds up to 1 when summed over all the observations or rows. In order to calculate the singular values of X (the rows of X are the observations), the mathematically equivalent square root of the eigenvalues of XTX are computed instead for practical reasons. The condition index of each eigenvalue is calculated as the square root of the ratio of the largest eigenvalue to the given eigenvalue, a value always 1 or greater. The variance decomposition of these eigenvalues is computed using the eigenvalues together with the eigenvectors associated with them. The result is a matrix giving, for each variable, the proportion of variance associated with each eigenvalue. Large condition indices indicate a probable near dependency. A value of 10 may indicate a weak dependency, values of 15 to 30 may be considered a borderline dependency, above 30 worth investigating further, and above 100, a potentially damaging collinearity. As a rule of thumb, an eigenvalue with a condition index greater than 30 and an associated variance proportion of greater than 50% with two or more model variables implies that a collinearity Teradata Warehouse Miner User Guide - Volume 3 91 Chapter 1: Analytic Algorithms Linear Regression problem exists. (The somewhat subjective conclusions described here and the experiments they are based on are described in detail in [Belsley, Kuh and Welsch]). An example of the Detailed Collinearity Diagnostics report is given below. Table 25: Eigenvalues of Unit Scaled X'X Factor 1 5.2029 Factor 2 .8393 Factor 3 .5754 Factor 4 .3764 Factor 5 4.1612E-03 Factor 6 1.8793E-03 Factor 7 2.3118E-08 Table 26: Condition Indices Factor 1 1 Factor 2 2.4898 Factor 3 3.007 Factor 4 3.718 Factor 5 35.3599 Factor 6 52.6169 Factor 7 15001.8594 Table 27: Variable Name Factor 1 Factor 2 Factor 3 Factor 4 Factor 5 Factor 6 Factor 7 CONSTANT 1.3353E-09 1.0295E-08 1.3781E-09 1.6797E-08 1.1363E-11 2.1981E-07 1 cust_id 1.3354E-09 1.0296E-08 1.3782E-09 1.6799E-08 1.1666E-11 2.2068E-07 1 income 2.3079E-04 1.8209E-03 1.6879E-03 1.1292E-03 .9951 4.4773E-06 1.2957E-05 age 1.0691E-04 1.9339E-04 9.321E-05 1.7896E-03 1.56E-05 .9963 1.4515E-03 children 2.9943E-03 4.4958E-02 .2361 1.6499E-03 3.6043E-04 .713 9.1708E-04 combo1 2.3088E-04 1.8703E-03 1.6658E-03 1.1339E-03 .995 1.0973E-04 2.3525E-05 combo2 1.4002E-04 3.1477E-05 4.4942E-05 5.0407E-03 4.7784E-06 .9935 1.2583E-03 92 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression Near Dependency In addition to or in place of the Detailed Collinearity Diagnostics report, the user may optionally request a Near Dependency report based on the automated application of the specialized criteria used in the aforementioned report. Requesting the Near Dependency report greatly simplifies the search for collinear variables or near dependencies in the data. The user may specify the threshold value for the condition index (by default 30) and the variance proportion (by default 0.5) such that a near dependency is reported. That is, if two or more variables have a variance proportion greater than the variance proportion threshold, for a condition index with value greater than the condition index threshold, the variables involved in the near dependency are reported along with their variance proportions, their means and their standard deviations. Near dependencies are reported in descending order based on their condition index value, and variables contributing to a near dependency are reported in descending order based on their variance proportion. The following is an example of a Near Dependency report. Table 28: Near Dependency report (example) Variable Name Factor Condition Index Variance Proportion Mean Standard Deviation CONSTANT 7 15001.8594 1 * * cust_id 7 15001.8594 1 1362987.891 293.5012 age 6 52.6169 .9963 33.744 22.3731 combo2 6 52.6169 .9935 25.733 23.4274 children 6 52.6169 .713 .534 1.0029 income 5 35.3599 .9951 16978.026 21586.8442 combo1 5 35.3599 .995 33654.602 43110.862 Stepwise Linear Regression Automated stepwise regression analysis is a technique to aid in regression model selection. That is, it helps in deciding which independent variables to include in a regression model. If there are only two or three independent variables under consideration, one could try all possible models. But since there are 2k - 1 models that can be built from k variables, this quickly becomes impractical as the number of variables increases (32 variables yield more than 4 billion models!). The automated stepwise procedures described below can provide insight into the variables that should be included in a regression model. It is not recommended that stepwise procedures be the sole deciding factor in the makeup of a model. For one thing, these techniques are not guaranteed to produce the best results. And sometimes, variables should be included because of certain descriptive or intuitive qualities, or excluded for subjective reasons. Therefore an element of human decision-making is recommended to produce a model with useful business application. Teradata Warehouse Miner User Guide - Volume 3 93 Chapter 1: Analytic Algorithms Linear Regression Forward-Only Stepwise Linear Regression The forward only procedure consists solely of forward steps as described below, starting without any independent x variables in the model. Forward steps are continued until no variables can be added to the model. Forward Stepwise Linear Regression The forward stepwise procedure is a combination of the forward and backward steps described below, starting without any independent x variables in the model. One forward step is followed by one backward step, and these single forward and backward steps are alternated until no variables can be added or removed. Backward-Only Stepwise Linear Regression The backward only procedure consists solely of backward steps as described below, starting with all of the independent x variables in the model. Backward steps are continued until no variables can be removed from the model. Backward Stepwise Linear Regression The backward stepwise procedure is a combination of the backward and forward steps as described below, starting with all of the independent x variables in the model. One backward step is followed by one forward step, and these single backward and forward steps are alternated until no variables can be added or removed. Stepwise Linear Regression - Forward Step Each forward step seeks to add the independent variable x that will best contribute to explaining the variance in the dependent variable y. In order to do this a quantity called the partial F statistic must be computed for each xi variable that can be added to the model. A quantity called the extra sums of squares is first calculated as follows: ESS = “DRS with xi” “DRS w/o xi”, where DRS is the Regression Sums of squares or “due-to-regression sums of squares”. Then, the partial F statistic is given by f(xi) = ESS(xi) / meanRSS(xi) where meanRSS is the Residual Mean Square. Each forward step then consists of adding the variable with the largest partial F statistic providing it is greater than the criterion to enter value. An equivalent alternative to using the partial F statistic is to use the probability or P-value associated with the T-statistic mentioned earlier under model diagnostics. The t statistic is the ratio of the b-coefficient to its standard error. Teradata Warehouse Miner offers both alternatives as an option. When the P-value is used, a forward step consists of adding the variable with the smallest P-value providing it is less than the criterion to enter. In this case, if more than one variable has a P-value of 0, the variable with the largest F statistic is entered. Stepwise Linear Regression - Backward Step Each backward step seeks to remove the independent variable xi that least contributes to explaining the variance in the dependent variable y. The partial F statistic is calculated for each independent x variable in the model. If the smallest value is less than the criterion to remove, it is removed. As with forward steps, an option is provided to use the probability or P-value associated with the T-statistic, that is, the ratio of the b-coefficient to its standard error. In this case all the 94 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression probabilities or P-values are calculated for the variables currently in the model at one time, and the one with the largest P-value is removed if it is greater than the criterion to remove. Linear Regression and Missing Data Null values for columns in a linear regression analysis can adversely affect results. It is recommended that the listwise deletion option be used when building the input matrix with the Build Matrix function. This ensures that any row for which one of the columns is null will be left out of the matrix computations completely. Another strategy is to use the Recoding transformation function to build a new column, substituting a fixed known value for null values. Yet another option is to use one of the analytic algorithms in Teradata Warehouse Miner to estimate replacement values for null values. This technique is often called missing value imputation. Initiate a Linear Regression Function Use the following procedure to initiate a new Linear Regression analysis in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 55: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Analytics under Categories and then under Analyses double-click on Linear Regression: Teradata Warehouse Miner User Guide - Volume 3 95 Chapter 1: Analytic Algorithms Linear Regression Figure 56: Add New Analysis dialog 3 This will bring up the Linear Regression dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Linear Regression - INPUT - Data Selection On the Linear Regression dialog click on INPUT and then click on data selection: Figure 57: Linear Regression > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input, Table, Matrix or Analysis. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. (In this case a matrix will be dynamically built and discarded when the algorithm completes execution). By selecting the Input Source Matrix the user may can select from available matrices created by the Build Matrix function. This has the advantage that the matrix selected for input is available for further analysis after completion of the algorithm, perhaps selecting a different subset of columns from the matrix. By selecting the Input Source Analysis the user can select directly from the output of another analysis of qualifying type in the current project. (In this case a matrix will be dynamically built and discarded when the algorithm completes execution). Analyses that 96 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 Select Columns From One Table • Available Databases (only for Input Source equal to Table) — All the databases which are available for the Linear Regression analysis. • Available Matrices (only for Input Source equal to Matrix) — When the Input source is Matrix, a matrix must first be built with the Build Matrix function before linear regression can be performed. Select the matrix that summarizes the data to be analyzed. (The matrix must have been built with more rows than selected columns or the Linear Regression analysis will produce a singular matrix, causing a failure). • Available Analyses (only for Input Source equal to Analysis) — All the analyses that are available for the Linear Regression analysis. • Available Tables (only for Input Source equal to Table or Analysis) — All the tables that are available for the Linear Regression analysis. • Available Columns — All the columns that are available for the Linear Regression analysis. • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can either insert columns as Dependent or Independent columns. Make sure you have the correct portion of the window highlighted. The Dependent variable column is the column whose value is being predicted by the linear regression model. The algorithm requires that the Dependent and Independent columns must be of numeric type (or contain numbers in character format). Linear Regression - INPUT - Analysis Parameters On the Linear Regression dialog click on INPUT and then click on analysis parameters: Figure 58: Linear Regression > Input > Analysis Parameters On this screen select: • Regression Options Teradata Warehouse Miner User Guide - Volume 3 97 Chapter 1: Analytic Algorithms Linear Regression • Include Constant — This option specifies that the linear regression model should include a constant term. With a constant, the linear equation can be thought of as: ŷ = b 0 + b 1 x 1 + + b n x n Without a constant, the equation changes to: ŷ = b 1 x 1 + + b n x n • Stepwise Options — The Linear Regression analysis can use the stepwise technique to automatically determine a variable’s importance (or lack there of) to a particular model. If selected, the algorithm is performed repeatedly with various combinations of independent variable columns to attempt to arrive at a final “best” model. The stepwise options are: Step Direction — (Selecting “None” turns off the Stepwise option). • • Forward Only — Option to add qualifying independent variables one at a time. • Forward — Option for independent variables being added one at a time to an empty model, possibly removing a variable after a variable is added. • Backward Only — Option to remove independent variables one at a time. • Backward — Option for variables being removed from an initial model containing all of the independent variables, possibly adding a variable after a variable is removed. Step Method • F Statistic — Option to choose the partial F test statistic (F statistic) as the basis for adding or removing model variables. • P-value — Option to choose the probability associated with the T-statistic (Pvalue) as the basis for adding or removing model variables. • Criterion to Enter • Criterion to Remove — If the step method is to use the F statistic, then an independent variable is only added to the model if the F statistic is greater than the criterion to enter and removed if it is less than the criterion to remove. When the F statistic is used, the default for each is 3.84. If the step method is to use the P-value, then an independent variable is added to the model if the P-value is less than the criterion to enter and removed if it is greater than the criterion to remove. When the P-value is used, the default for each is 0.05. The default F statistic criteria of 3.84 corresponds to a P-value of 0.05. These default values are provided with the assumption that the input variables are somewhat correlated. If this is not the case, a lower F statistic or higher P-value criteria can be used. Also, a higher F statistic or lower P value can be specified if more stringent criteria are desired for including variables in a model. • Report Options — Statistical diagnostics can be taken on each variable during the execution of the Linear Regression Analysis. These diagnostics include: • 98 Variable Statistics — This report gives the mean value and standard deviation of each variable in the model based on the SSCP matrix provided as input. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression • Near Dependency — This report lists collinear variables or near dependencies in the data based on the SSCP matrix provided as input. Condition Index Threshold — Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The one that involves this parameter is the occurrence of a large condition index value associated with a specially constructed principal factor. If a factor has a condition index greater than this parameter’s value, it is a candidate for the Near Dependency report. A default value of 30 is used as a rule of thumb. Variance Proportion Threshold — Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The one that involves this parameter is when two or more variables have a variance proportion greater than this threshold value for a factor with a high condition index. Another way of saying this is that a ‘suspect’ factor accounts for a high proportion of the variance of two or more variables. This parameter defines what a high proportion of variance is. A default value of 0.5 is used as a rule of thumb. • Detailed Collinearity Diagnostics — This report provides the details behind the Near Dependency report, consisting of the “Eigenvalues of Unit Scaled X’X”, “Condition Indices” and “Variance Proportions” tables. Linear Regression - OUTPUT On the Linear Regression dialog click on OUTPUT: Figure 59: Linear Regression > OUTPUT On this screen select: • Store the variables table of this analysis in the database — Check this box to store the model variables table of this analysis in in the database. • Database Name — The name of the database to create the output table in. • Output Table Name — The name of the output table. • Advertise Output — The Advertise Output option "advertises" output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. Teradata Warehouse Miner User Guide - Volume 3 99 Chapter 1: Analytic Algorithms Linear Regression By way of an example, the tutorial example creates the following output table: Table 29: Upper Increment Standard al RCoefficient Squared SqMultiCo rrCoef(1Tolerance) 0.1694 1.6294 0.0331 0.8787 0.1312 0.0417 0.0111 0.5771 0.0263 0.8794 0.0168 -2.7887 0.0054 -1.3198 -0.2293 -0.036 0.8779 0.0207 0.0004 -41.3942 0 -0.0182 -0.0166 -0.6382 0.7556 0.3135 10.2793 0.8162 12.5947 0 8.677 11.8815 0.1703 0.8732 0.1073 income 0.0005 0 24.5414 0 0.0005 0.0005 0.3777 0.8462 0.311 married -4.3056 0.8039 -5.3558 0 -5.8838 -2.7273 -0.0718 0.8766 0.0933 0.9749 -6.6301 0 -8.378 -4.55 0 0 Column Name B Standard Coefficient Error T Statistic P-Value Lower nbr_ children 0.8994 0.3718 2.4187 0.0158 years_ 0.2941 with_bank 0.1441 2.0404 avg_sv_ tran_cnt -0.7746 0.2777 avg_cc_ bal -0.0174 ckacct (Constant) -6.464 If Database Name is twm_results and Output Table Name is test, the output table is defined as: CREATE SET TABLE twm_results.test2 ( "Column Name" VARCHAR(30) CHARACTER SET UNICODE NOT CASESPECIFIC, "B Coefficient" FLOAT, "Standard Error" FLOAT, "T Statistic" FLOAT, "P-Value" FLOAT, "Lower" FLOAT, "Upper" FLOAT, "Standard Coefficient" FLOAT, "Incremental R-Squared" FLOAT, "SqMultiCorrCoef(1-Tolerance)" FLOAT) UNIQUE PRIMARY INDEX ( "Column Name" ); Run the Linear Regression After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard 100 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression Results - Linear Regression The results of running the Teradata Warehouse Miner Linear Regression analysis include a variety of statistical reports on the individual variables and generated model as well as barcharts displaying coefficients and T-statistics. All of these results are outlined below. Linear Regression - RESULTS On the Linear Regression dialog, click on RESULTS (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed) to view results. Result options are as follows: Linear Regression Reports Data Quality Reports • Variable Statistics — If selected on the Results Options tab, this report gives the mean value and standard deviation of each variable in the model based on the SSCP matrix provided as input. • Near Dependency — If selected on the Results Options tab, this report lists collinear variables or near dependencies in the data based on the SSCP matrix provided as input. Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The first is the occurrence of a large condition index value associated with a specially constructed principal factor. If a factor has a condition index greater than the parameter specified on the Results Option tab, it is a candidate for the Near Dependency report. The other is when two or more variables have a variance proportion greater than a threshold value for a factor with a high condition index. Another way of saying this is that a ‘suspect’ factor accounts for a high proportion of the variance of two or more variables. The parameter to defines what a high proportion of variance is also set on the Results Option tab. A default value of 0.5. • Detailed Collinearity Diagnostics — If selected on the Results Options tab, this report provides the details behind the Near Dependency report, consisting of the following tables. • Eigenvalues of Unit Scaled X'X — Report of the eigenvalues of all variables scaled so that each variable adds up to 1 when summed over all the observations or rows. In order to calculate the singular values of X (the rows of X are the observations), the mathematically equivalent square root of the eigenvalues of XTX are computed instead for practical reasons. • Condition Indices — The condition index of each eigenvalue, calculated as the square root of the ratio of the largest eigenvalue to the given eigenvalue, a value always 1 or greater. • Variance Proportions — The variance decomposition of these eigenvalues is computed using the eigenvalues together with the eigenvectors associated with them. The result is a matrix giving, for each variable, the proportion of variance associated with each eigenvalue. Linear Regression Step N (Stepwise-only) • Linear Regression Model Assessment Teradata Warehouse Miner User Guide - Volume 3 101 Chapter 1: Analytic Algorithms Linear Regression • Squared Multiple Correlation Coefficient (R-squared) — This is the same value calculated for the Linear Regression report, but it is calculated here for the model as it stands at this step. The closer to 1 its value is, the more effective the model. • Standard Error of Estimate — This is the same value calculated for the Linear Regression report, but it is calculated here for the model as it stands at this step. • In Report — This report contains the same fields as the Variables in Model report (described below) with the addition of the following field. • F Stat — F Stat is the partial F statistic for this variable in the model, which may be used to decide its inclusion in the model. A quantity called the extra sums of squares is first calculated as follows: ESS = “DRS with x” - “DRS w/o”, where DRS is the Regression Sums of squares or “due-to-regression sums of squares”. Then the partial F statistic is given by F(xi) = ESS(xi) / meanRSS(xi), where meanRSS is the Residual Mean Square. • Out Report • Independent Variable — This is an independent variable not included in the model at this step. • P-Value — This is the probability associated with the T-statistic associated with each variable not in, or excluded from, the model, as described for the Variables in Model report as T Stat and P-Value. (Note that it is not the P-Value associated with F Stat). When the P-Value is used for step decisions, a forward step consists of adding the variable with the smallest P-value providing it is less than the criterion to enter. For backward steps, all the probabilities or P-values are calculated for the variables currently in the model at one time, and the one with the largest P-value is removed if it is greater than the criterion to remove. • F Stat — F Stat is the partial F statistic for this variable in the model, which may be used to decide its inclusion in the model. A quantity called the extra sums of squares is first calculated as follows: ESS = “DRS with xi” - “DRS w/o xi”, where DRS is the Regression Sums of squares or “due-to-regression sums of squares”. Then the partial F statistic is given by F(xi) = ESS(xi) / meanRSS(xi), where meanRSS is the Residual Mean Square. • Partial Correlation — The partial correlation coefficient for a variable not in the model is based on the square root of a measure called the coefficient of partial determination, which represents the marginal contribution of the variable to a model that doesn’t include the variable. (Here, contribution to the model means reduction in the unexplained variation of the dependent variable). The formula for the partial correlation of the ith independent variable in the linear regression model built from all the independent variables is given by: Ri = DRS – NDRS ----------------------------------RSS where DRS is the Regression Sums of squares for the model including those variables currently in the model, NDRS is the Regression Sums of squares for the current model 102 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression without the ith variable, and RSS is the Residual Sums of squares for the current model. Linear Regression Model • Total Observations — This is the number of rows originally summarized in the SSCP matrix that the linear regression analysis is based on. The number of observations reflects the row count after any rows were eliminated by listwise deletion (recommended) when the matrix was built. • Total Sums of squares — The so-called Total Sums of squares is given by the 2 equation TSS = y – y where y is the dependent variable that is being predicted and y is its mean value. The Total Sums of squares is sometimes also called the total sums of squares about the mean. Of particular interest is its relation to the “due-to-regression sums of squares” and the “residual sums of squares” given by TSS = DRS + RSS. This is a shorthand form of what is sometimes known as the fundamental equation of regression analysis: y – y 2 = ŷ – y 2 = y – ŷ 2 where y is the dependent variable, y is its mean value and ŷ is its predicted value. • Multiple Correlation Coefficient (R) — The multiple correlation coefficient R is the correlation between the real dependent variable y values and the values predicted based on the independent x variables, sometimes written R y x1 x2 xn , which is calculated in Teradata Warehouse Miner simply as the positive square root of the Squared Multiple Correlation Coefficient (R2) value. • Squared Multiple Correlation Coefficient (R-squared) — The squared multiple correlation coefficient R2 is a measure of the improvement of the fit given by the linear regression model over estimating the dependent variable y naïvely with the mean value of y. It is given by: TSS – RSS 2 R = ---------------------------TSS where TSS is the Total Sums of squares and RSS is the Residual Sums of squares. It has a value between 0 and 1, with 1 indicating the maximum improvement in fit over estimating y naïvely with the mean value of y. • Adjusted R-squared — The adjusted R2 value is a variation of the Squared Multiple Correlation Coefficient (R2) that has been adjusted for the number of observations and independent variables in the model. Its formula is given by: n–1 2 2 R = 1 – --------------------- 1 – R n–p–1 where n is the number of observations and p is the number of independent variables (substitute n-p in the denominator if there is no constant term). • Standard Error of Estimate — The standard error of estimate is calculated as the square root of the average squared residual value over all the observations, i.e. Teradata Warehouse Miner User Guide - Volume 3 103 Chapter 1: Analytic Algorithms Linear Regression y – ŷ -------------------------- 2 n–p–1 where y is the actual value of the dependent variable, ŷ is its predicted value, n is the number of observations, and p is the number of independent variables (substitute n-p in the denominator if there is no constant term). • Regression Sums of squares — This is the “due-to-regression sums of squares” or DRS referred to in the description of the Total Sums of squares, where it is pointed out that TSS = DRS + RSS. It is also the middle term in what is sometimes known as the fundamental equation of regression analysis: y – y 2 = ŷ – y 2 = y – ŷ 2 where y is the dependent variable, is its mean value and is its predicted value. • Regression Degrees of Freedom — The Regression Degrees of Freedom is equal to the number of independent variables in the linear regression model. It is used in the calculation of the Regression Mean-Square. • Regression Mean-Square — The Regression Mean-Square is simply the Regression Sums of squares divided by the Regression Degrees of Freedom. This value is also the numerator in the calculation of the Regression F Ratio. • Regression F Ratio — A statistical test called an F-test is made to determine if all the independent x variables taken together explain a statistically significant amount of variation in the dependent variable y. This test is carried out on the F-ratio given by meanDRS F = -------------------------meanRSS where meanDRS is the Regression Mean-Square and meanRSS is the Residual MeanSquare. A large value of the F Ratio means that the model as a whole is statistically significant. (The easiest way to assess the significance of this term in the model is to check if the associated Regression P-Value is less than 0.05. However, the critical value of the F Ratio could be looked up in an F distribution table. This value is very roughly in the range of 1 to 3, depending on the number of observations and variables). • Regression P-value — This is the probability or P-value associated with the statistical test on the Regression F Ratio. This statistical F-test is made to determine if all the independent x variables taken together explain a statistically significant amount of variation in the dependent variable y. A value close to 0 indicates that they do. (The hypothesis being tested or null hypothesis is that the coefficients in the model are all zero except the constant term, i.e. all the corresponding independent variables together contribute nothing to the model. The P-value in this case is the probability that the null hypothesis is true and the given F statistic has the value it has or smaller. A right tail test on the F distribution is performed with a 5% significance level used by convention. If the P-value is less than the significance level, i.e. less than 0.05, the null hypothesis should be rejected, i.e. the coefficients taken together are significant and not all 0). 104 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression • Residual Sums of squares — The residual sums of squares or sum of squared errors RSS is simply the sum of the squared differences between the dependent variable estimated by the model and the actual value of y, over all of the rows: RSS = y – ŷ 2 • Residual Degrees of Freedom — The Residual Degrees of Freedom is given by n-p-1 where n is the number of observations and p is the number of independent variables (or np if there is no constant term). It is used in the calculation of the Residual Mean-Square. • Residual Mean-Square — The Residual Mean-Square is simply the Residual Sums of squares divided by the Residual Degrees of Freedom. This value is also the denominator in the calculation of the Regression F Ratio. Linear Regression Variables in Model Report • Dependent Variable — The dependent variable is the variable being predicted by the linear regression model. • Independent Variable — Each independent variable in the model is listed along with accompanying measures. Unless the user deselects the option Include Constant on the Regression Options tab of the input dialog, the first independent variable listed is CONSTANT, a fixed value representing the constant term in the linear regression model. • B Coefficient — Linear regression attempts to find the b-coefficients in the equation ŷ = b 0 + b 1 x 1 + b n x n in order to best predict the value of the dependent variable y based on the independent variables x1 to xn. The best values of the coefficients are defined to be the values that minimize the sum of squared error values y – ŷ 2 over all the observations. • Standard Error — This is the standard error of the B Coefficient term of the linear regression model, a measure of how accurate the B Coefficient term is over all the observations used to build the model. It is the basis for estimating a confidence interval for the B Coefficient value. • T Statistic — The T-statistic is the ratio of a B Coefficient value to its standard error (Std Error). Along with the associated t-distribution probability value or P-value, it can be used to assess the statistical significance of this term in the linear model. (The easiest way to assess the significance of this term in the model is to check if the Pvalue is less than 0.05. However, one could look up the critical T Stat value in a two-tailed T distribution table with probability .95 and degrees of freedom roughly the number of observations minus the number of variables. This would show that for all practical purposes, if the absolute value of T Stat is greater than 2 the model term is statistically significant). • P-value — This is the t-distribution probability value associated with the T-statistic (T Stat), that is, the ratio of the b-coefficient value to its standard error (Std Error). It can be used to assess the statistical significance of this term in the linear model. A value close to 0 implies statistical significance and means this term in the model is important. Teradata Warehouse Miner User Guide - Volume 3 105 Chapter 1: Analytic Algorithms Linear Regression (The hypothesis being tested or null hypothesis is that the coefficient in the model is actually zero, i.e. the corresponding independent variable contributes nothing to the model. The P-value in this case is the probability that the null hypothesis is true and the given T-statistic has the absolute value it has or smaller. A two-tailed test on the tdistribution is performed with a 5% significance level used by convention. If the P-value is less than the significance level, i.e. less than 0.05, the null hypothesis should be rejected, i.e. the coefficient is statistically significant and not 0). • Squared Multiple Correlation Coefficient (R-squared) — The Squared Multiple Correlation Coefficient (Rk2) is a measure of the correlation of this, the kth variable with respect to the other independent variables in the model taken together. (This measure should not be confused with the R2 measure of the same name that applies to the model taken as a whole). The value ranges from 0 to 1 with 0 indicating a lack of correlation and 1 indicating the maximum correlation. It is not calculated for the constant term in the model. Multiple correlation coefficients are sometimes presented in related forms such as variance inflation factors or tolerances. The variance inflation factor is given by the formula: 1 V k = --------------21 – Rk where Vk is the variance inflation factor and Rk2 is the squared multiple correlation coefficient for the kth independent variable. Tolerance is given by the 2 formula T k = 1 – R k where Tk is the tolerance of the kth independent variable and Rk2 is as before. (Refer to the section Multiple Correlation Coefficients for details on the limitations of using this measure to detect collinearity problems in the data). • Lower — Lower is the lower value in the confidence interval for this coefficient and is based on its standard error value. For example, if the coefficient has a value of 6 and a confidence interval of 5 to 7, it means that according to the normal error distribution assumptions of the model, there is a 95% probability that the true population value of the coefficient is actually between 5 and 7. • Upper — Upper is the upper value in the confidence interval for this coefficient based on its standard error value. For example, if the coefficient has a value of 6 and a confidence interval of 5 to 7, it means that according to the normal error distribution assumptions of the model, there is a 95% probability that the true population value of the coefficient is actually between 5 and 7. • Standard Coefficient — Standardized coefficients, sometimes called beta-coefficients, express the linear model in terms of the z-scores or standardized values of the independent variables. Standardized values cast each variable into units measuring the number of standard deviations away from the mean value for that variable. The advantage of examining standardized coefficients is that they are scaled equivalently, so that their relative importance in the model can be more easily seen. 106 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression • Incremental R-squared — It is possible to calculate the model’s Squared Multiple Correlation value incrementally by considering the cumulative contributions of x variables added to the model one at a time, namely R y x R y x x R y x x x . 1 1 2 1 2 n These are called Incremental R2 values, and they give a measure of how much the addition of each x variable contributes to explaining the variation in y in the observations. Linear Regression Graphs The Linear Regression Analysis can display the coefficients and/or T-statistics of the resultant model. Weights Graph This graph displays the relative magnitudes of the standardized coefficients and/or the Tstatistic associated with each standardized coefficient in the linear regression model. The sign, positive or negative, is portrayed by the colors red or blue respectively. The user may scroll to the left or right to see all the variables in the model. The T-statistic is the ratio of the coefficient value to its standard error, so the larger its value the more reliable the value of the coefficient is. The following options are available on the Graphics Options tab on the Linear Weights graph: • Graph Type — The following can be graphed by the Linear Weights Graph • T Statistic — Display the T Statistics on the bar chart. • Standardized Coefficient — Display the Standardized Coefficients on the bar chart. • Vertical Axis — The user may request multiple vertical axes in order to display separate coefficient values that are orders of magnitude different from the rest of the values. If the coefficients are of roughly the same magnitude, this option is grayed out. • Single — Display the Standardized Coefficients or T Statistics on single axis on the bar chart. • Multiple — Display the Standardized Coefficients or T Statistics on dual axes on the bar chart. Tutorial - Linear Regression Parameterize a Linear Regression Analysis as follows: • Available Matrices — Customer_Analysis_Matrix • Dependent Variable — cc_rev • Independent Variables • income — age • years_with_bank — nbr_children • female — single • married — separated • ccacct — ckacct • svacct — avg_cc_bal • avg_ck_bal — avg_sv_bal Teradata Warehouse Miner User Guide - Volume 3 107 Chapter 1: Analytic Algorithms Linear Regression • avg_cc_tran_amt — avg_cc_tran_cnt • avg_ck_tran_amt — avg_ck_tran_cnt • avg_sv_tran_amt — avg_sv_tran_cnt • Include Constant — Enabled • Step Direction — Forward • Step Method — F Statistic • Criterion to Enter — 3.84 • Criterion to Remove — 3.84 Run the analysis, and click on Results when it completes. For this example, the Linear Regression Analysis generated the following pages. A single click on each page name populates Results with the item. Table 30: Linear Regression Report Total Observations: 747 Total Sum of Squares: 6.69E5 Multiple Correlation Coefficient (R): 0.9378 Squared Multiple Correlation Coefficient (1-Tolerance): 0.8794 Adjusted R-Squared: 0.8783 Standard Error of Estimate: 1.04E1 Table 31: Regression vs. Residual Sum of Squares Degrees of Freedom Mean-Square F Ratio P-value Regression 5.88E5 7 8.40E4 769.8872 0.0000 Residual 8.06E4 739 1.09E2 N/A N/A Table 32: Execution Status 108 6/20/2004 2:07:28 PM Getting Matrix 6/20/2004 2:07:28 PM Stepwise Regression Running... 6/20/2004 2:07:28 PM Step 0 Complete 6/20/2004 2:07:28 PM Step 1 Complete 6/20/2004 2:07:28 PM Step 2 Complete 6/20/2004 2:07:28 PM Step 3 Complete 6/20/2004 2:07:28 PM Step 4 Complete 6/20/2004 2:07:28 PM Step 5 Complete Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression Table 32: Execution Status 6/20/2004 2:07:28 PM Step 6 Complete 6/20/2004 2:07:28 PM Step 7 Complete 6/20/2004 2:07:29 PM Creating Report Table 33: Variables Column Name B Standard Coefficient Error T Statistic P-value Lower Upper Standard Incremental Coefficient R Squared Multiple Correlation Coefficient (1Tolerance) (Constant) -6.4640 0.9749 -6.6301 0.0000 -8.3780 -4.5500 0.0000 0.0000 N/A avg_cc_bal -0.0174 0.0004 -41.3942 0.0000 -0.0182 -0.0166 -0.6382 0.7556 0.3135 income 0.0005 0.0000 24.5414 0.0000 0.0005 0.0005 0.3777 0.8462 0.3110 ckacct 10.2793 0.8162 12.5947 0.0000 8.6770 11.8815 0.1703 0.8732 0.1073 married -4.3056 0.8039 -5.3558 0.0000 -5.8838 -2.7273 -0.0718 0.8766 0.0933 avg_sv_ tran_cnt -0.7746 0.2777 -2.7887 0.0054 -1.3198 -0.2293 -0.0360 0.8779 0.0207 nbr_ children 0.8994 0.3718 2.4187 0.0158 0.1694 1.6294 0.0331 0.8787 0.1312 years_with_ 0.2941 bank 0.1441 2.0404 0.0417 0.0111 0.5771 0.0263 0.8794 0.0168 Step 0 Table 34: Out Independent Variable P-value F Stat age 0.0000 19.7680 avg_cc_bal 0.0000 2302.7983 avg_cc_tran_amt 0.0000 69.5480 avg_cc_tran_cnt 0.0000 185.3197 avg_ck_bal 0.0000 116.5094 avg_ck_tran_amt 0.0000 271.3578 avg_ck_tran_cnt 0.0002 13.9152 avg_sv_bal 0.0000 37.8598 Teradata Warehouse Miner User Guide - Volume 3 109 Chapter 1: Analytic Algorithms Linear Regression Table 34: Out Independent Variable P-value F Stat avg_sv_tran_amt 0.0000 76.1104 avg_sv_tran_cnt 0.7169 0.1316 ccacct 0.1754 1.8399 ckacct 0.0000 105.5843 female 0.5404 0.3751 income 0.0000 647.3239 married 0.8937 0.0179 nbr_children 0.0000 30.2315 separated 0.0000 28.7618 single 0.0000 17.1850 svacct 0.0001 15.7289 years_with_bank 0.1279 2.3235 Step 1 Table 35: Model Assessment Squared Multiple Correlation Coefficient (1-Tolerance) 0.7556 Standard Error of Estimate 14.8111 Table 36: Columns In (Part 1) Independent Variable B Coefficient Standard Error T Statistic P-value avg_cc_bal -0.0237 0.0005 -47.9875 0.0000 Independent Variable B Coefficient Lower Upper F Stat avg_cc_bal -0.0237 -0.0247 -0.0227 2302.7983 Table 37: Columns In (Part 2) 110 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression Table 38: Columns In (Part 3) Independent Variable B Coefficient Standard Coefficient Squared Multiple Correlation Coefficient (1-Tolerance) avg_cc_bal -0.0237 -0.8692 0.0000 Incremental R2 0.7556 Table 39: Columns Out Independent Variable P-value F Stat Partial Correlation age 0.0539 3.7287 0.0708 avg_cc_tran_amt 0.0000 27.4695 0.1921 avg_cc_tran_cnt 0.2346 1.4153 0.0436 avg_ck_bal 0.0000 17.1826 0.1520 avg_ck_tran_amt 0.0000 94.9295 0.3572 avg_ck_tran_cnt 0.4712 0.5198 0.0264 avg_sv_bal 0.0083 6.9952 0.0970 avg_sv_tran_amt 0.0164 5.7848 0.0882 avg_sv_tran_cnt 0.1314 2.2807 0.0554 ccacct 0.8211 0.0512 0.0083 ckacct 0.0000 41.3084 0.2356 female 0.3547 0.8575 0.0340 income 0.0000 438.7799 0.7680 married 0.4812 0.4967 0.0258 nbr_children 0.0000 30.4645 0.2024 separated 0.0004 12.8680 0.1315 single 0.0024 9.3169 0.1119 svacct 0.0862 2.9523 0.0630 years_with_bank 0.3407 0.9090 0.0350 Linear Weights Graph By default, the Linear Weights graph displays the relative magnitudes of the T-statistic associated with each coefficient in the linear regression model: Teradata Warehouse Miner User Guide - Volume 3 111 Chapter 1: Analytic Algorithms Linear Regression Figure 60: Linear Regression Tutorial: Linear Weights Graph Select the Graphics Options tab and change the Graph Type to Standardized Coefficient to view the standardized coefficient values. Although not generated automatically, a Scatter Plot is useful for analyzing the model built with the Linear Regression analysis. As an example, a scatter plot is brought up to look at the dependent variable (“cc_rev”), with the first two independent variables that made it into the model (“avg_cc_bal,” “income”). Create a new Scatter Plot analysis, and pick these three variables in the Selected Tables and Columns option. The results are shown first in two dimensions (avg_cc_bal and cc_rev), and then with all three: 112 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Linear Regression Figure 61: Linear Regression Tutorial: Scatter Plot (2d) Figure 62: Linear Regression Tutorial: Scatter Plot (3d) Teradata Warehouse Miner User Guide - Volume 3 113 Chapter 1: Analytic Algorithms Logistic Regression Logistic Regression Overview In many types of regression problems, the response variable or dependent variable to be predicted has only two possible outcomes. For example, will the customer buy the product in response to the promotion or not? Is the transaction fraudulent or not? Will the customer close their account or not? There are many examples of business problems with only two possible outcomes. Unfortunately the linear regression model comes up short in finding solutions to this type of problem. It is worth trying to understand what these shortcomings are and how the logistic regression model is an improvement when predicting a two-valued response variable. When the response variable y has only two possible values, which may be coded as a 0 and 1, the expected value of yi, E(yi), is actually the probability that the value will be 1. The error term for a linear regression model for a two-valued response function also has only two possible values, so it doesn't have a normal distribution or constant variance over the values of the independent variables. Finally, the regression model can produce a value that doesn't fall within the necessary constraint of 0 to 1. What would be better would be to compute a continuous probability function between 0 and 1. In order to achieve this continuous probability function, the usual linear regression expression b0 + b1x1 + ... + bnxn is transformed using a function called a logit transformation function. This function is an example of a sigmoid function, so named because it looks like a sigma or 's' when plotted. It is of course the logit transformation function that gives rise to the term logistic regression. The type of logistic regression model that Teradata Warehouse Miner supports is one with a two-valued dependent variable, referred to as a binary logit model. However, Teradata Warehouse Miner is capable of coding values for the dependent variable so that the user is not required to code their dependent variable to two distinct values. The user can choose which values to represent as the response value (i.e. 1 or TRUE) and all other will be treated as nonresponse values (i.e. 0 or FALSE). Even though values other than 1 and 0 are supported in the dependent variable, throughout this section the dependent variable response value is represented as 1 and the non-response value as 0 for ease of reading. The primary sources of information and formulae in this section are [Hosmer] and [Neter]. Logit model The logit transformation function is chosen because of its mathematical power and simplicity, and because it lends an intuitive understanding to the coefficients eventually created in the model. The following equations describe the logistic regression model, with x being the probability that the dependent variable is 1, and g(x) being the logit transformation: b +b x ++b x n n e 0 1 x x = -------------------------------------------------b + b x + + bn xn 1+e 0 1 x 114 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression x g x = ln -------------------- = b 0 + b 1 x 1 + b n x n 1 – x Notice that the logit transformation g(x) has linear parameters (b-values) and may be continuous with unrestricted range. Using these functions, a binomial error distribution is found with y = x + . The solution to a logistic regression model is to find the b-values that “best” predict the dichotomous y variable based on the values of the numeric x variables. Maximum likelihood In linear regression analysis it is possible to use a least-squares approach to finding the best bvalues in the linear regression equation. The least-squared error approach leads to a set of n normal equations in n unknowns that can be solved for directly. But that approach does not work here for logistic regression. Suppose any b-values are selected and the question is asked what is the likelihood that they match the logistic distribution defined, using statistical principles and the assumption that errors have a normal probability distribution. This technique of picking the most likely b-values that match the observed data is known as a maximum likelihood solution. In the case of linear regression, a maximum likelihood solution turns out to be mathematically equivalent to a least squares solution. But here maximum likelihood must be used directly. For convenience, compute the natural logarithm of the likelihood function so that it is possible to convert the product of likelihood’s into a sum, which is easier to work with. The log likelihood equation for a given vector B of b-values with v x-variables is given by: n n yi B'X – ln 1 + exp B'X ln L b 0 b v = i=1 i=1 where B’X = b0 + b1x1 + ... + bvxv. By differentiating this equation with respect to the constant term b0 and with respect to the variable terms bi, the likelihood equations are derived: n yi – xi = 0 i=1 and n xi yi – xi = 0 i=1 where Teradata Warehouse Miner User Guide - Volume 3 115 Chapter 1: Analytic Algorithms Logistic Regression exp B'X x i = --------------------------------1 + exp B'X The log likelihood equation is not linear in the unknown b-value parameters, so it must be solved using non-linear optimization techniques described below. Computational technique Unlike with linear regression, logistic regression calculations cannot be based on an SSCP matrix. Teradata Warehouse Miner therefore dynamically generates SQL to perform the calculations required to solve the model, produce model diagnostics, produce success tables, and to score new data with a model once it is built. However, to enhance performance with small data sets, Teradata Warehouse Miner provides an optional in-memory calculation feature (that is also helpful when one of the stepwise options is used). This feature selects the data into the client system’s memory if it will fit into a user-specified maximum memory amount. The maximum amount of memory in megabytes to use is specified on the expert options tab of the analysis input screen. The user can adjust this value according to their workstation and network requirements. Setting this amount to zero will disable the feature. Teradata Warehouse Miner offers two optimization techniques for logistic regression, the default method of iteratively reweighted least squares (RLS), equivalent to the Gauss-Newton technique, and the quasi-Newton method of Broyden-Fletcher-Goldfarb-Shanno (BFGS). The RLS method is considerably faster than the BFGS method unless there are a large number of columns (RLS grows in complexity roughly as the square of the number of columns). Having a choice between techniques can be useful for more than performance reasons however, since there may be cases where one or the other technique has better convergence properties. You may specify your choice of technique, or allow Teradata Warehouse Miner to automatically select it for you. With the automatic option the program will select RLS if there are less than 35 independent variable columns; otherwise it will select BFGS. Logistic Regression Model Diagnostics Logistic regression has counterparts to many of the same model diagnostics available with linear regression. In a similar manner to linear regression, these diagnostics provide a mathematically sound way to evaluate a model built with logistic regression. Standard errors and statistics As is the case with linear regression, measurements are made of the standard error associated with each b-coefficient value. Similarly, the T-statistic or Wald statistic as it is also called, is calculated for each b-coefficient as the ratio of the b-coefficient value to its standard error. Along with its associated t-distribution probability value, it can be used to assess the statistical significance of this term in the model. The computation of the standard errors of the coefficients is based on a matrix called the information matrix or Hessian matrix. This matrix is the matrix of second order partial derivatives of the log likelihood function with respect to all possible pairs of the coefficient values. The formula for the “j, k” element of the information matrix is: 116 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression 2 n LB ------------------ = – x ik x ik i 1 – i B j B k i–1 where exp B'X x i = --------------------------------1 + exp B'X Unlike the case with linear regression, confidence intervals are not computed directly on the standard error values, but on something called the odds ratios, described below. Odds ratios and confidence intervals In linear regression, the meaning of each b-coefficient in the model can be thought of as the amount the dependent y variable changes when the corresponding independent x variable changes by 1. Because of the logit transformation, however, the meaning of each b-coefficient in a logistic regression model is not so clear. In a logistic regression model, the increase of an x variable by 1 implies a change in the odds that the outcome y variable will be 1 rather than 0. Looking back at the formula for the logit response function: x g x = ln -------------------- = b 0 + + b n x n 1 – x it is evident that the response function is actually the log of the odds that the response is 1, where x is the probability that the response is 1 and 1 – x is the probability that the response is 0. Now suppose that one of the x variables, say xj, varies by 1. Then the response function will vary by bj. This can be written as g(x0...xj + 1...xn) - g(x0...xj...xn) = bj. But it could also be written as: ln odds j + 1 ln odds j + 1 – ln odds j = ------------------------------- = b j odds j Therefore odds j + 1 -------------------- = exp b j odds j the formula for the odds ratio of the coefficient bj . By taking the exponent of a b-coefficient, one gets the odds ratio that is the factor by which the odds change due to a unit increase in xj. Because this odds ratio is the value that has more meaning, confidence intervals are calculated on odds ratios for each of the coefficients rather than on the coefficients themselves. The confidence interval is computed based on a 95% confidence level and a twotailed normal distribution. Teradata Warehouse Miner User Guide - Volume 3 117 Chapter 1: Analytic Algorithms Logistic Regression Logistic Regression Goodness of fit In linear regression one of the key measures associated with goodness of fit is the residual sums of squares RSS. An analogous measure for logistic regression is a statistic sometimes called the deviance. Its value is based on the ratio of the likelihood of a given model to the likelihood of a perfectly fitted or saturated model and is given by D = -2ln(ModelLH / SatModelLH). This can be rewritten D=-2LM + 2LS in terms of the model log likelihood and the saturated model log likelihood. Looking at the data as a set of n independent Bernoulli observations, LS is actually 0, so that D = -2LM. Two models can be contrasted by taking the difference between their deviance values, which leads to a statistic G = D1 - D2 = -2(L1 - L2). This is similar to the numerator in the partial F test in linear regression, the extra sums of squares or ESS mentioned in the section on linear regression. In order to get an assessment of the utility of the independent model terms taken as a whole, the deviance difference statistic is calculated for the model with a constant term only versus the model with all variables fitted. This statistic is then G = -2(L0 - LM). LM is calculated using the log likelihood formula given earlier. L0, the log likelihood of the constant only model with n observations is given by: L 0 = y ln y + n – y ln n – y – n ln n G follows a chi-square distribution with “variables minus one” degrees of freedom, and as such provides a probability value to test whether all the x-term coefficients should in fact be zero. Finally, there are a number of pseudo R-squared values that have been suggested in the literature. These are not truly speaking goodness of fit measures, but can nevertheless be useful in assessing the model. Teradata Warehouse Miner provides one such measure suggested by McFadden as (L0 - LM) / L0. [Agresti] Logistic Regression Data Quality Reports The same data quality reports optionally available for linear regression are also available when performing logistic regression. Since an SSCP matrix is not used in the logistic regression algorithm, additional internal processing is needed to produce data quality reports, especially for the Near Dependency report and the Detailed Collinearity Diagnostics report. Stepwise Logistic Regression Automated stepwise regression procedures are available for logistic regression to aid in model selection just as they are for linear regression. The procedures are in fact very similar to those described for linear regression. As such an attempt will be made to highlight the similarities and differences in the descriptions below. As is the case with stepwise linear regression, the automated stepwise procedures described below can provide insight into the variables that should be included in a logistic regression model. An element of human decision-making however is recommended in order to produce a model with useful business application. 118 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression Forward-Only Stepwise Logistic Regression The forward only procedure consists solely of forward steps as described below, starting without any independent x variables in the model. Forward steps are continued until no variables can be added to the model. Forward Stepwise Logistic Regression The forward stepwise procedure is a combination of the forward and backward steps always done in pairs, as described below, starting without any independent x variables in the model. One forward step is always followed by one backward step, and these single forward and backward steps are alternated until no variables can be added or removed. Additional checks are made after each step to see if the same variables exist in the model as existed after a previous step in the same direction. When this condition is detected in both the forward and backward directions the algorithm will also terminate. Backward-Only Stepwise Logistic Regression The backward only procedure consists solely of backward steps as described below, starting with all of the independent x variables in the model. Backward steps are continued until no variables can be removed from the model. Backward Stepwise Logistic Regression The backward stepwise procedure is a combination of the backward and forward steps always done in pairs, as described below, starting with all of the independent x variables in the model. One backward step is followed by one forward step, and these single backward and forward steps are alternated until no variables can be added or removed. Additional checks are made after each step to see if the same variables exist in the model as existed after a previous step in the same direction. When this condition is detected in both the backward and forward directions the algorithm will also terminate. Stepwise Logistic Regression - Forward step In stepwise linear regression the partial F statistic, or the analogous T-statistic probability value, is computed separately for each variable outside the model, adding each of them into the model one at a time. The analogous procedure for logistic regression would consist of computing the likelihood ratio statistic G, described in the Goodness of Fit section, for each variable outside the model, selecting the variable that results in the largest G value when added to the model. In the case of logistic regression however this becomes an expensive proposition because the solution of the model for each variable requires another iterative maximum likelihood solution, contrasted to the more rapidly achieved closed form solution available in linear regression. What is needed is a statistic that can be calculated without requiring an additional maximum likelihood solution. Teradata Warehouse Miner uses such a statistic proposed by Peduzzi, Hardy and Holford that they call a W statistic. This statistic is comparatively inexpensive to compute for each variable outside the model and is therefore expedient to use as a criterion for selecting a variable to add to the model. The W statistic is assumed to follow a chi square distribution with one degree of freedom due to its similarity to other statistics, and it gives evidence of behaving similarly to the likelihood ratio statistic. Therefore, the variable with the smallest chi square probability or P-value associated with its W statistic is added to the Teradata Warehouse Miner User Guide - Volume 3 119 Chapter 1: Analytic Algorithms Logistic Regression model in a forward step if the P-value is less than the criterion to enter. If more than one variable has a P-value of 0, then the variable with the largest W statistic is entered. For more information, refer to [Peduzzi, Hardy and Holford]. Stepwise Logistic Regression - Backward step Each backward step seeks to remove those variables that have statistical significance below a certain level. This is done by first fitting the model with the currently selected variables, including the calculation of the probability or P-value associated with the T-statistic for each variable, which is the ratio of the b-coefficient to its standard error. The variable with the largest P-value is removed if it is greater than the criterion to remove. Logistic Regression and Missing Data Null values for columns in a logistic regression analysis can adversely affect results, so Teradata Warehouse Miner ensures that listwise deletion is effectively performed with logistic regression. This ensures that any row for which one of the independent or dependent variable columns is null will be left out of computations completely. Additionally, the Recode transformation function can be used to build a new column, substituting a fixed known value for null. Initiate a Logistic Regression Function Use the following procedure to initiate a new Logistic Regression analysis in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 63: Add New Analysis from toolbar 2 120 In the resulting Add New Analysis dialog box, click on Analytics under Categories and then under Analyses double-click on Logistic Regression: Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression Figure 64: Add New Analysis dialog 3 This will bring up the Logistic Regression dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Logistic Regression - INPUT - Data Selection On the Logistic Regression dialog click on INPUT and then click on data selection: Figure 65: Logistic Regression > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). Teradata Warehouse Miner User Guide - Volume 3 121 Chapter 1: Analytic Algorithms Logistic Regression 2 Select Columns From a Single Table • Available Databases (or Analyses) — All the databases (or analyses) that are available for the Logistic Regression analysis. • Available Tables — All the tables that are available for the Logistic Regression analysis. • Available Columns — Within the selected table or matrix, all columns which are available for the Logistic Regression analysis. • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can either insert columns as Dependent or Independent columns. Make sure you have the correct portion of the window highlighted. The Dependent variable column is the column whose value is being predicted by the logistic regression model. The algorithm requires that the Independent columns must be of numeric type (or contain numbers in character format). The Dependent column may be of any type. Logistic Regression - INPUT - Analysis Parameters On the Logistic Regression dialog click on INPUT and then click on analysis parameters: Figure 66: Logistic Regression > Input > Analysis Parameters On this screen select: • Regression Options • Convergence Criterion — The algorithm continues to repeatedly estimate the model coefficient values until either the difference in the log likelihood function from one iteration to the next is less than or equal to the convergence criterion or the maximum iterations is reached. Default value is 0.001. • Maximum iterations — The algorithm stops iterating if the maximum iterations is reached. The default value is 100. • Response Value — The value of the dependent variable that will represent the response value. All other dependent variable values will be considered a non-response value. • Include Constant Term (checkbox) — This option specifies that the logistic regression model should include a constant term. With a constant, the logistic equation can be thought of as: 122 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression b +b x ++b x n n e 0 1 x x = -------------------------------------------------b + b x + + bn xn 1+e 0 1 x x g x = ln -------------------- = b 0 + b 1 x 1 + b n x n 1 – x Without a constant, the equation changes to: b x ++b x n n e 1 x x = ----------------------------------------b x + + bn xn 1+e 1 x x g x = ln -------------------- = b 1 x 1 + b n x n 1 – x The default value is to include the constant term. • Stepwise Options — If selected, the algorithm is performed repeatedly with various combinations of independent variable columns to attempt to arrive at a final “best” model. The default is to not use Stepwise Regression. • Step Direction — (Selecting “None” turns off the Stepwise option). • Forward — Option for independent variables being added one at a time to an empty model, possibly removing a variable after a variable is added. • Forward Only — Option for qualifying independent variables being added one at a time. • Backward — Option for removing variables from an initial model containing all of the independent variables, possibly adding a variable after a variable is removed. • Backward Only — Option for independent variables being removed one at a time. • Criterion to Enter — An independent variable is only added to the model if its W statistic chi-square P-value is less than the specified criterion to enter. The default value is 0.05. • Criterion to Remove — An independent variable is only removed if its T-statistic Pvalue is greater than the specified criterion to remove. The default value is 0.05 for each. • Report Options • Prediction Success Table — Creates a prediction success table using sums of probabilities rather than estimates based on a threshold value. The default is to generate the prediction success table. • Multi-Threshold Success Table — This table provides values similar to those in the prediction success table, but based on a range of threshold values, thus allowing the user to compare success scenarios using different threshold values. The default is to generate the multi-threshold Success table. • Threshold Begin • Threshold End • Threshold Increment — Specifies the threshold values to be used in the multi- Teradata Warehouse Miner User Guide - Volume 3 123 Chapter 1: Analytic Algorithms Logistic Regression threshold success table. If the computed probability is greater than or equal to a threshold value, that observation is assigned a 1 rather than a 0. Default values are 0, 1 and .05 respectively. • Cumulative Lift Table — Produce a cumulative lift table for deciles based on probability values. The default is to generate the Cumulative Lift table. • (Data Quality Reports) — These are the same data quality reports provided for Linear Regression and Factor Analysis. However, in the case of Logistic Regression, the “Sums of squares and Cross Products” or SSCP matrix is not readily available since it is not input to the algorithm, so it is derived dynamically by the algorithm. If there are a large number of independent variables in the model it may be more efficient to use the Build Matrix function to build and save the matrix and the Linear Regression function to produce the Data Quality Reports listed below. • Variable Statistics — This report gives the mean value and standard deviation of each variable in the model based on the derived SSCP matrix. • Near Dependency — This report lists collinear variables or near dependencies in the data based on the derived SSCP matrix. • • Condition Index Threshold — Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The one that involves this parameter is the occurrence of a large condition index value associated with a specially constructed principal factor. If a factor has a condition index greater than this parameter’s value, it is a candidate for the Near Dependency report. A default value of 30 is used as a rule of thumb. • Variance Proportion Threshold — Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The one that involves this parameter is when two or more variables have a variance proportion greater than this threshold value for a factor with a high condition index. Another way of saying this is that a ‘suspect’ factor accounts for a high proportion of the variance of two or more variables. This parameter defines what a high proportion of variance is. A default value of 0.5 is used as a rule of thumb. Detailed Collinearity Diagnostics — This report provides the details behind the Near Dependency report, consisting of the “Eigenvalues of Unit Scaled X’X”, “Condition Indices” and “Variance Proportions” tables. Logistic Regression - INPUT - Expert Options On the Logistic Regression dialog click on INPUT and then click on expert options: Figure 67: Logistic Regression > Input > Expert Options On this screen select: 124 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression • Optimization Method • Automatic — The program selects Reweighted Least Squares (RLS) unless there are 35 or more independent variable columns, in which case Quasi-Newton BFGS is selected instead. This is the default option. • Quasi-Newton (BFGS) — The user may explicitly request this optimization technique attributed to Broyden-Fletcher-Goldfarb-Shanno. Quasi-Newton methods do not require a Hessian matrix of second partial derivatives of the objective function to be calculated explicitly, saving time in some situations. • Reweighted Least Squares (RLS) — The user may explicitly request this optimization technique equivalent to the Gauss-Newton method. It involves computing a matrix very similar to a Hessian matrix but is typically the fastest technique for logistic regression. • Performance • Maximum amount of data for in-memory processing — Enter a number of megabytes. • Use multiple threads when applicable — This flag indicates that multiple SQL statements may be executed simultaneously, up to 5 simultaneous executions as needed. It only applies when not processing in memory, and only to certain processing performed in SQL. Where and when multi-threading is used is dependent on the number of columns and the Optimization Method selected (but both RLS and BFGS can potentially make some use of multi-threading). Logistic Regression - OUTPUT On the Logistic Regression dialog click on OUTPUT: Figure 68: Logistic Regression > OUTPUT On this screen select: • Store the variables table of this analysis in the database — Check this box to store the model variables table of this analysis in in the database. • Database Name — The name of the database to create the output table in. • Output Table Name — The name of the output table. • Advertise Output — The Advertise Output option "advertises" output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases Teradata Warehouse Miner User Guide - Volume 3 125 Chapter 1: Analytic Algorithms Logistic Regression tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. By way of an example, the tutorial example produces the following output table: Table 40: Logistic Regression - OUTPUT Standardi zed Coefficie nt Column Name B Coefficie nt years_ with_ bank 0.044251 4.914916 0.026929 0.906555 0.831242 0.988692 0.098102 11 2.216961 39 5 6 0.053055 0.144717 98 14 1 avg_sv_ tran_cnt 0.213310 31.22951 3.22526 1.192052 7 5.588337 E-08 avg_sv_ tran_amt 0.030762 0.003824 64.70387 8.043871 3.552714 1.03124 34 32 E-15 ckacct 0.465670 0.236528 3.876044 1.968767 0.049353 1.593081 1.002084 2.53263 2 8 13 avg_ck_ tran_cnt 0.009613 5.608763 0.018127 0.977489 0.959244 0.996082 0.022767 534 2.368283 26 7 1 3 0.059032 0.179196 57 84 4 married 0.233367 7.115234 -2.66744 0.622493 6 9 Standard Error Wald Statistic T Statistic P-Value Odds Ratio Lower Upper Partial R 0.303597 0.199861 0.461178 6 2 0.168006 0.914416 5 2 1.02354 1.038999 0.246071 2.061767 7 0.042563 0.127321 37 6 0.007810 0.536604 0.339634 0.847807 519 5 2 3 0.070282 0.171455 51 6 (Constan 0.273292 18.84624 1.614427 t) 1.186426 9 4.341225 E-05 avg_sv_ bal 0.003125 0.000559 31.16868 5.582892 3.323695 1.00313 305 8004 E-08 1.00203 1.004231 0.167831 2.625869 3 If Database Name is twm_results and Output Table Name is test, the output table is defined as: CREATE SET TABLE twm_results.test ( "Column Name" VARCHAR(30) CHARACTER SET UNICODE NOT CASESPECIFIC, "B Coefficient" FLOAT, "Standard Error" FLOAT, "Wald Statistic" FLOAT, "T Statistic" FLOAT, "P-Value" FLOAT, "Odds Ratio" FLOAT, "Lower" FLOAT, "Upper" FLOAT, "Partial R" FLOAT, "Standardized Coefficient" FLOAT) UNIQUE PRIMARY INDEX ( "Column Name" ); 126 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression Run the Logistic Regression After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Logistic Regression The results of running the Teradata Warehouse Miner Linear Regression analysis include a variety of statistical reports on the individual variables and generated model as well as barcharts displaying coefficients and T-statistics. All of these results are outlined below. The title of this report is preceded by the name of the technique that was used to build the model either Reweighted Least Squares Logistic Regression or Quasi-Newton (BFGS) Logistic Regression. On the Logistic Regression dialog, click on RESULTS (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed) to view results. Result options are as follows: • Data Quality Reports • Variable Statistics — If selected on the Results Options tab, this report gives the mean value and standard deviation of each variable in the model based on the SSCP matrix provided as input. • Near Dependency — If selected on the Results Options tab, this report lists collinear variables or near dependencies in the data based on the SSCP matrix provided as input. Entries in the Near Dependency report are triggered by two conditions occurring simultaneously. The first is the occurrence of a large condition index value associated with a specially constructed principal factor. If a factor has a condition index greater than the parameter specified on the Results Option tab, it is a candidate for the Near Dependency report. The other is when two or more variables have a variance proportion greater than a threshold value for a factor with a high condition index. Another way of saying this is that a ‘suspect’ factor accounts for a high proportion of the variance of two or more variables. The parameter to defines what a high proportion of variance is also set on the Results Option tab. A default value of 0.5. • Detailed Collinearity Diagnostics — If selected on the Results Options tab, this report provides the details behind the Near Dependency report, consisting of the following tables. • Eigenvalues of Unit Scaled X'X — Report of the eigenvalues of all variables scaled so that each variable adds up to 1 when summed over all the observations or rows. In order to calculate the singular values of X (the rows of X are the observations), the mathematically equivalent square root of the eigenvalues of XTX are computed instead for practical reasons • Condition Indices — The condition index of each eigenvalue, calculated as the Teradata Warehouse Miner User Guide - Volume 3 127 Chapter 1: Analytic Algorithms Logistic Regression square root of the ratio of the largest eigenvalue to the given eigenvalue, a value always 1 or greater. • Variance Proportions — The variance decomposition of these eigenvalues is computed using the eigenvalues together with the eigenvectors associated with them. The result is a matrix giving, for each variable, the proportion of variance associated with each eigenvalue. • Logistic Regression Step N (Stepwise-only) • In Report — This report is the same as the Variables in Model report, but it is provided for each step during stepwise logistic regression based on the variables currently in the model at each step. • Out Report • Column Name — The independent variable excluded from the model. • W Statistic — The W Statistic is a specialized statistic designed to determine the best variable to add to a model without calculating a maximum likelihood solution for each variable outside the model. The W statistic is assumed to follow a chi square distribution with one degree of freedom due to its similarity to other statistics, and it gives evidence of behaving similarly to the likelihood ratio statistic. For more information, refer to [Peduzzi, Hardy and Holford]. • Chi Sqr P-value — The W statistic is assumed to follow a chi square distribution on one degree of freedom due to its similarity to other statistics, and it gives evidence of behaving similarly to the likelihood ratio statistic. Therefore, the variable with the smallest chi square probability or P-value associated with its W statistic is added to the model in a forward step if the P-value is less than the criterion to enter. • Logistic Regression Model • Total Observations — This is the number of rows in the table that the logistic regression analysis is based on. The number of observations reflects the row count after any rows were eliminated by listwise deletion (due to one of the variables being null). • Total Iterations — The number of iterations used by the non-linear optimization algorithm in maximizing the log likelihood function. • Initial Log Likelihood — The initial log likelihood is the log likelihood of the constant only model and is given only when the constant is included in the model. The formula for initial log likelihood is given by: L 0 = y ln y + n – y ln n – y – n ln n where n is the number of observations. 128 • Final Log Likelihood — This is the value of the log likelihood function after the last iteration. • Likelihood Ratio Test G Statistic — Deviance, given by D = -2LM, where LM is the log likelihood of the logistic regression model, is a measure analogous to the residual sums of squares RSS in a linear regression model. In order to assess the utility of the independent terms taken as a whole in the logistic regression model, the deviance Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression difference statistic G is calculated for the model with a constant term only versus the model with all variables fitted. This statistic is then G = -2(L0 - LM), where L0 is the log likelihood of a model containing only a constant. The G statistic, like the deviance D, is an example of a likelihood ratio test statistic. • Chi-Square Degrees of Freedom — The G Statistic follows a chi-square distribution with “variables minus one” degrees of freedom. This field then is the degrees of freedom for the G Statistic’s chi-square test. • Chi-Square Value — This is the chi-square random variable value for the Likelihood Ratio Test G Statistic. This can be used to test whether all the independent variable coefficients should be 0. Examining the field Chi-square Probability is however the easiest way to assess this test. • Chi-Square Probability — This is the chi-square probability value for the Likelihood Ratio Test G Statistic. It can be used to test whether all the independent variable coefficients should be 0. That is, the probability that a chi-square distributed variable would have the value G or greater is the probability associated with having all 0 coefficients. The null hypothesis that all the terms should be 0 can be rejected if this probability is sufficiently small, say less than 0.05. • McFadden's Pseudo R-Squared — To mimic the Squared Multiple Correlation Coefficient (R2) in a linear regression model, the researcher McFadden suggested this measure given by (L0 - LM) / L0 where L0 is the log likelihood of a model containing only a constant and LM is the log likelihood of the logistic regression model. Although it is not truly speaking a goodness of fit measure, it can be useful in assessing a logistic regression model. (Experience shows that the value of this statistic tends to be less than the R2 value it mimics. In fact, values between 0.20 and 0.40 are quite satisfactory). • Dependent Variable Name — Column chosen as the dependent variable. • Dependent Variable Response Values — The response value chosen for the dependent variable on the Regression Options tab. • Dependent Variable Distinct Values — The number of distinct values that the dependent variable takes on. • Logistic Regression Variables in Model report • Column Name — This is the name of the independent variable in the model or CONSTANT for the constant term. • B Coefficient — The b-coefficient is the coefficient in the logistic regression model for this variable. The following equations describe the logistic regression model, with being the probability that the dependent variable is 1, and g(x) being the logit transformation: b +b x ++b x n n e 0 1 x x = -------------------------------------------------b + b x + + bn xn 1+e 0 1 x x g x = ln -------------------- = b 0 + b 1 x 1 + b n x n 1 – x Teradata Warehouse Miner User Guide - Volume 3 129 Chapter 1: Analytic Algorithms Logistic Regression • Standard Error — The standard error of a b-coefficient in the logistic regression model is a measure of its expected accuracy. It is analogous to the standard error of a coefficient in a linear regression model. • Wald Statistic — The Wald statistic is calculated as the square of the T-statistic (T Stat) described below. The T-statistic is calculated for each b-coefficient as the ratio of the b-coefficient value to its standard error. • T Statistic — In a manner analogous to linear regression, the T-statistic is calculated for each b-coefficient as the ratio of the b-coefficient value to its standard error. Along with its associated t-distribution probability value, it can be used to assess the statistical significance of this term in the model. • P-value — This is the t-distribution probability value associated with the T-statistic (T Stat), that is, the ratio of the b-coefficient value (B Coef) to its standard error (Std Error). It can be used to assess the statistical significance of this term in the logistic regression model. A value close to 0 implies statistical significance and means this term in the model is important. (The P-value represents the probability that the null hypothesis is true, that is the observation of the estimated coefficient value is chance occurrence - i.e. the null hypothesis is that the coefficient equals zero. The smaller the P-value, the stronger the evidence for rejecting the null hypothesis that the coefficient is actually equal to zero. In other words, the smaller the P-value, the larger the evidence that the coefficient is different from zero). • Odds Ratio — The odds ratio for an independent variable in the model is calculated by taking the exponent of the b-coefficient. The odds ratio is the factor by which the odds of the dependent variable being 1 change due to a unit increase in this independent variable. • Lower — Because of the intuitive meaning of the odds ratio, confidence intervals for coefficients in the model are calculated on odds ratios rather than on the coefficients themselves. The confidence interval is computed based on a 95% confidence level and a two-tailed normal distribution. “Lower” is the lower range of this confidence interval. • Upper — Because of the intuitive meaning of the odds ratio, confidence intervals for coefficients in the model are calculated on odds ratios rather than on the coefficients themselves. The confidence interval is computed based on a 95% confidence level and a two-tailed normal distribution. “Upper” is the upper range of this confidence interval. • Partial R — The Partial R statistic is calculated for each b-coefficient value as: wi – 2 Sign b i -------------– 2L 0 where bi is the b-coefficient and wi is the Wald Statistic of the ith independent variable, while L0 is the initial log likelihood of the model. (Note that if wi <= 2 then Partial R is set to 0). This statistic provides a measure of the relative importance of each 130 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression variable in the model. It is calculated only when the constant term is included in the model. [SPSS] • Standardized Coefficient — The estimated standardized coefficient is calculated for each b-coefficient value as: b i i ------- 3 where bi is the b-coefficient, i is the standard deviation of the ith independent 3 variable, and ------- is the standard deviation of the standard logistic distribution. This calculation only provides an estimate of the standardized coefficients since it uses a constant value for the logistic distribution without regard to the actual distribution of the dependent variable in the model. [Menard] • Prediction Success Table — The prediction success table is computed using only probabilities and not estimates based on a threshold value. Using an input table that contains known values for the dependent variable, the sum of the probability values x and 1 – x , which correspond to the probability that the predicted value is 1 or 0 respectively, are calculated separately for rows with actual value of 1 and 0. Refer to the Model Evaluation section for more information. • Estimate Response — The entries in the “Estimate Response” column are the sums of the probabilities x that the outcome is 1, summed separately over the observations where the actual outcome is 1 and 0 and then totaled. (Note that this is independent of the threshold value that is used in scoring to determine which probabilities correspond to an estimate of 1 and 0 respectively). • Estimate Non-Response — The entries in the “Estimate Non-Response” column are the sums of the probabilities 1 – x that the outcome is 0, summed separately over the observations where the actual outcome is 1 and 0 and then totaled. (Note that this is independent of the threshold value that is used in scoring to determine which probabilities correspond to an estimate of 1 and 0 respectively). • Actual Total — The entries in this column are the sums of the entries in the Estimate Response and Estimate Non-Response columns, across the rows in the Prediction Success Table. But in fact this turns out to be the number of actual 0’s and 1’s and total observations in the training data. • Actual Response — The entries in the “Actual Response” row correspond to the observations in the data where the actual value of the dependent variable is 1. • Actual Non-Response — The entries in the “Actual Non-Response” row correspond to the observations in the data where the actual value of the dependent variable is 0. • Estimated Total — The entries in this row are the sums of the entries in the Actual Response and Actual Non-Response rows, down the columns in the Prediction Success Table. This turns out to be the sum of the probabilities of estimated 0’s and 1’s and total observations in the model. • Multi-Threshold Success Table — This table provides values similar to those in the prediction success table, but instead of summing probabilities, the estimated values based Teradata Warehouse Miner User Guide - Volume 3 131 Chapter 1: Analytic Algorithms Logistic Regression on a threshold value are summed instead. Rather than just one threshold however, several thresholds ranging from a user specified low to high value are displayed in user specified increments. This allows the user to compare several success scenarios using different threshold values, to aid in the choice of an ideal threshold. Refer to the Model Evaluation section for more information. • Threshold Probability — This column gives various incremental values of the probability at or above which an observation is to have an estimated value of 1 for the dependent variable. For example, at a threshold of 0.5, a response value of 1 is estimated if the probability predicted by the logistic regression model is greater than or equal to 0.5. The user may request the starting, ending and increment values for these thresholds. • Actual Response, Estimate Response — This column corresponds to the number of observations for which the model estimated a value of 1 for the dependent variable and the actual value of the dependent variable is 1. • Actual Response, Estimate Non-Response — This column corresponds to the number of observations for which the model estimated a value of 0 for the dependent variable but the actual value of the dependent variable is 1, a “false negative” error case for the model. • Actual Non-Response, Estimate Response — This column corresponds to the number of observations for which the model estimated a value of 1 for the dependent variable but the actual value of the dependent variable is 0, a “false positive” error case for the model. • Actual Non-Response, Estimate Non-Response — This column corresponds to the number of observations for which the model estimated a value of 0 for the dependent variable and the actual value of the dependent variable is 0. • Cumulative Lift Table — The Cumulative Lift Table demonstrates how effective the model is in estimating the dependent variable. It is produced using deciles based on the probability values. Note that the deciles are labeled such that 1 is the highest decile and 10 is the lowest, based on the probability values calculated by logistic regression. The information in this report however is best viewed in the Lift Chart produced as a graph under a logistic regression analysis. 132 • Decile — The deciles in the report are based on the probability values predicted by the model. Note that 1 is the highest decile and 10 is the lowest. That is, decile 1 contains data on the 10% of the observations with the highest estimated probabilities that the dependent variable is 1. • Count — This column contains the count of observations in the decile. • Response — This column contains the count of observations in the decile where the actual value of the dependent variable is 1. • Response (%) — This column contains the percentage of observations in the decile where the actual value of the dependent variable is 1. • Captured Response (%) — This column contains the percentage of responses in the decile over all the responses in any decile. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression • Lift — The lift value is the percentage response in the decile (Pct Response) divided by the expected response, where the expected response is the percentage of response or dependent 1-values over all observations. For example, if 10% of the observations overall have a dependent variable with value 1, and 20% of the observations in decile 1 have a dependent variable with value 1, then the lift value within decile 1 is 2.0, meaning that the model gives a “lift” that is better than chance alone by a factor of two in predicting response values of 1 within this decile. • Cumulative Response — This is a cumulative measure of Response, from decile 1 to this decile. • Cumulative Response (%) — This is a cumulative measure of Pct Response, from decile 1 to this decile. • Cumulative Captured Response (%) — This is a cumulative measure of Pct Captured Response, from decile 1 to this decile. • Cumulative Lift — This is a cumulative measure of Lift, from decile 1 to this decile. Logistic Regression Graphs The Logistic Regression Analysis can display bar chars for the T-statistics, Wald Statistics, Log Odds Ratios, Partial R and Estimated Standard Coefficients of the resultant model. In addition, a Lift Chart in deciles is generated. Logistic Weights Graph This graph displays the relative magnitudes of the T-statistics, Wald Statistics, Log Odds Ratios, Partial R and Estimated Standard Coefficients associated with each variable in the logistic regression model. The sign, positive or negative, is portrayed by the colors red or blue respectively. The user may scroll to the left or right to see all the variables associated statistics in the model. The following options are available on the Graphics Options tab on the Logistic Weights graph: • Graph Type — The following can be graphed by the Linear Weights Graph • Vertical Axis — The user may request multiple vertical axes in order to display separate coefficient values that are orders of magnitude different from the rest of the values. If the coefficients are of roughly the same magnitude, this option is grayed out. • Single — Display the selected statistics on single axis on the bar chart. • Multiple — Display the selected statistics on dual axes on the bar chart. Lift Chart This graph displays the statistics in the Cumulative Lift Table, with the following options: • Non-Cumulative • % Response — This column contains the percentage of observations in the decile where the actual value of the dependent variable is 1. • % Captured Response — This column contains the percentage of responses in the decile over all the responses in any decile. Teradata Warehouse Miner User Guide - Volume 3 133 Chapter 1: Analytic Algorithms Logistic Regression • Lift — The lift value is the percentage response in the decile (Pct Response) divided by the expected response, where the expected response is the percentage of response or dependent 1-values over all observations. For example, if 10% of the observations overall have a dependent variable with value 1, and 20% of the observations in decile 1 have a dependent variable with value 1, then the lift value within decile 1 is 2.0, meaning that the model gives a “lift” that is better than chance alone by a factor of two in predicting response values of 1 within this decile. • Cumulative • % Response — This is a cumulative measure of the percentage of observations in the decile where the actual value of the dependent variable is 1, from decile 1 to this decile. • % Captured Response — This is a cumulative measure of the percentage of responses in the decile over all the responses in any decile, from decile 1 to this decile. • Cumulative Lift — This is a cumulative measure of the percentage response in the decile (Pct Response) divided by the expected response, where the expected response is the percentage of response or dependent 1-values over all observations, from decile 1 to this decile. Tutorial - Logistic Regression The following is an example of using the stepwise feature of Logistic Regression analysis. The stepwise feature adds extra processing steps to the analysis; that is, normal Logistic Regression processing is a subset of the output shown below. In this example, ccacct (has credit card, 0 or 1) is being predicted in terms of 16 independent variables, from income to avg_sv_tran_cnt. The forward stepwise process determines that only 7 out of the original 16 input variables should be used in the model. These include avg_sv_tran_amt (average amount of savings transactions), avg_sv_tran_cnt (average number of savings transactions per month), avg_sv_bal (average savings account balance), married, years_with_bank, avg_ck_ tran_cnt (average number of checking transactions per month), and ckacct (has checking account, 0 or 1). Step 0 shows that all of the original 16 independent variables are excluded from the model, the starting point for forward stepwise regression. In Step 1, the Model Assessment report shows that the variable avg_sv_tran_amt added to the model, along with the constant term, with all other variables still excluded from the model. For the sake of brevity, Steps 2 through 6 are not shown. Then in Step 7, the variable ckacct is the last variable added to the model. At this point the stepwise algorithm stops because there are no more variables qualifying to be added or removed from the model, and the Reweighted Least Squares Logistic Regression and Variables in Model reports are given, just as they would be if these variables were analyzed without stepwise requested. Finally the Prediction Success Table, Multi-Threshold Success Table, and Cumulative Lift Table are given, as requested, to complete the analysis. Parameterize a Logistic Regression Analysis as follows: • Available Table — twm_customer_analysis • Dependent Variable — cc_acct 134 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression • Independent Variables • income — age • years_with_bank — nbr_children • female — single • married — separated • ckacct — svacct • avg_ck_bal — avg_sv_bal • avg_ck_tran_amt — avg_ck_tran_cnt • avg_sv_tran_amt — avg_sv_tran_cnt • Convergence Criterion — 0.001 • Maximum Iterations — 100 • Response Value — 1 • Include Constant — Enabled • Prediction Success Table — Enabled • Multi-Threshold Success Table — Enabled • Threshold Begin — 0 • Threshold End — 1 • Threshold Increment — 0.05 • Cumulative Lift Table — Enabled • Use Stepwise Regression — Enabled • Criterion to Enter — 0.05 • Criterion to Remove — 0.05 • Direction — Forward • Optimization Type — Automatic Run the analysis, and click on Results when it completes. For this example, the Logistic Regression Analysis generated the following pages. A single click on each page name populates Results with the item. Table 41: Logistic Regression Report Total Observations: 747 Total Iterations: 9 Initial Log Likelihood: -517.7749 Final Log Likelihood: -244.4929 Likelihood Ratio Test G Statistic: 546.5641 Chi-Square Degrees of Freedom: 7.0000 Chi-Square Value: 14.0671 Chi-Square Probability: 0.0000 Teradata Warehouse Miner User Guide - Volume 3 135 Chapter 1: Analytic Algorithms Logistic Regression Table 41: Logistic Regression Report McFadden's Pseudo R-Squared: 0.5278 Dependent Variable: ccacct Dependent Response Value: 1 Total Distinct Values: 2 Table 42: Execution Summary 136 6/20/2004 2:19:02 PM Stepwise Logistic Regression Running. 6/20/2004 2:19:03 PM Step 0 Complete 6/20/2004 2:19:03 PM Step 1 Complete 6/20/2004 2:19:03 PM Step 2 Complete 6/20/2004 2:19:03 PM Step 3 Complete 6/20/2004 2:19:03 PM Step 4 Complete 6/20/2004 2:19:04 PM Step 5 Complete 6/20/2004 2:19:04 PM Step 6 Complete 6/20/2004 2:19:04 PM Step 7 Complete 6/20/2004 2:19:04 PM Log Likelihood: -517.78094387828 6/20/2004 2:19:04 PM Log Likelihood: -354.38456690558 6/20/2004 2:19:04 PM Log Likelihood: -287.159936852895 6/20/2004 2:19:04 PM Log Likelihood: -258.834546711159 6/20/2004 2:19:04 PM Log Likelihood: -247.445356552554 6/20/2004 2:19:04 PM Log Likelihood: -244.727173470081 6/20/2004 2:19:04 PM Log Likelihood: -244.49467692232 6/20/2004 2:19:04 PM Log Likelihood: -244.492882024522 6/20/2004 2:19:04 PM Log Likelihood: -244.492881920691 6/20/2004 2:19:04 PM Computing Multi-Threshold Success Table 6/20/2004 2:19:06 PM Computing Prediction Success Table 6/20/2004 2:19:06 PM Computing Cumulative Lift Table 6/20/2004 2:19:07 PM Creating Report Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression Table 43: Variables Column Name B Standard Coefficient Error Wald Statistic T Statistic P-Value Odds Ratio Lower Upper Partial R Standardized Coefficient (Constant) -1.1864 0.2733 18.8462 -4.3412 0.0000 N/A N/A N/A N/A N/A avg_sv_ tran_amt 0.0308 0.0038 64.7039 8.0439 0.0000 1.0312 1.0235 1.0390 0.2461 2.0618 avg_sv_ tran_cnt -1.1921 0.2133 31.2295 -5.5883 0.0000 0.3036 0.1999 0.4612 -0.1680 -0.9144 avg_sv_bal 0.0031 0.0006 31.1687 5.5829 0.0000 1.0031 1.0020 1.0042 0.1678 2.6259 married -0.6225 0.2334 7.1152 -2.6674 0.0078 0.5366 0.3396 0.8478 -0.0703 -0.1715 years_with_ -0.0981 bank 0.0443 4.9149 -2.2170 0.0269 0.9066 0.8312 0.9887 -0.0531 -0.1447 avg_ck_ tran_cnt -0.0228 0.0096 5.6088 -2.3683 0.0181 0.9775 0.9592 0.9961 -0.0590 -0.1792 ckacct 0.4657 0.2365 3.8760 1.9688 0.0494 1.5931 1.0021 2.5326 0.0426 0.1273 Step 0 Table 44: Columns Out Column Name W Statistic Chi-Square P-Value age 1.9521 0.1624 avg_ck_bal 0.5569 0.4555 avg_ck_tran_amt 1.6023 0.2056 avg_ck_tran_cnt 0.0844 0.7714 avg_sv_bal 85.5070 0.0000 avg_sv_tran_amt 233.7979 0.0000 avg_sv_tran_cnt 44.0510 0.0000 ckacct 21.8407 0.0000 female 3.2131 0.0730 income 1.9877 0.1586 married 19.6058 0.0000 nbr_children 5.1128 0.0238 separated 5.5631 0.0183 single 6.9958 0.0082 svacct 7.4642 0.0063 Teradata Warehouse Miner User Guide - Volume 3 137 Chapter 1: Analytic Algorithms Logistic Regression Table 44: Columns Out Column Name W Statistic Chi-Square P-Value years_with_bank 3.0069 0.0829 Step 1 Table 45: Variables Column Name B Standard Coefficient Error Wald Statistic T Statistic P-Value Odds Ratio avg_sv_ tran_amt 0.0201 193.2455 13.9013 0.0000 1.0203 1.0174 1.0232 0.4297 0.0014 Lower Upper Partial R Standardized Coefficient 1.3445 Table 46: Columns Out 138 Column Name W Statistic Chi-Square P-Value age 3.4554 0.0630 avg_ck_bal 0.4025 0.5258 avg_ck_tran_amt 0.3811 0.5370 avg_ck_tran_cnt 11.3612 0.0007 avg_sv_bal 46.6770 0.0000 avg_sv_tran_cnt 134.8091 0.0000 ckacct 7.8238 0.0052 female 2.4111 0.1205 income 5.2143 0.0224 married 7.7743 0.0053 nbr_children 2.6647 0.1026 separated 3.9342 0.0473 single 2.7417 0.0978 svacct 2.0405 0.1532 years_with_bank 13.2617 0.0003 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Logistic Regression Step 2-7 Table 47: Prediction Success Table Estimate Response Estimate Non-Response Actual Total Actual Response 304.5868 70.4132 375.0000 Actual Non-Response 70.4133 301.5867 372.0000 Actual Total 375.0000 372.0000 747.0000 Table 48: Multi-Threshold Success Table Threshold Probability Actual Response, Estimate Response Actual Response, Estimate Non-Response Actual Non-Response, Estimate Response Actual Non-Response, Estimate Non-Response 0 375 0 372 0 .05 375 0 353 19 .1 374 1 251 121 .15 373 2 152 220 .2 369 6 90 282 .25 361 14 58 314 .3 351 24 37 335 .35 344 31 29 343 .4 329 46 29 343 .45 318 57 28 344 .5 313 62 24 348 .55 305 70 23 349 .6 291 84 23 349 .65 286 89 21 351 .7 276 99 20 352 .75 265 110 20 352 .8 253 122 20 352 .85 243 132 16 356 .9 229 146 13 359 .95 191 184 11 361 Teradata Warehouse Miner User Guide - Volume 3 139 Chapter 1: Analytic Algorithms Logistic Regression Table 49: Cumulative Lift Table Cumulative Response (%) Cumulative Captured Response (%) Cumulative Lift Decile Count Response Response (%) Captured Response (%) 1 74.0000 73.0000 98.6486 19.4667 1.9651 73.0000 98.6486 19.4667 1.9651 2 75.0000 69.0000 92.0000 18.4000 1.8326 142.0000 95.3020 37.8667 1.8984 3 75.0000 71.0000 94.6667 18.9333 1.8858 213.0000 95.0893 56.8000 1.8942 4 74.0000 65.0000 87.8378 17.3333 1.7497 278.0000 93.2886 74.1333 1.8583 5 75.0000 66.0000 88.0000 17.6000 1.7530 344.0000 92.2252 91.7333 1.8371 6 75.0000 24.0000 32.0000 6.4000 0.6374 368.0000 82.1429 98.1333 1.6363 7 74.0000 4.0000 5.4054 1.0667 0.1077 372.0000 71.2644 99.2000 1.4196 8 73.0000 2.0000 2.7397 0.5333 0.0546 374.0000 62.8571 99.7333 1.2521 9 69.0000 1.0000 1.4493 0.2667 0.0289 375.0000 56.4759 100.0000 1.1250 10 83.0000 0.0000 0.0000 0.0000 0.0000 375.0000 50.2008 100.0000 1.0000 Lift Cumulative Response Logistic Weights Graph By default, the Logistic Weights graph displays the relative magnitudes of the T-statistic associated with each coefficient in the logistic regression model: Figure 69: Logistic Regression Tutorial: Logistic Weights Graph 140 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Select the Graphics Options tab and change the Graph Type to Wald Statistic, Log Odds Ratio, Partial R or Estimated Standardized Coefficient to view those statistical measures respectively Lift Chart By default, the Lift Chart displays the cumulative measure of the percentage of observations in the decile where the actual value of the dependent variable is 1, from decile 1 to this decile (Cumulative, %Response): Figure 70: Logistic Regression Tutorial: Lift Chart Neural Networks Overview Note: The material in this overview was contributed by StatSoft®, Inc. Over the past two decades there has been an explosion of interest in neural networks. It started with the successful application of this powerful technique across a wide range of problem domains, in areas as diverse as finance, medicine, engineering, geology and even physics. The sweeping success of neural networks over almost every other statistical technique can be attributed to its power, versatility and ease of use. Neural networks are very sophisticated modeling and prediction-making techniques capable of modeling extremely complex functions and data relationships. The ability to learn by examples is one of the many features of neural networks which enables the user to model data and establish accurate rules governing the underlying relationship Teradata Warehouse Miner User Guide - Volume 3 141 Chapter 1: Analytic Algorithms Neural Networks between various data attributes. The neural network user gathers representative data, and then invokes training algorithms which can automatically learn the structure of the data. Although the user does need to have some heuristic knowledge of how to select and prepare data, the appropriate neural network, and interpret the results, the level of user knowledge needed to successfully apply neural networks is much lower than that needed in most traditional statistical tools and techniques. The neural network algorithms can be hidden behind a welldesigned and intelligent computer program which takes the user from start to finish with just a few clicks. Using neural networks Neural networks have a remarkable ability to derive and extract meaning, rules and trends from complicated, noisy and imprecise data. They can be used to extract patterns and detect trends that are governed by complicated mathematical functions too difficult, if not impossible, to model using analytic or parametric techniques. One of the abilities of neural networks is to accurately predict data that was not part of the training dataset, a process known as generalization. Given these characteristics with their broad applicability, neural networks are suitable for applications of real world problems in research and science, business and industry. Below are some examples where neural networks have been successfully applied: • Signal processing • Process control • Robotics • Classification • Data preprocessing • Pattern recognition • Image and speech analysis • Medical diagnostics and monitoring • Stock market and forecasting • Loan or credit solicitations The biological inspiration Neural networks are also intuitively appealing, since their principles are based on crude and low-level models of biological neural information processing systems. These have led to the development of more intelligent computer systems that can be used in statistical and data analysis tasks. Neural networks emerged out of research in artificial intelligence, inspired by attempts to mimic the fault-tolerance and “capacity to learn” of biological neural systems by modeling the low-level structure of the brain (see Patterson, 1996). The brain is principally composed of over ten billion neurons, massively interconnected with thousands of interconnects per neuron. Each neuron is a specialized cell that can create, propagate and receive electrochemical signals. Like any biological cell, neurons have a body, a branching input structure called dendrites and a branching output structure known as axons. The axons of one cell connect to the dendrites of another via a synapse. When a neuron is activated, it fires an electrochemical signal along the axon. This signal crosses the synapses to 142 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks thousands of other neurons, which in turn may fire, thus propagating the signal over the entire neural system (e.g. the biological brain). A neuron fires only if the total signal received at the cell body from the dendrites exceeds a certain level known as threshold. Though a single neuron accomplishes no meaningful task on its own, when the efforts of a large number of them are combined together, the results become quite dramatic: they can create or achieve various and extremely complex cognitive tasks such as learning and even consciousness. Thus, from a very large number of extremely simple processing units the brain manages to perform extremely complex tasks. Of course, there is a great deal of complexity in the brain that has not been discussed here, but it is interesting that artificial neural networks can achieve remarkable results using a model not much more complex than this. The basic mathematical model The following figure shows a Schematic of a single neuron system. The inputs x send signals to the neuron, at which a weighted sum of the signals is obtained and further transformed using a mathematical function f. Figure 71: Single Neuron System (schematic) Here we consider the simplest form of artificial neural networks, with a single neuron with a number of inputs and one (for simplicity) output. Although a more realistic artificial network typically consists of many more neurons, this model sheds light on the basics of this technology. The neuron receives signals from many sources. This source usually comes from the data referred to as input variables x or inputs for short. The inputs are received from a connection that has a certain strength, known as weights. The strength of a weight is represented by a number. The larger the value of a weight w, the stronger is its incoming signal and the more influential the corresponding input is. Upon receiving the signals, a weighted sum of the inputs is formed to compose the activation function f (“activation”) of the neuron. The neuron activation is a mathematical function which converts the weighted sum of the signals to form the output of the neuron. Thus: output = f(w1x1 + ... + wdxd) The outputs of the neuron are actually predictions of the single neuron model for a variable in the data which is referred to as the target t. It is believed that there is a relationship between the inputs x and the targets t; it is the task of the neural network to model this relationship by Teradata Warehouse Miner User Guide - Volume 3 143 Chapter 1: Analytic Algorithms Neural Networks relating the inputs to the targets via a suitable mathematical function which can be learned from examples in the data. Feedforward neural networks The artificially simple (“toy”) model discussed above is the simplest neural network model one can construct. This model is used to explain some of the basic functionality and principles of neural networks as well as to describe the individual neuron. As mentioned above, however, a single neuron cannot perform a meaningful task on its own. Instead many interconnected neurons are needed to achieve any specific goal. This takes us to considering more neural network architectures which are used in practical applications. The next question is “how should neurons be connected together?” If a network is to be of any use, there must be inputs (which carry the values of variables of interest in the outside world) and outputs (which form predictions, or control signals). Inputs and outputs correspond to sensory and motor nerves such as those coming from the eyes and leading to the hands. However, there also can be hidden neurons that play an internal role in the network. The input, hidden, and output neurons need to be connected together. The key issue here is feedback (Haykin, 1994). A simple network has a feedforward structure: signals flow from inputs, forwards through any hidden units, eventually reaching the output units. Such a structure has stable behavior and fault tolerance. Feedforward neural networks are by far the most useful in solving real problems and therefore are the most widely used. See Bishop 1995 for more information on various neural networks types and architectures. A typical feedforward network has neurons arranged in a distinct layered topology. Generally, the input layer simply serves to introduce the values of the input variables. The hidden and output layer neurons are each connected to all of the units in the preceding layer. Again, it is possible to define networks that are partially connected to only some units in the preceding layer. However, for most applications, fully connected networks are better, and this is the type of network supported by STATISTICA Automatic Neural Networks (SANN). When the network is executed, the input variable values are placed in the input units, and then the hidden and output layer units are progressively executed in sequential order. Each of them calculates its activation value by taking the weighted sum of the outputs of the units in the preceding layer. The activation value is passed through the activation function to produce the output of the neuron. When the entire network has been executed, the neurons of the output layer act as the output of the entire network. Neural network tasks Like most statistical models, neural networks are capable of performing three major tasks including regression, and classification. Regression tasks are concerned with relating a number of input variables x with set of continuous outcomes t (target variables). By contrast, classification tasks assign class memberships to a categorical target variable given a set of input values. In the next section we will consider regression in more details. Regression and the family of nonparametric (black-box) tools One of the most straightforward and perhaps simplest approach to statistical inference is to assume that the data can be modeled using a closed functional form which can contain a 144 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks number of adjustable parameters (weights) which can be estimated so the model can provide us with the best explanation of the data in hand. For example, consider a regression problem in which we are modeling or approximating a single target variable t as a linear function of an input variable x. The mathematical function used to model such relationship is simply given by a linear transformation f with two parameters, namely the intercept a and slope b: t = f(x) = a + bx Our task is to find suitable values for a and b which relates an input x to the variable t. This problem is known as the linear regression. Another example of parametric regression is the quadratic problem where the input output relationship is described by the quadratic form: t = f(x) = a + bx2 The following schematic shows the difference between parametric and nonparametric models. In parametric models the input-target relationship is described by a mathematical function of closed form. By contrast, in nonparametric models, the input-target relationship is governed by an approximator (like a neural network) which cannot be represented by a standard mathematical function. Figure 72: Parametric Model vs. Non-Parametric Model (schematic) The examples above belong to the category of the so-called parametric methods. They strictly rely on the assumption that t is related to x in a priori known way, or can be sufficiently approximated by a closed mathematical from, e.g. a line or a quadratic function. Once the mathematical function is chosen, all we have to do is to adjust the parameters of the assumed model so they best approximate (predict) t given an instance of x. By contrast, non-parametric models generally make no assumptions regarding the relationship of x and t. In other words they assume that the true underlying function governing the relationship between x and t is not known a priori, hence the term “black box”. Instead, they attempt to discover a mathematical function (which often does not have a closed form) that can approximate the representation of x & t sufficiently well. The most popular examples of non-parametric models are polynomial functions with adaptable parameters, and Teradata Warehouse Miner User Guide - Volume 3 145 Chapter 1: Analytic Algorithms Neural Networks indeed neural networks. Since no closed form for the relationship between x and t is assumed, the non-parametric method must be sufficiently flexible to be able to model a wide spectrum of functional relationships. The higher the order of a polynomial, for example, the more flexible the model is. Similarly, the more neurons a neural network has the stronger the model becomes. Parametric models enjoy the advantage of being easy to use and having outputs which are easy to interpret. On the other hand, they suffer from the disadvantage of limited flexibility. Consequently, their usefulness strictly depends on how well the assumed input-target relationship survives the test of reality. Unfortunately many of the real world problems do not simply lend themselves to a closed form and the parametric representation may often prove too restrictive. No wonder then that statisticians and engineers often consider using nonparametric models, especially neural networks, as alternatives to parametric methods. Neural networks and classification tasks Neural networks, like most statistical tools, can also be used to tackle classification problems. By contrast to regression problems, a neural network classifier assigns class membership to an input x. For example, if the input set has three categories {A, B, C}, a neural network assigns each and every input to one of the three classes. The class membership information is carried in the target variable t. For that reason, in a classification analysis the target variable must always be categorical. A variable is categorical if (a) it can only assume discrete values which (b) cannot be numerically arranged (ranked). For example, a target variable with {MALE, FEMALE} is two- state categorical variable. A target variable with date values, however, is not truly categorical since values can be ranked (arranged according in numerical order). The multilayer perceptron neural networks The following figure shows a schematic diagram of a fully connected MLP2 neural network with three inputs, four hidden units (neurons) and 3 outputs. Note that the hidden and output layers have a bias term. Bias is a neuron which emits signals with strength 1. 146 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 73: Fully connected MLP2 neural network with three inputs (schematic) Multilayer perceptrons MLP is perhaps the most popular network architecture in use today, credited originally to Rumelhart and McClelland (1986) and discussed at length in most neural network textbooks (Bishop, 1995). Each neuron performs a weighted sum of its inputs and passes it through a transfer function f to produce its output. For each neural layer in an MLP network there is also a bias term. A bias is a neuron with its activation function permanently set to 1. Just as in other neurons, a bias connects to the neurons in the layer above via a weight which is often called a threshold. The neurons and biases are arranged in a layered feedforward topology. The network thus has a simple interpretation as a form of input-output model, with the weights and thresholds as the free (adjustable) parameters of the model. Such networks can model functions of nearly arbitrary complexity, with the number of layers and the number of units in each layer determining the function complexity. Important issues in Multilayer Perceptrons design include specification of the number of hidden layers and the number of units in these layers (Bishop, 1995). Others include the choice of activation functions and methods of training. The following schematic shows the difference between MLP and RBF neural networks in two dimensional input data. One way to separate the clusters of inputs is to draw appropriate planes separating the various classes from one another. This method is used by MLP networks. An alternative approach is to fit each class of input data with a Gaussian basis function. Teradata Warehouse Miner User Guide - Volume 3 147 Chapter 1: Analytic Algorithms Neural Networks Figure 74: MLP vs. RBF neural networks in two dimensional input data (schematic) The radial basis function neural networks The following figure shows a schematic diagram of an RBF neural network with three inputs, four radial basis functions and 3 outputs. Note that in contrast to MLP networks, it is only the output units which have a bias term. Figure 75: RBF Neural Network with three inputs (schematic) Another type of neural network architecture used by SANN is known as Radial Basis Functions (RBF). RBF networks are perhaps the most popular type of neural networks after MLPs. In many ways, RBF is similar to MLP networks. First of all they too have unidirectional feedforward connections and every neuron is fully connected to the units in the layer above. The neurons are arranged in a layered feedforward topology. Nonetheless, RBF neural networks models are fundamentally different in the way they model the input-target relationship. While MLP networks model the input-target relationship in one stage, an RBF network partitions this learning process into two distinct and independent stages. In the first 148 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks stage and with the aid of the hidden layer neurons known as radial basis functions, the RBF network models the probability distribution of the input data. In the second stage, it learns how to relate an input data x to a target variable t. Note that unlike MLP networks, the bias term in an RBF neural network connects to the output neurons only. In other words, RBF networks do not have a bias term connecting the inputs to the radial basis units. In the rest of this document we will refer to both weights and thresholds as weights for short unless it is necessary to make a distinction. Like MLP, the activation function of the inputs is taken to be the identity. The signals from these inputs are passed to each radial basis unit in the hidden layer and the Euclidean distance between the input and a prototype vector is calculated for each neuron. This prototype vector is taken to be the location of the basis function in the space of the input data. Each neuron in the output layer performs a weighted sum of its inputs and passes it through a transfer function to produce its output. Therefore, unlike an MLP network, an RBF network has two types of parameters, (1) location and radial spread of the basis functions and (2) weights which connect these basis functions to the output units. Activation functions A mentioned above, a multilayer perceptron MLP is a feedforward neural network architecture with unidirectional full connections between successive layers. This does not, however, uniquely determine the property of a network. In addition to network architecture, the neurons of a network have activation functions which transform the incoming signals from the neurons of the previous layer using a mathematical function. The type of this function represents the activation function itself and can profoundly influence the network performance. Thus it is very important to choose a type of activation function for the neurons of a neural network. Input neurons usually have no activation function. In other words, they use the identity function, which means the input signals are not transformed at all. Instead they are combined in a weighted sum (weighted by the input-hidden layer weights) and passed on to the neurons in the layer above (usually called the hidden layer). For an MLP with two layers (MLP2) it is recommended that you use the tanh (hyperbolic) function, although other types are also possible such as the logistic sigmoid and exponential functions. The output neuron activation functions are in most cases set to identity, but this may vary from task to task. For example, in classification tasks it is set to softmax (Bishop 1995) while for regression problems they are set to identity (together with the choice of tanh for the hidden neurons). The set of neuron activation functions for the hidden and output neurons available in SANN is given in the table below: Table 50: Neuron Activation Functions for hidden/output neurons available in SANN Function Definition Identity Teradata Warehouse Miner User Guide - Volume 3 Description The activation of the neuron is passed on directly as the output. Range – 149 Chapter 1: Analytic Algorithms Neural Networks Table 50: Neuron Activation Functions for hidden/output neurons available in SANN Function Definition Logistic sigmoid 1 --------------–a 1–e Hyperbolic tangent e –e ----------------a –a e –e Exponential e Sine sin a Softmax Gaussian a –a –a exp a i ------------------------ exp ai 2 1 x – -------------- exp ----------------------2 2 2 Description Range An S-shaped curve. 0 1 A sigmoid curve similar to the logistic function. Often performs better than the logistic function because of its symmetry. Ideal for multilayer perceptrons, particularly the hidden layers. The negative exponential function. Possibly useful if recognizing radially distributed data. Not used by default. Mainly used for (but not restricted to) classification tasks. Useful for constructing neural networks with normalized multiple outputs which makes it particularly suitable for creating neural network classifiers with probabilistic outputs. – 1 1 0 0 1 0 1 This type of isotropic Gaussian activation function is solely used by the hidden units of an RBF neural network which are also known as radial basis functions. The location (also known as prototype vectors) and spread parameters are equivalent to the input-hidden layer weights of an MLP neural network. Selecting the input variables The number of input and output units is defined by the problem. The target (predicted dependent variable) is believed to depend on the inputs and so its choice is clear. Not so when it comes to selecting the inputs (independent variables). There may be some uncertainty about which inputs to use. Using a sufficient number of correct inputs is a matter of great 150 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks importance in predictive modeling (i.e. relating a target variable to a set of inputs) and indeed all forms of statistical analysis. By including irrelevant inputs, for example, one may inadvertently damage the performance of the neural network. On the other hand, a dataset with an insufficient number of inputs may never be accurately modeled by a neural network. Neural network complexity The complexity of a neural network (and the two layer perceptron MLP2 & Radial Basis Functions) is measured by the number of neurons in the hidden layer. The more neurons in a neural network, the greater the flexibility and complexity of the system. Flexible neural networks can be used to approximate any function complexity which relates the input-target variables. Thus in order to model a dataset, it is important to have a sufficiently flexible neural network with enough neurons in the hidden layer. The optimal number of neurons depends on the problem domain, but it is generally related to the number of inputs. Training of neural networks Once a neural network architecture is selected (i.e. neural network type), activation functions, etc., the remaining adjustable parameters of the model are the weights connecting the inputs to the hidden neurons and the hidden neurons to the output neurons. The process of adjusting these parameters so the network can approximate the underlying functional relationship between the inputs x and the targets t is known as “training”. It is in this process that the neural network learns to model the data by example. Although there are various methods to train neural networks, implementing most of them involve numeric algorithms which can complete the task in a finite number of iterations. The need for these iterative algorithms is primarily due to the highly nonlinear nature of neural network models for which a closed form solution is most often unavailable. An iterative training algorithm gradually adjusts the weights of the neural network so that for any given input data x the neural network can produce an output which is as close as possible to t. Weights initialization Because training neural networks require an iterative algorithm in which the weights are adjusted, the weights must first be initialized to reasonable starting values. This may sometimes affect not only the quality of the solution, but also the time needed to prepare the network (training). It is important that you initialize the weights using small weight values so at that at the start of training the network operates in a linear mode, and then let it increase the values of its weights to fit the data accurately enough SANN provides you with two random methods for initializing weights using the normal and uniform distributions. The normal method initializes the weights using normally distributed values, within a range whose mean is zero and standard deviation equal to one. On the other hand, the uniform method assigns weight values in the range 0 and 1. Neural Network training - learning by examples A neural network on its own cannot be used for making predictions unless it is trained on some examples known as training data. The training data usually consists of input-target pairs which are presented one by one to the network during training. You may view the input instances as “questions” and the target values as “answers”. Therefore each time a neural Teradata Warehouse Miner User Guide - Volume 3 151 Chapter 1: Analytic Algorithms Neural Networks network is presented with an input-target pair it is effectively told the answer for a given question. Nonetheless, at each instance of this presentation the neural network is required to make a guess using the current state (i.e. value) of the weights, and its performance is assessed using a criterion known as the error function. If the performance was not adequate, the network weights are adjusted to produce the right (or more correct answer) as compared to the previous attempt. In general, this learning process is noisy to some extent (i.e. the network answers my sometimes be more accurate in the previous cycle of training compared to the current one), but on the average the errors reduce in size as the network learning improves. The adjustment of the weights is usually carried out using a training algorithm, which like a teacher, teaches the neural network how to adapt its weights in order to make better predictions for each set of input-target pair in the dataset. The above steps are known as training. Algorithmically it is carried out using the following sequence of steps: 1 Present the network with an input-target pair. 2 Compute the predictions of the network for the targets. 3 Use the error function to calculate the difference between the predictions (output) of the network and the target values. 4 Continue with steps 1 and 2 until all input-target pairs are presented to the network. 5 Use the training algorithm to adjust the weights of the networks so that it gives better predictions for each and every input-target. Note that steps 1-5 form one training cycle or iteration. The number of cycles needed to train a neural network model is not known a priori, but can be determined as part of the training process. Repeat steps 1 to 5 again for a number of training cycles or iterations until the network starts producing sufficiently accurate outputs (i.e. outputs which are close enough to the targets given their input values). Steps 1 through 5 form one training cycle. A typical neural network training process consists of 100’s of cycles. The error function As discussed above, the error function is used to evaluate the performance of a neural networks during training. It is like an examiner who assesses the performance of a student. The error function measures how close the network predictions are to the targets and, hence, how much weight adjustment should be applied by the training algorithm in each iteration. Thus the error function is the eyes and ears of the training algorithm as to how well a network performs given its current state of training (and hence how much adjustment should be made to the value of its weights). All error functions used for training neural networks must provide some sort of distance measure between the targets and predictions at the location of the inputs. One common approach is to use the sum-squares error function. In this case the network learns a discriminant function. The sum-of-squares error is simply given by the sum of differences between the target and prediction outputs defined over the entire training set. Thus: 152 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks N is the number of training cases and yi is the prediction (network outputs) of the target value ti and target values of the ith datacase. It is clear that the bigger the difference between prediction of the network and the targets the higher the error value which means more weight adjustment is needed by the training algorithm. N yi – ti E sos = 2 i–1 The sum-of-squares error function is primarily used for regression analysis but it can also be used in classification tasks. Nonetheless, a true neural network classifier must have an error function other than sum-of-squares, namely cross entropy error function. It is with the use of this error function together with the softmax output activation function that we can interpret the outputs of a neural network as class membership probabilities. The cross entropy error function is given by: N yi E CE = – t i ln ---- ti i–1 which assumes that the target variables are derived from a multinomial distribution. This is in contrast to the sum-of-squares error which models the distribution of the targets as a normal probability density function. The training algorithm Neural networks are highly nonlinear tools which are usually trained using iterative techniques. The most recommended techniques for training neural networks are the BFGS and Scaled Conjugate Gradient algorithms (see Bishop 1995). These methods perform significantly better than the more traditional algorithms such as Gradient Descent, but they are, generally speaking, more memory intensive and computationally demanding. Nonetheless, these techniques may require a smaller number of iterations to train a neural network given their fast convergence rate and more intelligent search criterion. Training multilayer perceptron neural networks SANN provides several options for training MLP neural networks. These include BFGS, Scaled Conjugate and Gradient Descent. Training radial basis function neural networks The method used to train radial basis function networks is fundamentally different from that employed for MLPs. This mainly is due to the nature of the RBF networks with their hidden neurons (basis functions) forming a Gaussian mixture model which estimates the probability density of the input data (see Bishop 95). For RBF with linear activation functions the training process involves two stages. In the first part we fix the location and radial spread of the basis functions using the input data (no targets are considered at this stage). In the second stage we fix the weights connecting the radial functions to the output neurons. For identity Teradata Warehouse Miner User Guide - Volume 3 153 Chapter 1: Analytic Algorithms Neural Networks output activation function this second stage of training involves a simple matrix inversion. Thus it is exact and does not require an iterative process. The linear training, however, holds only when the error function is sum-of-squares and the output activation functions are the identity. If these requirements are not met, as in the case of cross-entropy error function and output activation functions other then the identity, we have to resort to an iterative algorithm, e.g. BFGS, to fix the hidden-output layer weights in order to complete the training of the RBF neural network. Generalization and performance The performance of neural networks is measured by how well they can predict unseen data (an unseen dataset is one not used during training). This is known as generalization. The issue of generalization is actually one of the major concerns when training neural networks. It is known as the tendency to overfit the training data accompanied by the difficulty in predicting new data. While one can always fine-tune (overfit) a sufficiently large and flexible neural network to achieve a perfect fit (viz. zero training error), the real issue here is how to construct a network which is capable of predicting new data well. As it turns out there is a relation between overfitting the training data and poor generalization. Thus when training neural networks one must take the issue of performance and generalization into account. Test data and early stopping The following figure shows a schematic of neural network training with early stopping. The network is repeatedly trained for a number of cycles so long as the test error is on the decrease. When the test error starts to increase training is halted. Figure 76: Neural Network Training with early stopping (schematic) There are several techniques to combat the problem of overfitting and tackling the generalization issue. The most popular ones involve the use of a test data. Test data is a holdout sample which will never be used in training. Instead it will be used as a means of validating how well a network makes progress in modeling the input-target relationship as training continues. Most work on assessing performance in neural modeling concentrates on approaches to test data. A neural network is optimized using a training set. A separate test set is used to halt training to mitigate overfitting. The process of halting of neural network 154 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks training to prevent overfitting and improving the generalization ability is known as “early stopping”. This technique slightly modifies the training algorithm to: 1 Present the network with an input-target pair from the training set. 2 Compute the predictions of the network for the targets. 3 Use the error function to calculate the difference between the predictions (output) of the network and the target values. 4 Continue with steps 1 and 2 until all input-target pairs from the training set are presented to the network. 5 Use the training algorithm to adjust the weights of the networks so that it gives better predictions for each and every input-target. 6 Pass the entire test set to the network, make predictions and compute the value of network test error. 7 Compare the test error with the one from the previous iteration. If the error keeps decreasing continue training, otherwise stop training. Note that the number of cycles needed to train a neural network model with test data and early stopping may vary. In theory we would continue training the network for as many cycles as needed so long as the test error is on the decrease. Validation data Sometimes the test data alone may not be sufficient proof of good generalization ability of a trained neural network. For example, it is entirely possible that a good performance on the test sample may actually be just a coincidence. To make sure that this is not the case, often we use another set of data known as the validation sample. Just as like the test sample, a validation sample is never used for training the neural network. Instead it is used at the end of training as an extra check on the performance of the model. If the performance of network was found to be consistently good on both the test and validation samples then it is reasonable to assume that the network generalizes well on unseen data. Regularization Besides the use of test data for early stopping, another technique frequently used for improving the generalization of neural networks is known as regularization. The method involves adding a term to the error function which generally penalizes (discourages) large weight values. One of the most common choices of regularization is known as weight decay (Bishop 1995). Weight decay works by modifying the network's error function to penalize large weights by adding an additional term Ew (same applied to the cross-entropy error function): E = E sos + E w T E w = ---w w 2 where is the weight decay constant and w are the network weights (biases excluded). The larger , the more the weights are penalized. Consequently, too large a weight decay constant Teradata Warehouse Miner User Guide - Volume 3 155 Chapter 1: Analytic Algorithms Neural Networks may damage network performance by encouraging underfitting, and experimentation is generally needed to determine an appropriate weight decay factor for a particular problem domain. The generalization ability of the network can depend crucially on the decay constant. One approach to choosing the decay constant is to train several networks with different amounts of decay and estimate the generalization error for each; then choose the decay constant that minimizes the estimated generalization error. The above form will encourage the development of smaller weights, which tends to reduce the problem of overfitting by limiting the ability of the network to form large curvature, thereby potentially improving generalization performance of the network. The result is a network which compromises between performance and weight size. It should noted that the basic weight decay model above might not always be the most suitable way of imposing regularization. A fundamental consideration with weight decay is that different weight groups in the network usually require different decay constants. Although this may be problem dependent, it is often the case that a certain group of weights in the network may require different scale values for an effective modeling of the data. An example of such is the input-hidden and hidden-output weights. Therefore, SANN uses separate weight decay values for regularizing these two groups of weights. Pre and post processing of data All neurons in a neural network take numeric input and produce numeric output. The activation function of a neural unit can accept input values in any range and produces output in a strictly limited range. Although the input can be in any range, there is a saturation effect so that the unit is only sensitive to inputs within a fairly limited range. For example consider the logistic function. In this case, the output is in the range (0, 1), and the input is sensitive in a range not much larger than (-1, +1). Thus for a wide range of input values ranging outside (1, +1), the output of a logistic neuron is approximately the same. This saturation effect will severely limit the ability of a network from capturing the underlying input-target relationship. The above problem can be solved by limiting the numerical range of the original input and target variables. This is process is known as scaling, one of the most commonly used forms of preprocessing. SANN scales the input and target variables using linear transformations such that the original minimum and maximum of each and every variable is mapped to the range (0, 1). There are other important reasons for standardization of the variables. One is related to weight decay. Standardizing the inputs and targets will usually make the weight decay regularization more effective. Other reasons include the original variable scaling and units of measure. It is often the case that variables in the original dataset have substantially different ranges (i.e. different variances). This may have to do with the units of measurements or simply the nature of the variables themselves. The numeric range of a variable, however, may not be a good indication of the importance of that variable. Predicting future data and deployment A fully trained neural network can be used for making predictions on any future data with variables which are thought to have been generated by the same underlying relations and processes as the original set used to train the model. The ability to generalize is an important 156 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks feature of neural networks and the process of using neural networks for making predictions in the future is known as deployment. SANN generated models can be saved and re-deployed later using the Predictive Markup Model Language (PMML). (See “Neural Networks Scoring” on page 249 for more information). There is one issue which needs consideration, however, when deploying neural network models. One should not attempt to extrapolate, viz. present a neural network model with input values differing significantly from those used to train the network. This is known as extrapolation which is generally unwise and unsafe. Recommended textbooks • Bishop, C. (1995). Neural Networks for Pattern Recognition. Oxford: University Press. • Carling, A. (1992). Introducing Neural Networks. Wilmslow, UK: Sigma Press. • Fausett, L. (1994). Fundamentals of Neural Networks. New York: Prentice Hall. • Haykin, S. (1994). Neural Networks: A Comprehensive Foundation. New York: Macmillan Publishing. • Patterson, D. (1996). Artificial Neural Networks. Singapore: Prentice Hall. • Ripley, B.D. (1996). Pattern Recognition and Neural Networks. Cambridge University Press. Initiate a Neural Networks Function Use the following procedure to initiate a new Neural Networks analysis in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 77: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Analytics under Categories and then under Analyses double-click on Neural Networks: Teradata Warehouse Miner User Guide - Volume 3 157 Chapter 1: Analytic Algorithms Neural Networks Figure 78: Add New Analysis dialogue 3 This will bring up the Neural Networks dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Neural Networks - INPUT - Data Selection On the Neural Networks dialog click on INPUT and then click on data selection: Figure 79: Neural Network > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 158 Select Columns From a Single Table Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks • Available Databases (or Analyses) — All the databases (or analyses) available for input to Neural Networks. • Available Tables — All the tables available for the Neural Networks analysis. • Available Columns — All the columns available for the Neural Networks analysis. • Neural Network Style — Select the type of analysis to perform: regression or classification. This will constrain the types of variables selectable as input or output (independent or dependent) to conform to the respective type of Neural Networks analysis. • • Regression — Select this option when your dependent (output) variables of interest are continuous in nature (e.g., weight, temperature, height, length, etc.). • Classification — Select this option when your dependent (output) variables of interest are categorical in nature (e.g., gender). Note that for classification analysis, you can only specify one target. Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a triply split window. You can insert columns as Dependent or Continuous Independent or Categorical Independent columns. Make sure you have the correct portion of the window highlighted. The Dependent variable columns are the columns whose values are being predicted by the Neural Networks model. The user may choose to treat a categorical variable as either categorical or continuous but a continuous variable must be treated as continuous only. Therefore the Independent Categorical columns cannot be of numeric type. The Independent Continuous columns and the Dependent columns may be of any type. Neural Networks - INPUT - Network Types On the Neural Networks dialog click on INPUT and then click on Network Types: Figure 80: Neural Network > Input > Network Types Network Types Use these options to specify the type of network (MLP or RBF). For each selected type, you can also specify a range for the complexity (i.e., minimum and maximum number of hidden units) of the neural network models to be tried by the Automatic Network Search (ANS). Specify the complexity of networks to be tested in terms of a range of figures for the number of hidden units. Specifying the number of hidden units exactly (i.e., by setting the minimum equal to the maximum) may be beneficial if you know, or have good cause to suspect, the optimal number. In this case, it allows the Automatic Network Search (ANS) to concentrate its search algorithms. The wider the range of hidden units in the ANS search, the better the Teradata Warehouse Miner User Guide - Volume 3 159 Chapter 1: Analytic Algorithms Neural Networks chances of finding an optimal model. On the other hand, if you know the optimal complexity, simply set the minimum and maximum number of hidden units to that value. MLP Select the MLP check box to include multilayer perceptron networks in the network search. The multilayer perceptron is the most common form of network. It requires iterative training, which may be quite slow, but the networks are quite compact, execute quickly once trained, and in most problems yield better results than the other types of networks. • Minimum Hidden Units — Specify the minimum number of hidden units to be tried by the Automatic Network Search (ANS) when using MLP networks. • Maximum Hidden Units — Specify the maximum number of hidden units to be tried by the Automatic Network Search (ANS) when using MLP networks. RBF Select the RBF check box to include radial basis function networks in the network search. Radial basis function networks tend to be slower and larger than Multilayer Perceptrons, and often have a relatively inferior performance, but they train extremely quickly when they use the identity output activation functions. They are also usually less effective than multilayer perceptrons if you have a large number of input variables (they are more sensitive to the inclusion of unnecessary inputs). • Minimum Hidden Units — Specify the minimum number of hidden units to be tried by the Automatic Network Search (ANS) when using RBF networks. • Maximum Hidden Units — Specify the maximum number of hidden units to be tried by the Automatic Network Search (ANS) when using RBF networks. Neural Networks - INPUT - Network Parameters On the Neural Networks dialog click on INPUT and then click on network parameters: Figure 81: Neural Network > Input > Network Parameters On this screen select: • Network Options 160 • Networks to Train — Use this option to specify how many networks the Automatic Network Search (ANS) should perform. The larger the number of networks trained the more detailed is the search carried out by the ANS. It is recommended that you set the value for this option as large as possible depending on your hardware speed and resources. • Networks to Retain — Specifies how many of the neural networks tested by the Automatic Network Search (ANS) should be retained (for testing, and then insertion Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks into the current network set). Networks with the best performance (i.e., best correlation fit for regression and classification rate for classification analysis) will be retained. • Error Functions • SOS — Select SOS to generate networks using the sum of squares error function. This option is available for both regression and classification analysis. • Cross Entropy — Select Cross entropy to generate networks using the cross entropy error function. Such networks perform maximum likelihood optimization, assuming that the data is drawn from the multinomial family of distributions. Together with the use of Softmax as output activation functions this supports a direct probabilistic interpretation of network outputs as probabilities. This error function is only available for classification, not for regression. Note: When the Cross Entropy error function is used to train a neural network, the output activation functions will always be of type softmax. • Weight Decay — This parameter specifies the use of weight decay regularization, promoting the development of smaller weights. This tends to reduce the problem of overfitting, thereby potentially improving generalization performance of the network. Weight decay works by modifying the network's error function to penalize large weights, resulting in an error function that compromises between performance and weight size. Because too large a weight decay term may damage network performance unacceptably, experimentation is often needed to determine an appropriate weight decay factor in a particular problem domain. • Output Layer — Select this option to apply weight decay regularization to the hiddenoutput layer weights. Specify the minimum and maximum weight decay value for the output layer weights. • Hidden Layer — Select this option to apply weight decay regularization to the inputhidden layer weights (Not applicable to RBF networks). When minimum and maximum weight decay values are selected for the hidden layer weights, the ANS will search for the best weight parameters within the specified range. Neural Networks - INPUT - MLP Activation Functions On the Neural Networks dialog click on INPUT and then click on MLP activation functions: Figure 82: Neural Network > Input > MLP Activation Functions • Hidden Neurons — This is the set of activation functions available to be used for the hidden layer for MLP neural networks. For RBF neural networks, however. only Gaussian activation functions are allowed. • Identity — Uses the identity function. With this function, the activation level is passed on directly as the output. Teradata Warehouse Miner User Guide - Volume 3 161 Chapter 1: Analytic Algorithms Neural Networks • Logistic — Uses the logistic sigmoid function. This is an S-shaped (sigmoid) curve, with output in the range (0,1). • Tanh — Uses the hyperbolic tangent function (recommended), is a symmetric Sshaped (sigmoid) function with output in range (-1, +1), and often performs better than the logistic sigmoid function because of its symmetry. • Exp — Uses the exponential activation function. • Sin — Uses the standard sine activation function. Since it may be useful only when data is radially distributed, it is not selected by default. • Output Neurons — This is the set of activation functions available to be used for the outputs for MLP neural networks. For RBF neural networks, however, only the identity function is allowed. When the error is “Cross Entropy”, MLP and RBF output activation functions are softmax. • Identity — Uses the identity function (recommended). With this function, the activation level is passed on directly as the output. • Logistic — Uses the logistic sigmoid function. This is an S-shaped (sigmoid) curve, with output in the range (0,1). • Tanh — Uses the hyperbolic tangent function, is a symmetric S-shaped (sigmoid) function with output in range (-1, +1), and often performs better than the logistic sigmoid function because of its symmetry. • Exp — Uses the exponential activation function. • Sin — Uses the standard sine activation function. This may be useful only when the data is radially distributed. Therefore it is not selected by default. Neural Networks - INPUT - Sampling On the Neural Networks dialog click on INPUT and then click on sampling: Figure 83: Neural Network > Input > Sampling • Teradata Sampling — Specify the fraction of the data table to sample from the Teradata table to pass on to the Automatic Network Search engine. • Neural Networks Sampling — The performance of a neural network is measured by how well it generalizes to unseen data (how well it predicts data not used during training). The issue of generalization is one of the major concerns when training neural networks. When the training data have been overfit (fit so completely that even the random noise within a particular data set is reproduced), it is difficult for the network to make accurate predictions using new data. A way to reduce this problem is to split the data into two (or three) subsets: a training sample, a testing sample and a validation sample. These samples can then be used to (1) train the network, (2) cross verify (or test) the performance of the training algorithms as they run, and (3) perform an final validation test to determine how well the network predicts “new” data. The assignment of the cases to the subsets can be 162 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks done randomly or based upon a special subset variable in the data set. Cases will be randomly assigned to subsets based on specified percentages with the total percentage summing to more than 0 and less or equal 100. To not split the data into subsets, enter a 100 in the Train sample size (%) field. Note, however, that the use of the test sample is strongly recommended to aid with training the networks. • Train Sample Size — Specify the percent of valid cases to use in the training sample. Default is 80%. • Test Sample Size — Randomly assign cases to a test sample, specifying the percentage of cases to use. Default is 20%. • Validation Sample Size — Randomly assign cases to a validation sample, specifying the percentage of cases to use. Default is 0%. • Seed for Sampling — The positive integer used as the seed for a random number generator that produces the random sub samples from the data. By changing the seed you can end up with different data cases in the train, test and validation samples (for each new analysis). Default is 1000. Run the Neural Networks After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Neural Networks The results of running the Teradata Warehouse Miner Neural Networks analysis include a variety of statistical reports on the individual variables and generated model as well as barcharts. All of these results are outlined below. On the Neural Networks dialog, click on RESULTS (note that the RESULTS tab will be grayedout/disabled until after the analysis is completed) to view results. Result options are as follows: Neural Network Reports • Neural Network Summary — For categorical analyses, this report gives the model name, training performance, test performance, training algorithm, error function, type of hidden activation, and type of output activation. For regression analysis, it gives the model name, training performance, test performance, training error, test error, training algorithm, error function, type of hidden activation, and type of output activation. • Correlation Coefficients (Regression only) — This report is a spreadsheet of correlation coefficients for each model. Teradata Warehouse Miner User Guide - Volume 3 163 Chapter 1: Analytic Algorithms Neural Networks • Data Statistics — This report contains some statistics (minimum, maximum, mean and standard deviation) of the input and target variables for training, testing, and validation samples. • Weights and Thresholds — This report is a spreadsheet of weights and thresholds for each model. • Sensitivity Analysis — A sensitivity analysis is displayed for each model in a spreadsheet. Sensitivity analysis rates the importance of the models' input variables. • Confusion Matrix (Classification only) — A confusion matrix is displayed for each model in a spreadsheet. This is a detailed breakdown of misclassifications. The observed class is displayed at the top of the matrix, and the predicted class down the side; each cell contains a number showing how many cases that were actually of the given observed class were assigned by the model to the given predicted class. In a perfectly performing model, all the cases are counted in the leading diagonal. • Classification Summary (Classification only) — A classification summary is displayed for each model in a spreadsheet. This gives the total number of observations in each class of the target, the number of correct and incorrect predictions for each class, and the percentage of correct and incorrect predictions for each class. This information is provided for each network. • Confidence (Classification only) — A confidence matrix is displayed for each model in a spreadsheet. Confidence levels will be displayed for each model. Pointwise Sensitivity Analysis (Regression with no categorical inputs only) • Pointwise Sensitivity — Generates a separate spreadsheet of model sensitivities for each model. Model sensitivities are values that indicate how sensitive the output of a neural network is to a given input at a particular location of the input. These sensitivity values are actual first-order derivatives evaluated at specific centile points for each input. For each input the derivative is taken with respect to the target at ten evenly spaced locations with the observed minimum and maximum values serving as end points. Other input variables are set to their respective means during this calculation. A separate spreadsheet is also generated for each dependent (target) variable as well. Note this option is available only for regression analyses with no categorical inputs. Neural Network Graphs Note: For more than one target (dependent variable), only the first will be available in graphs. • X-axis/Y-axis/Z-axis — Use the X-axis, Y-axis, and Z-axis list boxes to select a quantity to plot on the respective axis. Available graph types are dependent on the number of selections you make with these list boxes. For example, if you want to generate a 3D surface plot, you must select a value in each list box. By default, values are selected in the X-axis and Y-axis list box enabling you to create histograms (for the X-axis variables) or 2D scatter plots (for the X-axis and Y-axis variables). • Target — Select Target to plot the target that has been selected in the Target variable list on the selected axis. 164 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks • Output — Select Outputs to plot the output (or predicted value) of the target that has been selected in the Target variable list on the selected axis. • Residual — Select Residual to plot the residual value (for the selected target variable) on the axis. (regression only) • Std. Residual — Select Std. Residual to plot the standardized residual value (for the selected target variable) on the axis. (regression only). • Abs. Residual — Select Abs. Residual to plot the absolute value of the residual (for the selected target variable) on the axis. (regression only) • Square Residual — Select Square Residual to plot the squared residual value (for the selected target variable) on the axis. (regression only) • Accuracy — Select Accuracy to plot the accuracy (incorrect or correct) of the prediction on the selected axis. (classification only) • Conf — For classification type analyses, the confidence level for each category of the target can be selected and plotted on the axis. • Input variables — Each input variable is listed by name and is also available for selection. • Histogram of X — Click the Histogram of X button to generate a histogram of the quantity selected in the X-axis list box. When there is more than one active network, individual histograms will be generated for each network, when applicable. For example, if you select Residual in the X-axis box, then click Histograms of X, a histogram will be generated for each of the networks in the Active neural networks grid. • X and Y — Click the X and Y button to generate a 2D scatter plot of the variables selected in the X-axis and Y-axis list boxes. When there is more than one active network, a multiple scatter plot will be generated that plots the selected values for all networks, where applicable. For example, if you select Target in the X-axis box and Output in the Yaxis box, then click the X and Y button, only one scatter plot will be generated. It will contain a Target by Output plot for each of the active networks. • X, Y and Z — Click the X, Y and Z button generate a 3D surface plot of the variables selected in the X-axis, Y-axis, and Z-axis list boxes. When there is more than one active network, an individual surface plot will be generated for each network, when applicable. For example, if there are three active networks, a surface plot will be generated for each network. Lift Charts (Classification models only). These charts may be used to evaluate and compare the utility of the model for predicting the different categories or classes for the categorical target variable. Select the option that specifies the type of chart and the scaling for the chart you wish to compute. • Category — Select the response category for which to compute the gains and/or lift charts. You can chose to produce lift charts for a single or all categories. • Gains chart — Select this option button to compute a gains chart, which shows the percent of observations correctly classified into the chosen category (see Category of response) when taking the top x percent of cases from the sorted (by classification probabilities) data file. For example, this chart can show that by taking the top 20 percent (shown on the Teradata Warehouse Miner User Guide - Volume 3 165 Chapter 1: Analytic Algorithms Neural Networks x-axis) of cases classified into the respective category with the greatest certainty (maximum classification probability), you would correctly classify almost 80 percent of all cases (as shown on the vertical y-axis of the plot) belonging to that category in the population. In this plot, the baseline random classification (selection of cases) would yield a straight line (from the lower-left to the upper-right corner), which can serve as a comparison to gauge the utility of the respective models for classification. • Lift chart (resp %) — Select this option to compute a lift chart where the vertical y-axis is scaled in terms of the percent of all cases belonging to the respective category. As in the gains chart, the x-axis denotes the respective top x percent of cases from the sorted (by classification probabilities) data file. • Lift chart (lift value) — Select this option to compute a lift chart where the vertical y-axis is scaled in terms of the lift value, expressed as the multiple of the baseline random selection model. For example, this chart can show that by taking the top 20 percent (shown on the x-axis) of cases classified into the respective category with the greatest certainty (maximum classification probability), you would end up with a sample that has almost 4 times as many cases belonging to the respective category when compared to the baseline random selection (classification) model. • Cumulative — Show in the chosen lift and gains charts the cumulative percentages, lift values, etc. Clear this check box to show the simple (non-cumulative) values. • Lift Graphs — Creates the chart according to the options above. Tutorial - Neural Networks Tutorial 1: Performing Regression with Fictitious Banking Data For this example, we will use twm_customer_analysis, a fictitious banking dataset. The following is an example of using neural networks analysis regression. Here, cc_rev (credit card revenue) is predicted in terms of 20 independent variables, some continuous and some categorical. Starting the Analysis After connecting to the appropriate Teradata database: 1 166 Starting from the Input > Data Selection menu, select “Table” as Input Source, teraminer as the database, twm_customer_analysis as the input table and “Regression” as Neural Network Style. As Categorical Dependent Columns, select cc_rev, as Continuous Independent Columns select variables income, age, years_with_bank, nbr_children, avg_ cc_bal, avg_ck_bal, avg_sv_bal, avg_cc_tran_amt, avg_cc_tran_cnt, avg_ck_tran_amt, avg_ck_tran_cnt, avg_sv_tran_amt, and avg_sv_tran_cnt, and as Categorical Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Independent Columns select variables female, single, married, separated, ccact, ckacct, and svacct. Figure 84: Neural Network Tutorial 1: Data Selection Tab 2 Next, select the network types tab, which also includes network complexity, or number of hidden units, and click the button, “Load Defaults for Editing”. Teradata Warehouse Miner User Guide - Volume 3 167 Chapter 1: Analytic Algorithms Neural Networks Figure 85: Neural Network Tutorial 1: Network Types Tab The ANS can be configured to train both multilayer perceptron (MLP) networks and radial basis functions (RBF) networks. The multilayer perceptron is the most common form of network. It requires iterative training, which may be relatively slow, but the networks are quite compact, execute quickly once trained, and in most problems yield better results than the other types of networks. Radial basis function networks tend to be larger and hence slower than multilayer perceptrons, and often have a relatively inferior performance, but they train extremely quickly provided they use SOS error and linear output activation functions. They are also usually less effective than multilayer perceptrons if you have a large number of input variables (they are more sensitive to the inclusion of unnecessary inputs). Note that RBF networks are not appropriate for models that contain categorical inputs, so the RBF option is not available when categorical inputs are included in the model, as in this case. • 168 Network complexity (number of hidden units). One particular issue to which you need to pay attention is the number of hidden units (network complexity). For example, if you run ANS several times without producing any good networks, you may want to consider increasing the range of network complexity tried by ANS. Alternatively, if you believe that a certain number of neurons is optimal for your problem, you may then exclude the complexity factor from the ANS algorithm by simply setting the Min. hidden units equal to the Max. hidden units. This way you will help the ANS to concentrate on other network parameters in its search for the best network architecture and specifications, which unlike the number of hidden units, you do not know a priori. Note that network complexity is set separately for each network type. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks 3 Next, select the network parameters tab, which also includes error function and weight decay. Figure 86: Neural Network Tutorial 1: Network Parameters Tab • Networks to train, networks to retain. The number of networks that are to be trained and retained can be modified. You can specify any number of networks you may want to generate (the only limits are the resources on your machine) and choose to retain any number of them when training is over. If you want to retain all the models you train, set the value in Networks to train equal to the Networks to retain. However, often it is better to set the number of networks to retain to a smaller value than the number of networks to train. This will result in TWM Neural Networks retaining a subset of those networks that perform best on the data set. The ANS is a search algorithm that helps you create and test neural networks for your data analysis and prediction problems. It designs a number of networks to solve the problem, copies these into the current network set, and then selects those networks that perform best. For that reason, it is recommended that you set the value in Networks to train to as high as possible, even though it may take some time for TWM Neural Networks to complete the computation for data sets with many variables and data cases and/or networks with a large number of hidden units. This configures TWM Neural Networks to thoroughly search the space of network architectures and configurations and select the best for modeling the training data. Teradata Warehouse Miner User Guide - Volume 3 169 Chapter 1: Analytic Algorithms Neural Networks 4 • Error function. Specifies the error function to be used in training the networks. Because the analysis is regression, the SOS (sum-of-squares) error is the only option available since Cross Entropy is exclusively used for classification tasks. • Weight Decay. Use the default selection for Weight decay, which specifies use of weight decay regularization. • Use weight decay (hidden layer). Use the default selections for output layer weight decay, including minimum and maximum values. • Use weight decay (output layer). Use the default selections for hidden layer weight decay, including minimum and maximum values. Next, select the MLP Activation Functions tab. • MLP activation functions. This is a list of activation functions available for hidden and output layers of MLP networks. Figure 87: Neural Network Tutorial 1: MLP Activation Functions Tab Although most of the default configurations for the ANS are calculated from properties of the data, it is sometimes necessary to change these configurations to something other than the default. For example, you may want the search algorithm to include the sine function (not included by default) as a possible hidden and/or output activation function. This might prove useful when your data are radially distributed. Alternatively, sometimes you might know (from previous experience) that networks with tanh hidden activations might not do so well for your particular data set. In this case you can simply exclude this choice of activation function by clearing the Tanh check box. 170 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks You can specify activation functions for hidden and output neurons in a MLP network. These options do not apply to RBF networks. Note that you can also restrict the ANS from searching for best hidden and/or output activation functions by selecting only one option among the many that are available. For example, if you set the choice of hidden activations to Logistic, the ANS will then produce networks with this type of activation function only. Generally speaking, however, you should only restrict the ANS search parameters when you have a logical reason to do so. Unless you have a priori information about your data, you should make the ANS search parameters (for any network property) as wide as possible. 5 Finally, select the Sampling tab. Figure 88: Neural Network Tutorial 1: Sampling tab The performance of a neural network is measured by how well it generalizes to unseen data (i.e., how well it predicts data that was not used during training). The issue of generalization is actually one of the major concerns when training neural networks. When the training data have been overfit (i.e., been fit so completely that even the random noise within the particular data set is reproduced), it is difficult for the network to make accurate predictions using new data. One way to combat this problem is to split the data into two (or three) subsets: a training sample, a testing sample and a validation sample. These samples can then be used to (1) train the network, (2) cross verify (or test) the performance of the training algorithms as they run, and (3) perform an final validation test to determine how well the network predicts “new” data. Teradata Warehouse Miner User Guide - Volume 3 171 Chapter 1: Analytic Algorithms Neural Networks • Enable Teradata Sampling. The most efficient method of sampling a large dataset is the use of Teradata’s internal sampling function. Checking this box and entering the sampling fraction will automatically select the desired proportion of the target dataset to pass on to the Neural Network sampling option below. • Neural Networks Sampling. Percentages for each of the training, test, and validation sets are specifiable in this window. The seed for sampling may also be changed from its default value of 1000. Automatic Network Building TWM provides a neural network search/building strategy which automatically generates your models, Automatic Network Search (ANS). ANS creates neural networks with various settings and configurations with minimal user effort. ANS first creates a number of networks which solve the problem and then chooses the best networks representing the relationship between the input and target variables. 1 Click the execute button. This will trigger the Neural networks training. Training progress will be shown at the bottom of the screen. Once the training is completed, the TWM Neural Networks - Results button will become visible. 2 Click the Results button to show the Reports and Graph Screen. Figure 89: Neural Networks Tutorial 1: Results tab - Reports button 172 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks • Reviewing the results. The neural network summary enables you to quickly compare the training and testing performance for each of the selected networks and provides additional summary information about each model including the algorithm used in training, the error function and activation functions used for the hidden and output layers. When a Validation subset is specified (on the Input Sampling tab), performance for that subset is also displayed in the Neural Network Summary. Figure 90: Neural Networks Tutorial 1: Reports - Neural Network Summary • Correlation Coefficients. Click this button to view the correlation coefficients of the networks. Teradata Warehouse Miner User Guide - Volume 3 173 Chapter 1: Analytic Algorithms Neural Networks Figure 91: Neural Networks Tutorial 1: Reports - Correlation Coefficients • 174 Data statistics. Click this button to create a spreadsheet containing some statistics (minimum, maximum, mean and standard deviation) of the input and target variables for the training, testing, and validation samples. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 92: Neural Networks Tutorial 1: Reports - Data Statistics • Weights. Click the Weights and Thresholds button to display a spreadsheet of weights and thresholds for each model in the Active neural networks grid. Teradata Warehouse Miner User Guide - Volume 3 175 Chapter 1: Analytic Algorithms Neural Networks Figure 93: Neural Networks Tutorial 1: Reports - Weights • Sensitivity Analysis. Sensitivity Analysis gives you some information about the relative importance of the variables used in a neural network. In sensitivity analysis, TWM Neural Networks tests how the neural network outputs would change should a particular input variable were to change. There are two types of sensitivity analysis in TWM Neural Networks, namely local and global sensitivities. The local sensitivity measures how sensitive the output of a neural network is to a particular value of an input variable. The larger the change the more influential that input is. By contrast, the global sensitivity measures the average (global) importance of the network outputs with respect to the individual inputs. Sensitivity analysis actually measures only the importance of variables in the context of a particular neural model. Variables usually exhibit various forms of interdependency and redundancy. If several variables are correlated, then the training algorithm may arbitrarily choose some combination of them and the sensitivities may reflect this, giving inconsistent results between different networks. It is usually best to run sensitivity analysis on a number of networks, and to draw conclusions only from consistent results. Nonetheless, sensitivity analysis is useful in helping you to understand how important variables are. 176 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 94: Neural Networks Tutorial 1: Reports - Sensitivity Analysis • Predictions. See “Neural Networks Scoring” on page 249. • Graphs. Next, click on the Graph tab. The options on this tab enable you to create histograms, 2D scatter plots, and 3D surface plots using targets, predictions, residuals and inputs. Teradata Warehouse Miner User Guide - Volume 3 177 Chapter 1: Analytic Algorithms Neural Networks Figure 95: Neural Networks Tutorial 1: Results tab - Graph button For example, you can review the distribution of the target variable cc_rev. Select Target in the X-axis list box and click the Histograms of X button. 178 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 96: Neural Networks Tutorial 1: Graph - Histogram For a scatter plot of target vs. output, select target in the X-axis list and output in the Yaxis list, and click the X and Y button. Teradata Warehouse Miner User Guide - Volume 3 179 Chapter 1: Analytic Algorithms Neural Networks Figure 97: Neural Networks Tutorial 1: Graph - Target Output In the Select Networks to Graph window, when multiple networks are selected by checkmarks in the model name column, the scatter plots of all the selected networks are overlaid. This enables you to compare the values for all networks. Similarly, three dimensional graphs may be generated of variables relationships by selecting variables for X, Y, and Z axes and clicking the “X, Y and Z” button. 180 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 98: Neural Networks Tutorial 1: Graph - X, Y and Z Unique models, best models, good models. If you have not worked with neural networks for building predictive models, it is important to remember that these are “general learning algorithms,” not statistical estimation techniques. That means that the models that are generated may not necessarily be the best models that could be found, nor is there a single best model. In practice, you will often find several models that appear of nearly identical quality. Each model can be regarded, in this case, as a unique solution. Note that even models with the same number of hidden units, hidden and output activation function, etc., may actually have different predictions and hence different performance. This is due to the nature of neural networks as highly nonlinear models capable of producing multiple solutions for the same problem. Tutorial 2: Performing Classification with Fictitious Banking Data For this example, we will use twm_customer_analysis, a fictitious banking dataset. The following is an example of using neural networks analysis classification. Here, ccacct (has credit card, 0 or 1) is predicted in terms of 16 independent variables, from income to avg_sv_ tran_cnt. Starting the Analysis After connecting to the appropriate Teradata database, from the Input/Data Selection menu: 1 Select “Table” as Input Source, teraminer as the database, twm_customer_analysis as the input table and “Classification” as Neural Network Style. As Categorical Dependent Columns, select ccact, as Continuous Independent Columns select variables income, age, Teradata Warehouse Miner User Guide - Volume 3 181 Chapter 1: Analytic Algorithms Neural Networks years_with_bank, nbr_children, avg_ck_bal, avg_sv_bal, avg_ck_tran_amt, avg_ck_ tran_cnt, avg_sv_tran_amt, and avg_sv_tran_cnt, and as Categorical Independent Columns select variables female, single, married, separated, ckacct, and svacct. Figure 99: Neural Networks Tutorial 2: Data Selection tab 2 182 Next, select the network types tab, which also includes network complexity, or number of hidden units, and click the button, “Load Defaults for Editing”. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 100: Neural Networks Tutorial 2: Network Types tab The ANS can be configured to train both multilayer perceptron (MLP) networks and radial basis functions (RBF) networks. The multilayer perceptron is the most common form of network. It requires iterative training, which may be relatively slow, but the networks are quite compact, execute quickly once trained, and in most problems yield better results than the other types of networks. Radial basis function networks tend to be larger and hence slower than multilayer perceptrons, and often have a relatively inferior performance, but they train extremely quickly provided they use SOS error and linear output activation functions. They are also usually less effective than multilayer perceptrons if you have a large number of input variables (they are more sensitive to the inclusion of unnecessary inputs). Note that RBF networks are not appropriate for models that contain categorical inputs, so the RBF option is not available when categorical inputs are included in the model, as in this case. • Network complexity (number of hidden units). One particular issue to which you need to pay attention is the number of hidden units (network complexity). For example, if you run ANS several times without producing any good networks, you may want to consider increasing the range of network complexity tried by ANS. Alternatively, if you believe that a certain number of neurons is optimal for your problem, you may then exclude the complexity factor from the ANS algorithm by simply setting the Min. hidden units equal to the Max. hidden units. This way you will help the ANS to concentrate on other network parameters in its search for the best network architecture and specifications, which unlike the number of hidden units, you do not know a priori. Note that network complexity is set separately for each network type. Teradata Warehouse Miner User Guide - Volume 3 183 Chapter 1: Analytic Algorithms Neural Networks 3 Next, select the network parameters tab, which also includes error function and weight decay. Figure 101: Neural Networks Tutorial 2: Network Parameters tab • Networks to train, networks to retain. The number of networks that are to be trained and retained can be modified. You can specify any number of networks you may want to generate (the only limits are the resources on your machine) and choose to retain any number of them when training is over. If you want to retain all the models you train, set the value in Networks to train equal to the Networks to retain. However, often it is better to set the number of networks to retain to a smaller value than the number of networks to train. This will result in TWM Neural Networks retaining a subset of those networks that perform best on the data set. The ANS is a search algorithm that helps you create and test neural networks for your data analysis and prediction problems. It designs a number of networks to solve the problem, copies these into the current network set, and then selects those networks that perform best. For that reason, it is recommended that you set the value in Networks to train to as high as possible, even though it may take some time for TWM Neural Networks to complete the computation for data sets with many variables and data cases and/or networks with a large number of hidden units. This configures TWM Neural Networks to thoroughly search the space of network architectures and configurations and select the best for modeling the training data. 184 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks 4 • Error function. Specifies the error function to be used in training a network. Because the analysis is classification, the default is either SOS or Cross Entropy. In such cases, both error functions will be tried, and the best chosen by ANS. • Weight Decay. Use the default selection for Weight decay, which specifies use of weight decay regularization. • Use weight decay (hidden layer). Use the default selections for output layer weight decay, including minimum and maximum values. • Use weight decay (output layer). Use the default selections for hidden layer weight decay, including minimum and maximum values. Next, select the MLP Activation Functions tab. Figure 102: Neural Networks Tutorial 2: MLP Activation Functions tab • MLP activation functions. This is a list of activation functions available for hidden and output layers of MLP networks. Although most of the default configurations for the ANS are calculated from properties of the data, it is sometimes necessary to change these configurations to something other than the default. For example, you may want the search algorithm to include the sine function (not included by default) as a possible hidden and/or output activation function. This might prove useful when your data are radially distributed. Alternatively, sometimes you might know (from previous experience) that networks with tanh hidden activations might not do so well for your particular data set. In this Teradata Warehouse Miner User Guide - Volume 3 185 Chapter 1: Analytic Algorithms Neural Networks case you can simply exclude this choice of activation function by clearing the Tanh check box. You can specify activation functions for hidden and output neurons in a MLP network. These options do not apply to RBF networks. Note that you can also restrict the ANS from searching for best hidden and/or output activation functions by selecting only one option among the many that are available. For example, if you set the choice of hidden activations to Logistic, the ANS will then produce networks with this type of activation function only. Generally speaking, however, you should only restrict the ANS search parameters when you have a logical reason to do so. Unless you have a priori information about your data, you should make the ANS search parameters (for any network property) as wide as possible. 5 Finally, select the Sampling tab. Figure 103: Neural Networks Tutorial 2: Sampling tab The performance of a neural network is measured by how well it generalizes to unseen data (i.e., how well it predicts data that was not used during training). The issue of generalization is actually one of the major concerns when training neural networks. When the training data have been overfit (i.e., been fit so completely that even the random noise within the particular data set is reproduced), it is difficult for the network to make accurate predictions using new data. One way to combat this problem is to split the data into two (or three) subsets: a training sample, a testing sample and a validation sample. These samples can then be used to (1) train the network, (2) cross verify (or test) the 186 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks performance of the training algorithms as they run, and (3) perform an final validation test to determine how well the network predicts “new” data. • Enable Teradata Sampling. The most efficient method of sampling a large dataset is the use of Teradata’s internal sampling function. Checking this box and entering the sampling fraction will automatically select the desired proportion of the target dataset to pass on to the Neural Network sampling option below. • Neural Networks Sampling. Percentages for each of the training, test, and validation sets are specifiable in this window. The seed for sampling may also be changed from its default value of 1000. Automatic Network Building TWM provides a neural network search/building strategy which automatically generates your models, Automatic Network Search (ANS). ANS creates neural networks with various settings and configurations with minimal user effort. ANS first creates a number of networks which solve the problem and then chooses the best networks representing the relationship between the input and target variables. 1 Click the execute button. This will trigger the Neural networks training. Training progress will be shown at the bottom of the screen. Once the training is completed, the TWM Neural Networks - Results button will become visible. 2 Click the results button to show the Reports and Graph Screen. Teradata Warehouse Miner User Guide - Volume 3 187 Chapter 1: Analytic Algorithms Neural Networks Figure 104: Neural Networks Tutorial 2: Results tab - Reports button • 188 Reviewing the results. The neural network summary enables you to quickly compare the training and testing performance for each of the selected networks and provides additional summary information about each model including the algorithm used in training, the error function and activation functions used for the hidden and output layers. When a Validation subset is specified (on the Input Sampling tab), performance for that subset is also displayed in the Neural Network Summary. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 105: Neural Networks Tutorial 2: Results - Neural Network Summary • Data statistics. Click this button to create a spreadsheet containing some statistics (minimum, maximum, mean and standard deviation) of the input and target variables for the training, testing, and validation samples. Teradata Warehouse Miner User Guide - Volume 3 189 Chapter 1: Analytic Algorithms Neural Networks Figure 106: Neural Networks Tutorial 2: Reports - Data Statistics • 190 Weights. Click the Weights and Thresholds button to display a spreadsheet of weights and thresholds for each model in the Active neural networks grid. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 107: Neural Networks Tutorial 2: Reports - Weights • Sensitivity Analysis. Sensitivity Analysis gives you some information about the relative importance of the variables used in a neural network. In sensitivity analysis, TWM Neural Networks tests how the neural network would cope if each of its input variables were unavailable. TWM Neural Networks has facilities to automatically compensate for missing values (for classification analysis, casewise deletion of missing data is used). In sensitivity analysis, the data set is submitted to the network repeatedly, with each variable in turn treated as missing, and the resulting network error is recorded. If an important variable is removed in this fashion, the error will increase a great deal; if an unimportant variable is removed, the error will not increase very much. The spreadsheet shows, for each selected model, the ratio of the network error with a given input omitted to the network error with the input available. It also shows the rank order of these ratios for each input, which puts the input variables into order of importance. If the ratio is 1 or less, the network actually performs better if the variable is omitted entirely - a sure sign that it should be pruned from the network. We tend to interpret the sensitivities as indicating the relative importance of variables. However, they actually measure only the importance of variables in the context of a particular neural model. Variables usually exhibit various forms of interdependency and redundancy. If several variables are correlated, then the training algorithm may arbitrarily choose some combination of them and the sensitivities may reflect this, giving inconsistent results between different networks. It is usually best to run sensitivity analysis on a number of networks, and to draw conclusions only from Teradata Warehouse Miner User Guide - Volume 3 191 Chapter 1: Analytic Algorithms Neural Networks consistent results. Nonetheless, sensitivity analysis is extremely useful in helping you to understand how important variables are. Figure 108: Neural Networks Tutorial 2: Reports - Sensitivity Analysis • 192 Confusion matrix. Click the Confusion matrix button to generate a confusion matrix and classification summary for the categorical target. A confusion matrix gives a detailed breakdown of misclassifications. The observed class is displayed at the top of the matrix, and the predicted class down the side; each cell contains a number showing how many cases that were actually of the given observed class were assigned by the model to the given predicted class. In a perfectly performing model, all the cases are counted in the leading diagonal. A classification summary gives the total number of observations in each class of the target, the number of correct and incorrect predictions for each class, and the percentage of correct and incorrect predictions for each class. This information is provided for each active network. Note this option is only available for classification. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 109: Neural Networks Tutorial 2: Reports - Confusion Matrix Teradata Warehouse Miner User Guide - Volume 3 193 Chapter 1: Analytic Algorithms Neural Networks Classification Summary Figure 110: Neural Networks Tutorial 2: Reports - Classification Summary • Confidence levels. Click the Confidence button to display a spreadsheet of confidence levels for each case. Confidence levels will be displayed for each model. Note that this option is only available for classification problems. 194 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 111: Neural Networks Tutorial 2: Reports - Confidence Levels • Predictions. See “Neural Networks Scoring” on page 249. • Graphs. Next, click on the Graph tab. The options on this tab enable you to create histograms, 2D scatter plots, and 3D surface plots using targets, predictions, residuals and inputs. Teradata Warehouse Miner User Guide - Volume 3 195 Chapter 1: Analytic Algorithms Neural Networks Figure 112: Neural Networks Tutorial 2: Results tab - Graph button For example, you can review the distribution of the target variable ccact. Select Target in the X-axis list box and click the Histograms of X button. • 196 To review histograms of model accuracy (number correct, number incorrect), select Accuracy in the X-axis list box, and click the Histogram of X button. Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 113: Neural Networks Tutorial 2: Graph - Histogram • For a scatter plot of income vs. age, select income in the X-axis list and age in the Yaxis list, and click the X and Y button. Teradata Warehouse Miner User Guide - Volume 3 197 Chapter 1: Analytic Algorithms Neural Networks Figure 114: Neural Networks Tutorial 2: Graph - Income vs. Age • In the Select Networks to Graph window, when multiple networks are selected by checkmarks in the model name column, the scatter plots of all the selected networks are overlaid. This enables you to compare the values for all networks. • Similarly, three dimensional graphs may be generated of variables relationships by selecting variables for X, Y, and Z axes and clicking the “X, Y and Z” button. • Lift Charts. Lift Graphs may be generated of three different types, and may be either cumulative or non-cumulative. Choose the variable’s value or “All” and click the Lift Graphs button to see that variable value’s lift, or that of all variable values. For example: 198 Teradata Warehouse Miner User Guide - Volume 3 Chapter 1: Analytic Algorithms Neural Networks Figure 115: Neural Networks Tutorial 2: Graph - Lift Charts • Unique models, best models, good models. If you have not worked with neural networks for building predictive models, it is important to remember that these are “general learning algorithms,” not statistical estimation techniques. That means that the models that are generated may not necessarily be the best models that could be found, nor is there a single best model. In practice, you will often find several models that appear of nearly identical quality. Each model can be regarded, in this case, as a unique solution. Note that even models with the same number of hidden units, hidden and output activation function, etc., may actually have different predictions and hence different performance. This is due to the nature of neural networks as highly nonlinear models capable of producing multiple solutions for the same problem. Teradata Warehouse Miner User Guide - Volume 3 199 Chapter 1: Analytic Algorithms Neural Networks 200 Teradata Warehouse Miner User Guide - Volume 3 Chapter 2: Scoring Overview CHAPTER 2 Scoring What’s In This Chapter For more information, see these subtopics: 1 “Overview” on page 201 2 “Cluster Scoring” on page 201 3 “Tree Scoring” on page 209 4 “Factor Scoring” on page 219 5 “Linear Scoring” on page 228 6 “Logistic Scoring” on page 236 7 “Neural Networks Scoring” on page 249 Overview Model scoring in Teradata Warehouse Miner is performed entirely through generated SQL, executed in the database (although PMML based scoring generally requires that certain supplied User Defined Functions be installed beforehand). A scoring analysis is provided for every Teradata Warehouse Miner algorithm that produces a predictive model (thus excluding the Association Rules algorithm). Scoring applies a predictive model to a data set that has the same columns as those used in building the model, with the exception that the scoring input table need not always include the predicted or dependent variable column for those models that utilize one. In fact, the dependent variable column is required only when model evaluation is requested in the Tree Scoring, Linear Scoring and Logistic Scoring analyses. Cluster Scoring Scoring a table is the assignment of each row to a cluster. In the Gaussian Mixture model, the “maximum probability rule” is used to assign the row to the cluster for which its conditional probability is the largest. The model also assigns relative probabilities of each cluster to the row, so the soft assignment of a row to more than one cluster can be obtained. When scoring is requested, the selected table is scored against centroids/variances from the selected Clustering analysis. After a single iteration, each row is assigned to one of the previously defined clusters, together with the probability of membership. The row to cluster assignment is based on the largest probability. Teradata Warehouse Miner User Guide - Volume 1 201 Chapter 2: Scoring Cluster Scoring The Cluster Scoring analysis scores an input table that contains the same columns that were used to perform the selected Clustering Analysis. The implicit assumption in doing this is that the underlying population distributions are the same. When scoring is requested, the specified table is scored against the centroids and variances obtained in the selected Clustering analysis. Only a single iteration is required before the new scored table is produced. After clusters have been identified by their centroids and variances, the scoring engine identifies to which cluster each row belongs. The Gaussian Mixture model permits multiple cluster memberships, with scoring showing the probability of membership to each cluster. In addition, the highest probability is used to assign the row absolutely to a cluster. The resulting score table consists of the index (key) columns, followed by probabilities for each cluster membership, followed by the assigned cluster number (the cluster with the highest probability of membership). Initiate Cluster Scoring After generating a Cluster analysis (as described in “Cluster Analysis” on page 19), use the following procedure to initiate Cluster Scoring: 1 Click on the Add New Analysis icon in the toolbar: Figure 116: Add New Analysis from toolbar 2 202 In the resulting Add New Analysis dialog box, click on Scoring under Categories and then under Analyses double-click on Cluster Scoring: Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Cluster Scoring Figure 117: Add New Analysis > Scoring > Cluster Scoring 3 This will bring up the Cluster Scoring dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Cluster Scoring - INPUT - Data Selection On the Factor Scoring dialog click on INPUT and then click on data selection: Figure 118: Add New Analysis > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). Teradata Warehouse Miner User Guide - Volume 1 203 Chapter 2: Scoring Cluster Scoring 2 3 Select Columns From a Single Table • Available Databases — All available source databases that have been added through Connection Properties. • Available Tables — The tables available for scoring are listed in this window, though all may not strictly qualify; the input table to be scored must contain the same column names used in the original analysis. • Available Columns — The columns available for scoring are listed in this window. • Selected Columns • Index Columns — Note that the Selected Columns window is actually a split window for specifying Index and/or Retain columns if desired. If a table is specified as input, the primary index of the table is defaulted here, but can be changed. If a view is specified as input, an index must be provided. • Retain Columns — Other columns within the table being scored can be appended to the scored table, by specifying them here. Columns specified in Index Columns may not be specified here. Select Model Analysis — Select from the list an existing Cluster analysis on which to run the scoring. The Cluster analysis must exist in the same project as the Cluster Scoring analysis. Cluster Scoring - INPUT - Analysis Parameters On the Cluster Scoring dialog click on INPUT and then click on analysis parameters: Figure 119: Add New Analysis > Input > Analysis Parameters On this screen select: • Score Options • Include Cluster Membership — The name of the column in the output score table representing the cluster number to which an observation or row belongs can be set by the user. This column may be excluded by un-checking the selection box, but if this is done the cluster probability scores must be included. • • 204 Column Name — Name of the column that will be populated with the cluster numbers. Note that this can not have the same name as any of the columns in the table being scored. Include Cluster Probability Scores — The prefix of the name of the columns in the output score table representing the probabilities that an observation or row belongs to each cluster can be set by the user. A column is created for each possible cluster, adding the cluster number to this prefix (for example, p1, p2, p3). These columns may Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Cluster Scoring be excluded by un-checking the selection box, but if this is done the cluster membership number must be included. • Column Prefix — A prefix for each column generated (one per cluster) that will be populated with the probability scores. Note that the prefix used will have sequential numbers, beginning with 1 and incrementing for each cluster, appended to it. If the resultant column conflicts with a column in the table to be scored, an error will occur. Cluster Scoring - OUTPUT On the Cluster Scoring dialog click on OUTPUT: Figure 120: Cluster Scoring > Output On this screen select: • Output Table • Database name — The name of the database. • Table name — The name of the scored output table to be created-required only if a scoring option is selected. • Create output table using the FALLBACK keyword — If a table is selected, it will be built with FALLBACK if this option is selected • Create output table using the MULTISET keyword — This option is not enabled for scored output tables; the MULTISET keyword is not used. • Advertise Output — The Advertise Output option “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate the SQL for this analysis, but do not execute it — If this option is selected the analysis will only generate SQL, returning it and terminating immediately. Note: To create a stored procedure to score this model, use the Refresh analysis. Run the Cluster Scoring Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: Teradata Warehouse Miner User Guide - Volume 1 205 Chapter 2: Scoring Cluster Scoring • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Cluster Scoring The results of running the Teradata Warehouse Miner Cluster Scoring Analysis include a variety of statistical reports on the scored model. All of these results are outlined below. Cluster Scoring - RESULTS - reports On the Cluster Scoring dialog click RESULTS and then click on reports (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 121: Cluster Scoring > Results > Reports • Clustering Scoring Report • Iteration — When scoring, the algorithm performs only one iteration, so this value is always 1. • Log Likelihood — This is the log likelihood value calculated using the scored data, giving a measure of the effectiveness of the model applied to this data. • Diff — Since only one iteration of the algorithm is performed when scoring, this is always 0. • Timestamp — This is the day, date, hour, minute and second marking the end of scoring processing. Cluster Scoring - RESULTS - data On the Cluster Scoring dialog click RESULTS and then click on data (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 122: Cluster Scoring > Results > Data Results data, if any, is displayed in a data grid as described in the “RESULTS Tab” on page 80 of the Teradata Warehouse Miner User Guide (Volume 1). 206 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Cluster Scoring If a table was created, a sample of rows is displayed here - the size determined by the setting specified by Maximum result rows to display in Tools-Preferences-Limits. The following table is built in the requested Output Database by the Cluster Scoring analysis. Note that the options selected affect the structure of the table. Those columns in bold below will comprise the Unique Primary Index (UPI). Also note that there may be repeated groups of columns, and that some columns will be generated only if specific options are selected. Table 51: Output Database (Built by the Cluster Scoring analysis) Name Type Definition Key User Defined One or more unique-key columns, which default to the index, defined in the table to be scored (i.e. in Selected Tables). The data type defaults to the same as the scored table, but can be changed via Primary Index Columns and Types. Px (Default) FLOAT The probabilities that an observation or row belongs to each cluster if the Include Cluster Probability Scores option is selected. A column is created for each possible cluster, adding the cluster number to the prefix entered in the Column Prefix option. This prefix will be used for each column generated (one per cluster) that will be populated with the probability scores. Note that the prefix used will have sequential numbers, beginning with 1 and incrementing for each cluster, appended to it. (By default, the Column Prefix is p, so p1, p2, p3, etc. will be generated). These columns may be excluded by not selecting the Include Cluster Probability Scores option, but if this is done the cluster membership number must be included. Clusterno (Default) INTEGER The column in the output score table representing the cluster number to which an observation or row belongs can be set by the user. This column may be excluded by not selecting the Include Cluster Membership option, but if this is done the cluster probability scores must be included (see above). The name of the column defaults to “clusterno”, but this can be overwritten by entering another value in Column Name under the Include Cluster Membership option. Note that this can not have the same name as any of the index columns in the table being scored. The name entered can not exist as a column in the table being scored. Cluster Scoring - RESULTS - SQL On the Cluster Scoring dialog click RESULTS and then click on SQL (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 123: Cluster Scoring > Results > SQL Teradata Warehouse Miner User Guide - Volume 1 207 Chapter 2: Scoring Cluster Scoring The SQL generated for scoring is returned here, but only if the Output - Storage option to Generate the SQL for this analysis, but do not execute it was selected. When SQL is displayed here, it may be selected and copied as desired. (Both right-click menu options and buttons to Select All and Copy are available). Tutorial - Cluster Scoring In this example, the same table is scored as was used to build the cluster analysis model. Parameterize a Cluster Score Analysis as follows: • Selected Table — twm_customer_analysis • Include Cluster Membership — Enabled • Column Name — Clusterno • Include Cluster Probability Scores — Enabled • Column Prefix — p • Result Table Name — twm_score_cluster_1 • Index Columns — cust_id Run the analysis, and click on Results when it completes. For this example, the Cluster Scoring Analysis generated the following pages. A single click on each page name populates Results with the item. Table 52: Clustering Progress Iteration Log Likelihood Diff Timestamp 1 -24.3 0 Tue Jun 12 15:41:58 2001 Table 53: Data cust_id p1 p2 p3 clusterno 1362509 .457 .266 .276 1 1362573 1.12E-22 1 0 2 1362589 6E-03 5.378E-03 .989 3 1362693 8.724E-03 8.926E-03 .982 3 1362716 3.184E-03 3.294E-03 .994 3 1362822 .565 .132 .303 1 1363017 7.267E-02 .927 1.031E-18 2 1363078 3.598E-03 3.687E-03 .993 3 1363438 2.366E-03 2.607E-03 .995 3 1363465 .115 5.923E-02 .826 3 208 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Tree Scoring Table 53: Data cust_id p1 p2 p3 clusterno … … … … … … … … … … … … … … … Tree Scoring After building a model a means of deploying it is required to allow scoring of new data sets. The way in which Teradata Warehouse Miner deploys a decision tree model is via SQL. A series of SQL statements is generated from the metadata model that describes the decision tree. The SQL uses CASE statements to classify the predicted value. Here is an example of a statement: SELECT CASE WHEN(subset1 expression) THEN ‘Buy’ WHEN(subset2 expression) THEN ‘Do not Buy’ END FROM tablename; Note that Tree Scoring applies a Decision Tree model to a data set that has the same columns as those used in building the model (with the exception that the scoring input table need not include the predicted or dependent variable column unless model evaluation is requested). A number of scoring options including model evaluation and profiling rulesets are provided on the analysis parameters panel of the Tree Scoring analysis. Initiate Tree Scoring After generating a Decision Tree analysis (as described in “Decision Trees” on page 36) use the following procedure to initiate Tree Scoring: 1 Click on the Add New Analysis icon in the toolbar: Figure 124: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Scoring under Categories and then under Analyses double-click on Tree Scoring: Teradata Warehouse Miner User Guide - Volume 1 209 Chapter 2: Scoring Tree Scoring Figure 125: Add New Analysis > Scoring > Tree Scoring 3 This will bring up the Tree Scoring dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Tree Scoring - INPUT - Data Selection On the Tree Scoring dialog click on INPUT and then click on data selection: Figure 126: Tree Scoring > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 210 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Tree Scoring 2 Select Columns From a Single Table • Available Databases — All available source databases that have been added through Connection Properties. • Available Tables — The tables available for scoring are listed in this window, though all may not strictly qualify; the input table to be scored must contain the same column names used in the original analysis. • Available Columns — The columns available for scoring are listed in this window. • Selected Columns • Index Columns — Note that the Selected Columns window is actually a split window for specifying Index and/or Retain columns if desired. If a table is specified as input, the primary index of the table is defaulted here, but can be changed. If a view is specified as input, an index must be provided. • Retain Columns — Other columns within the table being scored can be appended to the scored table, by specifying them here. Columns specified in Index Columns may not be specified here. 3 Select Model Analysis 4 Select from the list an existing Decision Tree analysis on which to run the scoring. The Decision Tree analysis must exist in the same project as the Decision Tree Scoring analysis. Tree Scoring - INPUT - Analysis Parameters On the Tree Scoring dialog click on INPUT and then click on analysis parameters: Figure 127: Tree Scoring > Input > Analysis Parameters On this screen select: • Scoring Method • Score — Option to create a score table only. • Evaluate — Option to perform model evaluation only. Not available for Decision Tree models built using the Regression Trees option. • Evaluate and Score — Option to create a score table and perform model evaluation. Not available for Decision Tree models built using the Regression Trees option. • Scoring Options • Use Dependent variable for predicted value column name — Option to use the exact same column name as the dependent variable when the model is scored. This is the default option. Teradata Warehouse Miner User Guide - Volume 1 211 Chapter 2: Scoring Tree Scoring • Predicted Value Column Name — If above option is not checked, then enter here the name of the column in the score table which contains the estimated value of the dependent variable. • Include Confidence Factor — If this option is checked then the confidence factor will be added to the output table. The Confidence Factor is a measure of how “confident” the model is that it can predict the correct score for a record that falls into a particular leaf node based on the training data the model was built from. Example: If a leaf node contained 10 observations and 9 of them predict Buy and the other record predicts Do Not Buy, then the model built will have a confidence factor of .9, or be 90% sure of predicting the right value for a record that falls into that leaf node of the model. If the Include validation table option was selected when the decision tree model was built, additional information is provided in the scored table and/or results depending on the scoring option selected. If Score Only is selected, a recalculated confidence factor based on the original validation table is included in the scored output table. If Evaluate Only is selected, a confusion matrix based on the selected table to score is added to the results. If Evaluate and Score is selected, then a confusion matrix based on the selected table to score is added to the results and a recalculated confidence factor based on the selected table to score is included in the scored output table. • Targeted Confidence (Binary Outcome Only) — Models built with a predicted variable that has only 2 outcomes can add a targeted confidence value to the output table. The outcomes of the above example were 9 Buys and 1 Do Not Buy at that particular node and if the target value was set to Buy, .9 is the targeted confidence. However if it is desired to target the Do Not Buy outcome by setting the value to Do Not Buy, then any record falling into this leaf of the tree would get a targeted confidence of .1 or 10%. If the Include validation table option was selected when the decision tree model was built, additional information is provided in a manner similar to that for the Include Confidence Factor option described above. • Targeted Value — The value for the binary targeted confidence. Note that Include Confidence Factor and Targeted Confidence are mutually exclusive options, so that only one of the two may be selected. • Create Profiling Tables — If this option is selected, additional tables are created to profile the leaf nodes in the tree and to link scored rows to the leaf nodes that they correspond to. To do this, a node ID field is added to the scored output table and two additional tables are built to describe the leaf nodes. One table contains confidence factor or targeted confidence (if requested) and prediction information (named by appending “_1” to the scored output table name), and the other contains the rules corresponding to each leaf node (named by appending “_2” to the scored output table name). Note however that selection of the option to Create Profiling Tables is ignored if the Evaluate scoring method or the output option to Generate the SQL for this analysis but do not execute it is selected. It is also ignored if the analysis is being refreshed by a Refresh analysis that requests the creation of a stored procedure. 212 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Tree Scoring Tree Scoring - OUTPUT On the Tree Scoring dialog click on OUTPUT: Figure 128: Tree Scoring > Output On this screen select: • Output Table • Database name — The name of the database. • Table name — The name of the scored output table to be created. • Create output table using the FALLBACK keyword — If a table is selected, it will be built with FALLBACK if this option is selected • Create output table using the MULTISET keyword — This option is not enabled for scored output tables; the MULTISET keyword is not used. • Advertise Output — The Advertise Output option “advertises” output (including Profiling Tables if requested) by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate the SQL for this analysis, but do not execute it — If this option is selected the analysis will only generate SQL, returning it and terminating immediately. Note: To create a stored procedure to score this model, use the Refresh analysis. Run the Tree Scoring Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Tree Scoring The results of running the Teradata Warehouse Miner Decision Tree Scoring Analysis include a variety of statistical reports on the scored model. All of these results are outlined below. Teradata Warehouse Miner User Guide - Volume 1 213 Chapter 2: Scoring Tree Scoring Tree Scoring - RESULTS - Reports On the Tree Scoring dialog click RESULTS and then click on reports (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 129: Tree Scoring > Results > Reports • Decision Tree Score Report • Resulting Scored Table Name — This is the name given the table with the scored values of the decision tree model. • Number of Rows in Scored Table — This is the number of rows in the scored decision tree table. • Confusion Matrix — A N x (N+2) (for N outcomes of the dependent variable) confusion matrix is given with the following format: Table 54: Confusion Matrix Actual ‘0’ Actual ‘1’ … Actual ‘N’ Correct Incorrect Predicted ‘0’ # correct ‘0’ Predictions # incorrect‘1’ Predictions … # incorrect ‘N’ Predictions Total Correct ‘0’ Predictions Total Incorrect ‘0’ Predictions Predicted ‘1’ # incorrect‘0’ Predictions # correct ‘1’ Predictions … # incorrect ‘N’ Predictions Total Correct ‘1’ Predictions Total Incorrect ‘1’ Predictions … … … … … … … Predicted ‘N’ # incorrect‘0’ Predictions # incorrect ‘1’ Predictions … # correct ‘N’ Predictions Total Correct ‘N’ Predictions Total Incorrect ‘N’ Predictions • Cumulative Lift Table — The Cumulative Lift Table demonstrates how effective the model is in estimating the dependent variable. It is produced using deciles based on the probability values. Note that the deciles are labeled such that 1 is the highest decile and 10 is the lowest, based on the probability values calculated by logistic regression. The information in this report however is best viewed in the Lift Chart produced as a graph. Note that this is only valid for binary dependent variables. 214 • Decile — The deciles in the report are based on the probability values predicted by the model. Note that 1 is the highest decile and 10 is the lowest. That is, decile 1 contains data on the 10% of the observations with the highest estimated probabilities that the dependent variable is 1. • Count — This column contains the count of observations in the decile. • Response — This column contains the count of observations in the decile where the actual value of the dependent variable is 1. Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Tree Scoring • Pct Response — This column contains the percentage of observations in the decile where the actual value of the dependent variable is 1. • Pct Captured Response — This column contains the percentage of responses in the decile over all the responses in any decile. • Lift — The lift value is the percentage response in the decile (Pct Response) divided by the expected response, where the expected response is the percentage of response or dependent 1-values over all observations. For example, if 10% of the observations overall have a dependent variable with value 1, and 20% of the observations in decile 1 have a dependent variable with value 1, then the lift value within decile 1 is 2.0, meaning that the model gives a “lift” that is better than chance alone by a factor of two in predicting response values of 1 within this decile. • Cumulative Response — This is a cumulative measure of Response, from decile 1 to this decile. • Cumulative Pct Response — This is a cumulative measure of Pct Response, from decile 1 to this decile. • Cumulative Pct Captured Response — This is a cumulative measure of Pct Captured Response, from decile 1 to this decile. • Cumulative Lift — This is a cumulative measure of Lift, from decile 1 to this decile. Tree Scoring - RESULTS - Data On the Tree Scoring dialog click RESULTS and then click on data (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 130: Tree Scoring > Results > Data Results data, if any, is displayed in a data grid as described in the “RESULTS Tab” on page 80 of the Teradata Warehouse Miner User Guide (Volume 1). If a table was created, a sample of rows is displayed here - the size determined by the setting specified by Maximum result rows to display in Tools-Preferences-Limits. The following table is built in the requested Output Database by the Decision Tree Scoring analysis. Note that the options selected affect the structure of the table. Those columns in bold below will comprise the Primary Index. Also note that there may be repeated groups of columns, and that some columns will be generated only if specific options are selected. Teradata Warehouse Miner User Guide - Volume 1 215 Chapter 2: Scoring Tree Scoring Table 55: Output Database table (Built by the Decision Tree Scoring analysis) Name Type Definition Key User Defined One or more key columns, which default to the index, defined in the table to be scored (i.e. in Selected Table). The data type defaults to the same as the scored table, but can be changed via Primary Index Columns. <app_var> User Defined One or more columns as selected under Retain Columns. <dep_var > User Defined The predicted value of the dependent variable. The name used defaults to the Dependent Variable specified when the tree was built. If Use Dependent variable for predicted value column name is not selected, then an appropriate column name must be entered and is used here. The data type used is the same as the Dependent Variable. _tm_node_id FLOAT When the Create profiling tables option is selected this column is included to link each row with a particular leaf node in the decision tree and thereby with a specific set of rules. _tm_target, or FLOAT One of two measures that are mutually exclusive. If the Include Confidence Factor option is selected, _tm_confidence will be generated and populated with Confidence Factors - a measure of how “confident” the model is that it can predict the correct score for a record that falls into a particular leaf node based on the training data the model was built from. (Default) _tm_confidence If the Targeted Confidence (Binary Outcome Only) option is selected, then _tm_ target will be generated and populated with Targeted Confidences for models built with a predicted value that has only 2 outcomes. The Targeted confidence is a measure of how confident the model is that it can predict the correct score for a particular leaf node based upon a user specified Target Value. For example, if a particular decision node had an outcome of 9 “Buys” and 1 “Do Not Buy” at that particular node, setting the Target Value to “Buy”, would generate a .9 or 9% targeted confidence. However if it is desired to set the Target Value to “Do Not Buy”, then any record falling into this leaf of the tree would get a targeted confidence of .1 or 10%. _tm_recalc_target, or FLOAT _tm_recalc_confidence Recalculated versions of the confidence factor or targeted confidence factor based on the original validation table when Score Only is selected, or based on the selected table to score when Evaluate and Score is selected. The following table is built in the requested Output Database by the Decision Tree Scoring analysis when the Create profiling tables option is selected. (It is named by appending “_1” to the scored result table name). Table 56: Output Database table (Built by the Decision Tree Scoring analysis) - Create profiling tables option selected (“_1” appended) Name Type Definition _tm_node_id FLOAT This column identifies a particular leaf node in the decision tree. _tm_target, or FLOAT The confidence factor or targeted confidence factor for this leaf node, as described above for the scored output table. VARCHAR(n) The predicted value of the dependent variable at this leaf node. _tm_confidence _tm_prediction 216 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Tree Scoring The following table is built in the requested Output Database by the Decision Tree Scoring analysis when the Create profiling tables option is selected. (It is named by appending “_2” to the scored result table name). Table 57: Output Database table (Built by the Decision Tree Scoring analysis) - Create profiling tables option selected (“_2” appended) Name Type Definition _tm_node_id FLOAT This column identifies a particular leaf node in the decision tree. _tm_sequence_id FLOAT An integer from 1 to n to order the rules associated with a leaf node. _tm_rule VARCHAR(n) A rule for inclusion in the ruleset for this leaf node in the decision tree (rules are joined with a logical AND). Tree Scoring - RESULTS - Lift Graph On the Tree Scoring dialog click RESULTS and then click on lift graph (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 131: Tree Scoring > Results > Lift Graph This chart displays the information in the Cumulative Lift Table. This is the same graph described in “Results - Logistic Regression” on page 127 as Lift Chart, but applied to possibly new data. Tree Scoring - RESULTS - SQL On the Tree Scoring dialog click RESULTS and then click on SQL (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 132: Tree Scoring > Results > SQL The SQL generated for scoring is returned here, but only if the Score Method was set to Score on the Input - Analysis Parameters tab, and if the Output - Storage option to Generate the SQL for this analysis, but do not execute it was selected. When SQL is displayed here, it may be selected and copied as desired. (Both right-click menu options and buttons to Select All and Copy are available). Teradata Warehouse Miner User Guide - Volume 1 217 Chapter 2: Scoring Tree Scoring Tutorial - Tree Scoring In this example, the same table is scored as was used to build the decision tree model, as a matter of convenience. Typically, this would not be done unless the contents of the table changed since the model was built. Parameterize a Decision Tree Scoring Analysis as follows: • Selected Tables — twm_customer_analysis • Scoring Method — Evaluate and Score • Use the name of the dependent variable as the predicted value column name — Enabled • Targeted Confidence(s) - For binary outcome only — Enabled • Targeted Value — 1 • Result Table Name — twm_score_tree_1 • Primary Index Columns — cust_id Run the analysis, and click on Results when it completes. For this example, the Decision Tree Scoring Analysis generated the following pages. A single click on each page name populates Results with the item. Table 58: Decision Tree Model Scoring Report Resulting Scored Table Name score_tree_1 Number of Rows in Scored File 747 Table 59: Confusion Matrix Actual Non-Response Actual Response Correct Incorrect Predicted 0 340/45.52% 0/0.00% 340/45.52% 0/0.00% Predicted 1 32/4.28% 375/50.20% 375/50.20% 32/4.28% Cumulativ e Lift Table 60: Cumulative Lift Table Captured Response (%) Lift Cumulativ e Response Cumulativ e Response (%) Cumulativ e Captured Response (%) Decile Count Response Response (%) 1 5 5.00 100.00 1.33 1.99 5.00 100.00 1.33 1.99 2 0 0.00 0.00 0.00 0.00 5.00 100.00 1.33 1.99 3 0 0.00 0.00 0.00 0.00 5.00 100.00 1.33 1.99 4 0 0.00 0.00 0.00 0.00 5.00 100.00 1.33 1.99 5 0 0.00 0.00 0.00 0.00 5.00 100.00 1.33 1.99 218 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Factor Scoring Table 60: Cumulative Lift Table Captured Response (%) Lift Cumulativ e Response Cumulativ e Response (%) Cumulativ e Captured Response (%) Decile Count Response Response (%) Cumulativ e Lift 6 402 370.00 92.04 98.67 1.83 375.00 92.14 100.00 1.84 7 0 0.00 0.00 0.00 0.00 375.00 92.14 100.00 1.84 8 0 0.00 0.00 0.00 0.00 375.00 92.14 100.00 1.84 9 0 0.00 0.00 0.00 0.00 375.00 92.14 100.00 1.84 10 340 0.00 0.00 0.00 0.00 375.00 50.20 100.00 1.00 Table 61: Data cust_id cc_acct _tm_target 1362480 1 0.92 1362481 0 0 1362484 1 0.92 1362485 0 0 1362486 1 0.92 … … … Lift Graph Additionally, you can click on Lift Chart to view the contents of the Lift Table graphically. Factor Scoring Factor analysis is designed primarily for the purpose of discovering the underlying structure or meaning in a set of variables and to facilitate their reduction to a fewer number of variables called factors or components. The first goal is facilitated by finding the factor loadings that describe the variables in a data set in terms of a linear combination of factors. The second goal is facilitated by finding a description for the factors as linear combinations of the original variables they describe. These are sometimes called factor measurements or scores. After computing the factor loadings, computing factor scores might seem like an afterthought, but it is somewhat more involved than that. Teradata Warehouse Miner does automate the process however based on the model information stored in metadata results tables, computing factor scores directly in the database by dynamically generating and executing SQL. Teradata Warehouse Miner User Guide - Volume 1 219 Chapter 2: Scoring Factor Scoring Note that Factor Scoring computes factor scores for a data set that has the same columns as those used in performing the selected Factor Analysis. When scoring is performed, a table is created including index (key) columns, optional “retain” columns, and factor scores for each row in the input table being scored. Scoring is performed differently depending on the type of factor analysis that was performed, whether principal components (PCA), principal axis factors (PAF) or maximum likelihood factors (MLF). Further, scoring is affected by whether or not the factor analysis included a rotation. Also, input data is centered based on the mean value of each variable, and if the factor analysis was performed on a correlation matrix, input values are each divided by the standard deviation of the variable in order to normalize to unit length variance. When scoring a table using a PCA factor analysis model, the scores can be calculated directly without estimation, even if an orthogonal rotation was performed. When scoring using a PAF or MLF model, or a PCA model with an oblique rotation, a unique solution does not exist and cannot be directly solved for (a condition known as the indeterminacy of factor measurements). There are many techniques however for estimating factor measurements, and the technique used by Teradata Warehouse Miner is known as estimation by regression. This technique involves regressing each factor on the original variables in the factor analysis model using linear regression techniques. It gives an accurate solution in the “least-squared error” sense but it typically introduces some degree of dependence or correlation in the computed factor scores. A final word about the independence or orthogonality of factor scores is appropriate here. It was pointed out earlier that factor loadings are orthogonal using the techniques offered by Teradata Warehouse Miner unless an oblique rotation is performed. Factor scores however will not necessarily be orthogonal for principal axis factors and maximum likelihood factors and with oblique rotations since scores are estimated by regression. This is a subtle distinction that is an easy source of confusion. That is, the new variables or factor scores created by a factor analysis, expressed as a linear combination of the original variables, are not necessarily independent of each other, even if the factors themselves are. The user may measure their independence however by using the Matrix and Export Matrix function of the product to build a correlation matrix from the factor score table once it is built. Initiate Factor Scoring After generating a Factor Analysis (as described in “Factor Analysis” on page 58) use the following procedure to initiate Factor Scoring: 220 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Factor Scoring 1 Click on the Add New Analysis icon in the toolbar: Figure 133: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Scoring under Categories and then under Analyses double-click on Factor Scoring: Figure 134: Add New Analysis > Scoring > Factor Scoring 3 This will bring up the Factor Scoring dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Factor Scoring - INPUT - Data Selection On the Factor Scoring dialog click on INPUT and then click on data selection: Teradata Warehouse Miner User Guide - Volume 1 221 Chapter 2: Scoring Factor Scoring Figure 135: Factor Scoring > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases — All available source databases that have been added through Connection Properties. • Available Tables — The tables available for scoring are listed in this window, though all may not strictly qualify; the input table to be scored must contain the same column names used in the original analysis. • Available Columns — The columns available for scoring are listed in this window. • Selected Columns • Index Columns — Note that the Selected Columns window is actually a split window for specifying Index and/or Retain columns if desired. If a table is specified as input, the primary index of the table is defaulted here, but can be changed. If a view is specified as input, an index must be provided. • Retain Columns — Other columns within the table being scored can be appended to the scored table, by specifying them here. Columns specified in Index Columns may not be specified here. Select Model Analysis Select from the list an existing Factor Analysis analysis on which to run the scoring. The Factor Analysis analysis must exist in the same project as the Factor Scoring analysis. Factor Scoring - INPUT - Analysis Parameters On the Factor Scoring dialog click on INPUT and then click on analysis parameters: 222 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Factor Scoring Figure 136: Factor Scoring > Input > Analysis Parameters On this screen select: • Scoring Method • Score — Option to create a score table only. • Evaluate — Option to perform model evaluation only. • Evaluate and Score — Option to create a score table and perform model evaluation. • Factor Names — The names of the factor columns in the created table of scores are optional parameters if scoring is selected. The default names of the factor columns are factor1, factor2 ... factorn. Factor Scoring - OUTPUT On the Factor Scoring dialog click on OUTPUT: Figure 137: Factor Scoring > Output On this screen select: • Output Table • Database name — The name of the database. • Table name — The name of the scored output table to be created-required only if a scoring option is selected. • Create output table using the FALLBACK keyword — If a table is selected, it will be built with FALLBACK if this option is selected • Create output table using the MULTISET keyword — This option is not enabled for scored output tables; the MULTISET keyword is not used. • Advertise Output — The Advertise Output option “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Teradata Warehouse Miner User Guide - Volume 1 223 Chapter 2: Scoring Factor Scoring Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate the SQL for this analysis, but do not execute it — If this option is selected the analysis will only generate SQL, returning it and terminating immediately. Note: To create a stored procedure to score this model, use the Refresh analysis. Run the Factor Scoring Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Factor Scoring The results of running the Teradata Warehouse Miner Factor Analysis Scoring/Evaluation Analysis include a variety of statistical reports on the scored model. All of these results are outlined below. Factor Scoring - RESULTS - reports On the Factor Scoring dialog click RESULTS and then click on reports (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 138: Factor Scoring > Results > Reports • Resulting Scored Table — Name of the scored table - equivalent to Result Table Name. • Number of Rows in Scored Table — Number of rows in the Resulting Scored Table. • Evaluation — Model evaluation for factor analysis consists of computing the standard error of estimate for each variable based on working backwards and re-estimating their values using the scored factors. Estimated values of the original data are made using the T factor scoring equation Ŷ = XC where Ŷ is the estimated raw data, X is the scored data, and C is the factor pattern matrix or rotated factor pattern matrix if rotation was included in the model. The standard error of estimate for each variable y in the original data Y is then given by: y – ŷ -------------------------- 2 n–p 224 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Factor Scoring where each ŷ is the estimated value of each variable y, n is the number of observations and p is the number of factors. Factor Scoring - RESULTS - Data On the Factor Scoring dialog click RESULTS and then click on data (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 139: Factor Scoring > Results > Data Results data, if any, is displayed in a data grid as described in “RESULTS Tab” on page 80 of the Teradata Warehouse Miner User Guide (Volume 1). If a table was created, a sample of rows is displayed here - the size determined by the setting specified by Maximum result rows to display in Tools-Preferences-Limits. The following table is built in the requested Output Database by Factor Scoring. Note that the options selected affect the structure of the table. Those columns in bold below will comprise the Unique Primary Index (UPI). Also note that there may be repeated groups of columns, and that some columns will be generated only if specific options are selected. Table 62: Output Database table (Built by Factor Scoring) Name Type Definition Key User Defined One or more unique-key columns which default to the index defined in the table to be scored (i.e. in Selected Tables). The data type defaults to the same as the scored table, but can be changed via Primary Index Columns. <app_var> User Defined One or more columns as selected under Retain Columns. The data type defaults to the same as that within the appended table, but can be changed via Columns Types (for appended columns). Factorx FLOAT A column generated for each scored factor. The names of the factor columns in the created table of scores are optional parameters if scoring is selected. The default names of the factor columns are factor1, factor2, ... factorn, unless Factor Names are specified. (Default) Factor Scoring - RESULTS - SQL On the Factor Scoring dialog click RESULTS and then click on SQL (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Teradata Warehouse Miner User Guide - Volume 1 225 Chapter 2: Scoring Factor Scoring Figure 140: Factor Scoring > Results > SQL The SQL generated for scoring is returned here, but only if the Score Method was set to Score on the Input - Analysis Parameters tab, and if the Output - Storage option to Generate the SQL for this analysis, but do not execute it was selected. When SQL is displayed here, it may be selected and copied as desired. (Both right-click menu options and buttons to Select All and Copy are available). Tutorial - Factor Scoring In this example, the same table is scored as was used to build the factor analysis model. Parameterize a Factor Analysis Scoring Analysis as follows: • Selected Table — twm_customer_analysis • Evaluate and Score — Enabled • Factor Names • Factor1 • Factor2 • Factor3 • Factor4 • Factor5 • Factor6 • Factor7 • Result Table Name — twm_score_factor_1 • Index Columns — cust_id Run the analysis, and click on Results when it completes. For this example, the Factor Analysis Scoring/Evaluation function generated the following pages. A single click on each page name populates Results with the item. Table 63: Factor Analysis Score Report 226 Resulting Scored Table <result_db >.score_factor_1 Number of Rows in Scored Table 747 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Factor Scoring Table 64: Evaluation Variable Name Standard Error of Estimate income 0.4938 age 0.5804 years_with_bank 0.5965 nbr_children 0.6180 female 0.8199 single 0.3013 married 0.3894 separated 0.4687 ccacct 0.6052 ckacct 0.5660 svacct 0.5248 avg_cc_bal 0.4751 avg_ck_bal 0.6613 avg_sv_bal 0.7166 avg_cc_tran_amt 0.8929 avg_cc_tran_cnt 0.5174 avg_ck_tran_amt 0.3563 avg_ck_tran_cnt 0.7187 avg_sv_tran_amt 0.4326 avg_sv_tran_cnt 0.6967 cc_rev 0.3342 Table 65: Data cust_id factor1 factor2 factor3 factor4 factor5 factor6 factor7 1362480 1.43 -0.28 1.15 -0.50 -0.31 -0.05 1.89 1362481 -1.03 -1.37 0.57 -0.08 -0.60 -0.39 -0.55 ... ... ... ... ... ... ... ... Teradata Warehouse Miner User Guide - Volume 1 227 Chapter 2: Scoring Linear Scoring Linear Scoring Once a linear regression model has been built, it can be used to “score” new data, that is, to estimate the value of the dependent variable in the model using data for which its value may not be known. Scoring is performed using the values of the b-coefficients in the linear regression model and the names of the independent variable columns they correspond to. Other information needed includes the table name(s) in which the data resides, the new table to be created, and primary index information for the new table. The result of scoring a linear regression model will be a new table containing primary index columns and an estimate of the dependent variable, optionally including a residual value for each row, calculated as the difference between the estimated value and the actual value of the dependent variable. (The option to include the residual value is available only when model evaluation is requested). Note that Linear Scoring applies a Linear Regression model to a data set that has the same columns as those used in building the model (with the exception that the scoring input table need not include the predicted or dependent variable column unless model evaluation is requested). Linear Regression - Model Evaluation Linear regression model evaluation begins with scoring a table that includes the actual values of the dependent variable. The standard error of estimate for the model is calculated and reported and may be compared to the standard error of estimate reported when the model was built. The standard error of estimate is calculated as the square root of the average squared residual value over all the observations, i.e. y – ŷ -------------------------- 2 n–p–1 where ŷ is the actual value of the dependent variable, is its predicted value, n is the number of observations, and p is the number of independent variables (substituting n-p in the denominator if there is no constant term). Initiate Linear Scoring After generating a Linear Regression analysis (as described in “Linear Regression” on page 86) use the following procedure to initiate Linear Regression Scoring: 228 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Linear Scoring 1 Click on the Add New Analysis icon in the toolbar: Figure 141: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Scoring under Categories and then under Analyses double-click on Linear Scoring: Figure 142: Add New Analysis > Scoring > Linear Scoring 3 This will bring up the Linear Scoring dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Linear Scoring - INPUT - Data Selection On the Linear Scoring dialog click on INPUT and then click on data selection: Teradata Warehouse Miner User Guide - Volume 1 229 Chapter 2: Scoring Linear Scoring Figure 143: Linear Scoring > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases — All available source databases that have been added through Connection Properties. • Available Tables — The tables available for scoring are listed in this window, though all may not strictly qualify; the input table to be scored must contain the same column names used in the original analysis. • Available Columns — The columns available for scoring are listed in this window. • Selected Columns • Index Columns — Note that the Selected Columns window is actually a split window for specifying Index and/or Retain columns if desired. If a table is specified as input, the primary index of the table is defaulted here, but can be changed. If a view is specified as input, an index must be provided. • Retain Columns — Other columns within the table being scored can be appended to the scored table, by specifying them here. Columns specified in Index Columns may not be specified here. Select Model Analysis Select from the list an existing Linear Regression analysis on which to run the scoring. The Linear Regression analysis must exist in the same project as the Linear Scoring analysis. Linear Scoring - INPUT - Analysis Parameters On the Linear Scoring dialog click on INPUT and then click on analysis parameters: 230 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Linear Scoring Figure 144: Linear Scoring > Input > Analysis Parameters On this screen select: • Scoring Method • Score — Option to create a score table only. • Evaluate — Option to perform model evaluation only. • Evaluate and Score — Option to create a score table and perform model evaluation. • Scoring Options • Use Dependent variable for predicted value column name — Option to use the exact same column name as the dependent variable when the model is scored. This is the default option. • • Predicted Value Column Name — If above option is not checked, then enter here the name of the column in the score table which contains the estimated value of the dependent variable. Residual Column Name — If Evaluate and Score is requested, enter the name of the column that will contain the residual values of the evaluation. This column will be populated with the difference between the estimated value and the actual value of the dependent variable. Linear Scoring - OUTPUT On the Linear Scoring dialog click on OUTPUT: Figure 145: Linear Scoring > Output On this screen select: • Output Table • Database name — The name of the database. • Table name — The name of the scored output table to be created-required only if a scoring option is selected. • Create output table using the FALLBACK keyword — If a table is selected, it will be built with FALLBACK if this option is selected Teradata Warehouse Miner User Guide - Volume 1 231 Chapter 2: Scoring Linear Scoring • Create output table using the MULTISET keyword — This option is not enabled for scored output tables; the MULTISET keyword is not used. • Advertise Output — The Advertise Output option “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate the SQL for this analysis, but do not execute it — If this option is selected the analysis will only generate SQL, returning it and terminating immediately.Hint: To create a stored procedure to score this model, use the Refresh analysis. Note: To create a stored procedure to score this model, use the Refresh analysis. Run the Linear Scoring Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Linear Scoring The results of running the Linear Regression Scoring/Evaluation analysis include a variety of statistical reports on the scored model. All of these results are outlined below. Linear Scoring - RESULTS - reports On the Linear Scoring dialog click RESULTS and then click on reports (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 146: Linear Scoring > Results > Reports • Resulting Scored Table — Name of the scored table - equivalent to Result Table Name. • Number of Rows in Scored Table — Number of rows in the Resulting Scored Table. • Evaluation • 232 Minimum Absolute Error Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Linear Scoring • Maximum Absolute Error • Average Absolute Error The term ‘error’ in the evaluation of a linear regression model refers to the difference between the value of the dependent variable predicted by the model and the actual value in a training set of data (data where the value of the dependent variable is known). Considering the absolute value of the error (changing negative differences to positive differences) provides a measure of the magnitude of the error in the model, which is a more useful measure of the model’s accuracy. With this introduction, the terms minimum, maximum and average absolute error have the usual meanings when calculated over all the observations in the input or scored table. • Standard Error of Estimate The standard error of estimate is calculated as the square root of the average squared residual value over all the observations, i.e. y – ŷ -------------------------- 2 n–p–1 where y is the actual value of the dependent variable, ŷ is its predicted value, n is the number of observations, and p is the number of independent variables (substitute n-p in the denominator if there is no constant term). Linear Scoring - RESULTS - data On the Linear Scoring dialog click RESULTS and then click on data (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 147: Linear Scoring > Results > Data Results data, if any, is displayed in a data grid as described in the “RESULTS Tab” on page 80 of the Teradata Warehouse Miner User Guide (Volume 1). If a table was created, a sample of rows is displayed here - the size determined by the setting specified by Maximum result rows to display in Tools-Preferences-Limits. The following table is built in the requested Output Database by Linear Regression scoring. Note that the options selected affect the structure of the table. Those columns in bold below will comprise the Unique Primary Index (UPI). Also note that there may be repeated groups of columns, and that some columns will be generated only if specific options are selected. Teradata Warehouse Miner User Guide - Volume 1 233 Chapter 2: Scoring Linear Scoring Table 66: Output Database table (Built by Linear Regression scoring) Name Type Definition Key User Defined One or more unique-key columns which default to the index defined in the table to be scored (i.e. in Selected Tables). The data type defaults to the same as the scored table, but can be changed via Primary Index Columns. <app_var> User Defined One or more columns as selected under Retain Columns. <dep_var> FLOAT The predicted value of the dependent variable. The name used defaults to the Dependent Variable specified when the model was built. If Use Dependent variable for predicted value column name is not selected, then an appropriate column name must be entered here. FLOAT The residual values of the evaluation, the difference between the estimated value and the actual value of the dependent variable. This is generated only if the Evaluate or Evaluate and Score options are selected. The name defaults to “Residual” unless it is overwritten by the user. (Default) Residual (Default) Linear Scoring - RESULTS - SQL On the Linear Scoring dialog click RESULTS and then click on SQL (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 148: Linear Scoring > Results > SQL The SQL generated for scoring is returned here, but only if the Score Method was set to Score on the Input - Analysis Parameters tab, and if the Output - Storage option to Generate the SQL for this analysis, but do not execute it was selected. When SQL is displayed here, it may be selected and copied as desired. (Both right-click menu options and buttons to Select All and Copy are available). Tutorial - Linear Scoring In this example, the same table is scored as was used to build the linear model, as a matter of convenience. Typically, this would not be done unless the contents of the table changed since the model was built. In the case of this example, the Standard Error of Estimate can be seen to be exactly the same, 10.445, that it was when the model was built (see “Tutorial - Linear Regression” on page 107). Parameterize a Linear Regression Scoring Analysis as follows: • Selected Table — twm_customer_analysis • Evaluate and Score — Enabled • Use dependent variable for predicted value column name — Enabled 234 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Linear Scoring • Residual column name — Residual • Result Table Name — twm_score_linear_1 • Index Columns — cust_id Run the analysis, and click on Results when it completes. For this example, the Linear Regression Scoring/Evaluation Analysis generated the following pages. A single click on each page name populates Results with the item. Table 67: Linear Regression Reports Resulting Scored Table <result_db>.score_linear_1 Number of Rows in Scored Table 747 Table 68: Evaluation Minimum Absolute Error 0.0056 Maximum Absolute Error 65.7775 Average Absolute Error 7.2201 Standard Error of Estimate 10.4451 Table 69: Data cust_id cc_rev Residual 1362480 59.188 15.812 1362481 3.412 -3.412 1362484 12.254 -.254 1362485 28.272 1.728 1362486 -9.026E-02 9.026E-02 1362487 14.325 -1.325 1362488 -5.105 5.105 1362489 69.738 12.262 1362492 53.368 .632 1362496 -5.876 5.876 … … … … … … … … … Teradata Warehouse Miner User Guide - Volume 1 235 Chapter 2: Scoring Logistic Scoring Logistic Scoring Once a logistic regression model has been built, it can be used to “score” new data, that is, to estimate the value of the dependent variable in the model using data for which its value may not be known. Scoring is performed using the values of the b-coefficients in the logistic regression model and the names of the independent variable column names they correspond to. This information resides in the results metadata stored in the Teradata database by Teradata Warehouse Miner. Other information needed includes the table name in which the data resides, the new table to be created, and primary index information for the new table. Scoring a logistic regression model requires some steps beyond those required in scoring a linear regression model. The result of scoring a logistic regression model will be a new table containing primary index columns, the probability that the dependent variable is 1 (representing the response value) rather than 0 (representing the non-response value), and/or an estimate of the dependent variable, either 0 or 1, based on a user specified threshold value. For example, if the threshold value is 0.5, then a value of 1 is estimated if the probability value is greater than or equal to 0.5. The probability is based on the logistic regression functions given earlier. The user can achieve different results based on the threshold value applied to the probability. The model evaluation tables described below can be used to determine what this threshold value should be. Note that Logistic Scoring applies a Logistic Regression model to a data set that has the same columns as those used in building the model (with the exception that the scoring input table need not include the predicted or dependent variable column unless model evaluation is requested). Logistic Regression Model Evaluation The same model evaluation that is available when building a Logistic Regression model is also available when scoring it, including the following report tables. Prediction success table The prediction success table is computed using only probabilities and not estimates based on a threshold value. Using an input table that contains known values for the dependent variable, the sum of the probability values x and 1 – x , which correspond to the probability that the predicted value is 1 or 0 respectively, are calculated separately for rows with actual values of 1 and 0. This produces a report table such as that shown below. Table 70: Prediction Success Table Estimate Response Estimate Non-Response Actual Total Actual Response 306.5325 68.4675 375.0000 Actual Non-Response 69.0115 302.9885 372.0000 Estimated Total 375.5440 371.4560 747.0000 236 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Logistic Scoring An interesting and useful feature of this table is that it is independent of the threshold value that is used in scoring to determine which probabilities correspond to an estimate of 1 and 0 respectively. This is possible because the entries in the “Estimate Response” column are the sums of the probabilities x that the outcome is 1, summed separately over the rows where the actual outcome is 1 and 0 and then totaled. Similarly, the entries in the “Estimate NonResponse” column are the sums of the probabilities 1 – x that the outcome is 0. Multi-threshold Success Table This table provides values similar to those in the prediction success table, but instead of summing probabilities, the estimated values based on a threshold value are summed instead. Rather than just one threshold however, several thresholds ranging from a user specified low to high value are displayed in user specified increments. This allows the user to compare several success scenarios using different threshold values, to aid in the choice of an ideal threshold. It might be supposed that the ideal threshold value would be the one that maximizes the number of correctly classified observations. However, subjective business considerations may be applied by looking at all of the success values. It may be that wrong predictions in one direction (say estimate 1 when the actual value is 0) may be more tolerable than in the other direction (estimate 0 when the actual value is 1). One may, for example, mind less overlooking fraudulent behavior than wrongly accusing someone of fraud. The following is an example of a logistic regression multi-threshold success table. Table 71: Logistic Regression Multi-Threshold Success table Threshold Probability Actual Response, Estimate Response Actual Response, Estimate NonResponse Actual Non-Response, Estimate Response Actual Non-Response, Estimate NonResponse 0.0000 375 0 372 0 0.0500 375 0 326 46 0.1000 374 1 231 141 0.1500 372 3 145 227 0.2000 367 8 93 279 0.2500 358 17 59 313 0.3000 354 21 46 326 0.3500 347 28 38 334 0.4000 338 37 32 340 0.4500 326 49 27 345 0.5000 318 57 27 345 0.5500 304 71 26 346 0.6000 296 79 24 348 Teradata Warehouse Miner User Guide - Volume 1 237 Chapter 2: Scoring Logistic Scoring Table 71: Logistic Regression Multi-Threshold Success table Threshold Probability Actual Response, Estimate Response Actual Response, Estimate NonResponse Actual Non-Response, Estimate Response Actual Non-Response, Estimate NonResponse 0.6500 287 88 22 350 0.7000 279 96 21 351 0.7500 270 105 19 353 0.8000 258 117 18 354 0.8500 245 130 16 356 0.9000 222 153 12 360 0.9500 187 188 10 362 Cumulative Lift table The Cumulative Lift Table is produced for deciles based on the probability values. Note that the deciles are labeled such that 1 is the highest decile and 10 is the lowest, based on the probability values calculated by logistic regression. Within each decile, the following measures are given: 1 count of “response” values 2 count of observations 3 percentage response (percentage of response values within the decile) 4 captured response (percentage of responses over all response values) 5 lift value (percentage response / expected response, where the expected response is the percentage of responses over all observations) 6 cumulative versions of each of the measures above The following is an example of a logistic regression Cumulative Lift Table. Table 72: Logistic Regression Cumulative Lift Table Cumulative Response Cumulative Response (%) Cumulative Captured Response (%) Cumulative Lift Decile Count Response Response (%) Captured Response (%) 1 74.0000 73.0000 98.6486 19.4667 1.9651 73.0000 98.6486 19.4667 1.9651 2 75.0000 69.0000 92.0000 18.4000 1.8326 142.0000 95.3020 37.8667 1.8984 3 75.0000 71.0000 94.6667 18.9333 1.8858 213.0000 95.0893 56.8000 1.8942 4 74.0000 65.0000 87.8378 17.3333 1.7497 278.0000 93.2886 74.1333 1.8583 5 75.0000 63.0000 84.0000 16.8000 1.6733 341.0000 91.4209 90.9333 1.8211 6 75.0000 23.0000 30.6667 6.1333 0.6109 364.0000 81.2500 97.0667 1.6185 238 Lift Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Logistic Scoring Table 72: Logistic Regression Cumulative Lift Table Cumulative Response Cumulative Response (%) Cumulative Captured Response (%) Cumulative Lift Decile Count Response Response (%) Captured Response (%) 7 74.0000 8.0000 10.8108 2.1333 0.2154 372.0000 71.2644 99.2000 1.4196 8 75.0000 2.0000 2.6667 0.5333 0.0531 374.0000 62.6466 99.7333 1.2479 9 75.0000 1.0000 1.3333 0.2667 0.0266 375.0000 55.8036 100.0000 1.1116 10 75.0000 0.0000 0.0000 0.0000 0.0000 375.0000 50.2008 100.0000 1.0000 Lift Initiate Logistic Scoring After generating a Logistic Regression analysis (as described in “Logistic Regression” on page 114) use the following procedure to initiate Logistic Scoring: 1 Click on the Add New Analysis icon in the toolbar: Figure 149: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Scoring under Categories and then under Analyses double-click on Logistic Scoring: Teradata Warehouse Miner User Guide - Volume 1 239 Chapter 2: Scoring Logistic Scoring Figure 150: Add New Analysis > Scoring > Logistic Scoring 3 This will bring up the Logistic Scoring dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Logistic Scoring - INPUT - Data Selection On the Logistic Scoring dialog click on INPUT and then click on data selection: Figure 151: Logistic Scoring > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 240 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Logistic Scoring 2 3 Select Columns From a Single Table • Available Databases — All available source databases that have been added through Connection Properties. • Available Tables — The tables available for scoring are listed in this window, though all may not strictly qualify; the input table to be scored must contain the same column names used in the original analysis. • Available Columns — The columns available for scoring are listed in this window. • Selected Columns • Index Columns — Note that the Selected Columns window is actually a split window for specifying Index and/or Retain columns if desired. If a table is specified as input, the primary index of the table is defaulted here, but can be changed. If a view is specified as input, an index must be provided. • Retain Columns — Other columns within the table being scored can be appended to the scored table, by specifying them here. Columns specified in Index Columns may not be specified here. Select Model Analysis Select from the list an existing Logistic Regression analysis on which to run the scoring. The Logistic Regression analysis must exist in the same project as the Logistic Scoring analysis. Logistic Scoring - INPUT - Analysis Parameters On the Logistic Scoring dialog click on INPUT and then click on analysis parameters: Figure 152: Logistic Scoring > Input > Analysis Parameters On this screen select: • Scoring Method • Score — Option to create a score table only. • Evaluate — Option to perform model evaluation only. • Evaluate and Score — Option to create a score table and perform model evaluation. • Scoring Options • Include Probability Score Column — Inclusion of a column in the score table that contains the probability between 0 and 1 that the value of the dependent variable is 1 is an optional parameter when scoring is selected. The default is to include a probability score column in the created score table. (Either the probability score or the estimated value or both must be requested when scoring). • Column Name — Column name containing the probability between 0 and 1 that the Teradata Warehouse Miner User Guide - Volume 1 241 Chapter 2: Scoring Logistic Scoring value of the dependent variable is 1. • Include Estimate from Threshold Column — Inclusion of a column in the score table that contains the estimated value of the dependent variable is an option when scoring is selected. The default is to include an estimated value column in the created score table. (Either the probability score or the estimated value or both must be requested when scoring). • Column Name — Column name containing the estimated value of the dependent variable. • Threshold Default — The threshold value is a value between 0 and 1 that determines which probabilities result in an estimated value of 0 or 1. For example, with a threshold value of 0.3, probabilities of 0.3 or greater yield an estimated value of 1, while probabilities less than 0.3 yield an estimated value of 0. The threshold option is valid only if the Include Estimate option has been requested and scoring is selected. If the Include Estimate option is requested but the threshold value is not specified, a default threshold value of 0.5 is used. • Evaluation Options • Prediction Success Table — Creates a prediction success table using sums of probabilities rather than estimates based on a threshold value. The default value is to include the Prediction Success Table. (This only applies if evaluation is requested). • Multi-Threshold Success Table — This table provides values similar to those in the prediction success table, but based on a range of threshold values, thus allowing the user to compare success scenarios using different threshold values. The default value is to include the multi-threshold success table. (This only applies if evaluation is requested). • Threshold Begin • Threshold End • Threshold Increment Specifies the threshold values to be used in the multi-threshold success table. If the computed probability is greater than or equal to a threshold value, that observation is assigned a 1 rather than a 0. Default values are 0, 1 and .05 respectively. • Cumulative Lift Table — Produce a cumulative lift table for deciles based on probability values. The default value is to include the cumulative lift table. (This only applies if evaluation is requested). Logistic Scoring - OUTPUT On the Logistic Scoring dialog click on OUTPUT: Figure 153: Logistic Scoring > Output 242 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Logistic Scoring On this screen select: • Output Table • Database name — The name of the database. • Table name — The name of the scored output table to be created-required only if a scoring option is selected. • Create output table using the FALLBACK keyword — If a table is selected, it will be built with FALLBACK if this option is selected. • Create output table using the MULTISET keyword — This option is not enabled for scored output tables; the MULTISET keyword is not used. • Advertise Output — The Advertise Output option “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate the SQL for this analysis, but do not execute it — If this option is selected the analysis will only generate SQL, returning it and terminating immediately. Note: To create a stored procedure to score this model, use the Refresh analysis. Run the Logistic Scoring Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Logistic Scoring The results of running the Logistic Scoring analysis include a variety of statistical reports on the scored model, and if selected, a Lift Chart. All of these results are outlined below. It is important to note that although a response value other than 1 may have been indicated when the Logistic Regression model was built, the Logistic Regression Scoring analysis will always use the value 1 as the response value, and the value 0 for the non-response value(s). Logistic Scoring - RESULTS - Reports On the Logistic Scoring dialog click RESULTS and then click on reports (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Teradata Warehouse Miner User Guide - Volume 1 243 Chapter 2: Scoring Logistic Scoring Figure 154: Logistic Scoring > Results > Reports • Resulting Scored Table — Name of the scored table - equivalent to Result Table Name. • Number of Rows in Scored Table — Number of rows in the Resulting Scored Table. • Prediction Success Table — This is the same report described in “Results - Logistic Regression” on page 127, but applied to possibly new data. • Multi-Threshold Success Table — This is the same report described in “Results - Logistic Regression” on page 127, but applied to possibly new data. • Cumulative Lift Table — This is the same report described in “Results - Logistic Regression” on page 127, but applied to possibly new data. Logistic Scoring - RESULTS - Data On the Logistic Scoring dialog click RESULTS and then click on data (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 155: Logistic Scoring > Results > Data Results data, if any, is displayed in a data grid as described in “RESULTS Tab” on page 80 of the Teradata Warehouse Miner User Guide (Volume 1). If a table was created, a sample of rows is displayed here - the size determined by the setting specified by Maximum result rows to display in Tools-Preferences-Limits. The following table is built in the requested Output Database by Logistic Regression scoring. Note that the options selected affect the structure of the table. Those columns in bold below will comprise the Unique Primary Index (UPI). Also note that there may be repeated groups of columns, and that some columns will be generated only if specific options are selected. Table 73: Output Database table (Built by Logistic Regression scoring) Name Type Definition Key User Defined One or more unique-key columns which default to the index defined in the table to be scored (i.e. in Selected Table). The data type defaults to the same as the scored table, but can be changed via Primary Index Columns. <app_var> User Defined One or more columns as selected under Retain Columns. 244 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Logistic Scoring Table 73: Output Database table (Built by Logistic Regression scoring) Name Type Definition Probability FLOAT A probability between 0 and 1 that the value of the dependent variable is 1. The name used defaults to “Probability” unless an appropriate column name is entered. Generated only if Include Probability Score Column is selected. The default is to not include a probability score column in the created score table. (Either the probability score or the estimated value or both must be requested when scoring). FLOAT The estimated value of the dependent variable,. The default is to not include an estimated value column in the created score table. Generated only if Include Estimate from Threshold Column is selected. (Either the probability score or the estimated value or both must be requested when scoring). (Default) Estimate (Default) Logistic Scoring - RESULTS - Lift Graph On the Logistic Scoring dialog click RESULTS and then click on lift graph (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 156: Logistic Scoring > Results > Lift Graph This chart displays the information in the Cumulative Lift Table. This is the same graph described in “Results - Logistic Regression” on page 127 as Lift Chart, but applied to possibly new data. Logistic Scoring - RESULTS - SQL On the Logistic Scoring dialog click RESULTS and then click on SQL (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 157: Logistic Scoring > Results > SQL The SQL generated for scoring is returned here, but only if the Score Method was set to Score on the Input - Analysis Parameters tab, and if the Output - Storage option to Generate the SQL for this analysis, but do not execute it was selected. When SQL is displayed here, it may be selected and copied as desired. (Both right-click menu options and buttons to Select All and Copy are available). Teradata Warehouse Miner User Guide - Volume 1 245 Chapter 2: Scoring Logistic Scoring Tutorial - Logistic Scoring In this example, the same table is scored as was used to build the logistic regression model, as a matter of convenience. Typically, this would not be done unless the contents of the table changed since the model was built. Parameterize a Logistic Regression Scoring Analysis as follows: • Selected Table — twm_customer_analysis • Evaluate and Score — Enabled • Include Probability Score Column — Enabled • Column Name — Probability • Include Estimate from Threshold Column — Enabled • Column Name — Estimate • Threshold Default — 0.35 • Prediction Success Table — Enabled • Multi-Threshold Success Table — Enabled • Threshold Begin — 0 • Threshold End — 1 • Threshold Increment — 0.05 • Cumulative Lift Table — Enabled • Result Table Name — score_logistic_1 • Index Columns — cust_id Run the analysis, and click on Results when it completes. For this example, the Logistic Regression Scoring/Evaluation Analysis generated the following pages. A single click on each page name populates Results with the item. Table 74: Logistic Regression Model Scoring Report Resulting Scored Table <result_db>.score_logistic_1 Number of Rows in Scored Table 747 Table 75: Prediction Success Table Estimate Response Estimate Non-Response Actual Total Actual Response 304.58 / 40.77% 70.42 / 9.43% 375.00 / 50.20% Actual Non-Response 70.41 / 9.43% 301.59 / 40.37% 372.00 / 49.80% Estimated Total 374.99 / 50.20% 372.01 / 49.80% 747.00 / 100.00% 246 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Logistic Scoring Table 76: Multi-Threshold Success Table Threshold Probability Actual Response, Estimate Response Actual Response, Estimate NonResponse Actual Non-Response, Estimate Response Actual Non-Response, Estimate NonResponse 0.0000 375 0 372 0 0.0500 375 0 353 19 0.1000 374 1 251 121 0.1500 373 2 152 220 0.2000 369 6 90 282 0.2500 361 14 58 314 0.3000 351 24 37 335 0.3500 344 31 29 343 0.4000 329 46 29 343 0.4500 318 57 28 344 0.5000 313 62 24 348 0.5500 305 70 23 349 0.6000 291 84 23 349 0.6500 286 89 21 351 0.7000 276 99 20 352 0.7500 265 110 20 352 0.8000 253 122 20 352 0.8500 243 132 16 356 0.9000 229 146 13 359 0.9500 191 184 11 361 Lift Table 77: Cumulative Lift Table Cumulative Response Cumulative Response (%) Cumulative Captured Response (%) Cumulative Lift Decile Count Response Response (%) Captured Response (%) 1 74.0000 73.0000 98.6486 19.4667 1.9651 73.0000 98.6486 19.4667 1.9651 2 75.0000 69.0000 92.0000 18.4000 1.8326 142.0000 95.3020 37.8667 1.8984 3 75.0000 71.0000 94.6667 18.9333 1.8858 213.0000 95.0893 56.8000 1.8942 Teradata Warehouse Miner User Guide - Volume 1 247 Chapter 2: Scoring Logistic Scoring Table 77: Cumulative Lift Table Cumulative Response Cumulative Response (%) Cumulative Captured Response (%) Cumulative Lift Decile Count Response Response (%) Captured Response (%) 4 74.0000 65.0000 87.8378 17.3333 1.7497 278.0000 93.2886 74.1333 1.8583 5 75.0000 66.0000 88.0000 17.6000 1.7530 344.0000 92.2252 91.7333 1.8371 6 75.0000 24.0000 32.0000 6.4000 0.6374 368.0000 82.1429 98.1333 1.6363 7 74.0000 4.0000 5.4054 1.0667 0.1077 372.0000 71.2644 99.2000 1.4196 8 73.0000 2.0000 2.7397 0.5333 0.0546 374.0000 62.8571 99.7333 1.2521 9 69.0000 1.0000 1.4493 0.2667 0.0289 375.0000 56.4759 100.0000 1.1250 10 83.0000 0.0000 0.0000 0.0000 0.0000 375.0000 50.2008 100.0000 1.0000 Lift Table 78: Data cust_id Probability Estimate 1362480 1.00 1 1362481 0.08 0 1362484 1.00 1 1362485 0.14 0 1362486 0.66 1 1362487 0.86 1 1362488 0.07 0 1362489 1.00 1 1362492 0.29 0 1362496 0.35 1 … ... ... Lift Graph By default, the Lift Graph displays the cumulative measure of the percentage of observations in the decile where the actual value of the dependent variable is 1, from decile 1 to this decile (Cumulative, %Response). 248 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Neural Networks Scoring Figure 158: Logistic Scoring Tutorial: Lift Graph Neural Networks Scoring Neural Networks Scoring is implemented by saving each of the retained models from a Neural Networks Analysis in PMML. After the user selects a particular model to score, the scoring is the same as PMML scoring. (Refer to “PMML Scoring” on page 295 of the Teradata Warehouse Miner User Guide (Volume 2)). Initiate Neural Networks Scoring Use the following procedure to initiate a Neural Networks Scoring analysis: 1 Click on the Add New Analysis icon in the toolbar: Figure 159: Add New Analysis from toolbar Teradata Warehouse Miner User Guide - Volume 1 249 Chapter 2: Scoring Neural Networks Scoring 2 In the resulting Add New Analysis dialog box, click on Scoring under Categories and then under Analyses double-click on Neural Net Scoring: Figure 160: Add New Analysis > Scoring > Neural Net Scoring 3 This will bring up the Neural Networks Scoring dialog in which you will enter INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Neural Networks Scoring - INPUT - Data Selection On the Neural Networks Scoring dialog click on INPUT and then click on data selection: 250 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Neural Networks Scoring Figure 161: Neural Networks Scoring > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. (Note that since this analysis cannot select from a volatile input table, Available Analyses will contain only those qualifying analyses that create an output table or view). For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 Select Columns From a Single Table • Available Databases — All available source databases that have been added through Connection Properties. • Available Tables — The tables available for scoring are listed in this window, though all may not strictly qualify; the input table to be scored must contain the same column names used in the original analysis. • Available Columns — The columns available for scoring are listed in this window. Teradata Warehouse Miner User Guide - Volume 1 251 Chapter 2: Scoring Neural Networks Scoring • 3 Selected Columns • Index Columns — Note that the Selected Columns window is actually a split window for specifying Index and/or Retain columns if desired. If a table is specified as input, the primary index of the table is defaulted here, but can be changed. If a view is specified as input, an index must be provided. • Retain Columns — Other columns within the table being scored can be appended to the scored table, by specifying them here. Columns specified in Index Columns may not be specified here. Select Model Analysis Select from the list an existing Neural Networks analysis on which to run the scoring. The Neural Networks analysis must exist in the same project as the Neural Networks Scoring analysis. 4 Select Model Choose a particular Neural Network model from the above analysis to be used for scoring. (Note that when a saved analysis with a valid model is first loaded into the project space its models are embedded in the analysis and the displayed models reflect the analysis the model was originally built from, even if it resided on another client machine). Neural Networks Scoring - OUTPUT On the Neural Networks Scoring dialog click on OUTPUT and then storage: Figure 162: Neural Networks Scoring > Output On this screen select: • Output Table 252 • Database name — The name of the database. • Table name — The name of the scored output table to be created. • Create output table using the FALLBACK keyword — If a table is selected, it will be built with FALLBACK if this option is selected • Create output table using the MULTISET keyword — This option is not enabled for scored output tables; the MULTISET keyword is not used. • Advertise Output — The Advertise Output option “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Neural Networks Scoring • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate the SQL for this analysis, but do not execute it — If this option is checked the SQL to score this model will be generated but not executed. • Maximum SQL statement size allowed (default 64000) — The SQL statements generated will not exceed this maximum value in characters. • Generate as a stored procedure with name — (This option is no longer available. To create a stored procedure to score this model, use the Refresh analysis and select this analysis as the analysis to be refreshed). Note: To create a stored procedure to score this model, use the Refresh analysis. Run the Neural Networks Scoring Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Neural Networks Scoring The results of running the Teradata Warehouse Miner Neural Networks Scoring Analysis include the following outlined below. NEURAL NETWORKS Scoring - RESULTS - Reports On the NEURAL NETWORKS Scoring dialog click RESULTS and then click on reports (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 163: Neural Networks Scoring > Results > Reports • NEURALNET Score Report • Resulting Scored Table Name — This is the name given the table with the scored values of the model. • Number of Rows in Scored Table — This is the number of rows in the scored table. Teradata Warehouse Miner User Guide - Volume 1 253 Chapter 2: Scoring Neural Networks Scoring NEURAL NETWORKS Scoring - RESULTS - Data On the NEURAL NETWORKS Scoring dialog click RESULTS and then click on data (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): Figure 164: Neural Networks Scoring > Results > Data Results data, if any, is displayed in a data grid as described in “RESULTS Tab” on page 80 of the Teradata Warehouse Miner User Guide (Volume 1). After clicking the “Load” button, a sample of rows from the scored table will be displayed here - the size determined by the setting specified by Maximum result rows to display in ToolsPreferences-Limits. By default, the index of the table being scored as well as the dependent column prediction are in the scored table - additional columns as specified in the OUTPUT panel may be displayed as well. The following table is built in the requested Output Database by the NEURAL NETWORKS Scoring analysis. Note that the options selected affect the structure of the table. Those columns in bold below will comprise the Primary Index. Also note that there may be repeated groups of columns, and that some columns will be generated only if specific options are selected. Table 79: Output Database table (Built by Neural Networks scoring) Name Type Definition <app_var> User Defined One or more columns as selected under Retain Columns. <dep_var > User Defined The predicted value of the dependent variable. The name used defaults to the neuron number. The data type used is the same as the Dependent Variable. FLOAT If any additional probability output is requested on the OUTPUT panel, it will be displayed using the name provided in the PMML model. (Default) P_<dep_var><value> NEURAL NETWORKS Scoring - RESULTS - SQL On the NEURAL NETWORKS Scoring dialog click RESULTS and then click on SQL (note that the RESULTS tab will be grayed-out/disabled until after the analysis is completed): 254 Teradata Warehouse Miner User Guide - Volume 1 Chapter 2: Scoring Neural Networks Scoring Figure 165: Neural Networks Scoring > Results > SQL The SQL generated for scoring is returned here, but only if the Output - Storage option to Generate the SQL for this analysis, but do not execute it was selected. When SQL is displayed here, it may be selected and copied as desired. (Both right-click menu options and buttons to Select All and Copy are available). Neural Networks Scoring Tutorial 1 Create a new Neural Networks analysis to score named Neural Networks2 equivalent to Neural Networks Tutorial 2: Performing Classification with Fictitious Banking Data. 2 Create a new Neural Net Scoring analysis named Neural Net Scoring2. Parameterize this Neural Net Scoring analysis as follows: • Available Tables — twm_customer_analysis • Select Model Analysis — Neural Networks2 • Selected Model — (choose one of the models from the pull-down window) • Index Columns — cust_id Parameterize the output as follows: • Result Table Name — twm_score_neural_net2 Run the analysis, and click on Results when it completes. For this example, the Neural Scoring Analysis generated the following results. Teradata Warehouse Miner User Guide - Volume 1 255 Chapter 2: Scoring Neural Networks Scoring Figure 166: Neural Networks Scoring Tutorial: Report The predicted value of the dependent variable, ccacct, is displayed for each cust_id, as shown below (after sorting). Note that results may vary depending on the random element in the construction of neural network models. Figure 167: Neural Networks Scoring Tutorial: Data (Note that the scoring SQL could only be displayed if the Output option to Generate the SQL for this analysis, but do not execute it were selected, which was not the case in this example). 256 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Overview CHAPTER 3 Statistical Tests What’s In This Chapter For more information, see these subtopics: 1 “Overview” on page 257 2 “Parametric Tests” on page 261 3 “Binomial Tests” on page 286 4 “Kolmogorov-Smirnov Tests” on page 299 5 “Tests Based on Contingency Tables” on page 329 6 “Rank Tests” on page 342 Overview Teradata Warehouse Miner contains both parametric and nonparametric statistical tests from the classical statistics literature, as well as more recently developed tests. In addition, “group by” variables permit the ability to statistically analyze data groups defined by selected variables having specific values. In this way, multiple tests can be conducted at once to provide a profile of customer data showing hidden clues about customer behavior. In simplified terms, what statistical inference allows us to do is to find out whether the outcome of an experiment could have happened by accident, or if it is extremely unlikely to have happened by chance. Of course a very well designed experiment would have outcomes which are clearly different, and require no statistical test. Unfortunately, in nature noisy outcomes of experiments are common, and statistical inference is required to get the answer. It doesn’t matter whether our data come from an experiment we designed, or from a retail database. Questions can be asked of the data, and statistical inference can provide the answer. What is statistical inference? It is a process of drawing conclusions about parameters of a statistical distribution. In summary, there are three principal approaches to statistical inference. One type of statistical inference is Bayesian estimation, where conclusions are based upon posterior judgments about the parameter given an experimental outcome. A second type is based on the likelihood approach, in which all conclusions are inferred from the likelihood function of the parameter given an experimental outcome. A third type of inference is hypothesis testing, which includes both nonparametric and parametric inference. For nonparametric inference, estimators concerning the distribution function are independent of the specific mathematical form of the distribution function. Parametric inference, by contrast, involves estimators about the distribution function that assumes a particular mathematical form, most often the normal distribution. Parametric tests are based on the Teradata Warehouse Miner User Guide - Volume 1 257 Chapter 3: Statistical Tests Overview sampling distribution of a particular statistic. Given knowledge of the underlying distribution of a variable, how the statistic is distributed in multiple equal-size samples can be predicted. The statistical tests provided in Teradata Warehouse Miner are solely those of the hypothesis testing type, both parametric and nonparametric. Hypothesis tests generally belong to one of five classes: 1 parametric tests including the class of t-tests and F-tests assuming normality of data populations 2 nonparametric tests of the binomial type 3 nonparametric tests of the chi square type, based on contingency tables. 4 nonparametric tests based on ranks 5 nonparametric tests of the Kolmogorov-Smirnov type Within each class of tests there exist many variants, some of which have risen to the level of being named for their authors. Often tests have multiple names due to different originators. The tests may be applied to data in different ways, such as on one sample, two samples or multiple samples. The specific hypothesis of the test may be two-tailed, upper-tailed or lowertailed. Hypothesis tests vary depending on the assumptions made in the context of the experiment, and care must be exercised that they are valid in the particular context of the data to be examined. For example, is it a fair assumption that the variables are normally distributed? The choice of which test to apply will depend on the answer to this question. Failure to exercise proper judgement in which test to apply may result in false alarms, where the null hypothesis is rejected incorrectly, or misses, where the null hypothesis is accepted improperly. Note: Identity columns, i.e. columns defined with the attribute “GENERATED … AS IDENTITY”, cannot be analyzed by many of the statistical test functions and should therefore generally be avoided. Summary of Tests Parametric Tests Tests include the T-test, the F(1-way), F(2-way with equal Sample Size), F(3-way with equal Sample Size), and the F(2-way with unequal Sample Size). The two-sample t-test checks if two population means are equal. The ANOVA or F test determines if significant differences exist among treatment means or interactions. It’s a preliminary test that indicates if further analysis of the relationship among treatment means is warranted. Tests of the Binomial Type These tests include the Binomial test and Sign test. The data for a binomial test is assumed to come from n independent trials, and have outcomes in either of two classes. The binomial test reports whether the probability that the outcome is of the first class is a particular p_value, p*, usually ½. 258 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Overview Tests Based on Contingency Tables - Chi Square Type Tests include the Chi Square and Median test. The Chi Square Test determines whether the probabilities observed from data in a RxC contingency table are the same or different. Additional statistics provided are Phi coefficient, Cramer’s V, Likelihood Ratio Chi Square, Continuity-Adjusted Chi-Square, and Contingency Coefficient The Median test is a special case of the chi-square test with fixed marginal totals, testing whether several samples came from populations with the same median. Tests of the Kolmogorov-Smirnov Type These tests include the Kolmogorov-Smirnov and Lilliefors tests for goodness of fit to a particular distribution (normal), the Shapiro-Wilk and D'Agostino-Pearson tests of normality, and the Smirnov test of equality of two distributions. Tests Based on Ranks Tests include the MannWhitney test for 2 independent samples, Kruskal-Wallis test for k independent samples, Wilcoxon Signed Ranks test, and Friedman test. The Friedman test is an extension of the sign test for several independent samples. It is a test for treatment differences in a randomized, complete block design. Additional statistics provided are Kendall’s Coefficient of Concordance (W) and Spearman’s Rho. Data Requirements The following chart summarizes how the Statistical Test functions handle various types of input. Those cases with the note “should be normal numeric” will give warnings for any type of input that is not standard numeric, i.e. for character data, dates, big integers or decimals, etc. (In the table below, cat is an abbreviation for categorical, num for numeric and bignum for big integers or decimals). Table 80: Statistical Test functions handling of input Test Input Columns Tests Return Results With Note Median column of interest cat, num, date, bignum can be anything Median columns cat, num, date, bignum can be anything Median group by columns cat, num, date, bignum can be anything Chi Square 1st columns cat, num, date, bignum can be anything (limit of 2000 distinct value pairs) Chi Square 2nd columns cat, num, date, bignum can be anything Mann Whitney column of interest cat, num, date, bignum can be anything Teradata Warehouse Miner User Guide - Volume 1 259 Chapter 3: Statistical Tests Overview Table 80: Statistical Test functions handling of input Test Input Columns Tests Return Results With Note Mann Whitney columns cat, num, date, bignum can be anything Mann Whitney group by columns cat, num, date, bignum can be anything Wilcoxon 1st column num, date, bignum should be normal numeric Wilcoxon 2nd column num, date, bignum should be normal numeric Wilcoxon group by columns cat, num, date, bignum can be anything Friedman column of interest num should be normal numeric Friedman treatment column special count requirements Friedman block column special count requirements Friedman group by columns cat, num, date, bignum can be anything F(n)way column of interest num should be normal numeric F(n)way columns cat, num, date, bignum can be anything F(n)way group by columns cat, num, date, bignum can be anything F(2)way ucc column of interest num should be normal numeric F(2)way ucc columns cat, num, date, bignum can be anything F(2)way ucc group by columns cat, num, date, bignum can be anything T Paired 1st column num should be normal numeric T Paired 2nd column num, date, bignum should be normal numeric T Paired group by columns cat, num, date, bignum can be anything T Unpaired 1st column num should be normal numeric T Unpaired 2nd column num, date, bignum should be normal numeric T Unpaired group by columns cat, num, date, bignum can be anything T Unpaired w ind 1st column num should be normal numeric T Unpaired w ind indicator column cat, num, date, bignum can be anything 260 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Table 80: Statistical Test functions handling of input Test Input Columns Tests Return Results With Note T Unpaired w ind group by columns cat, num, date, bignum can be anything Kolmogorov-Smirnov column of interest num, date, bignum should be normal numeric Kolmogorov-Smirnov group by columns cat, num, date, bignum can be anything Lilliefors column of interest num, date, bignum should be normal numeric Lilliefors group by columns cat, num, bignum can be anything but date Shapiro-Wilk column of interest num, date, bignum should be normal numeric Shapiro-Wilk group by columns cat, num, date, bignum can be anything D'Agostino-Pearson column of interest num should be normal numeric D'Agostino-Pearson group by columns cat, num, bignum can be anything but date Smirnov column of interest cat, num, date, bignum should be normal numeric Smirnov columns must be 2 distinct values must be 2 distinct values Smirnov group by columns cat, num, bignum can be anything but date Binomial 1st column num, date, bignum should be normal numeric Binomial 2nd column num, date, bignum should be normal numeric Binomial group by columns cat, num, date, bignum can be anything Sign 1st column num, bignum should be normal numeric Sign group by columns cat, num, date, bignum can be anything Parametric Tests Parametric Tests are a class of statistical test which requires particular assumptions about the data. These often include that the observations are independent and normally distributed. A researcher may want to verify the assumption of normality before using a parametric test. He Teradata Warehouse Miner User Guide - Volume 1 261 Chapter 3: Statistical Tests Parametric Tests could use any of the four provided described below, such as the Kolmogorov-Smirnov test for normality, to determine if his use of one of the parametric tests were appropriate. Two Sample T-Test for Equal Means For the paired t test, a one-to-one correspondence must exist between values in both samples. The test is whether paired values have mean differences which are not significantly different from zero. It assumes differences are identically distributed normal random variables, and that they are independent. The unpaired t test is similar, but there is no correspondence between values of the samples. It assumes that within each sample, values are identically distributed normal random variables, and that the two samples are independent of each other. The two sample sizes may be equal or unequal. Variances of both samples may be assumed to be equal (homoscedastic) or unequal (heteroscedastic). In both cases, the null hypothesis is that the population means are equal. Test output is a p-value which compared to the threshold determines whether the null hypothesis should be rejected. Two methods of data selection are available for the unpaired t test: The first, the “T Unpaired” simply selects the columns with the two unpaired datasets, some of which may be NULL. The second, “T Unpaired with Indicator”, selects the column of interest and a second indicator column which determines to which group the first variable belongs. If the indicator variable is negative or zero, it will be assigned to the first group; if it is positive, it will be assigned to the second group. The two sample t test for unpaired data is defined as shown below (though calculated differently in the SQL): Table 81: Two sample t tests for unpaired data H0 : 1 = 2 Ha: 1 2 Test Statistic: Y1 – Y2 T = --------------------------------------------------2 2 s1 N1 + s2 N2 where N1 and N2 are the sample sizes, and s22 are the sample variances. Y 1 and Y 2 are the sample means, and s12 Initiate a Two Sample T-Test Use the following procedure to initiate a new T-Test in Teradata Warehouse Miner: 262 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests 1 Click on the Add New Analysis icon in the toolbar: Figure 168: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Parametric Tests: Figure 169: Add New Analysis > Statistical Tests > Parametric Tests 3 This will bring up the Parametric Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. T-Test - INPUT - Data Selection On the Parametric Tests dialog click on INPUT and then click on data selection: Teradata Warehouse Miner User Guide - Volume 1 263 Chapter 3: Statistical Tests Parametric Tests Figure 170: T-Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the parametric tests available (F(n-way), F(2-way with unequal cell counts, T Paired, T Unpaired, T Unpaired with Indicator). Select “T Paired”, “T Unpaired”, or “T Unpaired with Indicator”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as First Column, Second Column or Group By Columns. Make sure you have the correct portion of the window highlighted. 264 • First Column — The column that specifies the first variable for the Parametric Test analysis. • Second Column (or Indicator Column) — The column that specifies the second variable for the Parametric Test analysis. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests (Or the column that determines to which group the first variable belongs. If negative or zero, it will be assigned to the first group; if it is positive, it will be assigned to the second group). • Group By Columns — The column(s) that specifies the variable(s) whose distinct value combinations will categorize the data, so a separate test is performed on each category. T-Test - INPUT - Analysis Parameters On the Parametric Tests dialog click on INPUT and then click on analysis parameters: Figure 171: T-Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. • Equal Variance — Check this box if the “equal variance” assumption is to be used. Default is “unequal variance”. T-Test - OUTPUT On the Parametric Tests dialog click on OUTPUT: Figure 172: T-Test > Output On this screen select: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure Teradata Warehouse Miner User Guide - Volume 1 265 Chapter 3: Statistical Tests Parametric Tests here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the T-Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - T-Test Analysis The results of running the T-Test analysis include a table with a row for each group-by variable requested, as well as the SQL to perform the statistical analysis. All of these results are outlined below. T-Test - RESULTS - SQL On the Parametric Tests dialog click on RESULTS and then click on SQL: 266 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Figure 173: T-Test > Results > SQL The series of SQL statements comprise the T-Test analysis. It is always returned, and is the only item returned when the Generate SQL Without Executing option is used. T-Test - RESULTS - Data On the Parametric Tests dialog click on RESULTS and then click on data: Figure 174: T-Test > Results > Data The output table is generated by the T-Test analysis for each group-by variable combination. Output Columns - T-Test Analysis The following table is built in the requested Output Database by the T-Test analysis. Any group-by columns will comprise the Unique Primary Index (UPI). Table 82: Output Database table Name Type Definition D_F INTEGER Degrees of Freedom for the group-by values selected. T Float The computed value of the T statistic TTestPValue Float The probability associated with the T statistic TTestCallP Char The TTest result: a=accept, p=reject (positive), n=reject(negative) Tutorial - T-Test In this example, a T-Test analysis of type T-Paired is performed on the fictitious banking data to analyze account usage. Parameterize a Parametric Test analysis as follows: • Available Tables — twm_customer_analysis • Statistical Test Style — T Paired • First Column — avg_cc_bal • Second Column — avg_sv_bal Teradata Warehouse Miner User Guide - Volume 1 267 Chapter 3: Statistical Tests Parametric Tests • Group By Columns — age, gender • Analysis Parameters • Threshold Probability — 0.05 • Equal Variance — true (checked) Run the analysis and click on Results when it completes. For this example, the Parametric Test analysis generated the following page. The paired t-test was computed on average credit card balance vs. average savings balance, by gender and age. Ages over 33 were excluded for brevity. Results were sorted by age and gender in the listing below. The tests shows whether the paired values have mean differences which are not significantly different from zero for each gender-age combination. A ‘p’ means the difference was significantly different from zero. An ‘a’ means the difference was insignificant. The SQL is available for viewing but not listed below. Table 83: T-Test gender age D_F TTestPValue T TTestCallP_0.05 F 13 7 0.01 3.99 p M 13 6 0.13 1.74 a F 14 5 0.10 2.04 a M 14 8 0.04 2.38 p F 15 18 0.01 3.17 p M 15 12 0.04 2.29 p F 16 9 0.00 4.47 p M 16 8 0.04 2.52 p F 17 13 0.00 4.68 p M 17 6 0.01 3.69 p F 18 9 0.00 6.23 p M 18 9 0.02 2.94 p F 19 9 0.01 3.36 p M 19 6 0.03 2.92 p F 22 3 0.21 1.57 a M 22 3 0.11 2.25 a F 23 3 0.34 1.13 a M 23 3 0.06 2.88 a F 25 4 0.06 2.59 a F 26 5 0.08 2.22 a 268 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Table 83: T-Test gender age D_F TTestPValue T TTestCallP_0.05 F 27 5 0.09 2.12 a F 28 4 0.06 2.68 a M 28 4 0.03 3.35 p F 29 4 0.06 2.54 a M 29 5 0.16 1.65 a F 30 8 0.00 4.49 p M 30 5 0.01 4.25 p F 31 5 0.04 2.69 p M 31 6 0.05 2.52 p F 32 5 0.05 2.50 a M 32 6 0.10 1.98 a F 33 9 0.01 3.05 p M 33 4 0.09 2.27 a F-Test - N-Way • F-Test/Analysis of Variance — One Way, Equal or Unequal Sample Size • F-Test/Analysis of Variance — Two Way, Equal Sample Size • F-Test/Analysis of Variance — Three Way, Equal Sample Size The ANOVA or F test determines if significant differences exist among treatment means or interactions. It’s a preliminary test that indicates if further analysis of the relationship among treatment means is warranted. If the null hypothesis of no difference among treatments is accepted, the test result implies factor levels and response are unrelated, so the analysis is terminated. When the null hypothesis is rejected, the analysis is usually continued to examine the nature of the factor-level effects. Examples are: • Tukey’s Method — tests all possible pairwise differences of means • Scheffe’s Method — tests all possible contrasts at the same time • Bonferroni’s Method — tests, or puts simultaneous confidence intervals around a preselected group of contrasts The N-way F-Test is designed to execute within groups defined by the distinct values of the group-by variables (GBV's), the same as most of the other nonparametric tests. Two or more treatments must exist in the data within the groups defined by the distinct GBV values. Given a column of interest (dependent variable), one or more input columns (independent variables) and optionally one or more group-by columns (all from the same input table), an FTest is produced. The N-Way ANOVA tests whether a set of sample means are all equal (the Teradata Warehouse Miner User Guide - Volume 1 269 Chapter 3: Statistical Tests Parametric Tests null hypothesis). Output is a p-value which when compared to the user’s threshold, determines whether the null hypothesis should be rejected. Initiate an N-Way F-Test Use the following procedure to initiate a new F-Test analysis in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 175: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Parametric Tests: Figure 176: Add New Analysis > Statistical Tests > Parametric Tests 3 This will bring up the Parametric Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. F-Test (N-Way) - INPUT - Data Selection On the Parametric Tests dialog click on INPUT and then click on data selection: 270 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Figure 177: F-Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the parametric tests available (T, F(n-way), F(2-way with unequal cell counts) Select “F(n-way)”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Columns or Group By Columns. Make sure you have the correct portion of the window highlighted. • Column of Interest — The column that specifies the dependent variable for the Ftest analysis. • Columns — The column(s) that specifies the independent variable(s) for the F-test analysis. Selection of one column will generate a 1-Way F-test, two columns a 2Way F-test, and three columns a 3-Way F-test. Do not select over three columns because the 4-way, 5-way, etc. F-tests are not implemented in the version of TWM. Teradata Warehouse Miner User Guide - Volume 1 271 Chapter 3: Statistical Tests Parametric Tests Warning: For this test, equal cell counts are required for the 2 and 3 way tests. • Group By Columns — The column(s) that specifies the variable(s) whose distinct value combinations will categorize the data, so a separate test is performed on each category. F-Test (N-Way) - INPUT - Analysis Parameters On the Parametric Tests dialog click on INPUT and then click on analysis parameters: Figure 178: F-Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. F-Test - OUTPUT On the Parametric Tests dialog click on OUTPUT: Figure 179: F-Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: 272 • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the F-Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - F-Test Analysis The results of running the F-test analysis include a table with a row for each group-by variable requested, as well as the SQL to perform the statistical analysis. All of these results are outlined below. F-Test - RESULTS - SQL On the Parametric Tests dialog click on RESULTS and then click on SQL: Figure 180: F-Test > Results > SQL Teradata Warehouse Miner User Guide - Volume 1 273 Chapter 3: Statistical Tests Parametric Tests The series of SQL statements comprise the F-test Analysis. It is always returned, and is the only item returned when the Generate SQL Without Executing option is used. F-Test - RESULTS - data On the Parametric Tests dialog click on RESULTS and then click on data: Figure 181: F-Test > Results > data The output table is generated by the F-test Analysis for each group-by variable combination. Output Columns - F-Test Analysis The particular result table returned will depend on whether the test is 1-way, 2-way or 3-way, and is built in the requested Output Database by the F-test analysis. If group-by columns are present, they will comprise the Unique Primary Index (UPI). Otherwise DF will be the UPI. Table 84: Output Columns - 1-Way F-Test Analysis Name Type Definition DF INTEGER Degrees of Freedom for the Variable DFErr INTEGER Degrees of Freedom for Error F Float The computed value of the F statistic FPValue Float The probability associated with the F statistic FPText Char If not NULL, the probability is less than the smallest or more than the largest table value FCallP Char The F-Test result: a=accept, p=reject (positive), n=reject(negative) Table 85: Output Columns - 2-Way F-Test Analysis Name Type Definition DF INTEGER Degrees of Freedom for the model Fmodel Float The computed value of the F statistic for the model DFErr INTEGER Degrees of Freedom for Error term DF_1 INTEGER Degrees of Freedom for first variable F1 Float The computed value of the F statistic for the first variable 274 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Table 85: Output Columns - 2-Way F-Test Analysis Name Type Definition DF_2 INTEGER Degrees of Freedom for second variable F2 Float The computed value of the F statistic for the second variable DF_12 INTEGER Degrees of Freedom for interaction F12 Float The computed value of the F statistic for interaction Fmodel_PValue Float The probability associated with the F statistic for the model Fmodel_PText Char If not NULL, the probability is less than the smallest or more than the largest table value Fmodel_CallP_0.05 Char The F test result: a=accept, p=reject for the model F1_PValue Float The probability associated with the F statistic for the first variable F1_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F1_callP_0.05 Char The F test result: a=accept, p=reject for the first variable F2_PValue Float The probability associated with the F statistic for the second variable F2_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F2_callP_0.05 Char The F test result: a=accept, p=reject for the second variable F12_PValue Float The probability associated with the F statistic for the interaction F12_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F12_callP_0.05 Char The F test result: a=accept, p=reject for the interaction Table 86: Output Columns - 3-Way F-Test Analysis Name Type Definition DF INTEGER Degrees of Freedom for the model Fmodel Float The computed value of the F statistic for the model DFErr INTEGER Degrees of Freedom for Error term DF_1 INTEGER Degrees of Freedom for first variable F1 Float The computed value of the F statistic for the first variable DF_2 INTEGER Degrees of Freedom for second variable F2 Float The computed value of the F statistic for the second variable DF_3 INTEGER Degrees of Freedom for third variable Teradata Warehouse Miner User Guide - Volume 1 275 Chapter 3: Statistical Tests Parametric Tests Table 86: Output Columns - 3-Way F-Test Analysis Name Type Definition F3 Float The computed value of the F statistic for the third variable DF_12 INTEGER Degrees of Freedom for interaction of v1 and v2 F12 Float The computed value of the F statistic for interaction of v1 and v2 DF_13 INTEGER Degrees of Freedom for interaction of v1 and v3 F13 Float The computed value of the F statistic for interaction of v1 and v3 DF_23 INTEGER Degrees of Freedom for interaction of v2 and v3 F23 Float The computed value of the F statistic for interaction of v2 and v3 DF_123 INTEGER Degrees of Freedom for three-way interaction of v1, v2, and v3 F123 Float The computed value of the F statistic for three-way interaction of v1, v2 and v3 Fmodel_PValue Float The probability associated with the F statistic for the model Fmodel_PText Char If not NULL, the probability is less than the smallest or more than the largest table value Fmodel_callP_0.05 Char The F test result: a=accept, p=reject for the model F1_PValue Float The probability associated with the F statistic for the first variable F1_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F1_callP_0.05 Char The F test result: a=accept, p=reject for the first variable F2_PValue Float The probability associated with the F statistic for the second variable F2_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F2_callP_0.05 Char The F test result: a=accept, p=reject for the second variable F3_PValue Float The probability associated with the F statistic for the third variable F3_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F3_callP_0.05 Char The F test result: a=accept, p=reject for the third variable F12_PValue Float The probability associated with the F statistic for the interaction of v1 and v2 F12_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F12_callP_0.05 Char The F test result: a=accept, p=reject for the interaction of v1 and v2 F13_PValue Float The probability associated with the F statistic for the interaction of v1 and v3 276 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Table 86: Output Columns - 3-Way F-Test Analysis Name Type Definition F13_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F13_callP_0.05 Char The F test result: a=accept, p=reject for the interaction of v1 and v3 F23_PValue Float The probability associated with the F statistic for the interaction of v2 and v3 F23_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F23_callP_0.05 Char The F test result: a=accept, p=reject for the interaction of v2 and v3 F123_PValue Float The probability associated with the F statistic for the three-way interaction of v1, v2 and v3 F123_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F123_callP_0.05 Char The F test result: a=accept, p=reject for the three-way interaction of v1, v2 and v3 Tutorial - One-Way F-Test Analysis In this example, an F-test analysis is performed on the fictitious banking data to analyze income by gender. Parameterize an F-Test analysis as follows: • Available Tables — twm_customer • Column of Interest — income • Columns — gender • Group By Columns — years_with_bank, nbr_children • Analysis Parameters • Threshold Probability — 0.01 Run the analysis and click on Results when it completes. For this example, the F-Test analysis generated the following page. The F-Test was computed on income over gender for every combination of years_with_bank and nbr_children. Results were sorted by years_with_bank and nbr_children in the listing below. The tests shows whether significant differences exist in income for males and females, and does so separately for each value of years_with_bank and nbr_children. A ‘p’ means the difference was significant, and an ‘a’ means it was not significant. If the field is null, it indicates there was insufficient data for the test. The SQL is available for viewing but not listed below. Teradata Warehouse Miner User Guide - Volume 1 277 Chapter 3: Statistical Tests Parametric Tests Table 87: F-Test (one-way) years_with_bank nbr_children DF DFErr F FPValue FPText FCallP_0.01 0 0 1 53 0.99 0.25 >0.25 a 0 1 1 8 1.87 0.22 a 0 2 1 10 1.85 0.22 a 0 3 1 6 0.00 0.25 >0.25 a 0 4 1 0 0 5 0 0 1 0 1 55 0.00 0.25 >0.25 a 1 1 1 6 0.00 0.25 >0.25 a 1 2 1 14 0.00 0.25 >0.25 a 1 3 1 2 0.50 0.25 >0.25 a 1 4 0 0 1 5 0 0 2 0 1 55 0.82 0.25 >0.25 a 2 1 1 14 1.54 0.24 2 2 1 14 0.07 0.25 >0.25 a 2 3 1 1 0.30 0.25 >0.25 a 2 4 0 0 2 5 0 0 3 0 1 49 0.05 0.25 >0.25 a 3 1 1 9 1.16 0.25 >0.25 a 3 2 1 10 0.06 0.25 >0.25 a 3 3 1 6 16.90 0.01 3 4 1 1 4.50 0.25 3 5 0 0 4 0 1 52 1.84 0.20 4 1 1 10 0.54 0.25 4 2 1 6 2.38 0.20 4 3 0 0 4 4 0 0 278 a p >0.25 a a >0.25 a a Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Table 87: F-Test (one-way) years_with_bank nbr_children DF DFErr F FPValue 4 5 0 1 5 0 1 5 1 5 FPText FCallP_0.01 46 4.84 0.04 1 15 0.48 0.25 2 1 10 3.51 0.09 a 5 3 1 2 2.98 0.24 a 5 4 0 0 6 0 1 46 0.01 0.25 6 1 1 14 3.67 0.08 6 2 1 15 0.13 0.25 6 3 0 0 6 5 0 0 7 0 1 41 4.99 0.03 7 1 1 8 0.01 0.25 >0.25 a 7 2 1 4 0.13 0.25 >0.25 a 7 3 1 2 0.04 0.25 >0.25 a 7 5 0 1 8 0 1 23 0.50 0.25 >0.25 a 8 1 1 7 0.38 0.25 >0.25 a 8 2 1 6 0.09 0.25 >0.25 a 8 3 1 0 8 5 0 0 9 0 1 26 0.07 0.25 >0.25 a 9 1 1 3 3.11 0.20 9 2 1 1 0.09 0.25 >0.25 a 9 3 1 1 0.12 0.25 >0.25 a a >0.25 >0.25 a a a >0.25 a a a F-Test/Analysis of Variance - Two Way Unequal Sample Size The ANOVA or F test determines if significant differences exist among treatment means or interactions. It’s a preliminary test that indicates if further analysis of the relationship among treatment means is warranted. If the null hypothesis of no difference among treatments is accepted, the test result implies factor levels and response are unrelated, so the analysis is Teradata Warehouse Miner User Guide - Volume 1 279 Chapter 3: Statistical Tests Parametric Tests terminated. When the null hypothesis is rejected, the analysis is usually continued to examine the nature of the factor-level effects. Examples are: • Tukey’s Method — tests all possible pairwise differences of means • Scheffe’s Method — tests all possible contrasts at the same time • Bonferroni’s Method — tests, or puts simultaneous confidence intervals around a preselected group of contrasts The 2-way Unequal Sample Size F-Test is designed to execute on the entire dataset. No group-by parameter is provided for this test, but if such a test is desired, multiple tests must be run on pre-prepared datasets with group-by variables in each as different constants. Two or more treatments must exist in the data within the dataset. (Note that this test will create a temporary work table in the Result Database and drop it at the end of processing, even if the Output option to “Store the tabular output of this analysis in the database” is not selected). Given a table name of tabulated values, an F-Test is produced. The N-Way ANOVA tests whether a set of sample means are all equal (the null hypothesis). Output is a p-value which when compared to the user’s threshold, determines whether the null hypothesis should be rejected. Initiate a 2-Way F-Test with Unequal Cell Counts Use the following procedure to initiate a new F-Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 182: Add New Analysis from toolbar 2 280 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Parametric Tests: Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Figure 183: Add New Analysis > Statistical Tests > Parametric Tests 3 This will bring up the Parametric Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. F-Test (Unequal Cell Counts) - INPUT - Data Selection On the Parametric Tests dialog click on INPUT and then click on data selection: Figure 184: F-Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis. Note that if an analysis is selected it must be one that creates a table or view for output since a volatile table cannot be processed with this Statistical Test Style. For more Teradata Warehouse Miner User Guide - Volume 1 281 Chapter 3: Statistical Tests Parametric Tests information, about referencing an analysis for input refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the parametric tests available (T, F(n-way), F(2-way with unequal cell counts). Select “F(2-way with unequal cell counts)”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, First Column or Second Column. Make sure you have the correct portion of the window highlighted. • Column of Interest — The column that specifies the dependent variable for the Ftest analysis. • First Column — The column that specifies the first independent variable for the Ftest analysis. • Second Column — The column that specifies the second independent variable for the F-test analysis. F-Test - INPUT - Analysis Parameters On the Parametric Tests dialog click on INPUT and then click on analysis parameters: Figure 185: F-Test > Input > Analysis Parameters On this screen enter or select: • Processing Options 282 • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. • First Column Values — Use the selection wizard to choose any or all of the values of the first independent variable to be used in the analysis. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests • Second Column Values — Use the selection wizard to choose any or all of the values of the second independent variable to be used in the analysis. F-Test - OUTPUT On the Parametric Tests dialog click on OUTPUT: Figure 186: F-Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Teradata Warehouse Miner User Guide - Volume 1 283 Chapter 3: Statistical Tests Parametric Tests Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the F-Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - F-Test Analysis The results of running the F-test analysis include a table with a single row, as well as the SQL to perform the statistical analysis. All of these results are outlined below. F-Test - RESULTS - SQL On the Parametric Tests dialog click on RESULTS and then click on SQL: Figure 187: F-Test > Results > SQL The series of SQL statements comprise the F-test Analysis. It is always returned, and is the only item returned when the Generate SQL Without Executing option is used. F-Test - RESULTS - data On the Parametric Tests dialog click on RESULTS and then click on data: Figure 188: F-Test > Results > data The output table is generated by the F-test Analysis for each group-by variable combination. Output Columns - F-Test Analysis The result table returned is built in the requested Output Database by the F-test analysis. DF will be the UPI. 284 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Parametric Tests Table 88: Output Columns - 2-Way F-Test Analysis Name Type Definition DF INTEGER Degrees of Freedom for the model Fmodel Float The computed value of the F statistic for the model DFErr INTEGER Degrees of Freedom for Error term DF_1 INTEGER Degrees of Freedom for first variable F1 Float The computed value of the F statistic for the first variable DF_2 INTEGER Degrees of Freedom for second variable F2 Float The computed value of the F statistic for the second variable DF_12 INTEGER Degrees of Freedom for interaction F12 Float The computed value of the F statistic for interaction Fmodel_PValue Float The probability associated with the F statistic for the model Fmodel_PText Char If not NULL, the probability is less than the smallest or more than the largest table value Fmodel_CallP_0.05 Char The F test result: a=accept, p=reject for the model F1_PValue Float The probability associated with the F statistic for the first variable F1_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F1_callP_0.05 Char The F test result: a=accept, p=reject for the first variable F2_PValue Float The probability associated with the F statistic for the second variable F2_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F2_callP_0.05 Char The F test result: a=accept, p=reject for the second variable F12_PValue Float The probability associated with the F statistic for the interaction F12_PText Char If not NULL, the probability is less than the smallest or more than the largest table value F12_callP_0.05 Char The F test result: a=accept, p=reject for the interaction Tutorial - Two-Way Unequal Cell Count F-Test Analysis In this example, an F-test analysis is performed on the fictitious banking data to analyze income by years_with_bank and marital_status. Parameterize an F-Test analysis as follows: • Available Tables — twm_customer • Column of Interest — income • First Column — years_with_bank • Second Column — marital_status Teradata Warehouse Miner User Guide - Volume 1 285 Chapter 3: Statistical Tests Binomial Tests • Analysis Parameters • Threshold Probability — 0.05 • First Column Values — 0, 1, 2, 3, 4, 5, 6, 7 • Second Column Values — 1, 2, 3, 4 Run the analysis and click on Results when it completes. For this example, the F-Test analysis generated the following page. The F-Test was computed on income over years_with_bank and marital_status. The test shows whether significant differences exist in income for years_with_bank by marital_status. The first column, years_with_bank, is represented by F1. The second column, marital_status, is represented by F2. The interaction term is F12. A ‘p’ means the difference was significant, and an ‘a’ means it was not significant. If the field is null, it indicates there was insufficient data for the test. The SQL is available for viewing but not listed below. The results show that there are no significant differences in income for different values of years_with_bank or the interaction term for years_with_bank and marital_status. There was a highly significant (p<0.001) difference in income for different values of marital status. The overall model difference was significant at a level better than 0.001. Table 89: F-Test (Two-way Unequal Cell Count) (Part 1) DF Fmodel DFErr DF_1 F1 DF_2 F2 DF_12 F12 31 3.76 631 7 0.93 3 29.02 21 1.09 Table 90: F-Test (Two-way Unequal Cell Count) (Part 2) Fmodel_PValue Fmodel_PText Fmodel_CallP_0.05 F1_PValue F1_PText F1_CallP_0.05 0.001 <0.001 p 0.25 >0.25 a Table 91: F-Test (Two-way Unequal Cell Count) (Part 3) F2_PValue F2_PText F2_CallP_0.05 F12_PValue F12_PText F12_CallP_0.05 0.001 <0.001 p 0.25 >0.25 a Binomial Tests The data for a binomial test is assumed to come from n independent trials, and have outcomes in either of two classes. The other assumption is that the probability of each outcome of each trial is the same, designated p. The values of the outcome could come directly from the data, where the value is always one of two kinds. More commonly, however, the test is applied to the sign of the difference between two values. If the probability is 0.5, this is the oldest of all 286 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Binomial Tests nonparametric tests, and is called the ‘sign test’. Where the sign of the difference between two values is used, the binomial test reports whether the probability that the sign is positive is a particular p_value, p*. Binomial/Ztest Output for each unique set of values of the group-by variables (GBV's) is a p-value which when compared to the user’s choice of alpha, the probability threshold, determines whether the null hypothesis (p=p*, p<=p*, or p>p*) should be rejected for the GBV set. Though both binomial and Ztest results are provided for all N, for the approximate value obtained from the Z-test (nP) is appropriate when N is large. For values of N over 100, only the Z-test is performed. Otherwise, the value bP returned is the p_value of the one-tailed or two-tailed test, depending on the user’s choice. Initiate a Binomial Test Use the following procedure to initiate a new Binomial in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 189: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Binomial Tests: Teradata Warehouse Miner User Guide - Volume 1 287 Chapter 3: Statistical Tests Binomial Tests Figure 190: Add New Analysis > Statistical Tests > Binomial Tests 3 This will bring up the Binomial Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Binomial Tests - INPUT - Data Selection On the Binomial Tests dialog click on INPUT and then click on data selection: Figure 191: Binomial Tests > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis 288 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Binomial Tests that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the binomial tests available (Binomial, Sign). Select “Binomial”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as First Column, Second Column or Group By Columns. Make sure you have the correct portion of the window highlighted. • First Column — The column that specifies the first variable for the Binomial Test analysis. • Second Column — The column that specifies the second variable for the Binomial Test analysis. • Group By Columns — The column(s) that specifies the variable(s) whose distinct value combinations will categorize the data, so a separate test is performed on each category. Binomial Tests - INPUT - Analysis Parameters On the Binomial Tests dialog click on INPUT and then click on analysis parameters: Figure 192: Binomial Tests > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. • Single Tail — Check this box if the Binomial Test is to be single tailed. Default is twotailed. Teradata Warehouse Miner User Guide - Volume 1 289 Chapter 3: Statistical Tests Binomial Tests • Binomial Probability — If the binomial test is not ½, enter the probability desired. Default is 0.5. • Exact Matches Comparison Criterion — Check the button to specify how exact matches are to be handled. Default is they are discarded. Other options are to include them with negative count, or with positive count. Binomial Tests - OUTPUT On the Binomial Tests dialog click on OUTPUT: Figure 193: Binomial Tests > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: 290 • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Binomial Tests and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the Binomial Sign Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Binomial Test The results of running the Binomial analysis include a table with a row for each group-by variable requested, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Binomial Tests - RESULTS - SQL On the Binomial Tests dialog click on RESULTS and then click on SQL: Figure 194: Binomial Tests > Results > SQL The series of SQL statements comprise the Binomial Analysis. It is always returned, and is the only item returned when the Generate SQL Without Executing option is used. Binomial Tests - RESULTS - data On the Binomial Tests dialog click on RESULTS and then click on data: Figure 195: Binomial Tests > Results > data Teradata Warehouse Miner User Guide - Volume 1 291 Chapter 3: Statistical Tests Binomial Tests The output table is generated by the Binomial Analysis for each group-by variable combination. Output Columns - Binomial Tests The following table is built in the requested Output Database by the Binomial analysis. Any group-by columns will comprise the Unique Primary Index (UPI), otherwise the UPI will be “N”. Table 92: Output Database table (Built by the Binomial Analysis) Name Type Definition N INTEGER Total count of value pairs NPos INTEGER Count of positive value differences NNeg INTEGER Count of negative value differences BP FLOAT The Binomial Probability BinomialCallP Char The Binomial result: a=accept, p=reject (positive), n=reject(negative) Tutorial - Binomial Tests Analysis In this example, an Binomial analysis is performed on the fictitious banking data to analyze account usage. Parameterize the Binomial analysis as follows: • Available Tables — twm_customer_analysis • First Column — avg_sv_bal • Second Column — avg_ck_bal • Group By Columns — gender • Analysis Parameters • Threshold Probability — 0.05 • Single Tail — true • Binomial Probability — 0.5 • Exact Matches — discarded Run the analysis and click on Results when it completes. For this example, the Binomial analysis generated the following. The Binomial was computed on average savings balance (column 1) vs. average check account balance (column 2), by gender. The test is a Z Test since N>100, and Z is 3.29 (not in answer set) so the one-sided test of the null hypothesis that p is ½ is rejected as shown in the table below. Table 93: Binomial Test Analysis (Table 1) gender N NPos NNeg BP BinomialCallP_0.05 F 366 217 149 0.0002 p M 259 156 103 0.0005 p 292 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Binomial Tests Rerunning the test with parameter binomial probability set to 0.6 gives a different result: the one-sided test of the null hypothesis that p is 0.6 is accepted as shown in the table below. Table 94: Binomial Test Analysis (Table 2) gender N NPos NNeg BP BinomialCallP_0.05 F 366 217 149 0.3909 a M 259 156 103 0.4697 a Binomial Sign Test For the sign test, one column is selected and the test is whether the value is positive or not positive. Initiate a Binomial Sign Test Use the following procedure to initiate a new Binomial Sign Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 196: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Binomial Tests: Teradata Warehouse Miner User Guide - Volume 1 293 Chapter 3: Statistical Tests Binomial Tests Figure 197: Add New Analysis > Statistical Tests > Binomial Tests 3 This will bring up the Binomial Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Binomial Sign Test - INPUT - Data Selection On the Binomial Tests dialog click on INPUT and then click on data selection: Figure 198: Binomial Sign Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis 294 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Binomial Tests that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the binomial tests available (Binomial, Sign). Select “Sign”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. • Column/Group By Columns — Note that the Selected Columns window is actually a split window; you can insert columns as Column, or Group By Columns. Make sure you have the correct portion of the window highlighted. • Column — The column that specifies the first variable for the Binomial Test analysis. • Group By Columns — The column(s) that specifies the variable(s) whose distinct value combinations will categorize the data, so a separate test is performed on each category. Binomial Sign Test - INPUT - Analysis Parameters On the Binomial Tests dialog click on INPUT and then click on analysis parameters: Figure 199: Binomial Sign Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. • Single Tail — Check this box if the Binomial Test is to be single tailed. Default is twotailed. Binomial Sign Test - OUTPUT On the Binomial Tests dialog click on OUTPUT: Teradata Warehouse Miner User Guide - Volume 1 295 Chapter 3: Statistical Tests Binomial Tests Figure 200: Binomial Sign Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: 296 • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Binomial Tests Run the Binomial Sign Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Binomial Sign Test Analysis The results of running the Binomial Sign analysis include a table with a row for each groupby variable requested, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Binomial Sign Test - RESULTS - SQL On the Binomial Tests dialog click on RESULTS and then click on SQL: Figure 201: Binomial Sign Test > Results > SQL The series of SQL statements comprise the Binomial Sign Analysis. It is always returned, and is the only item returned when the Generate SQL Without Executing option is used. Binomial Sign Test - RESULTS - data On the Binomial Tests dialog click on RESULTS and then click on data: Figure 202: Binomial Sign Test > Results > data The output table is generated by the Binomial Sign Analysis for each group-by variable combination. Output Columns - Binomial Sign Analysis The following table is built in the requested Output Database by the Binomial analysis. Any group-by columns will comprise the Unique Primary Index (UPI), otherwise the UPI will be “N”. Teradata Warehouse Miner User Guide - Volume 1 297 Chapter 3: Statistical Tests Binomial Tests Table 95: Binomial Sign Analysis: Output Columns Name Type Definition N INTEGER Total count of value pairs NPos INTEGER Count of positive values NNeg INTEGER Count of negative or zero values BP FLOAT The Binomial Probability BinomialCallP Char The Binomial Sign result: a=accept, p=reject (positive), n=reject(negative) Tutorial - Binomial Sign Analysis In this example, a Binomial analysis is performed on the fictitious banking data to analyze account usage. Parameterize the Binomial analysis as follows: • Available Tables — twm_customer_analysis • Column — female • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.05 • Single Tail — true Run the analysis and click on Results when it completes. For this example, the Binomial Sign analysis generated the following. The Binomial was computed on the Boolean variable “female” by years_with_bank. The one-sided test of the null hypothesis that p is ½ accepted for all cases except years_with_bank=2 as shown in the table below. Table 96: Tutorial - Binomial Sign Analysis years_with_bank N NPos NNeg BP BinomialCallP_0.05 0 88 51 37 0.08272 a 1 87 48 39 0.195595 a 2 94 57 37 0.024725 p 3 86 46 40 0.295018 a 4 78 39 39 0.545027 a 5 82 46 36 0.160147 a 6 83 46 37 0.19 a 7 65 36 29 0.22851 a 8 45 26 19 0.185649 a 9 39 23 16 0.168392 a 298 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Kolmogorov-Smirnov Tests Tests of the Kolmogorov-Smirnov Type are based on statistical procedures which use maximum vertical distance between functions as a measure of function similarity. Two empirical distribution functions are mapped against each other, or a single empirical function is mapped against a hypothetical (e.g. Normal) distribution. Conclusions are then drawn about the likelihood the two distributions are the same. Kolmogorov-Smirnov Test (One Sample) The Kolmogorov-Smirnov (one-sample) test determines whether a dataset matches a particular distribution (for this test, the normal distribution). The test has the advantage of making no assumption about the distribution of data. (Non-parametric and distribution free) Note that this generality comes at some cost: other tests (e.g. the Student's t-test) may be more sensitive if the data meet the requirements of the test. The Kolmogorov-Smirnov test is generally less powerful than the tests specifically designed to test for normality. This is especially true when the mean and variance are not specified in advance for the KolmogorovSmirnov test, which then becomes conservative. Further, the Kolmogorov-Smirnov test will not indicate the type of nonnormality, e.g. whether the distribution is skewed or heavy-tailed. Examination of the skewness and kurtosis, and of the histogram, boxplot, and normal probability plot for the data may show why the data failed the Kolmogorov-Smirnov test. In this test, the user can specify group-by variables (GBV's) so a separate test will be done for every unique set of values of the GBV's. Initiate a Kolmogorov-Smirnov Test Use the following procedure to initiate a new Kolmogorov-Smirnov Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 203: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Kolmogorov-Smirnov Tests: Teradata Warehouse Miner User Guide - Volume 1 299 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Figure 204: Add New Analysis > Statistical Tests > Kolmogorov-Smirnov Tests 3 This will bring up the Kolmogorov-Smirnov Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Kolmogorov-Smirnov Test - INPUT - Data Selection On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on data selection: Figure 205: Kolmogorov-Smirnov Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis 300 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests of the Kolmogorov-Smirnov Type available (Kolmogorov-Smirnov, Lilliefors, Shapiro-Wilk, D'Agostino-Pearson, Smirnov). Select “Kolmogorov-Smirnov”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Group By Columns. Make sure you have the correct portion of the window highlighted. • Column of Interest — The column that specifies the numeric variable to be tested for normality. • Group By Columns — The columns which specify the variables whose distinct value combinations will categorize the data, so a separate test is performed on each category. Kolmogorov-Smirnov Test - INPUT - Analysis Parameters On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on analysis parameters: Figure 206: Kolmogorov-Smirnov Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. Kolmogorov-Smirnov Test - OUTPUT On the Kolmogorov-Smirnov Tests dialog click on OUTPUT: Teradata Warehouse Miner User Guide - Volume 1 301 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Figure 207: Kolmogorov-Smirnov Test > Output On this screen select: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: 302 • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Run the Kolmogorov-Smirnov Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Kolmogorov-Smirnov Test The results of running the Kolmogorov-Smirnov Test analysis include a table with a row for each separate Kolmogorov-Smirnov test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Kolmogorov-Smirnov Test - RESULTS - SQL On the Kolmogorov-Smirnov Test dialog click on RESULTS and then click on SQL: Figure 208: Kolmogorov-Smirnov Test > Results > SQL The series of SQL statements comprise the Kolmogorov-Smirnov Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Kolmogorov-Smirnov Test - RESULTS - data On the Kolmogorov-Smirnov Test dialog click on RESULTS and then click on data: Figure 209: Kolmogorov-Smirnov Test > Results > Data The output table is generated by the Analysis for each separate Kolmogorov-Smirnov test on all distinct-value group-by variables. Output Columns - Kolmogorov-Smirnov Test Analysis The following table is built in the requested Output Database by the Kolmogorov-Smirnov test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise Klm will be the UPI. Teradata Warehouse Miner User Guide - Volume 1 303 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Table 97: Output Database table (Built by the Kolmogorov-Smirnov test analysis) Name Type Definition Klm Float Kolmogorov-Smirnov Value M INTEGER Count KlmPValue Float The probability associated with the Kolmogorov-Smirnov statistic KlmPText Char Text description if P is outside table range KlmCallP_0.05 Char The Kolmogorov-Smirnov result: a=accept, p=reject Tutorial - Kolmogorov-Smirnov Test Analysis In this example, a Kolmogorov-Smirnov test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Kolmogorov-Smirnov Test analysis as follows: • Available Tables — twm_customer_analysis • Column of Interest — income • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.05 Run the analysis and click on Results when it completes. For this example, the KolmogorovSmirnov Test analysis generated the following table. The Kolmogorov-Smirnov Test was computed for each distinct value of the group by variable “years_with_bank”. Results were sorted by years_with_bank. The tests shows customer incomes with years_with_bank of 1, 5,6,7,8, and 9 were normally distributed and those with 0, 2, and 3 were not. A ‘p’ means significantly nonnormal and an ‘a’ means accept the null hypothesis of normality. The SQL is available for viewing but not listed below. Table 98: Kolmogorov-Smirnov Test years_with_bank Klm M KlmPValue 0 0.159887652 88 0.019549995 p 1 0.118707332 87 0.162772589 a 2 0.140315991 94 0.045795894 p 3 0.15830739 86 0.025080666 p 4 0.999999 78 0.01 5 0.138336567 82 0.080579955 a 6 0.127171093 83 0.127653475 a 7 0.135147555 65 0.172828265 a 8 0.184197592 45 0.084134345 a 304 KlmPText <0.01 KlmCallP_0.05 p Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Table 98: Kolmogorov-Smirnov Test years_with_bank Klm M KlmPValue KlmPText KlmCallP_0.05 9 0.109205054 39 0.20 >0.20 a Lilliefors Test The Lilliefors test determines whether a dataset matches a particular distribution, and is identical to the Kolmogorov-Smirnov test except that conversion to Z-scores is made. The Lilliefors test is therefore a modification of the Kolmogorov-Smirnov test. The Lilliefors test computes the Lilliefors statistic and checks its significance. Exact tables of the quantiles of the test statistic were computed from random numbers in computer simulations. The computed value of the test statistic is compared with the quantiles of the statistic. When the test is for the normal distribution, the null hypothesis is that the distribution function is normal with unspecified mean and variance. The alternative hypothesis is that the distribution function is nonnormal. The empirical distribution of X is compared with a normal distribution with the same mean and variance as X. It is similar to the Kolmogorov-Smirnov test, but it adjusts for the fact that the parameters of the normal distribution are estimated from X rather than specified in advance. In this test, the user can specify group-by variables (GBV's) so a separate test will be done for every unique set of values of the GBV's. Initiate a Lilliefors Test Use the following procedure to initiate a new Lilliefors Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 210: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Kolmogorov-Smirnov Tests: Teradata Warehouse Miner User Guide - Volume 1 305 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Figure 211: Add New Analysis> Statistical Tests > Kolmogorov-Smirnov Tests 3 This will bring up the Kolmogorov-Smirnov Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Lilliefors Test - INPUT - Data Selection On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on data selection: Figure 212: Lillefors Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis 306 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests of the Kolmogorov-Smirnov Type available (Kolmogorov-Smirnov, Lilliefors, Shapiro-Wilk, D'Agostino-Pearson, Smirnov). Select “Lilliefors”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Group By Columns. Make sure you have the correct portion of the window highlighted. • Column of Interest — The column that specifies the numeric variable to be tested for normality. • Group By Columns — The columns which specify the variables whose distinct value combinations will categorize the data, so a separate test is performed on each category. Lilliefors Test - INPUT - Analysis Parameters On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on analysis parameters: Figure 213: Lillefors Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. Lilliefors Test - OUTPUT On the Kolmogorov-Smirnov Tests dialog click on OUTPUT: Teradata Warehouse Miner User Guide - Volume 1 307 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Figure 214: Lillefors Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: 308 • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Run the Lilliefors Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Lilliefors Test Analysis The results of running the Lilliefors Test analysis include a table with a row for each separate Lilliefors test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Lilliefors Test - RESULTS - SQL On the Kolmogorov-Smirnov Tests dialog click on RESULTS and then click on SQL: Figure 215: Lillefors Test > Results > SQL The series of SQL statements comprise the Lilliefors Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Lilliefors Test - RESULTS - Data On the Kolmogorov-Smirnov Tests dialog click on RESULTS and then click on data: Figure 216: Lillefors Test > Results > Data The output table is generated by the Analysis for each separate Lilliefors test on all distinctvalue group-by variables. Output Columns - Lilliefors Test Analysis The following table is built in the requested Output Database by the Lilliefors test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise Lilliefors will be the UPI. Teradata Warehouse Miner User Guide - Volume 1 309 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Table 99: Lilliefors Test Analysis: Output Columns Name Type Definition Lilliefors Float Lilliefors Value M INTEGER Count LillieforsPValue Float The probability associated with the Lilliefors statistic LillieforsPText Char Text description if P is outside table range LillieforsCallP_0.05 Char The Lilliefors result: a=accept, p=reject Tutorial - Lilliefors Test Analysis In this example, a Lilliefors test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Lilliefors Test analysis as follows: • Available Tables — twm_customer_analysis • Column of Interest — income • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.05 Run the analysis and click on Results when it completes. For this example, the Lilliefors Test analysis generated the following table. The Lilliefors Test was computed for each distinct value of the group by variable “years_with_bank”. Results were sorted by years_with_bank. The tests show customer all incomes were not normally distributed. ‘p’ means significantly nonnormal and an ‘a’ means accept the null hypothesis of normality. Note: The SQL is available for viewing but not listed below. Table 100: Lilliefors Test years_with_bank Lilliefors M LillieforsPValue LillieforsPText LillieforsCallP_0.05 0 0.166465166 88 0.01 <0.01 p 1 0.123396019 87 0.01 <0.01 p 2 0.146792366 94 0.01 <0.01 p 3 0.156845809 86 0.01 <0.01 p 4 0.192756959 78 0.01 <0.01 p 5 0.144308699 82 0.01 <0.01 p 6 0.125268495 83 0.01 <0.01 p 7 0.141128127 65 0.01 <0.01 p 8 0.191869596 45 0.01 <0.01 p 310 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Table 100: Lilliefors Test years_with_bank Lilliefors M LillieforsPValue LillieforsPText LillieforsCallP_0.05 9 0.111526787 39 0.20 >0.20 a Shapiro-Wilk Test The Shapiro-Wilk W test is designed to detect departures from normality without requiring that the mean or variance of the hypothesized normal distribution be specified in advance. It is considered to be one of the best omnibus tests of normality. The function is based on the approximations and code given by Royston (1982a, b). It can be used in samples as large as 2,000 or as small as 3. Royston (1982b) gives approximations and tabled values that can be used to compute the coefficients, and obtains the significance level of the W statistic. Small values of W are evidence of departure from normality. This test has done very well in comparison studies with other goodness of fit tests. In general, either the Shapiro-Wilk or D'Agostino-Pearson test is a powerful overall test for normality. As omnibus tests, however, they will not indicate the type of nonnormality, e.g. whether the distribution is skewed as opposed to heavy-tailed (or both). Examination of the calculated skewness and kurtosis, and of the histogram, boxplot, and normal probability plot for the data may provide clues as to why the data failed the Shapiro-Wilk or D'AgostinoPearson test. The standard algorithm for the Shapiro-Wilk test only applies to sample sizes from 3 to 2000. For larger sample sizes, a different normality test should be used. The test statistic is based on the Kolmogorov-Smirnov statistic for a normal distribution with the same mean and variance as the sample mean and variance. Initiate a Shapiro-Wilk Test Use the following procedure to initiate a new Shapiro-Wilk Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 217: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Kolmogorov-Smirnov Tests: Teradata Warehouse Miner User Guide - Volume 1 311 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Figure 218: Add New Analysis > Statistical Tests > Kolmogorov-Smirnov Tests 3 This will bring up the Kolmogorov-Smirnov Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Shapiro-Wilk Test - INPUT - Data Selection On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on data selection: Figure 219: Shapiro-Wilk Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis 312 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests of the Kolmogorov-Smirnov Type available (Kolmogorov-Smirnov, Lilliefors, Shapiro-Wilk, D'Agostino-Pearson, Smirnov). Select “Shapiro-Wilk”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Group By Columns. Make sure you have the correct portion of the window highlighted. • Column of Interest — The column that specifies the numeric variable to be tested for normality. • Group By Columns — The columns which specify the variables whose distinct value combinations will categorize the data, so a separate test is performed on each category. Shapiro-Wilk Test - INPUT - Analysis Parameters On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on analysis parameters: Figure 220: Shapiro-Wilk Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. Shapiro-Wilk Test - OUTPUT On the Kolmogorov-Smirnov Tests dialog click on OUTPUT: Teradata Warehouse Miner User Guide - Volume 1 313 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Figure 221: Shapiro-Wilk Test > Output On this screen select: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: 314 • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Run the Shapiro-Wilk Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Shapiro-Wilk Analysis The results of running the Shapiro-Wilk Test analysis include a table with a row for each separate Shapiro-Wilk test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Shapiro-Wilk Test - RESULTS - SQL On the Kolmogorov-Smirnov Tests dialog click on RESULTS and then click on SQL: Figure 222: Shapiro-Wilk Test > Results > SQL The series of SQL statements comprise the Shapiro-Wilk Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Shapiro-Wilk Test - RESULTS - data On the Kolmogorov-Smirnov Tests dialog click on RESULTS and then click on data: Figure 223: Shapiro-Wilk Test > Results > data The output table is generated for each separate Shapiro-Wilk test on all distinct-value groupby variables. Output Columns - Shapiro-Wilk Test Analysis The following table is built in the requested Output Database by the Shapiro-Wilk test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise Shw will be the UPI. Teradata Warehouse Miner User Guide - Volume 1 315 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Table 101: Shapiro-Wilk Test Analysis: Output Columns Name Type Definition Shw Float Shapiro-Wilk Value N INTEGER Count ShapiroWilkPValue Float The probability associated with the Shapiro-Wilk statistic ShapiroWilkPText Char Text description if P is outside table range ShapiroWilkCallP_0.05 Char The Shapiro-Wilk result: a=accept, p=reject Tutorial - Shapiro-Wilk Test Analysis In this example, a Shapiro-Wilk test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Shapiro-Wilk Test analysis as follows: • Available Tables — twm_customer_analysis • Column of Interest — income • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.05 Run the analysis and click on Results when it completes. For this example, the Shapiro-Wilk Test analysis generated the following table. The Shapiro-Wilk Test was computed for each distinct value of the group by variable “years_with_bank”. Results were sorted by years_ with_bank. The tests show customer all incomes were not normally distributed. ‘p’ means significantly nonnormal and an ‘a’ means accept the null hypothesis of normality. Note: The SQL is available for viewing but not listed below. Table 102: Shapiro-Wilk Test years_with_bank Shw N ShapiroWilkPValue 0 0.84919004 88 0.000001 p 1 0.843099681 87 0.000001 p 2 0.831069533 94 0.000001 p 3 0.838965439 86 0.000001 p 4 0.707924134 78 0.000001 p 5 0.768444329 82 0.000001 p 6 0.855276885 83 0.000001 p 7 0.827399691 65 0.000001 p 8 0.863932178 45 0.01 316 ShapiroWilkPText <0.01 ShapiroWilkCallP_0.05 p Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Table 102: Shapiro-Wilk Test years_with_bank Shw N ShapiroWilkPValue 9 0.930834522 39 0.029586304 ShapiroWilkPText ShapiroWilkCallP_0.05 p D'Agostino and Pearson Test In general, either the Shapiro-Wilk or D'Agostino-Pearson test is a powerful overall test for normality. These tests are designed to detect departures from normality without requiring that the mean or variance of the hypothesized normal distribution be specified in advance. Though these tests cannot indicate the type of nonnormality, they tend to be more powerful than the Kolmogorov-Smirnov test. The D'Agostino-Pearson Ksquared statistic has approximately a chi-squared distribution with 2 df when the population is normally distributed. Initiate a D'Agostino and Pearson Test Use the following procedure to initiate a new D'Agostino and Pearson Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 224: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Kolmogorov-Smirnov Tests: Teradata Warehouse Miner User Guide - Volume 1 317 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Figure 225: Add New Analysis > Statistical Tests > Kolmogorov-Smirnov Tests 3 This will bring up the Kolmogorov-Smirnov Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. D'Agostino and Pearson Test - INPUT - Data Selection On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on data selection: Figure 226: D'Agostino and Pearson Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis 318 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests of the Kolmogorov-Smirnov Type available (Kolmogorov-Smirnov, Lilliefors, Shapiro-Wilk, D'Agostino-Pearson, Smirnov). Select “D'Agostino and Pearson”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Group By Columns. Make sure you have the correct portion of the window highlighted. • Column of Interest — The column that specifies the numeric variable to be tested for normality. • Group By Columns — The columns which specify the variables whose distinct value combinations will categorize the data, so a separate test is performed on each category. D'Agostino and Pearson Test - INPUT - Analysis Parameters On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on analysis parameters: Figure 227: D'Agostino and Pearson Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. Teradata Warehouse Miner User Guide - Volume 1 319 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests D'Agostino and Pearson Test - OUTPUT On the Kolmogorov-Smirnov Tests dialog click on OUTPUT: Figure 228: D'Agostino and Pearson Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: 320 • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the D'Agostino and Pearson Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - D'Agostino and Pearson Test Analysis The results of running the D'Agostino and Pearson Test analysis include a table with a row for each separate D'Agostino and Pearson test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. D'Agostino and Pearson Test - RESULTS - SQL On the Kolmogorov-Smirnov Tests dialog click on RESULTS and then click on SQL: Figure 229: D'Agostino and Pearson Test > Results > SQL The series of SQL statements comprise the D'Agostino and Pearson Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. D'Agostino and Pearson Test - RESULTS - data On the Kolmogorov-Smirnov Tests dialog click on RESULTS and then click on data: Figure 230: D'Agostino and Pearson Test > Results > data The output table is generated by the Analysis for each separate D'Agostino and Pearson test on all distinct-value group-by variables. Teradata Warehouse Miner User Guide - Volume 1 321 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Output Columns - D'Agostino and Pearson Test Analysis The following table is built in the requested Output Database by the D'Agostino and Pearson test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise T will be the UPI. Table 103: D'Agostino and Pearson Test Analysis: Output Columns Name Type Definition T Float K-Squared statistic Zkurtosis Float Z of kurtosis Zskew Float Z of Skewness ChiPValue Float The probability associated with the K-Squared statistic ChiPText Char Text description if P is outside table range ChiCallP_0.05 Char The D'Agostino-Pearson result: a=accept, p=reject Tutorial - D'Agostino and Pearson Test Analysis In this example, a D'Agostino and Pearson test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a D'Agostino and Pearson Test analysis as follows: • Available Tables — twm_customer_analysis • Column of Interest — income • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.05 Run the analysis and click on Results when it completes. For this example, the D'Agostino and Pearson Test analysis generated the following table. The D'Agostino and Pearson Test was computed for each distinct value of the group by variable “years_with_bank”. Results were sorted by years_with_bank. The tests show customer all incomes were not normally distributed except those from years_with_bank = 9. ‘p’ means significantly nonnormal and an ‘a’ means accept the null hypothesis of normality. The SQL is available for viewing but not listed below. Table 104: D'Agostino and Pearson Test: Output Columns years_with_bank T Zkurtosis Zskew ChiPValue ChiPText ChiCallP_0.05 0 29.05255 2.71261 4.65771 0.0001 <0.0001 p 1 34.18025 3.30609 4.82183 0.0001 <0.0001 p 2 30.71123 2.78588 4.79062 0.0001 <0.0001 p 3 32.81104 3.06954 4.83621 0.0001 <0.0001 p 322 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Table 104: D'Agostino and Pearson Test: Output Columns years_with_bank T Zkurtosis Zskew ChiPValue ChiPText ChiCallP_0.05 4 82.01928 5.72010 7.02137 0.0001 <0.0001 p 5 62.36861 4.91949 6.17796 0.0001 <0.0001 p 6 24.80241 2.40521 4.36089 0.0001 <0.0001 p 7 17.72275 1.83396 3.78937 0.00019 p 8 6.55032 -0.23415 2.54863 0.03992 p 9 3.32886 -0.68112 1.69261 0.20447 a Smirnov Test The Smirnov test (aka “two-sample Kolmogorov-Smirnov test”) checks whether two datasets have a significantly different distribution. The tests have the advantage of making no assumption about the distribution of data. (non-parametric and distribution free). Note that this generality comes at some cost: other tests (e.g. the Student's t-test) may be more sensitive if the data meet the requirements of the test. Initiate a Smirnov Test Use the following procedure to initiate a new Smirnov Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 231: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Kolmogorov-Smirnov Tests: Teradata Warehouse Miner User Guide - Volume 1 323 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Figure 232: Add New Analysis > Statistical Tests > Kolmogorov-Smirnov Tests 3 This will bring up the Kolmogorov-Smirnov Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Smirnov Test - INPUT - Data Selection On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on data selection: Figure 233: Smirnov Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis 324 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests of the Kolmogorov-Smirnov Type available (Kolmogorov-Smirnov, Lilliefors, Shapiro-Wilk, D'Agostino-Pearson, Smirnov). Select “Smirnov”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Columns, Group By Columns. Make sure you have the correct portion of the window highlighted. • Column of Interest — The column that specifies the numeric variable to be tested for normality. • Columns — The column specifying the 2-category variable that identifies the distribution to which the column of interest belongs. • Group By Columns — The columns which specify the variables whose distinct value combinations will categorize the data, so a separate test is performed on each category. Smirnov Test - INPUT - Analysis Parameters On the Kolmogorov-Smirnov Tests dialog click on INPUT and then click on analysis parameters: Figure 234: Smirnov Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. Teradata Warehouse Miner User Guide - Volume 1 325 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Smirnov Test - OUTPUT On the Kolmogorov-Smirnov Tests dialog click on OUTPUT: Figure 235: Smirnov Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: 326 • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the Smirnov Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Smirnov Test Analysis The results of running the Smirnov Test analysis include a table with a row for each separate Smirnov test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Smirnov Test - RESULTS - SQL On the Kolmogorov-Smirnov Tests dialog click on RESULTS and then click on SQL: Figure 236: Smirnov Test > Results > SQL The series of SQL statements comprise the Smirnov Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Smirnov Test - RESULTS - data On the Kolmogorov-Smirnov Tests dialog click on RESULTS and then click on data: Figure 237: Smirnov Test > Results > data The output table is generated by the Analysis for each separate Smirnov test on all distinctvalue group-by variables. Output Columns - Smirnov Test Analysis The following table is built in the requested Output Database by the Smirnov test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise M will be the UPI. Teradata Warehouse Miner User Guide - Volume 1 327 Chapter 3: Statistical Tests Kolmogorov-Smirnov Tests Table 105: Smirnov Test Analysis: Output Columns Name Type Definition M Integer Number of first distribution observations N Integer Number of second distribution observations D Float D Statistic SmirnovPValue Float The probability associated with the D statistic SmirnovPText Char Text description if P is outside table range SmirnovCallP_0.01 Char The D'Agostino-Pearson result: a=accept, p=reject Tutorial - Smirnov Test Analysis In this example, a Smirnov test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Smirnov Test analysis as follows: • Available Tables — twm_customer • Column of Interest — income • Columns — gender • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.05 Run the analysis and click on Results when it completes. For this example, the Smirnov Test analysis generated the following table. The Smirnov Test was computed for each distinct value of the group by variable “years_with_bank”. Results were sorted by years_with_bank. The tests show distributions of incomes of males and females were different for all values of years_with_bank. ‘p’ means significantly nonnormal and an ‘a’ means accept the null hypothesis of normality. The SQL is available for viewing but not listed below. Table 106: Smirnov Test years_with_bank M N D SmirnovPValue 0 37 51 1.422949567 0.000101 p 1 39 48 1.371667516 0.000103 p 2 37 57 1.465841724 0.000101 p 3 40 46 1.409836326 0.000105 p 4 39 39 1.397308541 0.000146 p 5 36 46 1.309704108 0.000105 p 6 37 46 1.287964978 0.000104 p 7 29 36 1.336945293 0.000112 p 328 SmirnovPText SmirnovCallP_0.01 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Tests Based on Contingency Tables Table 106: Smirnov Test years_with_bank M N D SmirnovPValue SmirnovPText SmirnovCallP_0.01 8 19 26 1.448297864 0.00011 p 9 16 23 1.403341724 0.000101 p Tests Based on Contingency Tables Tests Based on Contingency Tables are based on an array or matrix of numbers which represent counts or frequencies. The tests basically evaluate the matrix to detect if there is a nonrandom pattern of frequencies. Chi Square Test The most common application for chi-square is in comparing observed counts of particular cases to the expected counts. For example, a random sample of people would contain m males and f females but usually we would not find exactly m=½N and f=½N. We could use the chisquared test to determine if the difference were significant enough to rule out the 50/50 hypothesis. The Chi Square Test determines whether the probabilities observed from data in a RxC contingency table are the same or different. The null hypothesis is that probabilities observed are the same. Output is a p-value which when compared to the user’s threshold, determines whether the null hypothesis should be rejected. Other Calculated Measures of Association • Phi coefficient — The Phi coefficient is a measure of the degree of association between two binary variables, and represents the correlation between two dichotomous variables. It is based on adjusting chi-square significance to factor out sample size, and is the same as the Pearson correlation for two dichotomous variables. • Cramer’s V — Cramer's V is used to examine the association between two categorical variables when there is more than a 2 X 2 contingency (e.g., 2 X 3). In these more complex designs, phi is not appropriate, but Cramer's statistic is. Cramer's V represents the association or correlation between two variables. Cramer's V is the most popular of the chi-square-based measures of nominal association, designed so that the attainable upper limit is always 1. • Likelihood Ratio Chi Square — Likelihood ratio chi-square is an alternative to test the hypothesis of no association of columns and rows in nominal-level tabular data. It is based on maximum likelihood estimation, and involves the ratio between the observed and the expected frequencies, whereas the ordinary chi-square test involves the difference between the two. This is a more recent version of chi-square and is directly related to loglinear analysis and logistic regression. • Continuity-Adjusted Chi-Square — The continuity-adjusted chi-square statistic for 2 × 2 tables is similar to the Pearson chi-square, except that it is adjusted for the continuity of Teradata Warehouse Miner User Guide - Volume 1 329 Chapter 3: Statistical Tests Tests Based on Contingency Tables the chi-square distribution. The continuity-adjusted chi-square is most useful for small sample sizes. The use of the continuity adjustment is controversial; this chi-square test is more conservative, and more like Fisher's exact test, when your sample size is small. As the sample size increases, the statistic becomes more and more like the Pearson chisquare. • Contingency Coefficient — The contingency coefficient is an adjustment to phi coefficient, intended for tables larger than 2-by-2. It is always less than 1 and approaches 1.0 only for large tables. The larger the contingency coefficient, the stronger the association. Recommended only for 5-by-5 tables or larger, for smaller tables it underestimates level of association. Initiate a Chi Square Test Use the following procedure to initiate a new Chi Square Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 238: Add New Analysis from toolbar 2 330 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Tests Based on Contingency Tables: Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Tests Based on Contingency Tables Figure 239: Add New Analysis > Statistical Tests > Tests Based on Contingency Tables 3 This will bring up the Tests Based on Contingency Tables dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Chi Square Test - INPUT - Data Selection On the Tests Based on Contingency Tables dialog click on INPUT and then click on data selection: Figure 240: Chi Square Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis Teradata Warehouse Miner User Guide - Volume 1 331 Chapter 3: Statistical Tests Tests Based on Contingency Tables that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests Based on Contingency Tables available (Chi Square, Median). Select “Chi Square”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. • First Columns/Second Columns — Note that the Selected Columns window is actually a split window; you can insert columns as First Columns, Second Columns. Make sure you have the correct portion of the window highlighted. • First Columns — The set of columns that specifies the first of a pair of variables for Chi Square analysis. • Second Columns — The set of columns that specifies the second of a pair of variables for Chi Square analysis. Each combination of the first and second variables will generate a separate Chi Square test. (Limitation: to avoid excessively long execution, the number of combinations is limited to 100, and unless the product of the number of distinct values of each pair is 2000 or less, the calculation will be skipped.) Note: Group-By Columns are not available in the Chi Square Test. Chi Square Test - INPUT - Analysis Parameters On the Tests Based on Contingency Tables dialog click on INPUT and then click on analysis parameters: Figure 241: Chi Square Test > Input > Analysis Parameters On this screen enter or select: • Processing Options 332 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Tests Based on Contingency Tables • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. Chi Square Test - OUTPUT On the Tests Based on Contingency Tables dialog click on OUTPUT: Figure 242: Chi Square Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Teradata Warehouse Miner User Guide - Volume 1 333 Chapter 3: Statistical Tests Tests Based on Contingency Tables Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the Chi Square Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Chi Square Analysis The results of running the Chi Square Test analysis include a table with a row for each separate Chi Square test on all pairs of selected variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Chi Square Test - RESULTS - SQL On the Tests Based on Contingency Tables dialog click on RESULTS and then click on SQL: Figure 243: Chi Square Test > Results > SQL The series of SQL statements comprise the Chi Square Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Chi Square Test - RESULTS - data On the Tests Based on Contingency Tables dialog click on RESULTS and then click on data: Figure 244: Chi Square Test > Results > data The output table is generated by the Analysis for each separate Chi Square test on all pairs of selected variables 334 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Tests Based on Contingency Tables Output Columns - Chi Square Test Analysis The following table is built in the requested Output Database by the Chi Square test analysis. Column1 will be the Unique Primary Index (UPI). Table 107: Chi Square Test Analysis: Output Columns Name Type Definition column1 Char First of pair of variables column2 Char Second of pair of variables Chisq Float Chi Square Value DF INTEGER Degrees of Freedom Z Float Z Score CramersV Float § Cramer’s V PhiCoeff Float § Phi coefficient LlhChiSq Float Likelihood Ratio Chi Square ContAdjChiSq Float § Continuity-Adjusted Chi-Square ContinCoeff Float § Contingency Coefficient ChiPValue Float The probability associated with the Chi Square statistic ChiPText Char Text description if P is outside table range ChiCallP_0.05 Char The Chi Square result: a=accept, p=reject (positive), n=reject(negative) Tutorial - Chi Square Test Analysis In this example, a Chi Square test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Chi Square Test analysis as follows: • Available Tables — twm_customer_analysis • First Columns — female, single • Second Columns — svacct, ccacct, ckacct • Analysis Parameters • Threshold Probability — 0.05 Run the analysis and click on Results when it completes. For this example, the Chi Square Test analysis generated the following table. The Chi Square Test was computed on all combinations of pairs of the two sets of variables. Results were sorted by column1 and column2. The tests shows that probabilities observed are the same for three pairs of variables and different for three other pairs. A ‘p’ means significantly different and an ‘a’ means not significantly different. The SQL is available for viewing but not listed below. Teradata Warehouse Miner User Guide - Volume 1 335 Chapter 3: Statistical Tests Tests Based on Contingency Tables Table 108: Chi Square Test (Part 1) column1 column2 Chisq DF Z CramersV PhiCoeff LlhChiSq female ccacct 3.2131312 1 1.480358596 0.065584911 0.065584911 3.21543611 female ckacct 8.2389731 1 2.634555949 0.105021023 0.105021023 8.23745744 female svacct 3.9961257 1 1.716382791 0.073140727 0.073140727 3.98861957 single ccacct 6.9958187 1 2.407215881 0.096774063 0.096774063 7.01100739 single ckacct 0.6545145 1 0.191899245 0.02960052 0.02960052 0.65371179 single svacct 1.5387084 1 0.799100586 0.045385576 0.045385576 1.53297321 Table 109: Chi Square Test (Part 2) column1 column2 ContAdjChiSq ContinCoeff ChiPValue ChiPText female ccacct 2.954339388 0.065444311 0.077657185 a female ckacct 7.817638955 0.10444661 0.004512106 p female svacct 3.697357526 0.072945873 0.046729867 p single ccacct 6.600561728 0.096324066 0.00854992 p single ckacct 0.536617115 0.029587561 0.25 single svacct 1.35045989 0.045338905 0.226624385 >0.25 ChiCallP_0.05 a a Median Test The Median test is a special case of the chi-square test with fixed marginal totals. It tests whether several samples came from populations with the same median. The null hypothesis is that all samples have the same median. The median test is applied for data in similar cases as for the ANOVA for independent samples, but when: 1 the data are either importantly non-normally distributed 2 the measurement scale of the dependent variable is ordinal (not interval or ratio) 3 or the data sample is too small. Note: The Median test is a less powerful non-parametric test than alternative rank tests due to the fact the dependent variable is dichotomized at the median. Because this technique tends to discard most of the information inherent in the data, it is less often used. Frequencies are evaluated by a simple 2 x 2 contingency table, so it becomes simply a 2 x 2 chi square test of independence with 1 DF. Given k independent samples of numeric values, a Median test is produced for each set of unique values of the group-by variables (GBV's), if any, testing whether all the populations have the same median. Output for each set of unique values of the GBV's is a p-value, which 336 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Tests Based on Contingency Tables when compared to the user’s threshold, determines whether the null hypothesis should be rejected for the unique set of values of the GBV's. For more than 2 samples, this is sometimes called the Brown-Mood test. Initiate a Median Test Use the following procedure to initiate a new Median Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 245: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Tests Based on Contingency Tables: Figure 246: Add New Analysis > Statistical Tests > Tests Based On Contingency Tables 3 This will bring up the Tests Based on Contingency Tables dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Teradata Warehouse Miner User Guide - Volume 1 337 Chapter 3: Statistical Tests Tests Based on Contingency Tables Median Test - INPUT - Data Selection On the Tests Based on Contingency Tables dialog click on INPUT and then click on data selection: Figure 247: Median Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests Based on Contingency Tables available (Chi Square, Median). Select “Median”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Columns and Group By Columns. Make sure you have the correct portion of the window highlighted. 338 • Column of Interest — The numeric dependent variable for Median analysis. • Columns — The set of categorical independent variables for Median analysis. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Tests Based on Contingency Tables • Group By Columns — The column(s) that specifies the variable(s) whose distinct value combinations will categorize the data, so a separate test is performed on each category. Median Test - INPUT - Analysis Parameters On the Tests Based on Contingency Tables dialog click on INPUT and then click on analysis parameters: Figure 248: Median Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. Median Test - OUTPUT On the Tests Based on Contingency Tables dialog click on OUTPUT: Figure 249: Median Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). Teradata Warehouse Miner User Guide - Volume 1 339 Chapter 3: Statistical Tests Tests Based on Contingency Tables • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the Median Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Median Analysis The results of running the Median Test analysis include a table with a row for each separate Median test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Median Test - RESULTS - SQL On the Tests Based on Contingency Tables dialog click on RESULTS and then click on SQL: Figure 250: Median Test > Results > SQL 340 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Tests Based on Contingency Tables The series of SQL statements comprise the Median Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Median Test - RESULTS - data On the Tests Based on Contingency Tables dialog click on RESULTS and then click on data: Figure 251: Median Test > Results > data The output table is generated by the Analysis for each group-by variable combination. Output Columns - Median Test Analysis The following table is built in the requested Output Database by the Median Test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise ChiSq will be the UPI. Table 110: Median Test Analysis: Output Columns Name Type Definition Chisq Float Chi Square Value DF INTEGER Degrees of Freedom MedianPValue Float The probability associated with the Chi Square statistic MedianPText Char Text description if P is outside table range MedianCallP_0.01 Char The Chi Square result: a=accept, p=reject (positive), n=reject(negative) Tutorial - Median Test Analysis In this example, a Median test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Median Test analysis as follows: • Available Tables — twm_customer • Column of Interest — income • Columns — marital_status • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.01 Run the analysis and click on Results when it completes. For this example, the Median Test analysis generated the following table. The Median Test was computed on income over marital_status by years_with_bank. Teradata Warehouse Miner User Guide - Volume 1 341 Chapter 3: Statistical Tests Rank Tests Results were sorted by years_with_bank. The tests shows that values came from populations with the same median where MedianCallP_0.01 = ‘a’ (accept null hypothesis) and from populations with different medians where it is ‘p’ (reject null hypothesis). The SQL is available for viewing but not listed below. Table 111: Median Test years_with_bank ChiSq DF MedianPValue MedianPText MedianCallP_0.01 0 12.13288563 3 0.007361344 p 1 12.96799683 3 0.004848392 p 2 13.12480388 3 0.004665414 p 3 8.504645761 3 0.038753824 a 4 4.458333333 3 0.225502846 a 5 15.81395349 3 0.001527445 p 6 4.531466733 3 0.220383974 a 7 11.35971787 3 0.009950322 p 8 2.855999742 3 0.25 >0.25 a 9 2.23340311 3 0.25 >0.25 a Rank Tests Tests Based on Ranks use the ranks of the data rather than the data itself to calculate statistics. Therefore the data must have at least an ordinal scale of measurement. If data are nonnumeric but ordinal and ranked, these rank tests may be the most powerful tests available. Even numeric variables which meet the requirements of parametric tests, such as independent, randomly distributed normal variables, can be efficiently analyzed by these tests. These rank tests are valid for variables which are continuous, discrete, or a mixture of both. Types of Rank tests supported by Teradata Warehouse Miner include: • Mann-Whitney/Kruskal-Wallis • Mann-Whitney/Kruskal-Wallis (Independent Tests) • Wilcoxon Signed Rank • Friedman Mann-Whitney/Kruskal-Wallis Test The selection of which test to execute is automatically based on the number of distinct values of the independent variable. The Mann-Whitney is used for two groups, the Kruskal-Wallis for three or more groups. 342 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests A special version of the Mann-Whitney/Kruskal-Wallis test performs a separate, independent test for each independent variable, and displays the result of each test with its accompanying column name. Under the primary version of the Mann-Whitney/Kruskal-Wallis test, all independent variable value combinations are used, often forcing the Kruskal-Wallis test, since the number of value combinations exceeds two. When a variable which has more than two distinct values is included in the set of independent variables, then the Kruskal-Wallis test is performed for all variables. Since Kruskal-Wallis is a generalization of Mann-Whitney, the Kruskal-Wallis results are valid for all the variables, including two-valued ones. In the discussion below, both types of Mann-Whitney/Kruskal-Wallis are referred to as MannWhitney/Kruskal-Wallis tests, since the only difference is the way the independent variable is treated. The Mann-Whitney test, AKA Wilcoxon Two Sample Test, is the nonparametric analog of the 2-sample t test. It is used to compare two independent groups of sampled data, and tests whether they are from the same population or from different populations, i.e. whether the samples have the same distribution function. Unlike the parametric t-test, this non-parametric test makes no assumptions about the distribution of the data (e.g., normality). It is to be used as an alternative to the independent group t-test, when the assumption of normality or equality of variance is not met. Like many non-parametric tests, it uses the ranks of the data rather than the data itself to calculate the U statistic. But since the Mann-Whitney test makes no distribution assumption, it is less powerful than the t-test. On the other hand, the MannWhitney is more powerful than the t-test when parametric assumptions are not met. Another advantage is that it will provide the same results under any monotonic transformation of the data so the results of the test are more generalizable. The Mann-Whitney is used when the independent variable is nominal or ordinal and the dependent variable is ordinal (or treated as ordinal). The main assumption is that the variable on which the 2 groups are to be compared is continuously distributed. This variable may be non-numeric, and if so, is converted to a rank based on alphanumeric precedence. The null hypothesis is that both samples have the same distribution. The alternative hypotheses are that the distributions differ from each other in either direction (two-tailed test), or in a specific direction (upper-tailed or lower-tailed tests). Output is a p-value, which when compared to the user’s threshold, determines whether the null hypothesis should be rejected. Given one or more columns (independent variables) whose values define two independent groups of sampled data, and a column (dependent variable) whose distribution is of interest from the same input table, the Mann-Whitney test is performed for each set of unique values of the group-by variables (GBV's), if any. The Kruskal-Wallis test is the nonparametric analog of the one-way analysis of variance or Ftest used to compare three or more independent groups of sampled data. When there are only two groups, it reduces to the Mann-Whitney test (above). The Kruskal-Wallis test tests whether multiple samples of data are from the same population or from different populations, i.e. whether the samples have the same distribution function. Unlike the parametric independent group ANOVA (one way ANOVA), this non-parametric test makes no assumptions about the distribution of the data (e.g., normality). Since this test does not make a distributional assumption, it is not as powerful as ANOVA. Teradata Warehouse Miner User Guide - Volume 1 343 Chapter 3: Statistical Tests Rank Tests Given k independent samples of numeric values, a Kruskal-Wallis test is produced for each set of unique values of the GBV's, testing whether all the populations are identical. This test variable may be non-numeric, and if so, is converted to a rank based on alphanumeric precedence. The null hypothesis is that all samples have the same distribution. The alternative hypotheses are that the distributions differ from each other. Output for each unique set of values of the GBV's is a statistic H, and a p-value, which when compared to the user’s threshold, determines whether the null hypothesis should be rejected for the unique set of values of the GBV's. Initiate a Mann-Whitney/Kruskal-Wallis Test Use the following procedure to initiate a new Mann-Whitney/Kruskal-Wallis Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 252: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Rank Tests: Figure 253: Add New Analysis > Statistical Tests > Rank Tests 344 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests 3 This will bring up the Rank Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Mann-Whitney/Kruskal-Wallis Test - INPUT - Data Selection On the Ranks Tests dialog click on INPUT and then click on data selection: Figure 254: Mann-Whitney/Kruskal-Wallis Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests Based on Ranks available (Mann-Whitney/Kruskal-Wallis, MannWhitney/Kruskal-Wallis Independent Tests, Wilcoxon, Friedman). Select “MannWhitney/Kruskal-Wallis” or Mann-Whitney/Kruskal-Wallis Independent Tests. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Teradata Warehouse Miner User Guide - Volume 1 345 Chapter 3: Statistical Tests Rank Tests Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Columns or Group By Columns. Make sure you have the correct portion of the window highlighted. • Column of Interest — The column that specifies the dependent variable to be tested. Note that this variable may be non-numeric, but if so, will be converted to a rank based on alphanumeric precedence. • Columns — The columns that specify the independent variables, categorizing the data. • Group By Columns — The columns which specify the variables whose distinct value combinations will categorize the data, so a separate test is performed on each category. Mann-Whitney/Kruskal-Wallis Test - INPUT - Analysis Parameters On the Rank Tests dialog click on INPUT and then click on analysis parameters: Figure 255: Mann-Whitney/Kruskal-Wallis Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. • Single Tail — Select the box if single tailed test is desired (default is two-tailed). The single-tail option is only valid if the test is Mann-Whitney. Mann-Whitney/Kruskal-Wallis Test - OUTPUT On the Rank Tests dialog click on OUTPUT: Figure 256: Mann-Whitney/Kruskal-Wallis Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: • 346 Database Name — The database where the output table will be saved. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the Mann-Whitney/Kruskal-Wallis Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Mann-Whitney/Kruskal-Wallis Test Analysis The results of running the Mann-Whitney/Kruskal-Wallis Test analysis include a table with a row for each separate Mann-Whitney/Kruskal-Wallis test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. In the case of Mann-Whitney/ Teradata Warehouse Miner User Guide - Volume 1 347 Chapter 3: Statistical Tests Rank Tests Kruskal-Wallis Independent Tests, the results will be displayed with a separate row for each independent variable column-name. All of these results are outlined below. Mann-Whitney/Kruskal-Wallis Test - RESULTS - SQL On the Rank Tests dialog click on RESULTS and then click on SQL: Figure 257: Mann-Whitney/Kruskal-Wallis Test > Results > SQL The series of SQL statements comprise the Mann-Whitney/Kruskal-Wallis Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Mann-Whitney/Kruskal-Wallis Test - RESULTS - data On the Rank Tests dialog click on RESULTS and then click on data: Figure 258: Mann-Whitney/Kruskal-Wallis Test > Results > data The output table is generated by the Analysis for each separate Mann-Whitney/KruskalWallis test on all distinct-value group-by variables. Output Columns - Mann-Whitney/Kruskal-Wallis Test Analysis The following table is built in the requested Output Database by the Mann-Whitney/KruskalWallis test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise Z will be the UPI. In the case of Mann-Whitney/Kruskal-Wallis Independent Tests, the additional column _twm_independent_variable will contain the column-name of the independent variable for each separate test. Table for Mann-Whitney (if two groups) Table 112: Table for Mann-Whitney (if two groups) Name Type Definition Z Float Mann-Whitney Z Value 348 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests Table 112: Table for Mann-Whitney (if two groups) Name Type Definition MannWhitneyPValue Float The probability associated with the Mann-Whitney/Kruskal-Wallis statistic MannWhitneyCallP_0.01 Char The Mann-Whitney/Kruskal-Wallis result: a=accept, p=reject Table 113: Table for Kruskal-Wallis (if more than two groups) Name Type Definition Z Float Kruskal-Wallis Z Value ChiSq Float Kruskal-Wallis Chi Square Statistic DF Integer Degrees of Freedom KruskalWallisPValue Float The probability associated with the Kruskal-Wallis statistic KruskalWallisPText Char The text description of probability if out of table range KruskalWallisCallP_0.01 Char The Kruskal-Wallis result: a=accept, p=reject Tutorial 1 - Mann-Whitney Test Analysis In this example, a Mann-Whitney test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Mann-Whitney Test analysis as follows: • Available Tables — twm_customer • Column of Interest — income • Columns — gender (2 distinct values -> Mann-Whitney test) • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.01 • Single Tail — false (default) Run the analysis and click on Results when it completes. For this example, the MannWhitney Test analysis generated the following table. The Mann-Whitney Test was computed for each distinct value of the group by variable “years_with_bank”. Results were sorted by years_with_bank. The tests show that customer incomes by gender were from the same population for all values of years_with_bank (an ‘a’ means accept the null hypothesis). The SQL is available for viewing but not listed below. Table 114: Mann-Whitney Test years_with_bank Z MannWhitneyPValue MannWhitneyCallP_0.01 0 -0.0127 0.9896 a 1 -0.2960 0.7672 a Teradata Warehouse Miner User Guide - Volume 1 349 Chapter 3: Statistical Tests Rank Tests Table 114: Mann-Whitney Test years_with_bank Z MannWhitneyPValue MannWhitneyCallP_0.01 2 -0.4128 0.6796 a 3 -0.6970 0.4858 a 4 -1.8088 0.0705 a 5 -2.2541 0.0242 a 6 -0.8683 0.3854 a 7 -1.7074 0.0878 a 8 -0.8617 0.3887 a 9 -0.4997 0.6171 a Tutorial 2 - Kruskal-Wallis Test Analysis In this example, a Kruskal-Wallis test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Kruskal-Wallis Test analysis as follows: • Available Tables — twm_customer • Column of Interest — income • Columns — marital_status (4 distinct values -> Kruskal-Wallis test) • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.01 • Single Tail — false (default) Run the analysis and click on Results when it completes. For this example, the Kruskal-Wallis Test analysis generated the following table. The test was computed for each distinct value of the group by variable “years_with_bank”. Results were sorted by years_with_bank. The tests shows customer incomes by marital_status were from the same population for years_with_ bank 4, 6, 8 and 9. Those with years_with_bank 0-3, 5 and 7 were from different populations for each marital status. An ‘n’ or ‘p’ means significant and an ‘a’ means accept the null hypothesis. The SQL is available for viewing but not listed below. Table 115: Kruskal-Wallis Test years_with_bank Z ChiSq DF KruskalWallisPValue 0 3.5507 20.3276 3 0.0002 1 4.0049 24.5773 3 0.0001 2 3.3103 18.2916 3 0.0004 p 3 3.0994 16.6210 3 0.0009 p 4 1.5879 7.5146 3 0.0596 a 350 KruskalWallisPText KruskalWallisCallP_0.01 p <0.0001 p Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests Table 115: Kruskal-Wallis Test years_with_bank Z ChiSq DF KruskalWallisPValue KruskalWallisPText KruskalWallisCallP_0.01 5 4.3667 28.3576 3 0.0001 <0.0001 p 6 2.1239 10.2056 3 0.0186 a 7 3.2482 17.7883 3 0.0005 p 8 0.1146 2.6303 3 0.25 >0.25 a 9 -0.1692 2.0436 3 0.25 >0.25 a Tutorial 3 - Mann-Whitney Independent Tests Analysis In this example, a Mann-Whitney Independent Tests analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Mann-Whitney Independent Tests analysis as follows: • Available Tables — twm_customer_analysis • Column of Interest — income • Columns — gender, ccacct, ckacct, svacct • Group By Columns • Analysis Parameters • Threshold Probability — 0.05 • Single Tail — false (default) Run the analysis and click on Results when it completes. For this example, the MannWhitney Independent Tests analysis generated the following table. The Mann-Whitney Test was computed separately for each independent variable. The tests show that customer incomes by gender and by svacct were from different populations, and that customer incomes by ckacct and by ccacct were from identical populations. The SQL is available for viewing but not listed below. Table 116: Mann-Whitney Test _twm_independent Z MannWhitneyPValue MannWhitneyCallP_0.05 gender -3.00331351 0.002673462 n svacct -3.37298401 0.000743646 n ckacct -1.92490664 0.05422922 a ccacct 1.764991014 0.077563672 a Wilcoxon Signed Ranks Test The Wilcoxon Signed Ranks Test is an alternative analogous to the t-test for correlated samples. The correlated-samples t-test makes assumptions about the data, and can be properly applied only if certain assumptions are met: Teradata Warehouse Miner User Guide - Volume 1 351 Chapter 3: Statistical Tests Rank Tests 1 the scale of measurement has the properties of an equal-interval scale 2 differences between paired values are randomly selected from the source population 3 The source population has a normal distribution. If any of these assumptions are invalid, the t-test for correlated samples should not be used. Of cases where these assumptions are unmet, the most common are those where the scale of measurement fails to have equal-interval scale properties, e.g. a case in which the measures are from a rating scale. When data within two correlated samples fail to meet one or another of the assumptions of the t-test, an appropriate non-parametric alternative is the Wilcoxon Signed-Rank Test, a test based on ranks. Assumptions for this test are: 1 The distribution of difference scores is symmetric (implies equal interval scale) 2 difference scores are mutually independent 3 difference scores have the same mean The original measures are replaced with ranks resulting in analysis only of the ordinal relationships. The signed ranks are organized and summed, giving a number, W. When the numbers of positive and negative signs are about equal, i.e. there is no tendency in either direction, the value of W will be near zero, and the null hypothesis will be supported. Positive or negative sums indicate there is a tendency for the ranks to have significance so there is a difference in the cases in the specified direction. Given a table name and names of paired numeric columns, a Wilcoxon test is produced. The Wilcoxon tests whether a sample comes from a population with a specific mean or median. The null hypothesis is that the samples come from populations with the same mean or median. The alternative hypothesis is that the samples come from populations with different means or medians (two-tailed test), or that in addition the difference is in a specific direction (upper-tailed or lower-tailed tests). Output is a p-value, which when compared to the user’s threshold, determines whether the null hypothesis should be rejected. Initiate a Wilcoxon Signed Ranks Test Use the following procedure to initiate a new Wilcoxon Signed Ranks Test in Teradata Warehouse Miner: 1 Click on the Add New Analysis icon in the toolbar: Figure 259: Add New Analysis from toolbar 2 352 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Rank Tests: Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests Figure 260: Add New Analysis > Statistical Tests > Rank Tests 3 This will bring up the Rank Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Wilcoxon Signed Ranks Test - INPUT - Data Selection On the Rank Tests dialog click on INPUT and then click on data selection: Figure 261: Wilcoxon Signed Ranks Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis Teradata Warehouse Miner User Guide - Volume 1 353 Chapter 3: Statistical Tests Rank Tests that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests Based on Ranks available (Mann-Whitney/Kruskal-Wallis, Wilcoxon, Friedman). Select “Wilcoxon”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as First Column, Second Column, Group By Columns. Make sure you have the correct portion of the window highlighted. • First Column — The column that specifies the variable from the first sample • Second Column — The column that specifies the variable from the second sample • Group By Columns — The columns which specify the variables whose distinct value combinations will categorize the data, so a separate test is performed on each category. Wilcoxon Signed Ranks Test - INPUT - Analysis Parameters On the Rank Tests dialog click on INPUT and then click on analysis parameters: Figure 262: Wilcoxon Signed Ranks Test > Input > Analysis Parameters On this screen enter or select: • Processing Options 354 • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. • Single Tail — Select the box if single tailed test is desired (default is two-tailed). The single-tail option is only valid if the test is Mann-Whitney. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests • Include Zero — The “include zero” option generates a variant of the Wilcoxon in which zero differences are included with the positive count. The default “discard zero” option is the true Wilcoxon. Wilcoxon Signed Ranks Test - OUTPUT On the Rank Tests dialog click on OUTPUT: Figure 263: Wilcoxon Signed Ranks Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). Teradata Warehouse Miner User Guide - Volume 1 355 Chapter 3: Statistical Tests Rank Tests • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the Wilcoxon Signed Ranks Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Wilcoxon Analysis The results of running the Wilcoxon Signed Ranks Test analysis include a table with a row for each separate Wilcoxon Signed Ranks Test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Wilcoxon Signed Ranks Test - RESULTS - SQL On the Rank Tests dialog click on RESULTS and then click on SQL: Figure 264: Wilcoxon Signed Ranks Test > Results > SQL The series of SQL statements comprise the Wilcoxon Signed Ranks Test Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Wilcoxon Signed Ranks Test - RESULTS - data On the Rank Tests dialog click on RESULTS and then click on data: Figure 265: Wilcoxon Signed Ranks Test > Results > data The output table is generated by the Analysis for each separate Wilcoxon Signed Ranks Test on all distinct-value group-by variables. 356 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests Output Columns - Wilcoxon Signed Ranks Test Analysis The following table is built in the requested Output Database by the Wilcoxon Signed Ranks Test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise Z_ will be the UPI. Table 117: Wilcoxon Signed Ranks Test Analysis: Output Columns Name Type Definition N Integer variable count Z_ Float Mann-Whitney Z Value WilcoxonPValue Float The probability associated with the Wilcoxon statistic WilcoxonCallP_0.05 Char The Wilcoxon result: a=accept, p or n=reject Tutorial - Wilcoxon Test Analysis In this example, a Wilcoxon test analysis is performed on the fictitious banking data to analyze account usage. Parameterize a Wilcoxon Test analysis as follows: • Available Tables — twm_customer_analysis • First Column — avg_ck_bal • Second Column — avg_sv_bal • Group By Columns — years_with_bank • Analysis Parameters • Threshold Probability — 0.05 • Single Tail — false (default) • Include Zero — false (default) Run the analysis and click on Results when it completes. For this example, the Wilcoxon Test analysis generated the following table. The Wilcoxon Test was computed for each distinct value of the group by variable “gender”. The tests show the samples of avg_ck_bal and avg_ sv_bal came from populations with the same mean or median for customers with years_with_ bank of 0, 4-9, and from populations with different means or medians for those with years_ with_bank of 1-3. An ‘n’ or ‘p’ means significant and an ‘a’ means accept the null hypothesis. The SQL is available for viewing but not listed below. Table 118: Wilcoxon Test years_with_bank N Z_ WilcoxonPValue WilcoxonCallP_0.05 0 75 -1.77163 0.07639 a 1 77 -3.52884 0.00042 n 2 83 -2.94428 0.00324 n 3 69 -2.03882 0.04145 n Teradata Warehouse Miner User Guide - Volume 1 357 Chapter 3: Statistical Tests Rank Tests Table 118: Wilcoxon Test years_with_bank N Z_ WilcoxonPValue WilcoxonCallP_0.05 4 69 -0.56202 0.57412 a 5 67 -1.95832 0.05023 a 6 65 -1.25471 0.20948 a 7 48 -0.44103 0.65921 a 8 39 -1.73042 0.08363 a 9 33 -1.45623 0.14539 a Friedman Test with Kendall's Coefficient of Concordance & Spearman's Rho The Friedman test is an extension of the sign test for several independent samples. It is analogous to the 2-way Analysis of Variance, but depends only on the ranks of the observations, so it is like a 2-way ANOVA on ranks. The Friedman test should not be used for only three treatments due to lack of power, and is best for six or more treatments. It is a test for treatment differences in a randomized, complete block design. Data consists of b mutually independent k-variate random variables called blocks. The Friedman assumptions are that the data in these blocks are mutually independent, and that within each block, observations are ordinally rankable according to some criterion of interest. A Friedman Test is produced using rank scores and the F table, though alternative implementations call it the Friedman Statistic and use the chi-square table. Note that when all of the treatments are not applied to each block, it is an incomplete block design. The requirements of the Friedman test are not met under these conditions, and other tests such as the Durban test should be applied. In addition to the Friedman statistics, Kendall’s Coefficient of Concordance (W) is produced, as well as Spearman’s Rho. Kendall's coefficient of concordance can range from 0 to 1. The higher its value, the stronger the association. W is 1.0 if all treatments receive the same rankness in all blocks, and 0 if there is “perfect disagreement” among blocks. Spearman's rho is a measure of the linear relationship between two variables. It differs from Pearson's correlation only in that the computations are done after the numbers are converted to ranks. Spearman’s Rho equals 1 if there is perfect agreement among rankings; disagreement causes rho to be less than 1, sometimes becoming negative. Initiate a Friedman Test Use the following procedure to initiate a new Friedman Test in Teradata Warehouse Miner: 358 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests 1 Click on the Add New Analysis icon in the toolbar: Figure 266: Add New Analysis from toolbar 2 In the resulting Add New Analysis dialog box, click on Statistical Tests under Categories and then under Analyses double-click on Rank Tests: Figure 267: Add New Analysis > Statistical Tests > Rank Tests 3 This will bring up the Rank Tests dialog in which you will enter STATISTICAL TEST STYLE, INPUT and OUTPUT options to parameterize the analysis as described in the following sections. Friedman Test - INPUT - Data Selection On the Rank Tests dialog click on INPUT and then click on data selection: Teradata Warehouse Miner User Guide - Volume 1 359 Chapter 3: Statistical Tests Rank Tests Figure 268: Friedman Test > Input > Data Selection On this screen select: 1 Select Input Source Users may select between different sources of input. By selecting the Input Source Table the user can select from available databases, tables (or views) and columns in the usual manner. By selecting the Input Source Analysis however the user can select directly from the output of another analysis of qualifying type in the current project. Analyses that may be selected from directly include all of the Analytic Data Set (ADS) and Reorganization analyses (except Refresh). In place of Available Databases the user may select from Available Analyses, while Available Tables then contains a list of all the output tables that will eventually be produced by the selected Analysis, or it contains a single entry with the name of the analysis under the label Volatile Table, representing the output of the analysis that is ordinarily produced by a Select statement. For more information, refer to “INPUT Tab” on page 73 of the Teradata Warehouse Miner User Guide (Volume 1). 2 3 Select Columns From a Single Table • Available Databases (or Analyses) — These are the databases (or analyses) available to be processed. • Available Tables — These are the tables and views that are available to be processed. • Available Columns — These are the columns within the table/view that are available for processing. Select Statistical Test Style These are the Tests Based on Ranks available (Mann-Whitney/Kruskal-Wallis, Wilcoxon, Friedman). Select “Friedman”. 4 Select Optional Columns • Selected Columns — Select columns by highlighting and then either dragging and dropping into the Selected Columns window, or click on the arrow button to move highlighted columns into the Selected Columns window. Note: The Selected Columns window is actually a split window; you can insert columns as Column of Interest, Treatment Column, Block Column, Group By Columns. Make sure you have the correct portion of the window highlighted. 360 • Column of Interest — The column that specifies the dependent variable to be analyzed • Treatment Column — The column that specifies the independent categorical variable representing treatments within blocks. • Block Column — The column that specifies the variable representing blocks, or independent experimental groups. Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests Warning: Equal cell counts are required for all Treatment Column x Block Column pairs. Division by zero may occur in the case of unequal cell counts. • Group By Columns — The columns which specify the variables whose distinct value combinations will categorize the data, so a separate test is performed on each category. Warning: Equal cell counts are required for all Treatment Column x Block Column pairs within each group. Division by zero may occur in the case of unequal cell counts. Friedman Test - INPUT - Analysis Parameters On the Rank Tests dialog click on INPUT and then click on analysis parameters: Figure 269: Friedman Test > Input > Analysis Parameters On this screen enter or select: • Processing Options • Threshold Probability — Enter the “alpha” probability below which to reject the null hypothesis. Friedman Test - OUTPUT On the Rank Tests dialog click on OUTPUT: Figure 270: Friedman Test > Output On this screen select the following options if desired: • Store the tabular output of this analysis in the database — Option to generate a Teradata table populated with the results of the analysis. Once enabled, the following three fields must be specified: • Database Name — The database where the output table will be saved. • Output Name — The table name that the output will be saved under. • Output Type — The output type must be table when storing Statistical Test output in the database. • Stored Procedure — The creation of a stored procedure containing the SQL generated for this analysis can be requested by entering the desired name of the stored procedure here. This will result in the creation of a stored procedure in the user's login database Teradata Warehouse Miner User Guide - Volume 1 361 Chapter 3: Statistical Tests Rank Tests in place of the execution of the SQL generated by the analysis. (For more information, please refer to “Stored Procedure Support” on page 109 of the Teradata Warehouse Miner User Guide (Volume 1)). • Procedure Comment — When an optional Procedure Comment is entered it is applied to a requested Stored Procedure with an SQL Comment statement. It can be up to 255 characters in length and contain substitution parameters for the output category (Score, ADS, Stats or Other), project name and/or analysis name (using the tags <Category>, <Project> and <Analysis>, respectively). (Note that the default value of this field may be set on the Defaults tab of the Preferences dialog, available from the Tools Menu). • Create output table using fallback keyword — Fallback keyword will be used to create the table • Create output table using multiset keyword — Multiset keyword will be used to create the table • Advertise Output — The Advertise Output option may be requested when creating a table, view or procedure. This feature “advertises” output by inserting information into one or more of the Advertise Output metadata tables according to the type of analysis and the options selected in the analysis. (For more information, refer to “Advertise Output” on page 112 of the Teradata Warehouse Miner User Guide (Volume 1)). • Advertise Note — An Advertise Note may be specified if desired when the Advertise Output option is selected or when the Always Advertise option is selected on the Databases tab of the Connection Properties dialog. It is a free-form text field of up to 30 characters that may be used to categorize or describe the output. • Generate SQL, but do not Execute it — Generate the Statistical Test SQL, but do not execute it. The SQL will be available to be viewed. Run the Friedman Test Analysis After setting parameters on the INPUT screens as described above, you are ready to run the analysis. To run the analysis you can either: • Click the Run icon on the toolbar, or • Select Run <project name> on the Project menu, or • Press the F5 key on your keyboard Results - Friedman Test Analysis The results of running the Friedman Test analysis include a table with a row for each separate Friedman Test on all distinct-value group-by variables, as well as the SQL to perform the statistical analysis. All of these results are outlined below. Friedman Test - RESULTS - SQL On the Rank Tests dialog click on RESULTS and then click on SQL: 362 Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests Figure 271: Friedman Test > Results > SQL The series of SQL statements comprise the Analysis. It is always returned, and is the only item returned when the Generate SQL without Executing option is used. Friedman Test - RESULTS - data On the Rank Tests dialog click on RESULTS and then click on data: Figure 272: Friedman Test > Results > data The output table is generated by the Analysis for each separate Friedman Test on all distinctvalue group-by variables. Output Columns - Friedman Test Analysis The following table is built in the requested Output Database by the Friedman Test analysis. Group By Variables, if present, will be the Unique Primary Index (UPI). Otherwise Kendalls_ W will be the UPI. Table 119: Friedman Test Analysis: Output Columns Name Type Definition Kendalls_W Float Kendall's W Average_Spearmans_Rho Float Average Spearman's Rho DF_1 Integer Degrees of Freedom for Treatments DF_2 Integer Degrees of Freedom for Blocks F Float 2-Way ANOVA F Statistic on ranks FriedmanPValue Float The probability associated with the Friedman statistic FriedmanPText Char The text description of probability if out of table range FriedmanCallP_0.05 Char The Friedman result: a=accept, p or n=reject Teradata Warehouse Miner User Guide - Volume 1 363 Chapter 3: Statistical Tests Rank Tests Tutorial - Friedman Test Analysis In this example, a Friedman test analysis is performed on the fictitious banking data to analyze account usage. If the data does not have equal cell counts in the treatment x block cells, stratified sampling can be used to identify the smallest count, and then produce a temporary table which can be analyzed. The first step is to identify the smallest count with a Free Form SQL analysis (or two Variable Creation analyses) with SQL such as the following (be sure to set the database in the FROM clause to that containing the demonstration data tables): SELECT MIN("_twm_N") AS smallest_count FROM ( SELECT marital_status ,gender ,COUNT(*) AS "_twm_N" FROM "twm_source"."twm_customer_analysis" GROUP BY "marital_status", "gender" ) AS "T0"; The second step is to use a Sample analysis with stratified sampling to create the temporary table with equal cell counts. The value 18 used in the stratified Sizes/Fractions parameter below corresponds to the smallest_count returned from above. Parameterize a Sample Analysis called Friedman Work Table Setup as follows: Input Options: • Available Tables — TWM_CUSTOMER_ANALYSIS • Selected Columns and Aliases • TWM_CUSTOMER_ANALYSIS.cust_id • TWM_CUSTOMER_ANALYSIS.gender • TWM_CUSTOMER_ANALYSIS.marital_status • TWM_CUSTOMER_ANALYSIS.income Analysis Parameters: • Sample Style — Stratified • Stratified Sample Options • Create a separate sample for each fraction/size — Enabled • Stratified Conditions 364 • gender='f' and marital_status='1' • gender='f' and marital_status='2' • gender='f' and marital_status='3' • gender='f' and marital_status='4' • gender='m' and marital_status='1' • gender='m' and marital_status='2' • gender='m' and marital_status='3' Teradata Warehouse Miner User Guide - Volume 1 Chapter 3: Statistical Tests Rank Tests • gender='m' and marital_status='4' • Sizes/Fractions — 18 (use the same value for all conditions) Output Options: • Store the tabular output of this analysis in the database — Enabled • Table Name — Twm_Friedman_Worktable Finally, Parameterize a Friedman Test analysis as follows: Input Options: • Select Input Source — Analysis • Available Analyses — Friedman Work Table Setup • Available Tables — Twm_Friedman_Worktable • Select Statistical Test Style — Friedman • Column of Interest — income • Treatment Column — gender • Block Column — marital_status Analysis Parameters: • Analysis Parameters • Threshold Probability — 0.05 Run the analysis and click on Results when it completes. For this example, the Friedman Test analysis generated the following table. (Note that results may vary due to the use of sampling in creating the input table Twm_Friedman_Worktable). The test shows that analysis of income by treatment (male vs. female) differences is significant at better than the 0.001 probability level. An ‘n’ or ‘p’ means significant and an ‘a’ means accept the null hypothesis. The SQL is available for viewing but not listed below. Table 120: Friedman Test Kendalls_W Average_Spearmans_Rho DF_1 DF_2 F FriedmanPValue FriedmanPText FriedmanCallP_0.001 0.76319692 5 0.773946177 1 0.001 p Teradata Warehouse Miner User Guide - Volume 1 71 228.8271876 <0.001 365 Chapter 3: Statistical Tests Rank Tests 366 Teradata Warehouse Miner User Guide - Volume 1 APPENDIX A References 1 Agrawal, R. Mannila, H. Srikant, R. Toivonen, H. and Verkamo, I., Fast Discovery of Association Rules. In Advances in Knowledge Discovery and Data Mining, 1996, eds. U.M. Fayyad, G. Paitetsky-Shapiro, P. Smyth and R. Uthurusamy. Menlo Park, AAAI Press/The MIT Press. 2 Agresti, A. (1990) Categorical Data Analysis. Wiley, New York. 3 Arabie, P., Hubert, L., and DeSoete, G., Clustering and Classification, World Scientific, 1996 4 Belsley, D.A., Kuh, E., and Welsch, R.E. (1980) Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. Wiley, New York. 5 Bradley, P., Fayyad, U. and Reina, C., Scaling EM Clustering to Large Databases, Microsoft Research Technical Report MSR-TR-98-35, 1998 6 Breiman, L., Friedman, J.H., Olshen, R.A., and Stone, C.J. Classification and Regression Trees. Wadsworth, Belmont, 1984. 7 Conover, W.J. Practical Nonparametric Statistics 3rd Edition 8 Cox, D.R. and Hinkley, D.V. (1974) Theoretical Statistics. Chapman & Hall/CRC, New York. 9 D'Agostino, RB. (1971) An omnibus test of normality for moderate and large size samples, Biometrica, 58, 341-348 10 D'Agostino, R. B. and Stephens, M. A., eds. Goodness-of-fit Techniques, 1986,. New York: Dekker. 11 D’Agostino, R, Belanger, A., and D’Agostino,R. Jr., A Suggestion for Using Powerful and Informative Tests of Normality, American Statistician, 1990, Vol. 44, No. 4 12 Finn, J.D. (1974) A General Model for Multivariate Analysis. Holt, Rinehart and Winston, New York. 13 Harman, H.H. (1976) Modern Factor Analysis. University of Chicago Press, Chicago. 14 Harter, H.L. and Owen, D.B., eds, Selected Tables in Mathematical Statistics, Vol. 1.. Providence, Rhode Island: American Mathematical Society. 15 Hosmer, D.W. and Lemeshow, S. (1989) Applied Logistic Regression. Wiley, New York. 16 Jennrich, R.I., and Sampson, P.F. (1966) Rotation For Simple Loadings. Psychometrika, Vol. 31, No. 3. 17 Johnson, R.A. and Wichern, D.W. (1998) Applied Multivariate Statistical Analysis, 4th Edition. Prentice Hall, New Jersey. 18 Kachigan, S.K. (1991) Multivariate Statistical Analysis. Radius Press, New York. 19 Kaiser, Henry F. (1958) The Varimax Criterion For Analytic Rotation In Factor Analysis. Psychometrika, Vol. 23, No. 3. Teradata Warehouse Miner User Guide - Volume 3 367 Appendix A: References 20 Kass, G. V. (1979) An Exploratory Technique for Investigating Large Quantities of Categorical Data, Applied Statistics (1980) 29, No. 2 pp. 119-127 21 Kaufman, L. and Rousseeuw, P., Finding Groups in Data, J Wiley & Sons, 1990 22 Kennedy, W.J. and Gentle, J.E. (1980) Statistical Computing. Marcel Dekker, New York. 23 Kleinbaum, D.G. and Kupper, L.L. (1978) Applied Regression Analysis and Other Multivariable Methods. Duxbury Press, North Scituate, Massachusetts. 24 Maddala, G.S. (1983) Limited-Dependent and Qualitative Variables In Econometrics. Cambridge University Press, Cambridge, United Kingdom. 25 Maindonald, J.H. (1984) Statistical Computation. Wiley, New York. 26 McCullagh, P.M. and Nelder, J.A. (1989) Generalized Linear Models, 2nd Edition. Chapman & Hall/CRC, New York. 27 McLachlan, G.J. and Krishnan, T., The EM Algorithm and Extensions, J Wiley & Sons, 1997 28 Menard, S (1995) Applied Logistic Regression Analysis, Sage, Thousand Oaks 29 Mulaik, S.A. (1972) The Foundations of Factor Analysis. McGraw-Hill, New York. 30 Neter, J., Kutner, M.H., Nachtsheim, C.J., and Wasserman, W. (1996) Applied Linear Statistical Models, 4th Edition. WCB/McGraw-Hill, New York. 31 NIST/SEMATECH e-Handbook of Statistical Methods, http://www.itl.nist.gov/div898/ handbook/, 2005. 32 Nocedal, J. and Wright, S.J. (1999) Numerical Optimization. Springer-Verlag, New York. 33 Orchestrate/OSH Component User’s Guide Vol II, Analytics Library, Chapter 2: Introduction to Data Mining. Torrent Systems, Inc., 1997. 34 Ordonez, C. and Cereghini, P. (2000) SQLEM: Fast Clustering in SQL using the EM Algorithm. SIGMOD Conference 2000: 559-570 35 Ordonez, C. (2004): Programming the K-means clustering algorithm in SQL. KDD 2004: 823-828 36 Ordonez, C. (2004): Horizontal aggregations for building tabular data sets. DMKD 2004: 35-42 37 Pagano, Gauvreau Principles of Biostatistics 2nd Edition 38 Peduzzi, P.N., Hardy, R.J., and Holford, T.R. (1980) A Stepwise Variable Selection Procedure for Nonlinear Regression Models. Biometrics 36, 511-516. 39 Pregibon, D. (1981) Logistic Regression Diagnostics. Annals of Statistics, Vol. 9, No. 4, 705-724. 40 PROPHET StatGuide, BBN Corporation, 1996. 41 Quinlan, J.R. C4.5: Programs for Machine Learning. Morgan Kaufmann, San Mateo, 1993. 42 Roweis, S. and Ghahramani, Z., A Unifying Review of Linear Gaussian Models, Journal of Neural Computation, 1999 368 Teradata Warehouse Miner User Guide - Volume 3 Appendix A: References 43 Royston, JP., An Extension of Shapiro and Wilk’s W Test for Normality to Large Samples, Applied Statistics, 1982, 31, No. 2, pp.115-124 44 Royston, JP, Algorithm AS 177: Expected normal order statistics (exact and approximate), 1982, Applied Statistics, 31, 161-165. 45 Royston, JP., Algorithm AS 181: The W Test for Normality. 1982, Applied Statistics, 31, 176-180. 46 Royston , JP., A Remark on Algorithm AS 181: The W Test for Normality., 1995, Applied Statistics, 44, 547-551. 47 Rubin, Donald B., and Thayer, Dorothy T. (1982) EM Algorithms For ML Factor Analysis. Psychometrika, Vol. 47, No. 1. 48 Shapiro, SS and Francia, RS (1972). An approximate analysis of variance test for normality, Journal of the American Statistical Association, 67, 215-216 49 SPSS 7.5 Statistical Algorithms Manual, SPSS Inc., Chicago. 50 SYSTAT 9: Statistics I. (1999) SPSS Inc., Chicago. 51 Takahashi, T. (2005) Getting Started: International Character Sets and the Teradata Database, Teradata Corporation, 541-0004068-C02 52 Tatsuoka, M.M. (1971) Multivariate Analysis: Techniques For Educational and Psychological Research. Wiley, New York. 53 Tatsuoka, M.M. (1974) Selected Topics in Advanced Statistics, Classification Procedures, Institute for Personality and Ability Testing, 1974 54 Teradata Database SQL Functions, Operators, Expressions, and Predicates Release 14.10, B035-1145-112A, May 2013 55 Teradata Warehouse Miner Model Manager User Guide, B035-2303-093A, September 2013 56 Teradata Warehouse Miner Release Definition, B035-2494-093C, September 2013 57 Teradata Warehouse Miner User Guide, Volume 1 Introduction and Profiling, B035-2300- 093A, September 2013 58 Teradata Warehouse Miner User Guide, Volume 2 ADS Generation, B035-2301-093A, September 2013 59 Teradata Warehouse Miner User Guide, Volume 3 Analytic Functions, B035-2302-093A, September 2013 60 Teradata Warehouse Miner User’s Guide Release 03.00.02, B035-2093-022A, January 2002 61 Wendorf, Craig A., MANUALS FOR UNIVARIATE AND MULTIVARIATE STATISTICS © 1997, Revised 2004-03-12, UWSP, http://www.uwsp.edu/psych/cw/ statmanual, 2005 62 Wilkinson, L., Blank, G., and Gruber, C. (1996) Desktop Data Analysis SYSTAT. Prentice Hall, New Jersey. Teradata Warehouse Miner User Guide - Volume 3 369 Appendix A: References 370 Teradata Warehouse Miner User Guide - Volume 3