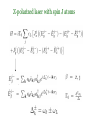Download Slides - Max-Planck

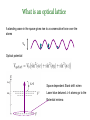
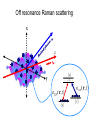
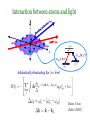
Detecting atoms in a lattice with two
photon raman transitions
Inés de Vega, Diego Porras, Ignacio Cirac
Max Planck Institute of Quantum Optics
Garching (Germany)
Summary
1) Motivation:
 what is an atom lattice?
 why measuring atoms in a lattice?
2) Measuring atoms in a lattice:
 Time of flight experiments
 Our method
3)
Conclusions
Richard Feynman, December 29th 1959 at the annual meeting of the
American Physical Society at the California Institute of Technology
(Caltech)
“I am not afraid to consider the final
question as to whether, ultimately---in
the great future---we can arrange the
atoms the way we want; the very atoms,
all the way down! “
Richard Feynman, December 29th 1959 at the annual meeting of the
American Physical Society at the California Institute of Technology
(Caltech)
What would the properties of materials be if we
could really arrange the atoms the way we want
them? […] I can't see exactly what would
happen, but I can hardly doubt that when we
have some control of the arrangement of things
on a small scale we will get an enormously
greater range of possible properties that
substances can have, and of different things
that we can do.
What is an optical lattice
A standing wave in the space gives rise to a conservative force over the
atoms
V0
Optical potential
What is an optical lattice
A standing wave in the space gives rise to a conservative force over the
atoms
V0
Optical potential
>0
Space dependent Stark shift: when
Laser blue detuned >0 atoms go to the
Potential minima
What is an optical lattice
Due to the periodic potential, the discrete levels in each well form Bloch
bands
We consider the atoms placed in the lowest Bloch band
Described with creation fuction of a particle of spin α:
Creation operator with bosonic
(fermionic) conmutation
(anticonmutation) relations
Wannier functions localiced in
each lattice site.
Atom Hamiltonian in second quantization
Gives rise to a kinetic term, with magnitude “t”
Gives rise to a repulsive term, with
magnitude ~ U.
Atom Hamiltonian in second quantization
Gives rise to a kinetic term, with magnitude “t”
Gives rise to a repulsive term, with
magnitude ~U.
Spin-spin
interactions
(example, for
atoms with J=1)
Atom Hamiltonian in second quantization
Gives rise to a kinetic term, with magnitude “t”
Gives rise to a repulsive term, with
magnitude ~U.
Variating parameters t and U, this hamiltonian undergoes Quantum Phase
Transitions
An optical lattice is controllable
We can change the standing wave parameters: V0 and λ
We can apply an external magnetic field to increase scattering length
We can use state dependent potentials
V0
λ
t>>U :Shallow lattice (large kinetic energy), gives rise to a superfluid state
T<<U :Deep lattice, strong interactions, gives rise to a Mott state. Atoms
are localized in each site.
Mott state very important:
1) To simulate magnetic Hamiltonians (spin-spin interactions)
2) As a quantum register (where highly entangled states, cluster states, can
be created)
Why measuring atoms in a lattice
A lattice is a nice quantum simulator, and may be a nice
implementation of a quantum computer but...
...how can we read out the information from it?
Time of flight experiments
Off-resonant Ramman
scattering of light
and more...
Time of flight
•S. Fölling et al.
Nature (2005)
•T. Rom et al.
Nature (2006)
Off resonance Raman scattering
x
z
y
Interaction between atoms and light
x
z
y
Adiabatically eliminating the e> level
Duan, Cirac,
Zoller (2002)
Z-polarized laser with spin J atoms
z
x
y
J’
We detect atoms with any spin J
J
Z-polarized laser with spin J atoms
Photon counting type of measure
Detected correlations of
photons
Correlations of atom
variables in momentum
space
x
k
z
y
  
k  k  k L
And if we consider T<<1/Γ we detect
atom correlations in the ground states
(1)
(2)
This is our main assumption.
We check the relative error between (1) and (2) with respect to the number of
photons that are emitted.
Checking the assumption T<<1/Γ
Through the Quantum Regression Theorem this is the evolution that
correlations have
q
1
L
Even if there were some lattice
sites without an atom, this function
for large L  3 N is approximately
a delta.
80
60
40
20
0.3
0.2
0.1
0.1
20
0.2
0.3
q
Checking the assumption T<<1/Γ
Number of y-polarized photons in
θ for T=0.0025
This is the type of
things we measure
15
Nyy () number of
photons detected
14
Nyy () number photons
comming from ground
state
13
0.5
1
1.5
2
Checking the assumption T<<1/Γ
J/B=0.001
J/B=-0.05
J/B=-0.5
Measuring conbinations of quadratures…
…we can detect any correlation!!
Conclusions
-Not destructive: one can perform measures of the
state in the middle of an experiment and then
continue
-More freedom to compute different correlations and
hence to detect more complex phases
-More precission with respect to time of flight:
Signal to noise ration in Time of flight
~ 1/ N
in Raman scattering~ N
-3D information
Thank You!!