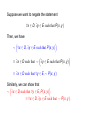Download Chapter 2: The Logic of Quantified Statements

Chapter 2: The Logic of Quantified
Statements
January 22, 2010
Outline
1 2.1- Introduction to Predicates and Quantified Statements I
2 2.2 - Introduction to Predicates and Quantified Statements II
3 2.3 - Statements Containing Multiple Quantifiers
2.1- Introduction to Predicates and Quantified Statements I
Basic Facts and Notation for Sets
• A set is some collection of objects, which we call elements of
the set.
For example,
A = { blue, red, yellow}
and
B = {0, 2, 5, 13, −4}
are examples of sets.
• To write the fact that an object x is an element of a set A, we
write x ∈ A
• x∈
/ A will denote the fact that x is not an element of A.
• We will use the following notation for familiar sets of numbers:
(1) R for the set of all real numbers
(2) Z for the set of all integers
(3) Q for the set of all rational numbers
(4) N for the set of all natural numbers
(i.e. positive integers)
• By putting + or − in the superscript, we indicate the set of
positive or negative numbers. For example, R+ denotes the set
of all positive real numbers.
Ex. “x + 4 > 9” is not a statement because its truth (or falsity)
depends on what value we assign to x.
Ex. If we do not define who “she” is, then
“She is a student at Ryerson” is technically not a statement.
• Such statements are called predicates. They are not
statements unless we interpret the variables in them as
particular elements of some prescribed set.
DEFINITION: A predicate is a sentence that contains a finite
number of variables and becomes a statement once these
variables are assigned specific values. The domain of a
predicate variable is the set of all values that can be substituted
for the variable.
• Suppose P(x) is the predicate “x + 4 > 9“ – the domain can
be any set of numbers (R, Z, . . . ,) in which its operations
(+, −, . . . ) make sense.
• A predicate could involve any number of variables, for
example Q(x, y) is the predicate x is divisible by y 3 .
DEFINITION: If P(x) is a predicate whose truth domain is D, the
truth set of P(x) is the set of all elements of D which make P(x)
true when they are substituted for x. We write the truth set for
P(x) as
{x ∈ D | P(x)}
which we read as “the set of all x in D such that P(x) is true”.
Ex. Let Q(n) be the predicate
n divides 5
If the truth domain is Z, then the truth set is {−5, −1, 1, 5}
If the truth domain is N then the truth set is {1, 5}
One way to turn a predicate P(x) into a statement is to use the
universal quantifier, which is the symbol ∀ and means “for all”
(“for any”, “for each”).
DEFINITION: Let Q(x) be a predicate and D be the truth domain
for x. A universal statement is a statement of the form
∀x ∈ D, Q(x).
It is true if and only if Q(x) is true for every x in D. If there is
any x in D for which Q(x) is false, the universal statement will
be false. The value of x for which Q(x) is false is called a
counterexample for the universal statement.
Ex. Let D = {−5, 8, 9, 11} and consider the statement
∀x ∈ D, x 2 + x > 2
Show that this statement is true:
Solution: We check that x 2 + x > 2 is true for all x ∈ D. (This is
called the method of exhaustion)
(−5)2 + (−5) > 2
82 + 8 > 2
92 + 9 > 2
112 + 11 > 2
∀x ∈ D, x 2 + x > 2 is true.
Ex. Now show that ∀x ∈ R, x 2 + x > 2 is false
Solution: It suffices to find one value of x ∈ R for which it is not
the case that x 2 + x > 2. In other words, we are looking for a
counterexample in R.
One such counterexample is x = −1:
(−1)2 + (−1) 6> 2
Therefore ∀x ∈ R, x 2 + x > 2 is false.
Another way to turn a predicate Q(x) into a statement is to use
the existential quantifier, ∃, which means “there exists” (“there
is a ”, “for some”, “there is at least one”).
DEFINITION: Let Q(x) be a predicate and D the truth domain of
x. An existential statement is a statement of the form
∃x ∈ D such that Q(x).
It is true if and only if Q(x) is true for at least one element of x
of D. It will be false if Q(x) is false for all x ∈ D.
Ex. Show that the statement “∃n ∈ Z such that n2 = n is true.
Solution: It suffices to find one integer such that n2 = n.
Obviously, one such integer is n = 1.
Ex. Given the truth domain A = {2, −7, 3, 5}, show that the
existential statement
∃n ∈ A such that n2 = n
is false.
22 6= 2
(−7)2 6= −7
33 6= 3
52 6= 5
2
Since there is no element n ∈ A for which n = n, this
existential statement is false.
Solution: Clearly
Given a statement involving quantifiers, it is generally possible
to translate it into English in a variety of ways:
Ex. ∀x ∈ R, x 2 ≥ 0
This can be translated as
• The square of every real number is non-negative.
• Every real number has a non-negative square.
• x has a non-negative square, for any real number x.
• No real number can have a negative square.
One of the most common types of universal statements is the
universal conditional statement:
∀x, if P(x) then Q(x).
Ex. Translate the following statements:
(a) ∀x ∈ R, if x ≥ 3, then x 2 ≥ 9
translation: “if a real number is at least 3,
then its square is at least 9.
(b) “no bird is a mammal”
translation: ∀x, if x is a bird, then x is not a
mammal.
• Consider the statement ∀x, if x ∈ Z, then x ∈ Q.
• We can rewrite it as: ∀x ∈ Z, x ∈ Q.
[we restricted the truth domain to integers]
• Consider the statement ∀x ∈ D, P(x).
• We can rewrite it as: ∀x, if x ∈ D, then P(x).
Consider the statement “if a number is an integer, then it is a
rational number”.
• Although it is a universal statement, it does not contain the
key words “all” or “every” or “any” or “each”. This is an example
of an implicit universal quantification.
Consider the statement “the number 24 can be written as a
sum of two even integers”.
• This is an example of an implicit existential quantification and
we could rewrite it as “∃ even integers m and n such that
24 = m + n.
DEFINITION: If P(x) and Q(x) are predicates with the same
domain D, the notation
P(x) ⇒ Q(x)
means that every element of x ∈ D which is in the truth set for
P(x) is also in the truth set of Q(x). Equivalently,
∀x, P(x) → Q(x).
The notation P(x) ⇔ Q(x) means that the universal statement
∀x, P(x) ↔ Q(x)
is true (P(x) and Q(x) have the same truth sets).
Ex. Let
Q(n) be “n is a factor of 8”;
R(n) be “n is a factor of 4”;
S(n) be “n < 5 and n 6= 3”
and suppose the domain of n is N.
The truth sets are:
Q(n) : {1, 2, 4, 8}
R(n) : {1, 2, 4}
S(n) : {1, 2, 4}
Then R(n) ⇔ S(n),
R(n) ⇒ Q(n),
S(n) ⇒ Q(n).
2.2 - Introduction to Predicates and Quantified Statements
II
NEGATION OF A UNIVERSAL STATEMENT THEOREM: The
negation of a statement of the form ∀x ∈ D, Q(x) is logically
equivalent to a statement of the form
∃x ∈ D such that ∼ Q(x).
We can write it as
∼ ∀x ∈ D, Q(x) ≡ ∃x ∈ D such that ∼ Q(x).
Ex. the negation of “All engineering students must take
calculus”
is “there are some engineering students who do not have to
take calculus”.
Ex. the negation of “∀ primes p, p is odd”
is “∃ a prime p such that p is not odd.
NEGATION OF AN EXISTENTIAL STATEMENT THEOREM: The
negation of a statement of the form ∃x ∈ D such that Q(x) is
logically equivalent to a statement of the form
∀x ∈ D, ∼ Q(x).
We can write it as
∼ ∃x ∈ D such that Q(x) ≡ ∀x ∈ D, ∼ Q(x).
Ex. the negation of “some birds are mammals”
is “no birds are mammals”.
Ex. the negation of “∃ a triangle T such that the sum of the
angles of T equals 200o ”
is “∀ triangles T , the sum of the angles of T does not equal
200o ”.
Suppose we want to negate a universal conditional statement
∀x, P(x) → Q(x). Then
∼ ∀x, P(x) → Q(x)
≡ ∃ x such that ∼ P(x) → Q(x) .
But,
∼ P(x) → Q(x)
≡
P(x) ∧ ∼ Q(x)
So ∼ ∀x, P(x) → Q(x) ≡ ∃ x such that P(x) ∧ ∼ Q(x) .
Ex. The negation of “∀ integers n, if n is even, then n is
divisible by 4” is
“∃ an integer n such that n is even and n is not
divisible by 4.
Ex. The negation of “∃ a person p such that p is blond and p
does not have blue eyes” is
“∀ people p, if p is blond then p has blue eyes.
Suppose we are looking at quantified statements which refer to
a finite domain
D = {x1 , x2 , . . . , xn }.
Saying the statement
∀x ∈ D, P(x)
is true, is equivalent to saying that P(x) is true for every xi ∈ D:
P(x1 ) ∧ P(x2 ) ∧ · · · ∧ P(xn ).
Saying the statement
∃x ∈ D such that P(x)
is equivalent to the saying that P(x) is true for some xi ∈ D:
P(x1 ) ∨ P(x2 ) ∨ · · · ∨ P(xn ).
Ex. Suppose D = {1, −1} where P(x) is the predicate x 2 = 1
and Q(x) is the predicate x 2 = x.
Then ∀x ∈ D, P(x) is true because P(1) ∧ P(−1) is true.
And ∃x ∈ D such that Q(x) is true because Q(1) ∨ Q(−1) is
true.
• If we have a universal statement ∀x ∈ D, if P(x) then Q(x),
then the statement is vacuously true if and only if P(x) is false
for every x ∈ D.
DEFINITION: Consider a universal conditional statement
∀x ∈ D, if P(x) then Q(x).
(1) Its contrapositive is ∀x ∈ D, if ∼ Q(x) then ∼ P(x).
(2) Its converse is ∀x ∈ D, if Q(x) then P(x).
(3) Its inverse ∀x ∈ D, if ∼ P(x) then ∼ Q(x).
Ex. Consider the statement ∀x ∈ R, if x > 2 then 3x + 2 > 8.
Contrapositive:
Converse:
Inverse:
∀x ∈ R, if 3x + 2 6> 8 then x 6> 2.
∀x ∈ R, if 3x + 2 > 8 then x > 2.
∀x ∈ R, if x 6> 2 then 3x + 2 6> 8.
• The usual equivalences (and non-equivalences) are also true
for universal conditional statements; namely:
conditional statement ≡ its contrapositive
conditional statement 6≡ its converse
conditional statement 6≡ its inverse
converse ≡ inverse.
Added: January 22
Ex. Negate the following statements:
(1) “some people like red"
“it is not true that some people like red”
“no people like red”
“∀ people p, p does not like red”
(2) “all dogs are loyal”
“it is not true that all dogs are loyal”
“some dogs are disloyal”
“∃ a dog d such that d is disloyal”
(3) “The sum of any two irrational numbers is irrational”
“it is not true that the sum of any two irrational numbers
is irrational"
“there are some irrational numbers whose sum is
rational”
“∃ irrational numbers m, n such that m + n is rational”
Added: January 22
(4) “The product of any irrational number and any rational
number is irrational”
“It is not true that the product of any irrational number
and rational number is irrational”
“there exists an irrational number and a rational number
whose product is not irrational”
Added: January 22
Consider rewording the original sentence:
“∀ rational numbers q and irrational numbers i, (q · i) is
irrational”
“∀ q ∈ Q and i ∈ I, (q · i) ∈ I”
(where I is the set of irrational numbers)
The negation was: “there exists an irrational number and a
rational number whose product is not irrational"
/ I”
In other words: ∃ q ∈ Q and i ∈ I such that (q · i) ∈
Generally, ∼ (∀x ∈ D, Q(x)) ≡ ∃x ∈ D such that ∼ Q(x)
and
∼ (∃x ∈ D such that Q(x)) ≡ ∀x ∈ D, ∼ Q(x)
Added: January 22
(5) “For all integers n, if n2 is even then n is even.”
“It is not true that for all integers n, if n2 is even then n
ambiguous
is even.”
So how to we negate conditional statements?
Let Q(n) be “if n2 is even, then n is even”.
So our statement becomes ∀ integers n, Q(n).
The negation is: “it is not true that ∀ integers n, Q(n)”
Or simply “∃ some integer n such that ∼ Q(n)”
Now we need to negate Q(n): ∼ if n2 is even, then n is even
Added: January 22
∼
if
n2
is even, then n is even
We did this back in Section 1.2:
∼ (p → q) ≡ ∼ (∼ p ∨ q)
≡ ∼ (∼ p) ∧ (∼ q)
≡ p∧∼q
∼
if n2 is even, then n is even ≡ n2 is even and n is odd
Added: January 22
So back to the question:
(5) “For all integers n, if n2 is even then n is even.”
We gave the negation to be:
“∃ some integer n such that ∼ Q(n)”
But ∼ Q(n) is “n2 is even and n is odd”
We now have:
“∃ some integer n such that n2 is even and n is odd.”
In general,
∼ ∀x ∈ D, if P(x) then Q(x)
≡ ∃x ∈ D such that P(x) and ∼ Q(x)
Added: January 22
(6) “∀ people p, if p is blond, then p has blue eyes.”
Again, we can treat this as “∀ people p, Q(p)”.
Then the negation is “∃ people p such that ∼ Q(p)”.
Which is simply
“∃ people p such that p is blond and p does not have blue eyes.”
Added: January 22
Ex. Negate the following:
(7) “If an integer is divisible by 2, then it is even.”
(8) For every real number x, if x(x + 1) > 0 then x > 0 or
x < −1
Added: January 22
Ex. Negate the following:
(7) “If an integer is divisible by 2, then it is even.”
Equivalently,
∀x ∈ Z, if x is divisible by 2, then x is even.
∀x ∈ Z, if P(x) then Q(x)
Negation:
∃x ∈ Z such that P(x) and ∼ Q(x)
Answer:
∃x ∈ Z such that x is divisible by 2 and x is not even.
Added: January 22
(8) For every real number x, if x(x + 1) > 0 then x > 0 or
x < −1
Equivalently, ∀x ∈ R, if P(x) then Q(x)
where P(x) = x(x + 1) > 0 and Q(x) = x > 0 or x < −1
Negation: ∃x ∈ R such that P(x) and ∼ Q(x).
DeMorgan’s
Law:
∼ (x > 0) ∨ (x < −1) ≡ ∼ (x > 0) ∧ ∼ (x < −1)
≡ (x ≤ 0) ∧ (x ≥ −1)
Answer:
∃x ∈ R such that x(x + 1) > 0 and both x ≤ 0 and x ≥ −1
Modified: January 22
DEFINITION:
(1) “∀x, P(x) is a sufficient condition for Q(x)” means
“∀x, if P(x) then Q(x)”.
Ex. ∀ people p, if p is eligible to vote, then p is at least 18
years old.
The truth of the condition of “p is eligible to vote" is sufficient to
ensure the truth of the condition “p is at least 18 years old."
(2) “∀x, P(x) only if Q(x)” means
∀x, if ∼ Q(x), then ∼ P(x)”
or, equivalently “∀x, if P(x) then Q(x).
Modified: January 22
(3) “∀x, P(x) is a necessary condition for Q(x)” means
“∀x, if ∼ P(x) then ∼ Q(x)”
or equivalently ∀x, if Q(x) then P(x).
Ex. ∀ people p, if p is at least 18 years old then p is eligible to
vote.
The condition of “p is at least 18 years old" is necessary for the
condition “p is eligible to vote."
If p were younger than 18, then p would not be eligible to vote.
Modified: January 22
Ex. Rewrite each as a universal conditional statement:
(a) Squareness is a sufficient condition for rectangularity.
∀x, if x is a square, then x is a rectangle.
(b) A product of two integers is odd only if both of them are odd.
∀m, n ∈ Z, if mn is odd, then m, n are both odd
2.3 - Statements Containing Multiple Quantifiers
Consider the statement ∀x ∈ R, ∃y ∈ R, such that x < y
What it means: For every real number x, there is a larger real
number y. (TRUE)
Consider the statement ∃y ∈ R, such that ∀x ∈ R, x < y
What it means: There exists a real number y such that it is
larger than any real number x. (FALSE)
Conclusion: By reversing the order of quantifiers in a
statement, that statement may change considerably.
Question: Given a statement of the form
∀x ∈ D, ∃y ∈ E such that P(x, y)
or
∃x ∈ D such that ∀y ∈ E , P(x, y)
how do we verify whether such a statement is true or false?
To check the truth value of the statement
∀x ∈ D, ∃y ∈ E such that P(x, y)
we can think of it as a game:
• allow someone else to pick any element x ∈ D.
• you must respond by finding an element y ∈ E that “works”
for that particular x.
• if you have no response, then you lose and the statement
must be false. If you can always respond with a good choice of
y, then you win and the statement is true.
Ex.2.3, 9 Let D = E = {−2, −1, 0, 1, 2} Is the following true?
∀x ∈ D, ∃y ∈ E such that x + y = 0
For each element in D, we must be able to find an element in E
that makes the sum of the two elements equal to 0:
If x
If x
If x
If x
If x
= −2, then we choose y = 2
= −1, then we choose y = 1
= 0, then we choose y = 0
= 1, then we choose y = −1
= 2, then we choose y = −2
Yes, the statement is true.
[Alternately, for each integer x ∈ D, the integer −x is in D as
well, including 0 and for all integers x, x + (−x) = 0.]
To check the truth value of the statement
∃x ∈ D, such that ∀y ∈ E , P(x, y)
we can think of it as a game:
• we choose one fixed element x ∈ D
• your opponent tries to find a value of y ∈ E for which P(x, y)
fails
• if your opponent can find no such value for y, then you have
won and the statement is true. If your opponent finds a y ∈ E
which disproves P(x, y), then you have lost and the statement
is false.
Ex. 2.3, 9 Let D = E = {−2, −1, 0, 1, 2}. Is the following true?
∃x ∈ D such that ∀y ∈ E , x + y = y
Let us choose x = 0. Then 0 + y = y for any y ∈ E because
the elements of E are real numbers.
The reciprocal of a real number a is a real number b such that
ab = 1.
Ex. Rewrite these true statements using quantifiers and
variables:
(a) Every nonzero real number has a reciprocal
∀ nonzero real number x, ∃y ∈ R such that xy = 1.
(b) There is a real number with no reciprocal
∃z ∈ R such that ∀u ∈ R, zu 6= 1.
(c) There is a smallest positive integer
∃m ∈ N such that ∀n ∈ N, m ≤ n.
Suppose we want to negate the statement
∀x ∈ D, ∃y ∈ E such that P(x, y)
Then, we have
∼ ∀x ∈ D, ∃y ∈ E such that P(x, y)
≡ ∃x ∈ D such that ∼ ∃y ∈ E such that P(x, y)
≡ ∃x ∈ D such that ∀y ∈ E , ∼ P(x, y)
Similarly,
we can show that
∼ ∃x ∈ D such that ∀y ∈ E , P(x, y)
≡ ∀x ∈ D, ∃y ∈ E such that ∼ P(x, y).
As we have seen, the order of quantifiers matters. However, if
the quantifiers are identical, then the order is irrelevant.
Ex. ∀x ∈ R and ∀y ∈ R, x · y = y · x is logically equivalent to
∀y ∈ R and ∀x ∈ R, x · y = y · x
(similarly if there are two existential quantifiers).
Note: The following is also true
(1) ∀x ∈ D, P(x) ≡ ∀x x ∈ D → P(x)
(2) ∃x ∈ D, P(x)
≡
∃x x ∈ D ∧ P(x) .
Added: January 22
(1) ∀x ∈ D, P(x)
≡
∀x x ∈ D → P(x)
Ex. “For every x ∈ Z, 3x 4 + 7 is positive.”
Equivalently, ∀x, if x ∈ Z then 3x 4 + 7 is positive
(2) ∃x ∈ D, P(x)
≡
∃x x ∈ D ∧ P(x) .
Ex. “There exists a black dog d such that d has brown eyes.”
Equivalently, ∃ a dog d d ∈ D and d has brown eyes where
D is the set of all black dogs.