Download Document

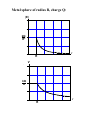
EXAMPLE: How much energy is required to
assemble this arrangement of charges?
Q1 = +2.0 µC
m
20
c
m
c
20
Q2 = +4.0 µC
20 cm
Q3 = +6.0 µC
Q1 = +2.0 µC
W1=0
20
cm
Q1 = +2.0 µC
Q2 = +4.0 µC
9 × 109 × 2 × 10−6
W2 =
× 4 × 10−6
0.2
W2 = 0.36 J
Q1 = +2.0 µC
m
20
c
m
c
20
Q2 = +4.0 µC
20 cm
Q3 = +6.0 µC
9 × 109 × 2 × 10−6
W3 =
× 6 × 10−6 +
0.2
9 × 109 × 4 × 10−6
× 6 × 10−6
0.2
W3 = 0.36 J
Wtotal = W1 + W2 + W3
= 0.0 + 0.36 + 1.62
= 1.98 J
POTENTIAL DUE TO CONTINUOUS
CHARGE DISTRIBUTIONS
Potential due to a point charge is
kQ
V=
r
Divide charge distribution into small
quantities dQ. The resulting small
contribution dV to the potential at a point a is
then
dVa =
kdQ
r
The total potential at point a is obtained by
summing the contributions dVa for all the
elements of charge dQ
dQ
Va = k
r
∫
EXAMPLE: A charge Q is uniformly
distributed on a thin ring of radius a. What is
the potential on the axis and at a distance z
from the center of a ring of charge?
dV
r = a 2 + z2
θ
r
dl
z
a
dQ
V(z) = k
=k
r
∫
=k
2πa
∫
0
1
Q
2π a a2 + z2
λ dl
a 2 + z2
2πa
∫
0
dl =
kQ
a 2 + z2
EXAMPLE: A charge Q is uniformly
distributed on a thin disk of radius R. What is
the potential on the axis and at a distance z
from the center of a ring of charge?
dV
z
Q
σ=
π R2
a2 + z2
da
a
R
Q
π a d a = 2 2 a da
dQ = σ 2π
R
R
kdQ
2kQ R a da
V(z) =
= 2
2
2
2
2
R
+
z
+
z
a
a
0
0
∫
2kQ
= 2
R
∫
(
)
z2 + R 2 − z
EXAMPLE: A charge Q is distributed
−L and x=0.
uniformly on the x-axis between x=−
What is the potential on the y-axis?
y
dV
x'2 +y2
Q
λ=
L
−L
dx'
V ( y) =
0
∫
−L
x
0
k λ dx'
∫
[
]
kQ 0 dx'
=
2
2
2
2
L
y
+
x' +y
x
'
−L
kQ
=
ln x'+ x'2 + y2
L
0
−L

kQ 
y
V ( y) =
ln 2

2
L  L + y − L 
Potential Gradient
∆V = Vb - Va = −Vba
b
∫
r r
Vba = ∆V = − E ⋅ dl
a
r r
−dV = E ⋅ d l = Exdx + Eydy + Ezdz
r
∂V ˆ ∂V ˆ ∂V 

ˆ
E=− i
+j
+k
∂y
∂z 
 ∂x
Work = Force × Distance
Work
Potential Difference = ∆ V =
Charge
W
F × ∆s
∆V =
=
Q
Q
F
∆V =
× ∆s
Q
= E × ∆s
∆V
E=
∆s
1 N/C = 1 V/m
EQUIPOTENTIAL SURFACES
These are imaginary or real surfaces,
every point of which is at the same potential.
Electric field lines are ⊥ to equipotential
surfaces.
Metal surfaces are equipotential surfaces.
EXAMPLE:
Equipotential surfaces for a point charge are
spherical surfaces centered on the charge.
+Q
Conducting Sphere Characteristics:
If an equipotential surface is replaced by a
thin conducting shell, then the fields and
potentials are unchanged.
+
+
+
+
+
+
+
+
-
-
+
+
-
+
-
-
+
+
-
-
-
+Q
-
+
+
-
+
+
- - -+ +
-
+
+
+
-
- - +
+
+
+
+
+
-
-+
+
+
+
+
+
+
+
1. On an isolated conducting sphere the
charge is uniformly distributed on the
outside surface.
2. In regions outside the sphere, the electric
field and potential are the same as though
all the charge was a point charge at the
center of the sphere.
3. Inside a conducting sphere the electric
field is zero, and the potential is constant
with a value equal to that at the surface.
Let the radius of a conducting sphere be R,
then for points outside of the sphere,
r≥R
kQ
E= 2
r
kQ
V=
r
At the conducting surface,
r=R
kQ
Es = 2
R
kQ
Vs =
R
Vs = R E s
Thus,
Inside the conducting surface, the field and
potential are constant.
r>R
Ei = 0
kQ
Vi =
R
Metal sphere of radius R, charge Q:
|E|
2.00
1.50
kQ
1.00
R2
0.50
r
0.00
0.0
R
1.0
2.0
3.0
4.0
5.0
V
2.00
1.50
kQ
1.00
R
0.50
r
0.00
0.0
R
1.0
2.0
3.0
4.0
5.0