Download Electric Potential

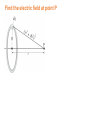
Electric Potential
Which group of charges took more work to bring together
from a very large initial distance apart?
+1
d
+2
+1
d
+1
Both took the same amount of work.
d
d
+1
1) V > 0
What is the electric
potential at point A?
2) V = 0
3) V < 0
A
B
1) V > 0
What is the electric
field at point B?
2) V = 0
3) V < 0
A
B
1) P  1
Which requires the most work,
to move a positive charge from
P to points 1, 2, 3 or 4 ? All
points are the same distance
from P.
2) P  2
3) P  3
4) P  4
5) all require the same
amount of work
3
2
1
P

E
4
Relation between Electric Potential and Electric
Field
The general relationship
between a conservative force
and potential energy:
Substituting the
potential difference
and the electric field:
Relation between Electric Potential and Electric
Field
The simplest case is a uniform field:
𝒃
𝚫𝐕 = −
𝑬 ∙ 𝒅ℓ
𝒂
Electric Potential Due to Point Charges
To find the electric potential due to a point
charge, integrate the field along a field line:
𝑉𝑏 − 𝑉𝑎 = −
𝑟𝑏
𝑟𝑎
𝑄
𝐸 ∙ 𝑑ℓ = −
4𝜋𝜖𝑜
𝑟𝑏
𝑟𝑎
1
𝑑𝑟
2
𝑟
𝑄
1 1
=
−
4𝜋𝜖𝑜 𝑟𝑏 𝑟𝑎
Choosing V=0 at infinity
i.e. 𝒓𝒂 = ∞
𝑞
Potential created by a point charge
𝑉 = 𝑘𝑒
at a distance r from the charge.
𝑟
Determine the potential at a distance r from the
center of a uniformly charged conducting sphere
of radius r0 for
(a) r > r0,
(b) r = r0,
(c) r < r0.
The total charge on the sphere is Q.
Potential Due to Any Charge Distribution
The potential due to an arbitrary charge
distribution can be expressed as a sum or
integral (if the distribution is continuous):
or
A thin circular ring of radius R has a uniformly
distributed charge Q. Determine the electric
potential at a point P on the axis of the ring a
distance x from its center.
Equipotential Surfaces
An equipotential is a line
or surface over which the
potential is constant.
Electric field lines are
perpendicular to
equipotentials.
The surface of a conductor
is an equipotential.
Equipotential Surfaces
For a single point charge
with Q = 4.0 × 10-9 C,
sketch the equipotential
surfaces (or lines in a
plane containing the
charge) corresponding
to V1 = 10 V, V2 = 20 V,
and V3 = 30 V.
Equipotential Surfaces
Equipotential surfaces are always
perpendicular to field lines; they are
always closed surfaces (unlike field lines,
which begin and end on charges).
Equipotential Surfaces
A gravitational analogy to equipotential surfaces
is the topographical map – the lines connect
points of equal gravitational potential (altitude).
E 𝐸 Determined from V
If we know the field, we can determine the
potential by integrating. Inverting this
process, if we know the potential, we can
find the field by differentiating:
𝑑𝑉
𝐸ℓ = −
𝑑ℓ
This is a vector differential equation.
Find the electric field at point P
The Electron Volt
One electron volt (eV) is the energy gained by
an electron moving through a potential
difference of one volt:
1 eV = 1.6 × 10-19 J.
The electron volt is often a much more
convenient unit than the joule for measuring
the energy of individual particles.
Practice Problem:
Three charges are placed as shown in the
figure. The distances “a” and “b” are known.
The charges on the x axis are known and
negative (-q1). The charge q2 at y=-b is
unknown.
What must the charge q2 be if the electric
field is zero at some point p at (0,h)?
𝟐𝒒𝟏 𝒉 𝒃 + 𝒉 𝟐
𝒂𝟐 + 𝒉𝟐 𝟑/𝟐