* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download circle… - cmasemath
List of regular polytopes and compounds wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Coxeter notation wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Tessellation wikipedia , lookup
Technical drawing wikipedia , lookup
Perspective (graphical) wikipedia , lookup
Mirror symmetry (string theory) wikipedia , lookup
History of trigonometry wikipedia , lookup
Integer triangle wikipedia , lookup
Perceived visual angle wikipedia , lookup
Complex polytope wikipedia , lookup
Event symmetry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Multilateration wikipedia , lookup
Trigonometric functions wikipedia , lookup
Shapley–Folkman lemma wikipedia , lookup
Line (geometry) wikipedia , lookup
Compass-and-straightedge construction wikipedia , lookup
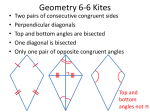
CIRCLE… My edge is a closed convex curve. My diameter is the same no matter where it is measured. I have infinitely many lines of symmetry. All points on my edge are the same distance to my center. If you know the distance from my center to the edge you can know so much more about me…diameter, circumference, and area. No matter my size, my diameter is equal to the ratio of my circumference to Pi. What am I? OVAL… My edge is a closed convex curve. I have two lines of symmetry. The most extreme point on one end or side, is the same distance from my center as the most extreme point on the opposite end or side. For any other point on my edge there are three additional points that are equidistance from my center. What am I? TRIANGLE… I am a convex polygon. I have no parallel sides. I may have three lines of symmetry, one line of symmetry, or none. My angles may vary in size. I may have an obtuse angle, or a right angle, but I cannot have both. I will always have at least two acute angles. It is not possible to have a polygon with fewer sides or angles than I have. If you put all my angles together I make half of a circle. What am I? SQUARE… I am a convex polygon. I am a quadrilateral. I have two pairs of parallel and congruent sides. My angles must all be the same size. My diagonals are congruent. My diagonals are perpendicular to one another. My diagonals bisect one another. I am a parallelogram, but I also have a more specific name. I am a regular shape. I am a rectangle, but I also have a more specific name. All my sides are the same length. I have four lines of symmetry. What am I? RECTANGLE… I am a convex polygon. I am a quadrilateral. I have two pairs of parallel and congruent sides. My angles must all be the same size. My diagonals are congruent. My diagonals bisect one another. I am a parallelogram, but I also have a more specific name. My opposite sides are the same length. I have two lines of symmetry. What am I? PARALLELOGRAM… I am a convex polygon. I am a quadrilateral. I have two pairs of parallel and congruent sides. My diagonals bisect one another. My opposite sides are the same length. My opposite angles must be the same size. I do no have to have any lines of symmetry. What am I? RHOMBUS… I am a convex polygon. I am a quadrilateral. I have two pairs of parallel and congruent sides. My diagonals are perpendicular to one another. My diagonals bisect one another. I am a parallelogram, but I also have a more specific name. I have two lines of symmetry. What am I? TRAPEZOID… I am a convex polygon. I am a quadrilateral. I have one pair of parallel sides. I have a pair of legs that are opposite one another. My legs are not parallel and may not be the same length. My angles may vary in size. I can have no more than two right angles. I can have no more than two obtuse angles. I can have an obtuse angle with two right angles, but I cannot have a right angle with two obtuse angles. What am I?