Download Section 1.1

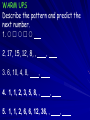
WARM UPS
Describe the pattern and predict the
next number.
1.     
2. 17, 15, 12, 8, ,
3. 6, 10, 4, 8,
,
,
4. 1, 1, 2, 3, 5, 8, ,
5. 1, 1, 2, 6, 6, 12, 36, ,
,
,
ANSWERS
1)      
Circle, Square, Circle, Square, repeat
2) 17, 15, 12, 8, 3 , – 3
Subtract 2, Subtract 3, Subtract 4, . . .
or
Add – 2, Add – 3, Add – 4, . . .
3) 6, 10, 4, 8, 2 , 6
Add 4, Subtract 6, Add 4, . . .
ANSWERS
4. 1, 1, 2, 3, 5, 8, , 13 , 21
A number is found by adding the two
numbers before it
2=1+1 3=1+2
5=2+3
5. 1, 1, 2, 6, 6, 12, 36, , 36 , 72
Multiply by 1, Multiply by 2, Multiply by 3,
repeat
Chapter 1
Tools of Geometry
Sec 1 – 1
Patterns and Inductive Reasoning
Objectives/Assignment:
Find and describe patterns.
– Today’s WARM UPS
Use inductive reasoning to make real-life
conjectures.
Finding & Describing Patterns
Geometry, like much of mathematics and
science, developed when people began
recognizing and describing patterns.
In this course, you will study many amazing
patterns that were discovered by people
throughout history and all around the world.
You will also learn how to recognize and
describe patterns of your own. Sometimes,
patterns allow you to make accurate predictions.
Vocabulary
Inductive Reasoning: The process of
making conjectures based on observed
patterns.
Inductive Reasoning
1. Look for a pattern.
2. Make a conjecture.
3. Prove the conjecture or find a
counterexample.
Vocabulary
Conjecture: An unproven statement
based on observation.
The next shape is a square.
Conjecture: Based on the pattern, the next
shape is a square.
Vocabulary
Counterexample: An example that
proves a statement false.
Statement: Two odd numbers added
together is always odd.
Counterexample: 3 + 5 = 8 (8 is even)
TRY
Show the conjecture is false by
finding a counterexample.
The difference of two positive
numbers is always positive.
Inductive Reasoning
1. Look for a pattern.
2. Make a conjecture - an unproven statement
that is based on observations.
3. Prove the conjecture or find a
counterexample - an example that shows a
conjecture is false.
Using Inductive Reasoning
1. Look for a Pattern: Look at several
examples. Use diagrams and tables to help
discover a pattern.
EX. 1 Find the next term in the sequence:
243
81 ____
A) 1, 3, 9, 27, ___,
Rule: x 3
40
B) - 5 ,- 2, 4,13, ___,
25 ___
Rule: +3, +6, +9, +12, …
48 ___
96
C) 3, 6, 12, 24, ___,
Rule: x2
D) 1, 2, 4, 7, 11, 16, 22, ___,
29 ___
37 Rule: +1, +2, +3, +4, …
Using Inductive Reasoning
2. Make a Conjecture. A conjecture is an unproven
statement that is based on observations. Discuss
the conjecture with others. Modify the conjecture, if
necessary.
EX. 2 Complete the conjecture. The sum of the
first n odd positive integers is ?.
How to proceed:
List some specific examples and look for a
pattern.
Ex. 2: Making a Conjecture
The sum of the first n odd positive integers is ?.
1 = 12
1 + 3 = 4 = 22
1 + 3 + 5 = 9 = 32
1 + 3 + 5 + 7 = 16 = 42
1 + 3 + 5 + 7 + 9 = 25 = 52
1 + 3 + 5 +...+ 30 = 900 = 302
The sum of the first n odd positive integers is n2.
Using Inductive Reasoning
3. Verify the conjecture.
a. To prove that a conjecture is true, you
need to prove it is true in all cases.
b.To prove that a conjecture is false, you
need to provide a single counterexample
Finding a Counterexample
EX. 3 The first 3 odd prime numbers are 3, 5, 7.
Make a conjecture about the 4th.
11
– 3, 5, 7, ___
– One would think that the rule is add 2, but that
gives us 9 for the fourth prime number.
Is that true?
– What is the next odd prime number?
Finding a Counterexample
EX 4 Show the conjecture is false by finding
a counterexample.
Conjecture: Everybody is this classroom is
wearing a red shirt for Friday Spirit Day.
Counterexample: Name anyone that is not
wearing a red shirt.
Note:
Not every conjecture is known to be true
or false. Conjectures that are not known
to be true or false are called unproven or
undecided.
Ex. 5: Examining an Unproven
Conjecture
In the early 1700’s, a Prussian mathematician
names Goldbach noticed that many even
numbers greater than 2 can be written as the
sum of two primes.
Specific cases:
4=2+2
6=3+3
8=3+5
10 = 3 + 7
12 = 5 + 7
14 = 3 + 11
16 = 3 + 13
18 = 5 + 13
20 = 3 + 17
Ex. 5: Examining an Unproven
Conjecture
Conjecture: Every even number greater than 2
can be written as the sum of two primes.
This is called Goldbach’s Conjecture. No one
has ever proven this conjecture is true or found
a counterexample to show that it is false. As of
the writing of this text, it is unknown if this
conjecture is true or false. It is known; however,
that all even numbers up to 4 x 1014 confirm
Goldbach’s Conjecture.
Ex. 6: Using Inductive Reasoning
in Real-Life
Moon cycles. A full moon occurs when the
moon is on the opposite side of Earth from
the sun. During a full moon, the moon
appears as a complete circle.
Ex. 6: Using Inductive Reasoning
in Real-Life
Use inductive reasoning and the
information below to make a conjecture
about how often a full moon occurs.
Specific cases: In 2005, the first six full
moons occur on January 25, February 24,
March 25, April 24, May 23 and June 22.
A full moon occurs every 29 or 30 days.
This conjecture is true. The moon
revolves around the Earth approximately
every 29.5 days.
Assignment #1 pp. 6-8
# 12 – 28 even
34 – 38 even
47, 48
52 – 70 even
GEOMETRY LESSON 1-1
The price of overnight shipping was $8.00 in 2000, $9.50
in 2001, and $11.00 in 2002. Make a conjecture about the
price in 2003.
Write the data in a table. Find a pattern.
2000
2001
2002
$8.00
$9.50
$11.00
Each year the price increased by $1.50.
A possible conjecture is that the price in 2003 will increase by $1.50.
If so, the price in 2003 would be $11.00 + $1.50 = $12.50.
1-1
GEOMETRY LESSON 1-1
Pages 6–9 Exercises
1. 80, 160
12. 1 , 1
5 6
2. 33,333; 333,333 13. James, John
3. –3, 4
14. Elizabeth, Louisa
4.
15. Andrew, Ulysses
1 1
16 , 32
5. 3, 0
16. Gemini, Cancer
6.
17.
1
1, 3
7. N, T
8. J, J
19. The sum of the first 6 pos.
even numbers is
6 • 7, or 42.
20. The sum of the first 30 pos
even numbers is
30 • 31, or 930.
21. The sum of the first 100
pos. even numbers is
100 • 101, or 10,100.
18.
9. 720, 5040
10. 64, 128
1 1
11. 36 , 49
1-
GEOMETRY LESSON 1-1
22. The sum of the first
100 odd numbers is
1002, or 10,000.
28. 1 ÷ 1 = 3 and 3 is
2
3
2
2
improper.
29. 75°F
25–28. Answers may vary.
Samples are given.
25. 8 + (–5 = 3) and 3 >/ 8
26.
1 • 1 > 1 and 1 • 1 > 1
/
/ 2
3 2
3 2 3
27. –6 – (–4) < –6 and
–6 – (–4) < –4
32. 10, 13
33. 0.0001, 0.00001
23. 555,555,555
24. 123,454,321
31. 31, 43
30. 40 push-ups;
answers may vary.
Sample: Not very
confident, Dino may
reach a limit to the
number of push-ups
he can do in his
allotted time for
exercises.
1-1
34. 201, 202
35. 63, 127
36. 31 , 63
32 64
37. J, S
38. CA, CO
39. B, C
GEOMETRY LESSON 1-1
40. Answers may vary.
Sample: In Exercise
31, each number
increases by increasing
multiples of 2. In Exercise
33, to get the next term,
divide by 10.
42.
43.
44.
41.
45.
You would get a third line
between and parallel to
the first two lines.
46. 102 cm
1-1
47. Answers may vary.
Samples are given.
a. Women may soon outrun
men in running competitions.
b. The conclusion was based
on continuing the trend
shown in past records.
c. The conclusions are
based on fairly recent
records for women,
and those rates of
improvement may not
continue. The conclusion
about the marathon is most
suspect because records
date only from 1955.
GEOMETRY LESSON 1-1
48. a.
b. about 12,000 radio
stations in 2010
c. Answers may vary.
Sample: Confident;
the pattern has held
for several decades.
49. Answers may vary.
Sample: 1, 3, 9, 27,
81, . . .
1, 3, 5, 7, 9, . . .
50. His conjecture is
52.
probably false
because most
53.
people’s growth
slows by 18 until
they stop growing
somewhere between
18 and 22 years.
51. a.
b. H and I
c. a circle
21, 34, 55
a. Leap years are years
that are divisible by 4.
b. 2020, 2100, and 2400
c. Leap years are years
divisible by 4, except
the final year of a
century which must
be divisible by 400.
So, 2100 will not be a
leap year, but 2400
will be.
GEOMETRY LESSON 1-1
54. Answers may vary.
Sample:
55. (continued)
d.
100 + 99 + 98 + … + 3 + 2 + 1
1 + 2 + 3 + … + 98 + 99 + 100
101 + 101 + 101 + … + 101 + 101 + 101
56. B
The sum of the first 100 numbers is
57. I
100 • 101 , or 5050.
2
The sum of the first n numbers is n(n+1) .
2
55. a. 1, 3, 6, 10, 15, 21
b. They are the same.
c. The diagram shows the product of n
and n + 1 divided by 2 when
n = 3. The result is 6.
1-1
58. [2] a. 25, 36, 49
b. n2
[1] one part correct
GEOMETRY LESSON 1-1
59. [4] a. The product of 11
and a three-digit
number that begins
and ends in 1 is a
four-digit number
that begins and ends
in 1 and has middle
digits that are each
one greater than the
middle digit of the
three-digit number.
(151)(11) = 1661
(161)(11) = 1771
59. (continued)
[3] minor error in
explanation
60-67.
[2] incorrect description
in part (a)
[1] correct products for
(151)(11), (161)(11),
and (181)(11)
68. B
b. 1991
69. N
c. No; (191)(11) = 2101
70. G
Warm- up #1
1. Sketch the next figure.
2. How many squares are in the next object?
3. Describe the pattern and find the next number.
a. 3, 9, 27, 81, …
b. 97, 63, 18, …
4. Evaluate
(x + 1)
2 for x = 3.
5. Give the coordinates of each point graphed below.
a. Point A
b. Point B
c. Point C
d. Point D
Geometry #1 1.1 p6 (12 – 28even, 34-38even, 47, 48, 52-70 even)
12.
14.
47. E
48. D
52. – 58
16. 13
18. 14641
20. 37
22. 2
24. 16 blocks
26.
Fig 1 2 3 4 5
Dist. 4 8 12 16 20
28. 80 units
34. 2 is prime, but not odd
36. 2 × 17 = 34, but 17 is not even
1
1
1 1
38.
4 = 2 and 2 > 4
60. 9
62. 16
64. 25
66. 8
68. 625
70. 19
Describing a Visual Pattern
Sketch the next figure in the pattern.
1
2
3
4
5