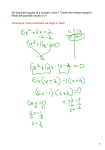* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Patterns, Functions and Algebra
Survey
Document related concepts
Transcript
Lesson 8-1 Multiplying Monomials Mathematics Standards - Number, Number Sense and Operations: Explain the effects of operations such as multiplication or division, and of computing powers and roots on the magnitude of quantities. - Patterns, Functions and Algebra: Generalize patterns using functions or relationships and freely translate among tabular, graphical and symbolic representations. - Patterns, Functions and Algebra: Describe problem situations by using tabular, graphical and symbolic representations. Mathematics Standards - Patterns, Functions and Algebra: Add, subtract, multiply and divide monomials and polynomials. - Patterns, Functions and Algebra: Simplify rational expressions by eliminating common factors and applying properties of integer exponents. - Patterns, Functions and Algebra: Solve real-world problems that can be modeled using linear, quadratic, exponential or square root functions. Vocabulary Monomial Vocabulary Monomial - a number, a variable, or a product of a number and one or more variables. Constant Vocabulary Monomial - a number, a variable, or a product of a number and one or more variables. Constant – A Number Example 1 Determine whether each expression is a monomial. Explain your reasoning. a) 17 – s This is not a monomial because it involves subtraction, not multiplication. Example 1 Determine whether each expression is a monomial. Explain your reasoning. b) ¾ This is a monomial because it is a real number and an example of a constant. Example 1 Determine whether each expression is a monomial. Explain your reasoning. c) c d This is not a monomial because it is the quotient, not the product, of two variables. Example 1 Determine whether each expression is a monomial. Explain your reasoning. d) abc 8 5 51 abc 8 This is a monomial because it is the 1 product of a number, 5 , and three variables. Product of Powers Words: To multiply two powers that have the same base, add the exponents. Example: a a a 4 12 412 or a 16 Example 2 Simplify: (6cd5)(5c5d2) 6 • c • d5 • 5 • c5 • d2 30c6d7 Power of a Power Words: To find the power of a power, multiply the exponents. Example: (k ) k 5 9 59 or k 45 Example 3 3 3 2 Simplify: [( 2 ) ] 332 2 18 2 262,144 Power of a Product Words: To find the power of a product, find the power of each factor. Example: 2xy 3 2 x y 3 3 3 or 8x y 3 3 Example 4 Simplify: 3y 5 z 3 y 2 2 z 5 2 9y z 10 2 2 Simplifying Monomial Expressions To simplify an expression involving monomials 1) each base appears exactly once, 2) there are no powers of powers, and 3) all fractions are in simplest form. Example 5 Simplify: ( 4cd ) ( 3d ) 2 2 3 4 c d ( 3) (d ) 2 2 2 3 2 3 16c d (27)d 6 16(27)c d d 6 2 2 2 432c d 2 8 2 Example 6 Simplify: [(8g h ) ] (2gh ) 22 322 422 5 4 8 g h (2gh ) 4 12 16 5 4 8 g h (2gh ) 12 16 5 4 4,096g h (2gh ) 3 4 2 2 5 4 4 54 4,096g h (2 g h ) 12 16 4 4,096g h (16g h ) 12 16 65,536g h 16 4 20 36 Homework Pg 413 16 – 40 (even) 43 – 45 (all)