Download CHAPTER 29: ELECTROMAGNETIC INDUCTION • So far we have

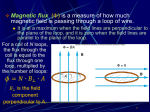
CHAPTER 29: ELECTROMAGNETIC INDUCTION
 So far we have seen that electric charges are the source for both electric and
magnetic fields. We have also seen that these fields can exert forces on other
electric charges. Charges must be moving in order to create a magnetic field
as well as to interact with a magnetic field.
 In this chapter we will study an even deeper connection between electricity
and magnetism. It turns out that electric and magnetic fields themselves
interact with each other directly. We will see that a time-varying magnetic
field can give rise to an electric field and a time-varying electric field can
give rise to a magnetic field.
 This interaction leads to a fundamental understanding of the nature of light
and is also one of the aspects of the universe which led Einstein to his
formulation of the “Special Theory of Relativity”
 This chapter will focus on Faraday’s law (the 4th and last of Maxwell’s
equations) and electromagnetic induction. In addition, we will add a
correction to Ampere’s law, introduced by Maxwell, and this will complete
the theoretical foundation of classical electromagnetism.
Induced Currents
 In each of the figures below there is a coil of wire connected to an ammeter.
If the coil is held stationary and a bar magnet moves toward or away from it,
then a current is induced in the coil. The same also happens if the magnet is
held stationary and the coil moves toward or away from it (b).
 If instead a current-carrying coil moves toward or away from the coil
connected to the meter (or vice-versa), then a current is again induced in the
coil (c).
 Finally, both coils are held stationary and the current in the coil connected to
the battery is varied by opening or closing a switch. During the brief time
while the current is changing, there is a current induced in the coil connected
to the meter (d). Once the current becomes steady the induced current stops
flowing and the ammeter reads zero.
 In each of these situations, there is a current induced in the coil whenever it
is in the presence of a changing magnetic field and the induced current goes
to zero whenever this field stops changing. This phenomenon is known as
electromagnetic induction.
 We have learned that an emf source is needed in order to drive a current in a
circuit. Usually this source, such as a charged capacitor or a battery, is
localized at a particular point in the circuit. The induced emf, however, is
often spread throughout the circuit.
 More careful experimentation has shown that the induced emf is actually
proportional to the rate of change of the magnetic flux thru the coil
FARADAY’S LAW
 First, let’s review the concept of flux for a magnetic field (see figure)
 The total magnetic flux Φ𝐵 [units: T∙m2] through some area is given by the
integral
⃗ ⋅ 𝑑𝑨
⃗⃗ = ∫ 𝐵 cos 𝜙 𝑑𝐴
Φ𝐵 = ∫ ⃗𝑩
 For a uniform magnetic field crossing a flat surface, the magnetic flux is
⃗⃗ ⋅ 𝑨
⃗⃗ = 𝐵𝐴 cos 𝜙
Φ𝐵 = 𝑩
**EXAMPLE #1**
 One of Maxwell’s equations (Gauss’s law for magnetic flux) says that the
⃗ ⋅ 𝑑𝑨
⃗⃗ = 0). Here
magnetic flux thru any closed surface is always zero (∮ ⃗𝑩
⃗⃗ ⋅ 𝑑𝑨
⃗⃗ ).
we are talking about the magnetic flux thru an open surface (∫ 𝑩
 Faraday’s law of induction says that the emf ℰ [units: V] induced in a
conducting loop is equal to and opposite in sign to the rate of change of the
magnetic flux [units: T∙m2/s] thru any surface bounded by that loop
ℰ=−
𝑑Φ𝐵
𝑑𝑡
 Fundamentally, the minus sign in Faraday’s law of induction is a reflection
of the principle of conservation of energy. In practice, this means that the
induced current flows in a direction such that the magnetic field it creates
opposes the change in magnetic flux due to the external magnetic field that
is causing the induced emf ℰ. We will discuss the direction of the induced
current in more detail when Lenz’s law is introduced in the next section.
 First let’s talk about how the magnetic flux thru a surface can change.
Obviously if the magnetic field varies in time, then the flux will change.
Consider the time derivative of the flux written out explicitly:
𝑑
𝑑𝑡
𝑑Φ𝐵
𝑑𝑡
=
(𝐵𝐴 cos 𝜙). The flux will also change if either the area of the surface or
its orientation relative to the magnetic field (i.e., the angle 𝜙 between the
normal to the surface and the magnetic field) varies in time.
 Remember, current is only induced in a conducting loop if there is a
changing flux. The amount of flux has nothing to do with it – what
determines the current is the rate at which the flux is changing.
 One more thing…ℰ = −
𝑑Φ𝐵
𝑑𝑡
is Faraday’s law of induction for a single loop.
If there are N loops that make up a coil, then the total emf induced in the coil
is ℰ = −𝑁
𝑑Φ𝐵
𝑑𝑡
.
**EXAMPLE #2**
**EXAMPLE #3**
**EXAMPLE #4 **
Lenz’s law
 So far we have focused on just calculating the magnitude of the induced
emf. Now we need to talk about the direction of the induced emf –
specifically, the direction of the induced current, whether it flows CW or
CCW around the conducting loop thru which the magnetic flux is changing.
 Imagine a bar magnet moving at a constant velocity towards a stationary
conducting loop of wire with its north pole pointed in the direction of its
motion (shown below)
 The magnetic field strength thru the loop increases as the magnet gets closer.
So the magnetic flux is increasing and, by Faraday’s law, there will be a
current induced in the loop
 Because of the resistance in the loop, electrical energy is dissipated in the
form of heat – where does this energy come from?
 There can only be one source for this energy – whatever is moving the
magnet. This agent must do positive work on the system to offset the loss in
energy due to dissipation.
 Therefore, you must be pushing against some repulsive force. The current
induced in the loop creates its own magnetic field (often referred to as the
“induced field”). As we learned last chapter, the magnetic field of a current
loop is qualitatively very similar to that of a bar magnet – a magnetic dipole.
Like poles repel, therefore the induced current must flow in the direction
indicated in the figure below in order to exert a repulsive force on the
magnet.
 Last chapter, we calculated the magnitude of the magnetic field due to a
current loop and the direction was given by two variations of the RHR:
o the direction of B can be determined by pointing your thumb in the
direction of I and your fingers curl in the direction of the field
o this is equivalent to curling your fingers in the direction of I and your
thumb points in the direction of the field B
 The work done in moving the bar magnet towards the conducting loop
ultimately ends up heating the loop and the interaction of the magnetic fields
is the intermediary of this transfer of energy
 So the direction of the induced current is a reflection of the principle of
conservation of energy; mathematically, this direction is indicated by the
minus sign in Faraday’s law.
 This is the essence of Lenz’s law:
The direction of the induced current is such that the magnetic field
created by the induced current opposes the change in magnetic flux
 I will denote the applied field (the field associated with the changing flux) as
⃗𝑩
⃗ and the field created by the induced current as ⃗𝑩
⃗ 𝑖𝑛𝑑 . Even though a
change in flux (∆Φ𝐵 ) is a scalar quantity, I find it helpful to associate a
“direction” with the change in flux. Consider the figure below.
∆𝚽𝑩
 As discussed earlier, there are three ways that the magnetic flux can change:
o The field strength changes
o The area of any surface bounded by the loop changes
o The orientation of the surface relative to the direction of the field
changes

⃗ give the “direction” of ∆Φ𝐵
Let the direction of the applied field ⃗𝑩
⃗
o An increase in the flux will be taken to be in the same direction as ⃗𝑩
⃗ 𝑖𝑛𝑑 will point in the opposite direction. Point the thumb of
and so ⃗𝑩
⃗ 𝑖𝑛𝑑 and
your right hand (RHR for Lenz’s law) in the direction of ⃗𝑩
your fingers curl in the direction of the induced current (see figure
above).
o A decrease in the flux will be taken to be in the direction opposite to
⃗𝑩
⃗ and so ⃗𝑩
⃗ 𝑖𝑛𝑑 will point in the same direction as ⃗𝑩
⃗ . Point the thumb
⃗ 𝑖𝑛𝑑 and
of your right hand (RHR for Lenz’s law) in the direction of ⃗𝑩
your fingers curl in the direction of the induced current.
 The figures below show four different cases of a changing magnetic flux due
to a change in field strength. Regardless of what is causing the flux to
change, the 2 rules above provide a simple prescription for correctly
applying Lenz’s law in order to determine the direction of the induced
current.
 The rate of change of the magnetic flux sets the emf in a conducting loop.
The resistance of the loop then determines the magnitude of the current
induced in it: 𝐼 =
ℰ
𝑅
gives the induced current
 So the smaller the resistance of the loop, the larger the induced current and
thus the larger the induced magnetic field and the more difficult it is to cause
a change in the flux thru the loop (more work/energy input required)
 Conversely, the larger the resistance of the loop, the smaller the induced
current and thus the smaller the induced magnetic field and the easier it is to
effect a given change in the flux thru the loop (less work/energy input
required)
**GO BACK AND APPLY LENZ’s LAW TO THE EARLIER EXAMPLES
AND GET THE DIRECTIONS OF THE INDUCED CURRENTS**
**EXAMPLE #5 and #6**
Motional Electromagnetic Force
 Let us revisit an example that earlier we analyzed using Faraday’s law and
instead approach it from the perspective of the forces that act on the moving
charges in the conductor, which as usual, we take to be positive
(conventional current)
 By showing that the rate of heating in the loop is precisely equal to the rate
at which the agent pulling the bar does work, we will explicitly show what
we claimed above in introducing Lenz’s law – that energy is conserved.
 In Figure (a) below, the bar is pulled to the right at constant velocity across a
region with a uniform magnetic field that points into the page. The magnetic
⃗ | = |𝑞𝒗
⃗⃗ | = 𝑞𝑣𝐵 and points
⃗ ×𝑩
force on a positive charge in the bar is |𝑭
toward the end of the bar labeled a. As a result, positive charges accumulate
at that end and negative charges accumulate at the opposite end labeled b.
 Because of this separation of charge, an electric field is created that points in




the direction opposite of the magnetic force. Its magnitude grows larger as
more charge accumulates on the ends of the bar until it balances the
magnetic force and the charges are in equilibrium. FE = FB → E = vB
The electric field is also uniform so the potential difference across the bar
(of length L) is ΔV = EL = vBL and the positive end a is at a higher potential
than b (E points “downhill”)
In Figure (b) the moving rod now slides along the rails of a stationary, Ushaped conductor. There is no magnetic force on the charges in the U-shaped
portion (v = 0) but the charge accumulation at a and b create an electric field
that establishes a current in the CCW direction.
So, the moving rod has become like a “battery” – it is a source of emf. This
type of emf is called a motional electromotive force (emf): ℰ = 𝑣𝐵𝐿 [ck
units: (m/s)(N∙s)/(C∙m)(m) = N∙m/C = J/C = V] 
The rate of energy dissipation in the circuit is the product of the emf and the
induced current: 𝑃 = 𝐼ℰ =
ℰ2
𝑅
=
𝐵2 𝐿2 𝑣 2
𝑅
 There is a magnetic force on the bar due to the current flowing thru it in the
⃗ | = |𝐼𝑳
⃗ × ⃗𝑩
⃗ | = 𝐼𝐿𝐵 and by the RHR, this
presence of the applied field, |𝑭
force points to the left. Since the bar is moving at a constant velocity, the
force pulling the bar must be equal and opposite to this force.
⃗ = 𝐹𝑣 = 𝐼𝐿𝐵𝑣 =
 The rate at which this force does work is: 𝑃 = ⃗𝑭 ⋅ 𝒗
ℰ
𝑅
𝐵𝐿𝑣 =
𝐵2 𝐿2 𝑣 2
𝑅
 So all of the energy put into the system by the agent pulling the bar gets
dissipated by the resistance, showing quantitatively that the total energy is
indeed conserved
 In both cases (battery or moving rod) there is a nonconservative electric
force that does positive work on a charge in moving it from b to a (to a
higher potential – “uphill”). This increase in energy is then dissipated in the
form of heat (due to resistance) as it moves from a to b. Since we are talking
about a nonconservative force, the mechanical energy is not conserved but,
as is always true, the total energy is conserved.
 Since the area is increasing, the flux is increasing. Taking the direction of
the magnetic field to indicate the “direction” of an increase in flux, the
induced magnetic field will point in the opposite direction. Using the RHR I
described earlier, point your thumb in the direction of the induced field (out
of page) and your fingers will curl in the direction of the induced current
(CCW).
Generalized Motional Emf
 The above discussion of motional emf induced in a conductor is a specific
case and only considers a uniform magnetic field.
 For an arbitrarily shaped conductor moving in some magnetic field, uniform
or not, the motional emf is given by the closed line integral
⃗⃗ ) ⋅ 𝑑𝒍
⃗ ×𝑩
ℰ = ∮(𝒗
Induced Electric Fields
 For a conductor moving in a magnetic field, the previous discussion shows
that we can understand the induced emf at the microscopic level in terms of
magnetic forces acting on individual charged particles. However, as we have
seen, an emf can be induced in a stationary conductor as well. Can we
understand this at the microscopic level as well?
 Consider a solenoid with n turns (loops) per unit length carrying a steady
current I and encircled by a circular conducting loop of wire as shown in the
figure below.
 Last chapter, we used Ampere’s law to calculate the magnetic field
generated by this distribution of current and found that inside the solenoid, B
= µ0nI and is directed along the axis of the solenoid. Outside of the solenoid,
B = 0.
 Inside the solenoid, B is uniform and so the magnetic flux thru a flat crosssectional area A is just BA = µ0nIA. If the current in the solenoid varies in
time then so does the flux and the induced emf is given by ℰ = |
𝑑𝐼
𝑑Φ𝐵
𝑑𝑡
|=
𝜇0 𝑛𝐴 | |. If the resistance of the loop is R, then the current induced in the
𝑑𝑡
loop is 𝐼𝑖𝑛𝑑 =
ℰ
𝑅
1
𝑑𝐼
𝑅
𝑑𝑡
= 𝜇0 𝑛𝐴 | |.
 What is the force that is causing the charged particles in the conductor to
move? The loop is not moving, so v = 0 for the charged particles in it. But
even if it were moving, it is in a region where B = 0. Therefore the magnetic
⃗ = 𝑞𝒗
⃗ ) cannot be responsible for the motion of charged
⃗ × ⃗𝑩
force (𝑭
particles in the wire loop. The only field we know of that does exert a force
on a stationary electric charge is the electric field, therefore there must be an





induced electric field created by the changing magnetic flux. Remember
⃗⃗ + 𝒗
⃗ ). Here,
⃗ × ⃗𝑩
that, in general, the electromagnetic force is ⃗𝑭 = 𝑞(𝑬
⃗⃗ 𝑖𝑛𝑑 .
⃗ = 0, so ⃗𝑭 = 𝑞𝑬
𝒗
This induced field has the same effect on a charge as the electric fields we
have considered thus far, but the field itself is quite different. It originates as
the result of a changing magnetic flux and is not due to the presence of some
source charge distribution.
The electrostatic field due to a stationary distribution of charge is a
conservative field. One property common to all conservative vector fields is
that a closed line integral of the field will always equal zero. In this case,
⃗ ⋅ 𝑑𝒍 = 0.
∮ ⃗𝑬
The induced electric field, which is created by a changing magnetic flux, is
NOT a conservative field – the line integral of this field around a closed
path is not zero and the concept of potential/potential energy has no
meaning. In fact, this line integral physically represents the work per unit
charge done by the induced field and therefore is equal to the induced emf:
⃗ 𝑖𝑛𝑑 ⋅ 𝑑𝒍 = ℰ
∮ ⃗𝑬
An induced electric field is the result of a changing magnetic flux, regardless
of whether a circuit is present or not. If a circuit is present, then this induced
field can drive a current. However, if we place a single charged particle in
this electric field, it too will experience an electric force. Therefore, it is the
induced field, not the induced emf or current, which is fundamental.
So, for a stationary conductor, Faraday’s law can be restated as:
⃗ 𝑖𝑛𝑑 ⋅ 𝑑𝒍 = − 𝑑Φ𝐵 = ℰ.
∮ ⃗𝑬
𝑑𝑡
𝑑Φ
⃗⃗ ) ⋅ 𝑑𝒍 = − 𝐵 = ℰ is often more
⃗ ×𝑩
 For a moving conductor, ∮(𝒗
𝑑𝑡
convenient. The integration path is usually taken to be along the conductor,
however Faraday’s law as stated in terms of an induced field rather than an
induced emf is true for any closed path (and, as always, that closed path
defines the boundary of the surface chosen for calculating the magnetic
flux).
 Figure (b) (2 pages earlier) shows the view of Figure (a) from the left end.
The current is increasing, so the magnetic flux is increasing into the page.
RHR for induced current: Point your thumb in the direction opposite to the
change in flux and your fingers curl in the direction of the induced current
(CCW).
 As always, we use conventional current so the moving charges are taken to
be positive. This means the induced electric field in the conducting loop is in
the same direction as the induced current (see figure).
 Because the current distribution has cylindrical symmetry, the induced
electric field has a constant magnitude along any circular path centered on
the axis of symmetry and its direction is either tangential or radial. If it were
radial, then by applying Gauss’s law we would be forced to conclude there
was some net charge enclosed by the circle, which is not the case. So, the
induced field is everywhere tangent to the circular path.
⃗⃗ 𝑖𝑛𝑑 ⋅ 𝑑𝒍 = ∮ 𝐸𝑖𝑛𝑑 𝑑𝑙 = 𝐸𝑖𝑛𝑑 ∮ 𝑑𝑙 = 𝐸𝑖𝑛𝑑 (2𝜋𝑟) = |𝑑Φ𝐵 | = 𝜇0 𝑛𝐴 |𝑑𝐼 |.
 ∮𝑬
𝑑𝑡
𝑑𝑡
Thus, the magnitude of the induced field for this situation is given by:
𝐸𝑖𝑛𝑑 =
𝜇0 𝑛𝐴 𝑑𝐼
2𝜋𝑟
| |
𝑑𝑡
 Note the similarity between Ampere’s law and Faraday’s law – Ampere’s
law relates the line integral of the magnetic field around a closed loop to the
current passing thru that loop, while Faraday’s law relates the line integral of
the electric field around a closed loop to the rate of change of the magnetic
flux thru that loop. Both give fields that encircle their respective sources
(currents give rise to magnetic fields that encircle them and changing
magnetic fields give rise to induced electric fields that encircle them). The
field lines for both form closed loops (this is never the case for electrostatic
fields – electric fields due to stationary charge distributions)
 So, the main point of this discussion is that a changing magnetic flux
induces an electric field. This might make you wonder whether or not a
changing electric flux can induce a magnetic field. It turns out that it can.
**EXAMPLE #7**
Displacement Current and Maxwell’s Equations
 So if a changing electric flux were to produce a magnetic field, we would
𝑑Φ
𝑑
⃗ ⋅ 𝑑𝑨
⃗⃗
expect there to be a term on the right hand side involving 𝐸 = ∫ ⃗𝑬
𝑑𝑡
𝑑𝑡
 As I pointed out last chapter, Ampere’s law as it currently stands is
incomplete and only applies to steady currents
 Currents are not always steady (meaning they can vary in time) as we saw in
Chapter 26 when we analyzed RC circuits. As more and more charge is put
on the plates of a capacitor, the current gradually decreases to zero as the
capacitor becomes fully charged.
⃗⃗ ⋅ 𝑑𝒍 = 𝜇0 𝐼𝑒𝑛𝑐
 Recall Ampere’s law was introduced in Chapter 28 as: ∮ 𝑩
 It was not emphasized at that point, but the enclosed current is formally
⃗⃗ , where the integral of the current density 𝑱 is over
defined as 𝐼𝑒𝑛𝑐 = ∫ 𝑱 ⋅ 𝑑𝑨
any open surface bounded by the closed loop chosen for calculating the left
⃗ ⋅ 𝑑𝒍
hand side of Ampere’s law, ∮ ⃗𝑩
 In the figure above, the three surfaces (labeled S1, S2, and S3) are all open
surfaces bounded by the same closed loop (labeled Γ). Ampere’s law says
that the enclosed current must be the same regardless of which surface we
⃗ ⋅ 𝑑𝒍, is the
use to calculate it (since the left hand side of Ampere’s law, ∮ ⃗𝑩
same for all 3 cases).
 Now consider the right hand side of Ampere’s law. Thru both S1 and S3, the
⃗⃗ = 𝐼 but thru S2, ∫ 𝑱 ⋅ 𝑑𝑨
⃗⃗ = 0. There is no conductor
surface integral ∫ 𝑱 ⋅ 𝑑𝑨
between the plates so charge accumulates on the plates but does not flow
thru the gap of width d.
 So, for a time-dependent current, Ampere’s law is not well-defined.
However, once the RC circuit reaches a steady state, the current is
everywhere zero. For a steady current, there is no ambiguity and the right
hand side of Ampere’s law is zero for any surface.
 I suggested earlier that a changing electric flux can induce a magnetic field.
Between the plates of the charging capacitor in the figure above, there is no
current but there is an electric field that is increasing at a rate proportional to
that of the charge accumulation on the plates. This means that there is a
changing electric flux thru S2 (but not thru S1 or S3).
 Ampere discovered his law in 1823 and Maxwell’s equations were more or
less worked out by the end of the 30s, although the mathematical form was
completely different. Around 1860, Maxwell suggested (with no
experimental evidence) that a changing electric flux should create a
magnetic field. He quantified his idea by adding a second term to the right
⃗ ⋅ 𝑑𝒍 = 𝜇0 𝐼𝑒𝑛𝑐 + 𝜇0 𝜀0 𝑑Φ𝐸
hand side of Ampere’s law: ∮ ⃗𝑩
𝑑𝑡
 With this correction, there is no longer any ambiguity in Ampere’s law
applied to the charging capacitor we considered earlier. Thru surface 2, there
is no current and the right hand side is just 𝜇0 𝜀0
𝑑Φ𝐸
𝑑𝑡
. For time-dependent
quantities in a circuit, the book uses lowercase variables: i, v, q. Let’s
assume that we have a parallel-plate capacitor, so the electric field is
spatially uniform between the plates and the potential difference is v = Ed.
𝜀 𝐴
By the definition of capacitance, 𝑞 = 𝐶𝑣 = 0 (𝐸𝑑) = 𝜀0 𝐸𝐴 = 𝜀0 Φ𝐸
𝑑
 If we consider the time derivative of this equation, we have
𝑑𝑞
𝑑𝑡
= 𝜀0
𝑑Φ𝐸
𝑑𝑡
which is, by definition, also the current in the conducting wire that makes up
the circuit. So even though there is no physical movement of charge between
the capacitor plates, the changing electric flux has the same effect as an
actual current in generating a magnetic field. This “current” is often called
the displacement current. And even though we used the specific case of a
parallel-plate capacitor, this is a fundamental aspect of nature – any
changing electric flux results in an induced magnetic field.
 For a circular parallel-plate capacitor, if one measures the magnetic field
directly above where there is no wire but outside of the plates, it behaves
exactly how it would, if there were no capacitor and the wire were
continuous. So the displacement current is a real effect and not just a
mathematical construct.
MAXWELL’S EQUATIONS
⃗⃗ = 𝑄𝑒𝑛𝑐
∮ ⃗𝑬 ⋅ 𝑑𝑨
𝜀
0
⃗ ⋅ 𝑑𝑨
⃗ =0
∮ ⃗𝑩
⃗ ⋅ 𝑑𝒍 = −
∮ ⃗𝑬
𝑑Φ𝐵
𝑑𝑡
⃗ ⋅ 𝑑𝒍 = 𝜇0 𝐼𝑒𝑛𝑐 + 𝜇0 𝜀0
∮ ⃗𝑩
𝑑Φ𝐸
𝑑𝑡
⃗⃗ + 𝒗
⃗ ), these equations describe all classical
⃗ × ⃗𝑩
 Along with ⃗𝑭 = 𝑞(𝑬
electromagnetic phenomena. In addition, they predict and describe the
behavior of electromagnetic waves, and unlike what we’ve studied so far,
their description depends crucially on Maxwell’s modification of Ampere’s
law: 𝜇0 𝜀0
𝑑Φ𝐸
𝑑𝑡
. The simplest description of their behavior is when they are
propagating thru empty space (a vacuum).
 In a vacuum, there are no physical charges nor currents (𝑄𝑒𝑛𝑐 = 0 and
𝐼𝑒𝑛𝑐 = 0) so the electric and magnetic fields in Maxwell’s equations are on
equal mathematical footing. Thus, the only source of either field is a change
in the other field. Faraday’s law says that a changing magnetic field induces
an electric field. Ampere’s law says that a changing electric field induces a
magnetic field. And so, in a vacuum…
𝑑Φ𝐵
⃗ ⋅ 𝑑𝑨
⃗⃗ = 0
∮𝑬
⃗⃗ ⋅ 𝑑𝒍 = −
∮𝑬
⃗ ⋅ 𝑑𝑨
⃗ =0
∮ ⃗𝑩
⃗ ⋅ 𝑑𝒍 = 𝜇0 𝜀0
∮ ⃗𝑩
𝑑𝑡
𝑑Φ𝐸
𝑑𝑡