Download Raman spectroscopy

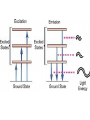
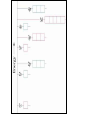
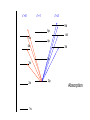
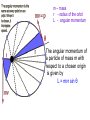
Raman spectroscopy
• You are already aware that photons interact
with molecules to induce transitions between
energy states.
• In Raman spectroscopy- a photon is scattered
by the molecular system.
Raleigh Scatter (same wavelength as incident light)
Raman Scatter (new wavelength)
• Elastic, or Raleigh scattering : the photon simply 'bounces' off
the molecule, with no exchange in energy.
• Inelastic, or Raman scattering: there is an exchange of
energy between the photon and the molecule, leading to the
emission of another photon with a different frequency to the
incident photon
2
• Raman scattering can occur with a change in
vibrational, rotational or electronic energy of a
molecule.
• Chemists are concerned primarily with the
vibrational Raman effect.
The Raman effect arises when a photon is incident on a
molecule and interacts with the electric dipole of the molecule.
This interaction can be viewed as a perturbation of the
molecule’s electric field
- Energy level diagram for Raman scattering
- scattered photon have (a) lower energy
(b) higher energy
than the exciting photon
The different possibilities of visual light scattering:
Rayleigh scattering
Stokes scattering (molecule absorbs energy)
and anti-Stokes scattering (molecule loses energy)
• For Raman scattering to occur, the polarizability of the molecule
must vary with its orientation.
• One of the strengths of Raman spectroscopy is that this will be
true for both heteronuclear and homonuclear diatomic
molecules.
• Homonuclear diatomic molecules do not possess a permanent
electric dipole, and so are undetectable by other methods such
as infrared.
• The polarizabilities of these two homonuclear diatomic
molecules will be different.
• Polarizability is the relative tendency of the electron cloud of an atom
to be distorted from its normal shape by the presence of a nearby ion
or dipole : that is, by an external electric field
EXAMPLE: RAMAN SPECTRUM OF CCl4
COMPARISON BETWEEN IR AND RAMAN
SPECTROSCOPIES
IR
Absorption
RAMAN
Scattering
Requires change in
Dipole moment
Requires change in
polarizability.
Aqueous samples difficult
To examine
Aqueous samples
readily examined.
Glass or quartz unsuitable
As IR cells. NaCl, KBr,
CaF2 are suitable.
Glass or quartz suitable
Electronic spectroscopy
Electronic energy levels of a molecule gives much more
information about the structure of molecules
• Atomic spectrum
•
•
•
- consists of series of lines or
sharply defined emission or
adsorption peaks
•
•
•
•
- because, in the vapour phase
they can neither vibrate or rotate
and have few collisions with each
other
V or λ
• Electrons can get into the excited states by either colliding with
other atoms or absorbing photons of specific energies.
• Absorption Lines:
• - Can be observed when an electron absorbs a photon with
exactly the energy needed to jump from a lower to a higher
orbital.
Absorption is very specific:Only photons with the exact
excitation energy are absorbed.
- All others pass through
unabsorbed.
A continuous spectrum from the
lamp crossed by of dark
"absorption lines" at particular
wavelengths
• Emission Lines:
• When an electron jumps from a higher to a lower energy
orbital, a single photon is emitted with exactly the energy
difference between orbitals. No more, no less.
• Emits only at particular wavelengths, giving the
appearance of bright, discrete "emission lines" Darkness in
between the emission lines
• Comparison of the emission and absorption
lines of sodium
• Each element have a characteristic line spectrum.
• - It is a reflection of the detailed structure of the atom.
Depends on the number and arrangement of electrons in orbit
around the nucleus.
• The Spectral Lines are a kind of "signature" for the atoms.
• The spectra of molecules are quite different from those of the
atom
Hydrogen spectra from
(a) molecular hydrogen (H2) and
(b) atomic hydrogen
•
•
•
•
•
Atomic orbital and their energies
An atomic orbital is a one electron wave function
Each hydrogenic atom is defined by 3 quantum numbers
Principle quantum number
n = 1, 2, 3,…………
Angular momentum quantum number l = 0, 1, 2, 3, …………
Magnetic quantum number m l = 0, ±1, ± 2, ± 3, …………
• A electron in an orbital with quantum number n has an energy
me e 4
hcRH
En 
 2
2 2 2
n
8 0 h n
•
•
•
•
•
•
Me- mass of an electron
E - charge of an electron
ε0- vacuum permittivity
n – principal quantum number
h – Plank’s constant
RH – Rydberg constant
• Principal quantum number
• n
1 2 3 4………..
•
K L M N …………
• Sub cells are given by
•
•
l =0 1 2 3 4
s p d f g
5 6 …………
h i ……..
• The orbitals with same value of n, but different values of l are
said to form a sub-shell of a given shell
• Hydrogen: The Simplest Atom
An atom of Hydrogen (1H) consists of:
- A single proton in the nucleus.
- A single electron orbiting the
nucleus.
First orbital: Ground State (n=1)
Lowest energy orbital the electron
can reside in.
Higher orbitals: Excited States (n=2,3,...)
- Higher orbits around the nucleus.
- Come at specific, exact energies.
• Selection rules which govern the transition of electron between
energy levels of hydrogenic atoms (He+, Li2+ , Be3+ and , B4+ )
• 1. Δn any value
• 2. An s electron can not make any transition to another s orbital
• 3. Electron in a d orbital (l =2) can not make a transition to an s
•
orbital (l =0)
• Therefore the derived selection rules for hydrogenic atoms are:
•
Δn any value , s
s
•
Δl = ±1
•
eg.
l =1 (p)
•
l =2 (d)
l =0 (s)
• Therefore an electron in the ground state (1s) can undergo any
transition to any p state
•
1s
np (n≥ 2)
•
2p
ns or nd
l =0
l =1
l =2
5d
5p
5s
4d
4p
4s
3d
3p
3s
2s
Forbidden
2p
Allowed
transition
transition
1s
Absorption
l =0
l =1
l =2
5d
5p
5s
4d
4p
4s
3d
3p
3s
2s
1s
2p
Absorption
l =0
l =1
l =3
l =2
5f
5d
4f
5p
5s
4d
4p
4s
3d
3p
3s
2s
1s
2p
Absorption
l =0
l =1
Paschen
series
l =2
5d
5p
4d
5s
4p
4s
3d
3p
3s
Balmer
series
2p
2s
1s
Emission
Lyman
series
How other quantum numbers beside n affect the electronic
energy levels?
• Orbital angular momentum(l )
• Electrons are rotating around its nucleus creating orbital
angular momentum
• This momentum is quantized
h
l  l (l  1) .
2
• l – is the orbital angular momentum quantum number
l = 0, 1, 2, 3, …………
m – mass
r - radius of the orbit
L - angular momentum
The angular momentum of
a particle of mass m with
respect to a chosen origin
is given by
L = mvr sin θ
• Electron spin angular momentum (S)
• Every electron in an atom can spin about its own axis
as well as rotate around the nucleolus.
• The spin motion can be expressed by the following
expression
h
s  s ( s  1) .
2
•
•
•
s– is the spin angular momentum quantum number
and it is a half-integral for a one electron atom (±1/2)
• Total electronic angular momentum
j  l s
• Spin orbital coupling
• An electron has a spin angular momentum and it also has a
magnetic momentum that arises from its spin
• ( a moving charge generates a magnetic field)
• Electron with orbital angular momentum creates a circulating
current and possesses a magnetic moment that arises form its
orbital momentum
• The interaction of spin & orbital magnetic moments is called
spin-orbital coupling
• Energy levels are split as a result of spin-orbital coupling
• (j –splitting)
• Total electronic angular momentum
j  l s
• When l =1 (p electron) s = ±1/2
•
•
•
•
•
- therefore j = 3 ∕ 2 or 1 ∕ 2
- the p state is split into two energy states
l =2 (d electron) s = ±1/2
- therefore j = 5 ∕ 2 or 3 ∕ 2
- the d state is split into two energy states
Energy
3d
3p
3/2
1/2
3s
2p
2s
1s
1/2
5/2
3/2
3/2
1/2
* s = -1/2 is not allowed,
since a quantum number
can not be negative
• Selection rules
•
Δn any value
•
Δ l = ±1
•
Δ j = 0, ±1
• Therefore allowed transition between s and p levels are
•
s1/2
p1/2 (Δ j = 0)
•
s1/2
p3/2 (Δ j = +1)
• Every line in the H-spectrum is split into two as a result of
• j-splitting
•
-gives doublets
•
-the separation between lines are too small to be
•
resolved
• The inclusion of coupling between orbitals and spin momentum
has sligtly increased the complexicity of H-spectrum
• The selection rules for the splitting for alkali
metals (Li, Na, K, Rb, Cs) are the same as
hydrogen
•
Δn any value
•
Δ l = ±1
•
Δ j = 0, ±1
• The spiting due to l and s incerases remarkably
with the atomic number
•
H – can not separate
•
Li – less than 1 cm-1
•
Na – 17 cm-1
•
Cs – 500 cm-1