Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Analyzing Isosceles Triangles
Document related concepts
Tessellation wikipedia , lookup
Noether's theorem wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Multilateration wikipedia , lookup
Golden ratio wikipedia , lookup
Apollonian network wikipedia , lookup
Four color theorem wikipedia , lookup
Euler angles wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Rational trigonometry wikipedia , lookup
History of trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
Euclidean geometry wikipedia , lookup
Transcript
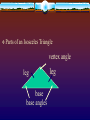
The Isosceles Triangles Theorems Section 4-6 Isosceles Triangle Theorem If 2 sides of a triangle are congruent, then the angles opposite those sides are congruent. 8 8 50 50 Theorem 4-10 If 2 angles of a triangle are congruent, then the sides opposite those angles are congruent. Corollaries 4.3 and 4.4 A triangle is equilateral if and only if it is equiangular. Each angle of an equilateral triangle measures 60 degrees. 12 60 12 60 60 12 Parts of an Isosceles Triangle vertex angle leg base base angles leg The bisector of the vertex angle of an isosceles triangle is perpendicular to the base at its midpoint. Joke Time Who was the first math student? Add-em Why isn’t your nose 12 inches long? Because then it would be a foot
