* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Applied Geometry
Tessellation wikipedia , lookup
Multilateration wikipedia , lookup
Steinitz's theorem wikipedia , lookup
Golden ratio wikipedia , lookup
History of geometry wikipedia , lookup
Euler angles wikipedia , lookup
Noether's theorem wikipedia , lookup
Riemann–Roch theorem wikipedia , lookup
Brouwer fixed-point theorem wikipedia , lookup
Four color theorem wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Incircle and excircles of a triangle wikipedia , lookup
Euclidean geometry wikipedia , lookup
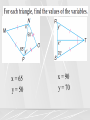
Applied Geometry Lesson: 6 – 4 Isosceles Triangles Objective: Learn to identify and use properties of isosceles triangles. Parts of an Isosceles Triangle Isosceles Triangle Theorem If two sides of a triangle are congruent, then the angles opposite the sides are congruent. Theorem 6-3 The median from the vertex angle of an isosceles triangle lies on the perpendicular bisector of the base and the angle bisector of the vertex angle. x = 49 y = 90 Because EG is also a perpendicular bisector. x = 65 y = 50 x = 90 y = 70 Converse of Isosceles Triangle Theorem If two angles of a triangle are congruent, then the sides opposite those angles are congruent. mB 48 mA mB mC 180 48 48 mC 180 mC 84 4x = 6x - 5 AC = 4(2.5) = 10 -2x = -5 x = 2.5 BC = 6(2.5) -5 = 10 mC 84 AC 10 BC 10 Theorem 6-5 A triangle is equilateral if and only if it is equiangular. Homework Pg. 249 1 – 5 all, 6 – 22 E