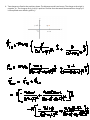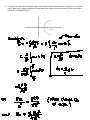Download 1. In the Bohr theory of the hydrogen atom, an electron moves in a

Name(Last, First):______________________________,___________________ RuID#:__ __ __ __ __ __ __ __ __
1. In the Bohr theory of the hydrogen atom, an electron moves in a circular orbit about a proton. The radius
of the orbit is 0.53 x 10-10 m.
a) Find the electric force between the two.
b) Assuming that only this force is present, what is the speed of the electron?
2. A) Determine the electric potential at point P for a ring of
radius R that has a uniformly distributed charge Q.
B) Determine the electric field at point P.
3. An insulating solid sphere of radius “a” has a uniform volume charge density ρ and carries a total charge Q.
A) Calculate the magnitude of the electric field at a point outside the sphere (r > a).
B) Find the magnitude of the electric field at appoint inside the sphere (r < a).
4. Two charges are fixed at the positions shown. The distances a and b are known. The charge at the origin is
negative, -q1. The charge q2 at (x,y)=(a,b) is positive. Find the force that would be exerted on a charge q 3 if
it were placed at an arbitrary point x,y.
5. A charge Q is uniformly distributed along a semicircle of radius R whose center is a distance “a” from the
origin. What point charge would have to be placed at the origin so that the electric field at the center of
the semi-circle would be zero?
6. A solid copper sphere has been given a charge Q. The sphere has a radius R. The electric field is measured
and found to be zero inside the sphere (conducting sphere) and given by |𝐸⃑ | = 𝑘𝑄/𝑟 2 outside of the
sphere (r is the distance from the center of the sphere, the direction of 𝐸⃑ is radially out).
Find the difference in the electric potential between a point a distance 3R from the center of the sphere
and a point at the center.
7. Consider a cubical surface of side L. The bottom is in line with the x,z plane and the back corner is at x=B.
There is an electric field present given by: 𝐸⃑ = 𝐴𝑥𝑖̂ + 𝐵𝑦 2 𝑗̂ + 𝐶𝑥𝑘̂ (A, B, C are known constants.
a) Find the electric flux through the front y-z surface (horizontal dotted lines).
b) Find the electric flux through the front x-z plane (vertical dotted lines).