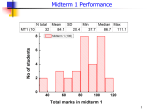
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Basic Electronics
History of electric power transmission wikipedia , lookup
Electrical ballast wikipedia , lookup
Stepper motor wikipedia , lookup
Mercury-arc valve wikipedia , lookup
Voltage optimisation wikipedia , lookup
Electrical substation wikipedia , lookup
Stray voltage wikipedia , lookup
Mains electricity wikipedia , lookup
Thermal runaway wikipedia , lookup
Voltage regulator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Two-port network wikipedia , lookup
History of the transistor wikipedia , lookup
Alternating current wikipedia , lookup
Surge protector wikipedia , lookup
Current source wikipedia , lookup
Power MOSFET wikipedia , lookup
Buck converter wikipedia , lookup
Rectiverter wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
Basic Electronics Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur Lecture : 1 Junction Diode Characteristics Open Circuited p-n Junction In Equilibrium (no bias) Total current balances due to the sum of the individual components no net current! Electron Drift Current Hole Diffusion Current Electron Diffusion Current Hole Drift Current Open Circuited p-n Junction In Equilibrium (no bias) Total current balances due to the sum of the individual components n vs. E n-Type Material - qVBI p-Type Material EC ++ Ei EF EV + + + + + + + + + + + + + + + + + EC EF Ei EV p vs. E Jn Jn Drift Jn Diffusion q n nE q Dn n 0 Jp Jp Drift Jp Diffusion q p pE q D p p 0 no net current! PN Junction I-V Characteristics Forward Bias (VA > 0) IN Electron Drift Current Lowering of potential hill by VA Electron Diffusion Current Current flow is proportional to e(Va/Vref) due to the exponential decay of carriers into the majority carrier bands VA Hole Diffusion Current Current flow is dominated by majority carriers flowing across the junction and becoming minority carriers I IP Hole Drift Current I IN IP PN Junction I-V Characteristics Reverse Bias (VA < 0) Electron Drift Current Current flow is constant due to thermally generated carriers swept out by E fields in the depletion region Increase of potential hill by VA Electron Diffusion Current negligible due to large energy barrier Hole Diffusion Current negligible due to large energy barrier Current flow is dominated by minority carriers flowing across the junction and becoming majority carriers Hole Drift Current PN Junction I-V Characteristics Where does the Reverse Bias Current come from? Generation near the depletion region edges “replenishes” the current source. PN Junction I-V Characteristics Putting it all together -I0 for Ideal diode Vref = kT/q Current-Voltage Characteristics of a Typical Silicon PN Junction Diode Equation qV 1 I I 0 exp kT Lecture : 2 Current Components in a P-N Diode Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur Current Components in a P-N Diode Quisineutral Region Quisineutral Region x”=0 x’=0 Total on current is constant throughout the device. Thus, we can characterize the current flow components as… J -xp xn Current Components in a P-N Diode PN -junction diode structure used in the discussion of currents. The sketc h shows the dimensions and the bias convention. The cross-sectional area A is assumed to be uniform. Current Components in a P-N Diode Hole current (solid line) and recombining electron current (dashed line) in the quasi-neutral n-region of the long-base diode of Figure 5.5. The sum of the two currents J (dot-dash line) is constant. Current Components in a P-N Diode Hole density in the quasi-neutral n-region of an ideal short base diode under forward bias of Va volts. Current Components in a P-N Diode The ratio of generation region width Xi to space charge region width Xd as a function of reverse voltage for several donor concentrations in a one-sided step junction. Current Components in a P-N Diode The current components in the quasi-neutral regions of a long-base diode under moderate forward bias: J(1) injected minority-carrier current, J(2) majority-carrier current recombining with J(1), J(3) majority-carrier current injected across the junction. J(4) space-charge-region recombination current. Current Components in a P-N Diode J p-region SCL n-region J = J elec + J hole Total current Majority carrier diffusion and drift current J h ole J elec Minority carrier diffusion current x –Wp Wn The total current anywhere in the device is constant. Just outside the depletion region it is due to the diffusion of minority carriers. Lecture : 3 Breakdown Diodes and Temperature Effect on Diode Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur Breakdown Diodes When the reverse voltage applied across diode becomes greater than the breakdown voltage, then the diode breaks down and very high current starts flowing in the circuit. There are generally two types of breakdowns in a diode: 1. Zener breakdown 2. Avalanche breakdown And based on the above classifications of breakdown of diode, we have the two special types of diode as 1. Zener breakdown 2. Avalanche breakdown The difference between the Zener Diode and avalanche Diode is the doping level. The doping level of Zener diode is more than avalanche diode or we can say diodes which have higher doping level undergo Zener breakdown when reverse bias voltage is increased while diodes with lesser doping level undergo Avalanche breakdown. Breakdown Diodes Zener diode : As we have already mentioned doping level of Zener diode is very high and hence width of depletion region is less. As we know E = VB / d VB is the barrier voltage E is the electric field d is the depletion width As doping is high, hence width (d) is less and as barrier voltage varies with doping as stated by the formula: From the formula we can get that the voltage varies proportional to log of doping and hence the barrier voltage is almost constant. So from the above discuss we find that Electric field in the depletion region would be large as VB is almost constant and d has decreased. Due to this large electric field, electrons from the outer shell of the atom in the depletion region are expelled out and hence carriers are generated within the depletion region. The high electric field in the depletion region pulls out large number of electrons from the large number of atoms. This leads to large current flow and this type of breakdown is called Zener breakdown. Breakdown Diodes Avalanche diode : The diode which have lesser doping undergo avalanche breakdown when high reverse voltage is applied. The lesser doping means the depletion width is large and so electric field within depletion region is not so high. Hence the electric field would not be able to pull out electrons from the outer shell of atoms and breakdown doesn’t occur in depletion region. But as the depletion region is large and hence when the minority charge carriers move through the depletion region, they get accelerated by the electric field and that even for larger time (as distance through which acceleration is provided is large). Hence minority charge carriers acquire high velocity and so high kinetic energy. When these charge carriers strike with atoms in the n-type and p-type regions, the high kinetic energy gets converted to thermal energy and hence due to this energy electrons from the outermost shell are pulled out and large current starts flowing. This type of breakdown is called avalanche breakdown. But due to the high thermal energy, the temperature rises and diode gets burned. Due to this reason the simple diodes (where avalanche breakdown occurs) is not used in th e applications and instead Zener diode is used in the application circuits of breakdown diodes such as regulating power supply. Breakdown Diodes Differences between Zener breakdown and Avalanche breakdown: Zener breakdown 1. The Zener breakdown occurs in HIGH doping diodes. 2. The breakdown occurs within the depletion region. 3. The breakdown voltage is lesser than zener that of avalanche breakdown. Avalanche breakdown 1. The avalanche breakdown occurs in LOW doping diodes. 2. The breakdown occurs outside the depletion region. 3. The breakdown voltage is more than breakdown voltage. As Zener breakdown voltage is less than that of avalanche breakdown voltage, hence Zener breakdown is said to occur before the avalanche breakdown. Hence we can say if we increase the doping of a diode, the chances of zener breakdo wn increases and hence breakdown voltage decreases. Temperature Effect on Diode The following graph shows the effect of temperature on the characteristics of diode A-B curve: This curve shows the characteristics of diode for different temperatures in the forward biase. As we can see from the figure given above, that curve moves towards left as we increase the temperature. We know with increase in temperature, conductivity of semiconductors increase. The intrinsic concentration (ni) of the semiconductors is dependent on temperature as given by: Eg is the energy gap K is a voltage man constant A is a constant independent of temperature Temperature Effect on Diode When temperature is high, the electrons of the outermost shell take the thermal energy and become free. So conductivity increases with temperature. Hence with increase in temperature, the A-B curve would shift towards left i.e. curve would rise sharply and the breakdown voltage would also decrease with increase in temperature. A-C curve: This curve shows the characteristics of diode in the reverse biased region till the breakdown voltage for different temperatures. We know ni concentration would increase with increase in temperature and hence minority charges would increa se with increase in temperature. The minority charge carriers are also known as therm ally generated carriers and the reverse current depends on minority carriers only. Hence as the number of minority charge carriers increase, the reverse current would also increase with temperature as shown in the figure given on the previous page. The reverse saturation current gets double with every 10 C increase in temperature. C-D curve: This curve shows the characteristics of a diode in reverse biased region from the breakdown voltage point onwards. As with increase in temperature, loosely bonded electrons are already free and to free the other electrons, it would take more voltage than earlier. Lecture : 4 Junction Diode Switching Times Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur. Junction Diode Switching Times The switching time of a diode is defined as the time which a diode takes to change its state from forward biased state to reverse biased state or in other words the forward current through diode doesn’t reduce to reverse saturation current immediately as the reverse voltage is applied. In fact it takes time for the current to reduce from forward current to reverse saturation current. This time is also called reverse recovery time. To discuss more about the switching time, we first need to discuss charge distribution of diode in normal state, forward biased state and reverse biased state assuming doping of p-type is more than n-type. Apply the relation given below n * p = ni2 at constant temperature (Mass action law) Junction Diode Switching Times Now we apply the above relation to p-type : P i.e. the concentration of majority carriers (holes) is larger as doping of p-side is high and we have the value of ni2 as constant at fixed temperature. Hence from the above relation we find that number of minority carriers (electrons) is less in p-type material while as doping of n-side is normal, hence number of majority carriers (i.e. electrons) in n-side is not large with the value of ni2as constant and hence number of minority carriers is larger as compared to that in p-side. Npo is defined as the concentration of minority carriers in N-type material i.e. holes and Pno is defined as the concentration of minority carriers in P-type material i.e. electrons when diode is in un-biased. Junction Diode Switching Times Charge distribution of diode in Forward Biased state : When diode is forward biased, the majority carriers of both sides cross the junction and after reaching the other side, the charge carriers start combining. So holes from p-side start moving towards n-side and electrons from n-side start moving to p-side. When holes enter the n-side they become the minority carriers and just at the junction there would be high concentration of holes in n-side as the recombining has just started. Also all the holes can not recombine at the junction. Hence when we move away from the junction in the n-side, the concentration of holes is decreasing as more and more holes are recombining. This is also shown in the figure below. Similarly in the p-side, concentration of the electrons is high near the junction and it starts decreasing as we move away from the junction in the p-side. Junction Diode Switching Times Charge distribution of diode in Reverse Biased state : When we reverse biased any diode, the minority carriers from both sides cross the junction and then recombine after reaching the other side. Hence the holes from n-side move towards p-side and after reaching p-type material become majority carriers. These holes combine with minority carriers of p-side i.e. electrons. So the minority carriers at junction i.e. holes in the n-side which are near junction would immediately cross the junction on reverse biased and other holes move slowly. Similar to the above, electrons of p-side move to n-side. Junction Diode Switching Times Diode Reverse Recovery Time : Consider the following circuit of diode to analyze the switching time of diode. So to change state from forward to reverse biase, the whole minority charge distribution needs to be inverted as we can see from the figures above. Junction Diode Switching Times Diode Reverse Recovery Time : Now let’s see what happens during the period in which state changes. Firstly we are in forward biased state when voltage applied is + V. So there are many minority carriers near the junction and then there is an exponential decrease in the concentration of minority carriers and there is a continuous flow of majority carriers across the junction. We assume the current as I in the forward biased. We depict this in the following graph of current across the junction with time. Junction Diode Switching Times Now we change the applied voltage to –V at time t=t1 i.e. diode is now reverse biased. As minority carrier concentration in both sides was large near junction in the forward biased, when we have instantly changed the state to reverse biased, those minority arriers start moving in the opposite direction. And due to large concentration of such minority carriers, the amount of current flowing remains the same. Junction Diode Switching Times But the high reverse current continues for small time because the concentration of the stored minority carriers start decreasing and the current also starts decreasing exponentially as shown below: The time gap t2 - t1 in which the reverse current is high (i.e. equal to I) is known as storage time and the time gap from t2 to t3 i.e. the time reverse current becomes equal to reverse saturation current is known as transient time. The total time from t1 to t3 is known as reverse recovery time. Junction Diode Switching Times Effect Of Doping On Reverse Recovery Time : As we have already known that reverse recovery time is the time it takes to invert the minority charge distribution of diode from forward biased to minority charge distribution in reverse biased. Hence when we increase the doping of material, the concentration for minority charge carriers decrease. Hence as the peaks of charge distribution have fallen, it takes lesser time to invert the charge distribution. Hence we can say that with increase in doping, the reverse recovery time decrease and with decrease in doping level the reverse recovery time increases. Lecture : 5 Transistor Characteristics Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur What is a Transistor? Semiconductors: ability to change from con ductor to insulator Can either allow current or prohibit current to flow Useful as a switch, but also as an amplifier Essential part of many technological advances A Brief History Guglielmo Marconi invents radio in 1895 Problem: For long distance travel, signal must be am plified Lee De Forest improves on Fleming’s original vacuu m tube to amplify signals Made use of third electrode Too bulky for most applications The Transistor is Born Bell Labs (1947): Bardeen, Bratta in, and Shockley Originally made of germanium Current transistors made of doped silicon How Transistors Work Doping: adding small amounts of other elements to create additional protons or electrons. P-Type: dopants lack a fourth valence electron (Boron, Aluminum). N-Type: dopants have an additional (5th) valence electron (Phosphorus, Arsenic). Importance: Current only flows from P to N. Physical Structure of Transistor Diodes and Bias Diode: simple P-N junction. Forward Bias: allows current to flow from P to N. Reverse Bias: no current allowed to flow from N to P. Breakdown Voltage: sufficient N to P voltage of a Zener Diode will allow for current to flow in this direction. The Bipolar Junction Transistor Normally Emitter layer is heavily doped, Base layer is lightly doped and Collector layer has Moderate doping. The Two Types of BJT Transistors PNP NPN n E p n C E p n p B B Cross Section Cross Section C C B B E Schematic Symbol E 109 Collector doping is usually ~ Base doping is slightly higher ~ 1010 – 1011 Emitter doping is much higher ~ 1017 Schematic Symbol C Junction Transistor IE E - VCE + IC - IE - C E + VEC IC - C + VBE IB VBC + VEB - - + + B B NPN : IE = IB + IC VCE = -VBC + VBE PNP : IE = IB + IC VEC = VEB - VCB VCB IB Lecture : 6 Transistor Current Components Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur Transistor Current Components In the figure we show the various components which flow across the forward-based emitter junction and the reverse-biased collector junction. The emitter current IE consists of hole current IpE (holes crossing from the emitter into base) and electron current InE (electron crossing from base into the emitter). The ratio of hole to electron currents, IpE/InE, crossing the emitter junction is proportional to the ratio of the conductivity of the p material to that of the n material. In the commercial transistor the doping of the emitter is made much larger than the do ping of the base. This future ensures (in a p-n-p transistor) that the emitter current consists almost entirely of the holes. Such a situation is desired since the current which results from electrons crossing the emitter junction from base to emitter does not contribute carriers which can reach the collector. Transistor Current Components Not all the holes crossing the emitter junction JE reach the collector junction Jc because some of them combine with the electrons in the n – type base. If Ipc is the hole current at Jc, there must be a bulk recombination current IpE - IpC leaving the base, as indicated in figure. (actually, electrons enter the base region through the base lead to supply those charges which have been lost by recombination with the holes injected into the base across JE). If the emitter were open-circuited so that IE = 0, then IpC would be zero. Under these circumstances, the base and collector would act as a reverse-biased diode, and the collector current Ic would equal the reverse saturation current ICO. If IE ≠ 0, then, from figure, we note that, Ic = Ico – IpC For a p-n-p transistor, Ico consists of holes moving across Jc from left to right (base to collector) and electrons crossing Jc in the opposite direction. Since the assumed reference direction for Ico in figure is from right to left, then for a p-n-p transistor, Ico is negative. For an n-p-n transistor, Ico is positive. Current flow for an NPN BJT in the active region n I co - Inc + VCB - p- Electrons + Holes + VBE - Ipe Ine n+ Bulk-recombinati on Current Most of the current is due to electrons moving from the emitter through base to the collector. Base current consists of holes crossing from the base into the emitter and of holes that recombine with electrons in the base. Current flow for an NPN BJT in the active region For CB Transistor IE= Ine+ Ipe Bulk-recombination current ICO Inc Ic= Inc- Ico And Ic= - αIE + Ico CB Current Gain, α ═ (Ic- Ico) (IE- 0) For CE Transistor, IC = βIb + (1+β) Ico where β ═ α , 1- α is CE Gain. Ipe Ine Lecture : 7 Transistor Configurations Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur Various Regions (Modes) of Operation of BJT Active: Most important mode of operation Central to amplifier operation The region where current curves are practically flat Saturation: Barrier potential of the junctions cancel each other out causing a virtual short (behaves as on state Switch) Cutoff: Current reduced to zero Ideal transistor behaves like an open switch There is also a mode of operation called inverse active mode, but it is rarely used. Three Possible Configurations of BJT Biasing the transistor refers to applying voltages to the transistor to achieve certain operating conditions. 1. Common-Base Configuration (CB) : input = VEB & IE output = VCB & IC 2. Common-Emitter Configuration (CE): input = VBE & IB output= VCE & IC 3. Common-Collector Configuration (CC) :input = VBC & IB (Also known as Emitter follower) output = VEC & IE Common-Emitter BJT Configuration Region of Operation Description Active Small base current controls a large collector current Saturation VCE(sat) ~ 0.2V, VCE increases with IC Cutoff Achieved by reducing IB to 0, Ideally, IC will also be equal to 0. IC IC VCE Active Region VCC + _ IB Circuit Diagram IB Saturation Region VCE Cutoff Region IB = 0 Collector-Current Curves Common-Emitter BJT Configuration BJT’s have three regions of operation: 1) Active - BJT acts like an amplifier (most common use) 2) Saturation - BJT acts like a short circuit BJT is used as a switch by switching 3) Cutoff - BJT acts like an open circuit between these two regions. IC(mA) Saturation Region IB = 200 A 30 Active Region IB = 150 A 22.5 IB = 100 A 15 B IB = 50 A 7.5 Cutoff Region When analyzing a DC BJT circuit, the BJT is replaced by one of the DC circuit models shown below. C E IB = 0 0 VCE (V) 0 5 10 15 20 DC Models for a BJT: C rsat B B + _ B Vo Vo b dc IB ICEO b dc IB IB + _ C C + _ RBB Vo E Saturat ion Region Model E Active Region Model #1 E Active Region Model #2 Ro DC b and DC b = Common-emitter current gain = Common-base current gain b = IC IB = IC IE The relationships between the two parameters are: = b b+1 b= 1- and b are sometimes referred to as dc and bdc because the relationships being dealt with in the BJT are DC. Common-Emitter BJT Configuration Output characteristics: NPN BJT (typical) b dc = IC(mA) IB = 200 A 30 Note: The PE review text sometimes uses dc instead of bdc. They are related as follows: IB = 150 A 22.5 IC = h FE IB IB = 100 A 15 dc = IB = 50 A 7.5 IB = 0 0 0 5 10 15 20 VCE (V) b dc b dc + 1 b dc dc 1 - dc Find the approximate values of bdc and adc from the graph. Input characteristics: NPN BJT (typical) IB(A) VCE = 0.5 V 200 VCE = 0 VCE > 1 V 150 100 50 The input characteristics look like the characteristics of a forward-biased diode. Note that VBE varies only slightly, so we often ignore these characteristics and assume: Common approximation: VBE = Vo = 0.65 to 0.7V Note: Two key specifications for the BJT are Bdc and 0 VBE (V) 0 0.5 1.0 Vo (or assume Vo is about 0.7 V) Common-Emitter BJT Configuration Figure: Common-emitter characteristics displaying exaggerated secondary effects. Common-Emitter BJT Configuration Figure: Common-emitter characteristics displaying exaggerated secondary effects. Common-Base BJT Configuration C The Table Below lists assumptions that can be made for the attributes of the common-base BJT circuit in the different regions of operation. Given for a Silicon NPN transistor. VCE IC VCB IE E VBE + _ + _ IB B VCB Region of Operation IC Active bIB Saturation Max ~0V Cutoff ~0 =VBE+VCE VCE VBE VCB C-B Bias E-B Bias 0V Rev. Fwd. ~0.7V -0.7V<VCE<0 Fwd. Fwd. 0V None/ Rev. VBE =VBE+VCE ~0.7V 0V Rev. Common-Base BJT Configuration Input Characteristics This curve shows the relationship between of input current (IE) to in put voltage (VBE) for various leve ls of output voltage (VCB). Common-Base BJT Configuration Output Characteristic IC mA Breakdown Reg. 6 Saturation Region Active Region 0.8V IE 4 IE=2mA 2 IE=1mA 2V 4V 6V 8V Cutoff IE = 0 VCB Common-Collector BJT Configuration Emitter-Current Curves The Common-Collector biasing circuit is basically equivalent to the common emitter biased circuit except instead of looking a t IC as a function of VCE and IB we are looking at IE. Also, since ~ 1, and = IC/IE that means IC~IE IE Active Regio n IB VCE Saturation Region Cutoff Region IB = 0 Lecture : 8 Ebers-Moll BJT Model Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur. Ebers-Moll BJT Model The Eber-Moll Model for BJTs is fairly complex, but it is valid in all region s of BJT operation. The circuit diagram below shows all the components of the Eber-Moll Model: E IE IC C R IC R IE IF IR IB B Eber-Moll BJT Model R = Common-base current gain (in forward active mode) F = Common-base current gain (in inverse active mode) IES = Reverse-Saturation Current of B-E Junction ICS = Reverse-Saturation Current of B-C Junction IC = FIF – IR IE = IF - RIR IB = I E - IC IF = IES [exp(qVBE/kT) – 1] IR = IC [exp (qVBC/kT) – 1] If IES & ICS are not given, they can be determined using various BJT parameters. Small Signal BJT Equivalent Circuit The small-signal model can be used when the BJT is in the active region. The small -signal active-region model for a CB circuit is shown below: iB iC B biB r r = (b + 1) * VT IE @ = 1 and T = 25C r = (b + 1) * 0.026 IE iE E Recall: b = IC / IB C The Early Effect (Early Voltage) Note: Common-Emitter Configuration IC IB -VA VCE Green = Ideal IC Orange = Actual IC (IC’) Early Effect Example Given: The common-emitter circuit below with IB = 25A, VCC = 15V, b = 100 and VA = 80. Find: a) The ideal collector current b) The actual collector current Circuit Diagram IC VCC b) + _ VCE b = 100 = IC/IB a) IC = 100 * IB = 100 * (25x10-6 A) IC = 2.5 mA IB IC’ = IC VCE + 1 VA IC’ = 2.96 mA = 2.5x10-3 15 + 1 80 = 2.96 mA Lecture : 9 Transistor Biasing Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur. The Thermal Stability of Operating Point SIco The Thermal Stability Factor : Sico SIco = ∂Ic ∂Ico Vbe, β This equation signifies that Ic Changes SIco times as fast as Ico Differentiating the equation of Collector Current IC & rearranging the terms we can write SIco ═ 1+β 1- β (∂Ib/∂IC) It may be noted that Lower is the value of SIco better is the stability The Fixed Bias Circuit 15 V 15 V 200 k RC Rb 1k C B RC The Thermal Stability Factor : SIco SIco = ∂Ic Vbe, β ∂Ico General Equation of SIco Comes out to be SIco ═ 1 + β 1- β (∂Ib/∂IC) Ib E Applying KVL through Base Circuit we can write, Ib Rb+ Vbe= Vcc Diff w. r. t. IC, we get (∂Ib / ∂Ic) = 0 SIco= (1+β) is very large Indicating high un-stability The Collector to Base Bias Circuit VCC RC Ic RF Ib C B +V BE - IE E The General Equation for Thermal Stability Factor, SIco = ∂Ic ∂Ico Vbe, β Comes out to be SIco ═ 1 + β 1- β (∂Ib/∂IC) Applying KVL through base circuit we can write (Ib+ IC) RC + Ib Rb+ Vbe= Vcc Diff. w. r. t. IC we get (∂Ib / ∂Ic) = - RC / (Rb + RC) Therefore, SIco ═ (1+ β) 1+ [βRC/(RC+ Rb)] Which is less than (1+β), signifying better thermal stability The Potential Divider Bias Circuit VCC VCC R1 RC IC C Ib B E R2 RE I C The General Equation for Thermal Stability Factor, SIco ═ 1 + β 1- β (∂Ib/∂IC) Applying KVL through input base circuit we can write IbRTh + IE RE+ Vbe= VTh Therefore, IbRTh + (IC+ Ib) RE+ VBE= VTh Diff. w. r. t. IC & rearranging we get (∂Ib / ∂Ic) = - RE / (RTh + RE) Therefore, 1 b SIco VCC Thevenin Ckt RC IC Ib C B RE 1 b RE RTh This shows that SIco is inversely proportional to RE and It is less than (1+β), signifying better the rmal stability RTh E + _ VTh RE Self-bias Resistor Thevenins Voltage Rth = R1*R2 & Vth = Vcc R2 R1+R2 R1+R2 Potential-Divider Bias Circuit with Emitter Feedback Most popular biasing circuit : Problem: bdc can vary over a wide range for BJT’s (even with the same part number) Solution: Adding the feedback resistor RE. How large should RE be? Let’s see. VCC VCC VCC R1 RC RC C C B B IC = RTh + _ VTh RE b dc VTh - Vo + ICEO R Th + R E R Th + b dc + 1 R E where ICEO = b dc + 1 ICBO E E R2 Substituting the active region model into the circuit to the left and analyzing the circuit yields the following well known equation: RE ICEO has little effect and is often neglected yielding the simpler relationship: Voltage divider biasin g circuit with emitter feedback Replacing the input circuit by a Thevenin equivalent circuit yields: R2 VTh = VCC and R Th = R1 R 2 R + R 1 2 IC = b dc VTh - Vo R Th + b dc + 1 R E Test for stability: For a stable Q-point w.r.t. variations in bdc choose: R Th << bdc + 1 R E Why? Because then IC = b dc VTh - Vo b V - Vo dc Th R Th + b dc + 1 R E b dc + 1 R E VTh - Vo (independent of b dc ) RE Lecture : 10 Transistor at Low Frequencies Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur. A Practical C E Amplifier Circuit VCC VCC Input Signal Source R1 RC io C Co ii Rs + vs + Ci + B E vi _ R2 RE _ Common Emitter (CE) Amplifier RL CE vo _ Graphical Analysis of the CE configuration, If changes in operating currents and voltages are small enough, then IC and VCE waveforms are u ndistorted replicas of the input signal. A small voltage change at the base causes a large voltage change at the collector. The voltage gain is given by: An 8 mV peak change in vBE gives a 5 mA change in iB and a 0.5 mA change in iC. The 0.5 mA change in iC gives a 1.65 V change in vCE . ~ ~ vce 1.65180 Av ~ 206180 206 v 0.0080 be The minus sign indicates a 1800 phase shift between input and ou tput signals. BJT Amplifier using Coupling and Bypass Capacitors In a practical amplifier design, C1 and C3 are large coupling capacitors or dc blocking capacitors, their reactance (XC = |ZC| = 1/wC) at signal frequency is negligible. They are fective open circuits for the circuit when DC bias is considered. C2 is a bypass capacitor. It provides a low impedance path for ac current from emitter to ground. It effectively removes RE (required for good Q-point stability) from the circuit when ac signals are considered. AC coupling through capacitors is used to inject an ac input signal and extract the ac output signal without disturbing the DC Q-point Capacitors provide negligible impedance at frequencies of interest and provide open circuits at dc. Lecture : 11 AC analysis of BJT Amplifier Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur. D C Equivalent for the BJT Amplifier (Step1) DC Equivalent Circuit All capacitors in the original amplifier circuit are replaced by open circuits, disconnecting vI, RI, and R3 from the circuit and leaving RE intact. The the transistor Q will be replaced by its DC model. A C Equivalent for the BJT Amplifier (Step 2) R1IIR2=RB Ro Rin Coupling capacitor CC and Emitter bypass capacitor CE are replaced by short circuits. DC voltage supply is replaced with short circuits, which in this case is conne cted to ground. A C Equivalent for the BJT Amplifier All externally connected capacitors are assumed as short circuited elements for ac signal R R R 10kΩ 30kΩ B 1 2 R R R 4.3kΩ 100kΩ C 3 By combining parallel resistors into equivalent RB and R, the equivalent AC circuit above is constructed. Here, the transistor will be replaced by its equivalent small-signal AC model (to be developed). A C Analysis of CE Amplifier Step 1 1) Determine DC operating point and calculate small signal parameters 2) Draw the AC equivalent circuit of Amp. Step 2 • DC Voltage sources are shorted to ground • DC Current sources are open circuited • Large capacitors are short circuits • Large inductors are open circuits 3) Use a Thevenin circuit (sometimes a Step 3 Norton) where necessary. Ideally the base should be a single resistor + a single source. Do not confuse this with the DC Thevenin you did in step 1. 4) Replace transistor with small signal model Step 4 5) Simplify the circuit as much as necessary. Steps to Analyze a Transistor Amplifier 6) Calculate the small signal parameters and gain etc. Step 5 π-model used Lecture : 12 Hybrid Parameter Model Prof. Rajput Sandeep Assist. Prof., EC Dept. HCET ,Siddhpur. Hybrid-Pi Model for the BJT Transconductance: I gm C ,VT KT q V T Input resistance: Rin b oV bo T r I gm C The hybrid-pi small-signal model is the intrinsic low-frequency representation of the BJT. The small-signal parameters are control led by the Q-point and are independent of the geometry of the BJT. Output resistance: V V ro A CE I C Where, VA is Early Voltage (VA=100V for npn) Hybrid Parameter Model Io Ii Linear Two port Device Vi Vo Ii 1 Vi Io hi hrVo hfIi ho 1' 2 Vo 2' Vi h11Ii h12Vo hi I i hrVo I o h21Ii h22Vo h f I i hoVo h-Parameters Vi h11 Ii Io h21 Ii Vo 0 Vi h12 Vo Ii 0 Vo 0 Io h22 Vo Ii 0 h11 = hi = Input Resistance h12 = hr = Reverse Transfer Voltage Ratio h21 = hf = Forward Transfer Current Ratio h22 = ho = Output Admittance Three Small signal Models of CE Transistor The Mid-frequency small-signal models ib ic c b hie + vbe Alternate names: h fe = b ac = b o = b + hrevce + _ hfe ib hoe vce _ _ e e h-parameter model ib ic + 38.92 IC (Note: Uses DC value of I C ) n where n = 1 (typical, Si BJT) vce b o = h fe rd = h re = 0 r = h ie = c b + + vbe r _ v gmv rd gm = _ _ e e 1 h oe hybrid- model ib ic c b + vbe + bre bib vce _ _ e e re model re = bo gm 26 mV (Note: uses DC value of IB ) IB b o = h fe b o re = h ie h re = 0 h oe = 0, or use rd = 1 h oe BJT Mid-frequency Analysis using the hybrid-p model VCC VCC R1 A common emitter (CE) amplifier RC io The mid-frequency circuit is drawn as follows: the coupling capacitors (Ci and Co) and the bypass capacitor (CE) are short circuits short the DC supply voltage (superposition) replace the BJT with the hybrid-p model The resulting mid-frequency circuit is shown below. C Co ii Rs + + + B Ci E vs vi R2 _ RL RE CE vo _ _ is + vs ii RS vi _ e io c + RTh _ b + r v + gmv ro rd RC Zi An AC Equivalent Circuit e vo Av g m RL' , where, RL' ro RL RC , vi io Ai ii vo _ _ mid-frequency CE amplifier circuit RL Zi v o v o vi Av s Av v s vi v s Z R s i vi RTh r , where, R Th R1 R2 Ii Zo vo io ro RC vi o Small-Signal Analysis for Gain Av (Using Π-model) Rs vo g mv R R ro beC 3 R L Rs From input circuit R ro R R , R L C 3 C R3 vo vo vbe Av v v v i be i vo I o RL g v R m be L v R r i B v be R R r S B R r B Av g m R L R R r B S C-E Amplifier Input Resistance The input resistance, the total resistance looking into the amplifier at coupling capacitor C1, represents the total resistance presented to the AC source. v x i x (R r ) B vx R R r R R r B 1 2 in i x C-E Amplifier Output Resistance The output resistance is the total equivalent resistance looking into the output of the amplifier at coupling capacitor C3. The input source is set to 0 and a test source is applied at the output. v x gm v be R ro C But vbe=0. vx Rout R ro R C C ix ix vx since ro is usually >> RC. An Emitter Follower (CC Amplifier) Amplifier Very high input Resistance Very low out put Resistance Unity Voltage gain with no phase shift High current gain Can be used for impedance matching or a circuit for providing electrical isolation